全双工双向中继系统的功率分配方案

葛 佳, 邱梦婷, 俞 晖

(上海交通大学 电子信息与电气工程学院,上海 200240)

全双工双向中继系统的功率分配方案

葛 佳, 邱梦婷, 俞 晖

(上海交通大学 电子信息与电气工程学院,上海 200240)

提出了最大化系统的频谱效率(SE)和能量效率(EE)两种功率分配方案.EE优化问题用迭代算法求解,首先运用分式规划的方法把优化问题转变成易求解的非分式优化问题,然后运用Dinkelbach算法求得用户节点的最佳功率,再运用一维搜索求得最佳中继放大系数,最后利用迭代算法求得EE最大值.SE优化问题同样用迭代算法求解.仿真结果显示,针对不同目标函数的两种功率分配方案分别提高了系统的EE和SE,同时迭代算法能够快速收敛获得最优解.

频谱效率; 能量效率;全双工;双向中继

0 引 言

无线通信网络日益增长的网络容量需求和传输速率需求给当前频谱资源带来了挑战,而中继技术可以为系统带来更大的容量和覆盖范围,引起了人们广泛的关注.传统的中继节点一般工作在半双工模式,不能同时同频收发信号.半双工模式以牺牲时域或频域为代价,换来的是有限的干扰减少和性能增益,同时造成了频谱资源的浪费.而全双工模式可以同时同频收发信号,一方面,理论上来说,全双工模式的频谱效率(SE)是半双工模式的2倍,大大节约了频谱资源[1-2];另一方面,全双工模式同时同频收发信号会不可避免地给系统带来回路自干扰问题,影响系统的SE和能量效率(EE)[3].虽然当前自干扰消除技术已经较为成熟,自干扰水平已能够控制在合理的范围内[4-5],但是还不能完全消除自干扰,这对SE和EE的优化都会产生影响.因此如何进一步提高系统的SE和EE,对未来的无线通信网络有着重要的意义[5].

目前已有许多文献研究了半双工或全双工场景中针对SE或EE的优化[5-9].文献[5]针对全双工双向中继系统进行了SE-EE的联合优化,忽略了用户产生的自干扰,研究表明当SE大于一定阈值时,EE会随着SE的升高而降低.文献[6]和[7]研究了中继在最大功率发送条件下,单对全双工用户通信时的中继选择,研究表明系统使用全双工双向中继比用全双工单向中继具有更高的SE.文献[8]在半双工单向中继场景中,针对用户发送功率对系统EE进行了优化,并未优化SE.文献[9]考虑了多用户(MU)多进多出(MIMO)的全双工双向中继场景中,中继天线数以及用户对数分别对SE和EE的影响.

本研究假设在完美信道状态信息条件下,考虑了中继及用户节点的自干扰,研究针对不同目标函数的系统功率分配方案.实验仿真结果显示,提出的功率分配方案可以有效提高系统的SE和EE.

1 系统模型

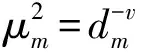
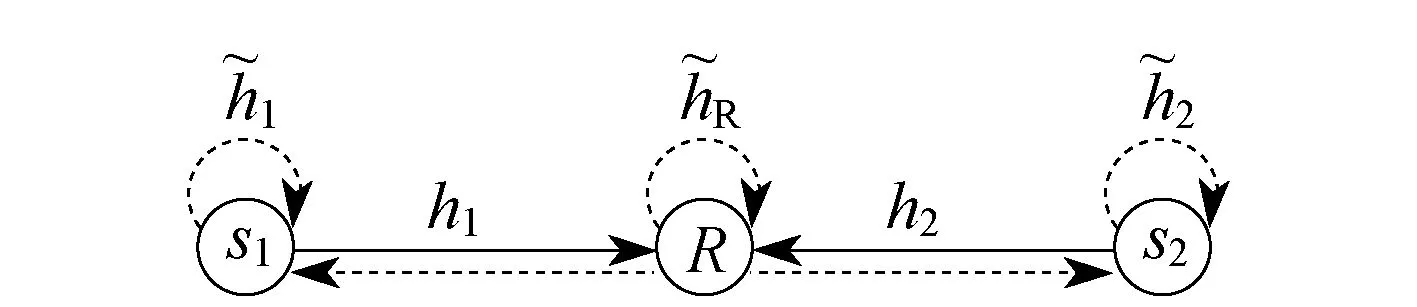
图1 双向全双工中继系统模型

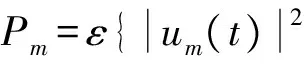
(1)

(2)

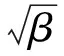
(3)

将(1)带入(3)可以得到

(4)

再将(4)带入(2)可以得到一个包含期望信号、噪声信号和自干扰信号的ym(t)的表达式

(5)

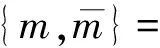
同时由(4)可得中继发送功率的表达式为

(6)

假设(5)右边第四项um(t-d)产生的回路自干扰可以完全消除[10],此时Sm的信号与干扰加噪声比(SINR)可以记为

(7)

故SE表达式为

(8)

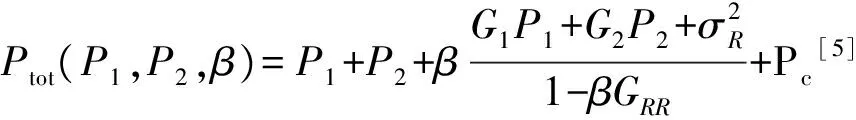
(9)

2 功率分配方案

本节针对不同的目标函数分别采用不同的功率分配方案.

2.1 能效最大化的功率分配方案

求解使得EE最大时的各节点的功率,数学模型如下:

(10)

对于问题(10),目标函数ηEE关于P1,P2和β三元优化变量的凹凸性要通过计算hessian矩阵求得,计算量巨大.为了简化该问题的求解,本文作者采用一种迭代优化的算法来求得ηEE的最大值,具体做法是,首先将β作为定值,P1和P2作为优化变量来优化目标函数,再将优化得到P1和P2作为定值,β作为优化变量来优化目标函数,如此反复迭代优化,直到最后的优化结果趋于收敛,优化完成.

当β为定值时,优化问题(10)变成

(11)

问题(10)的目标函数为关于P1和P2非线性分式函数,凹凸性同样难以判断.为了将该式转化为一个易于判断凹凸性的非分式问题,引入常量q,令FEE(P1,P2)=ηSE-qPtot,将(11)转化为以下等价形式:

(12)

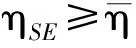
由命题1可知,问题(11)的最优解即为q*.利用Dinkelbach算法迭代求解可以方便地求得q*,计算步骤如下:

步骤一:初始化设定最大循环次数Nmax,q的初始值q1,最大允许误差δ0,循环次数变量i=1;

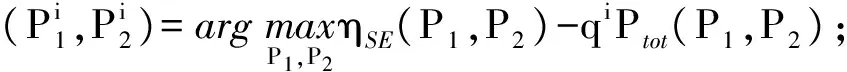
步骤四:计算i=i+1;

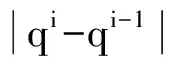
当P1和P2为定值时,优化问题(10)变成

(13)

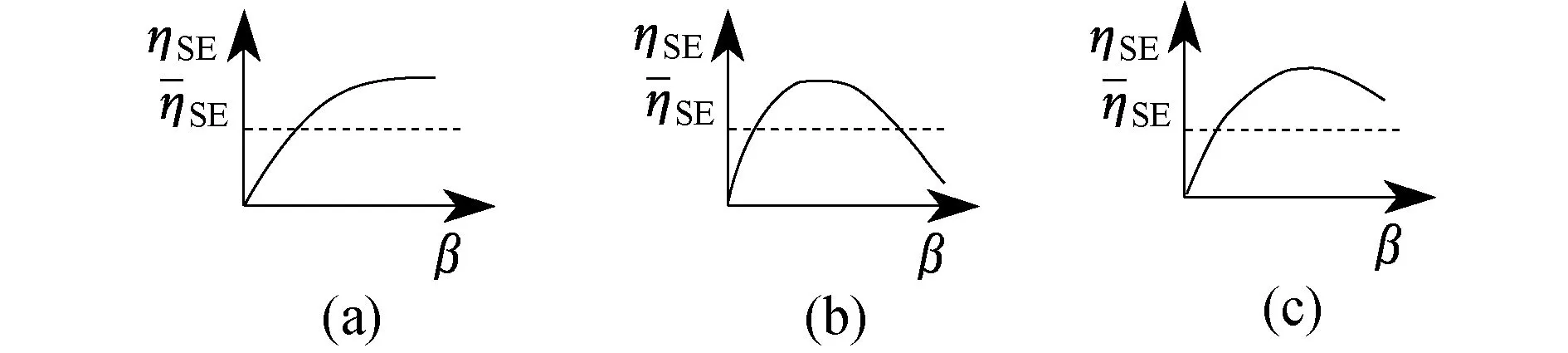
图2 函数ηSE与SE的3种关系

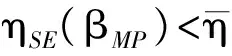
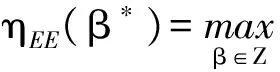
最后,将Dinkelbach算法和一维搜索结合,再进行循环迭代即可得到问题(10)的最优解.具体步骤如下:

步骤一:初始化设定最大循环次数Mmax,β初始值β1,最大允许误差δ1,循环次数变量j=1;

步骤四:j=j+1;

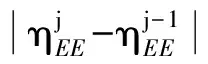
2.2 频效最大化的功率分配方案

求解使得SE最大时的各节点的功率,数学模型如下:

(14)

对于问题(14),同样可以采用迭代优化的算法来求得ηSE的最大值,即将(14)分解为求解以下两个问题

(15)

和

(16)

由2.1节知,(15)为凸优化问题,因此可以用Matlab Optimization Toolbox求得全局最优解,(16)的目标函数为关于β的凸函数,因此可以用一维搜索法求解,再采用2.1节的迭代算法,即首先将β作为定值,由(15)求得最优P1和P2,再将优化得到的P1和P2作为定值,由(16)求得最优β,如此反复迭代优化,直到最后的优化结果趋于收敛,优化完成.即可求得最大SE及对应的各节点功率.

3 仿真试验结果

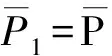
为了体现非最大功率发送对系统SE和EE的改善效果,图4～6比较了中继最大功率发送和中继非最大功率发送对SE和EE的影响.由图4可知,中继非最大功率发送对SE和EE均有改善,同时可以看出中继自干扰越多,最大EE和最大SE都越低.结合图5和图6可知,非最大功率发送对EE改善效果比SE更明显,这是因为非最大功率发送时会降低自干扰水平,无论对于SE和EE都能有一定改善,但是直观上由式(7～9)可以看出,发送功率对EE影响比对SE影响更明显,因此非最大功率发送对EE改善效果更明显.同时可以看出,无论中继设置在哪个位置上,非最大功率发送对EE和SE的改善效果都是一致的,即对EE的改善效果要好于SE.

图3 算法收敛性

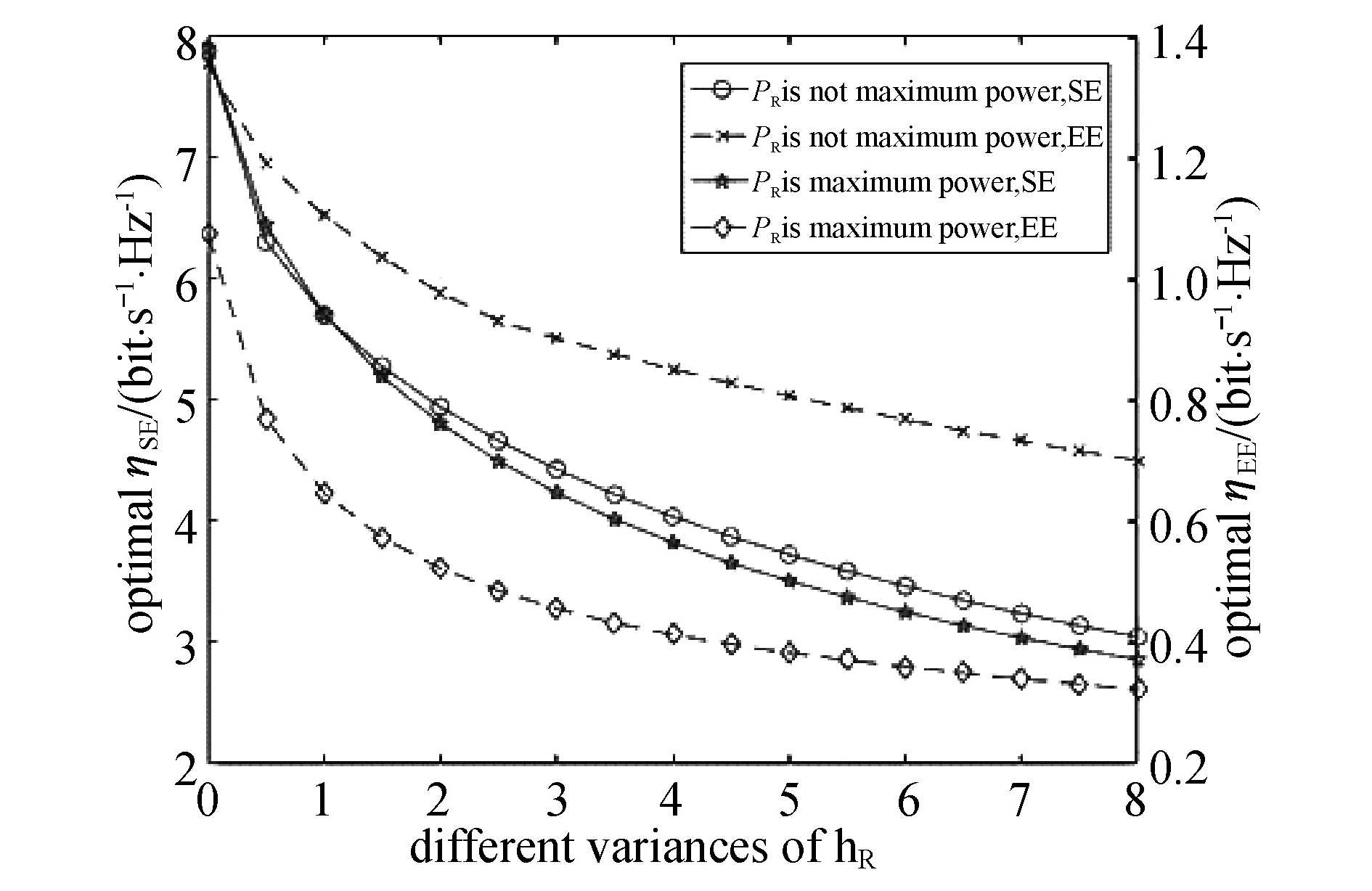
图4 不同自干扰水平下的最大EE和最大SE

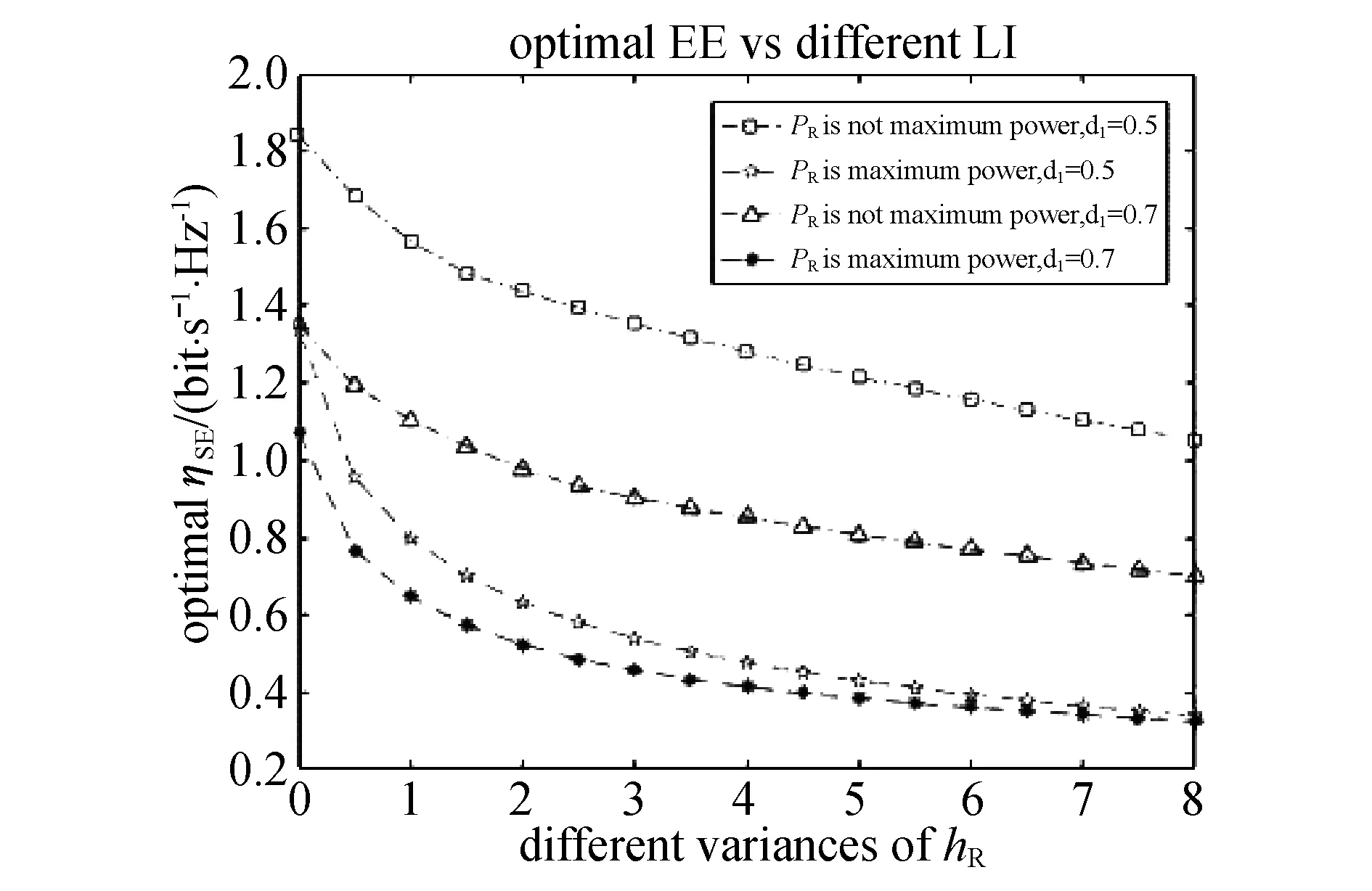
图5 不同距离及不同自干扰水平下的最大EE

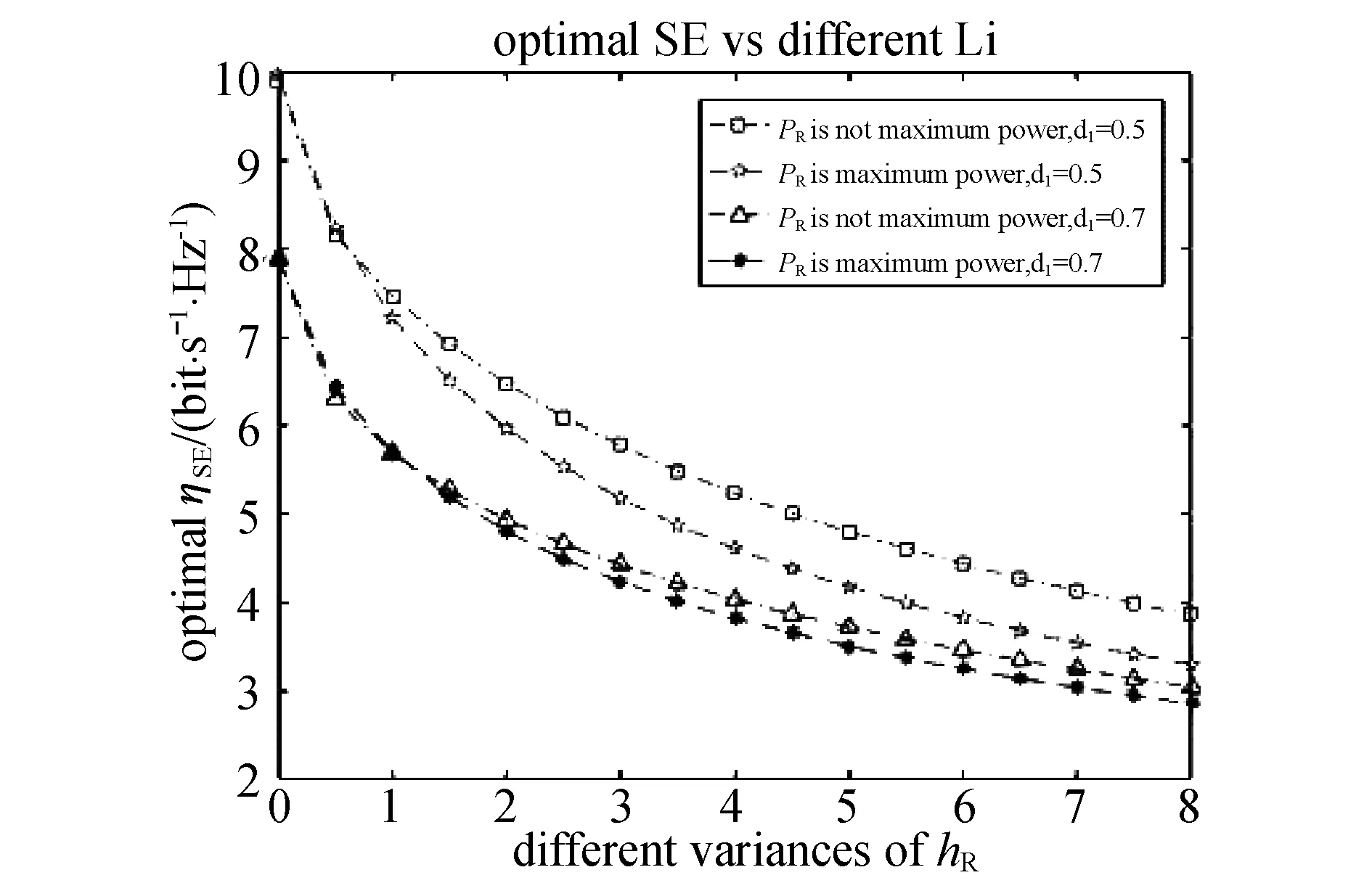
图6 不同距离及不同自干扰水平下的最大SE

4 结 论

本文作者研究了两种不同的功率分配方案分别对系统SE和EE进行优化,提出了基于Dinkelbach算法和一维搜索相结合的迭代算法.仿真结果表明,非最大功率发送对SE和EE均有改善效果,其中对EE改善效果更大.由此可以看出,在各节点非最大功率发送条件下,针对不同优化目标的功率分配方案都可以提高系统性能.

[1] Duarte M,Sabharwal A.Full-duplex wireless communications using off-the-shelf radios:Feasibility and first results [C].Conference Record of the Forty Fourth Asilomar Conference on Signals,Systems and Computers,Pacific Grove,2010.

[2] Riihonen T,Werner S,Wichman R.Comparison of Full-Duplex and Half-Duplex Modes with a Fixed Amplify-and-Forward Relay [C].IEEE Wireless Communications and Networking Conference,Budapest,2009.

[3] Li E,Zhang W,Sun J,et al.Energy-spectral efficiency tradeoff of visible light communication systems [C].IEEE.CIC International Conference on Communications in China,Chengdu,2016.

[4] Zhang Z,Chai X,Long K,et al.Full duplex techniques for 5G networks:self-interference cancellation,protocol design,and relay selection [J].IEEE Communications Magazine,2015,53(5):128-137.

[5] Chen H,Li G,Cai J.Spectral-energy efficiency tradeoff in full-duplex two-way relay networks [J].IEEE Systems Journal,2015,PP(99):1-10.

[6] Cheng X,Yu B,Cheng X,et al.Two-way full-duplex amplify-and-forward relaying [C].MILCOM.2013-2013 IEEE Military Communications Conference,San Diego,2013.

[7] Cui H,Ma M,Song L,et al.Relay Selection for two-way full duplex relay networks with amplify-and-forward protocol [J].IEEE Transactions on Wireless Communications,2014,13(7):3768-3777.

[8] Yahia E,Hamdi N.On maximization of energy efficiency in AF cooperative systems with imperfect CSI [C].IEEE.International Symposium on Communications and Information Technologies (ISCIT),Punjab,2016.

[9] Zhang Z,Chen Z,Shen M,et al.Spectral and energy efficiency of multipair two-way full-duplex relay systems with massive MIMO [J].IEEE Journal on Selected Areas in Communications,2016,34(4):848-863.

[10] Li Y,Li N,Peng M,et al.Relay power control for two-way full-duplex amplify-and-forward relay networks [J].IEEE Signal Processing Letters,2016,23(2):292-296.

[11] 邓乃扬.无约束最优化方法 [M].北京:科学出版社,1982.

[12] 陈宝林.最优化理论与算法 [M].北京:清华大学出版社,2005.

(责任编辑：包震宇,郁 慧)

Power allocation schemes for full-duplex two-way relay systems

Ge Jia, Qiu Mengting, Yu Hui

(School of Electronic Information and Electrical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Two power allocation schemes are presented to maximize SE and EE respectively.An iterative algorithm is used to solve the EE optimization problem.Firstly,the EEoptimization problem is transformed into a tractable non-fractional one by using the fractional programming method,and then the Dinkelbach algorithm is used to obtain the optimal power of the users,and then one-dimensional search is used to obtain the best relay amplification factor,and finally an iterative algorithm is used to maximize EE.SE optimization problem is also solved bythe iterative algorithm.The simulation results show that the two power allocation schemes aimed at different objective functions improve the EE and SE of the system respectively,and the iterative algorithm can converge quickly to obtain the optimal solution.

spectral efficiency; energy efficiency; full-duplex; two-way relay

10.3969/J.ISSN.1000-5137.2017.01.019

2016-12-12

国家科技支撑课题(2015BAD17B04)

葛 佳(1990-),女,硕士研究生,主要从事全双工双向中继和超密集小小区网络性能方面的研究.E-mail:gejia730@sjtu.edu.cn

导师简介: 俞 晖(1969-),男,高级工程师,主要从事无线通信技术方面的研究.E-mail:yuhui@sjtu.edu.cn(通信联系人)

TN 929.5

A

1000-5137(2017)01-0110-07