基于压缩感知的时频双选信道估计研究

涂玉良, 归 琳, 秦启波, 罗汉文

(上海交通大学 电子信息与电气工程学院,上海 200240)

基于压缩感知的时频双选信道估计研究

涂玉良, 归 琳, 秦启波, 罗汉文

(上海交通大学 电子信息与电气工程学院,上海 200240)

针对时频双选信道,利用信道的时间相关性,即同一条时延径在相邻时刻对应的信道系数之间具有很强的相关性,提出一种线性近似方法对时频双选信道进行建模,有效降低了未知参数的个数.考虑到无线信道在时延域具有稀疏性,基于压缩感知(Compressed sensing,CS)理论对线性近似模型进行了恢复重构.分别对未线性近似模型和线性近似模型的系统性能进行了仿真,并结合最小二乘(leastsquare,LS)算法、正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法、稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)算法给出了系统的归一化均方误差(Normalized Mean Square Error,NMSE)曲线.仿真结果显示,线性近似方法能有效对时频双选信道进行建模,针对本研究提出的线性近似模型,SBL算法能精确恢复出信道响应,并能有效地克服多谱勒效应.

时频双选信道; 信道估计; 压缩感知; 稀疏贝叶斯学习; 多谱勒效应

0 引 言

对于无线通信系统,信号在传播过程中会受到复杂地理环境的影响,接收端信号在幅度、相位和频率方面会发生不同程度的失真,无线信道往往呈现时频双重选择性衰落.正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术虽能有效克服频率选择性衰落,但其对多谱勒频偏非常敏感.针对时频双选信道,由于存在大量的未知信道参数,信道估计显得尤为困难[1].

传统的信道估计算法包括最小二乘法(Least Square,LS)算法,最小均方误差(Minimum mean square error,MMSE)算法,这些算法都是基于信道密集多径的特性.近年来,大量实验研究表明无线信道具有稀疏特性[2],因此可以利用信道的稀疏性减少传输导频的数量,提高信道估计的精度.对于稀疏信号的处理,压缩感知(Compressed sensing,CS)理论已经取得较大的发展,其利用低维的测量数据能对高维的稀疏信号进行精确恢复,常用的CS算法包括正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[3]、基追踪(Basis Pursuit,BP)算法[4]、稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)算法[5].然而,目前基于CS理论的信道估计研究主要集中在频率选择性信道,少有论文研究如何将CS理论用于时频双选信道估计.

本研究针对时频双选信道,基于信道系数在时间上的相关性,提出一种线性近似模型,并结合CS理论对未知信道系数进行恢复重构.仿真结果显示,本研究所提出的线性近似模型能有效对时频双选信道进行建模,基于CS理论的稀疏重构算法明显优于LS算法,其中,SBL算法对于所提模型具有很好的恢复性能.

1 压缩感知理论

CS技术是一种稀疏信号处理技术,其用远低于Nyquist采样定理要求的速率对信号进行采样、压缩和重构.

1.1 CS基本原理

(1)

对于式(1)表示的最优化问题,经典的解决算法是BP算法,其可采用传统线性编程技术实现.考虑到BP算法复杂度高,其他重构算法,例如OMP、SBL被广泛应用于稀疏信号重构问题.

1.2 系统模型

OFDM系统发送端结构如图1(a)所示.在发送端,首先,将串行比特流进行映射并转换成并行的比特流,并将导频符号插入到并行的比特流中;其次,通过OFDM调制将所得的并行比特流进行离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT),得到OFDM符号;然后,为了避免由于多径时延引起的符号间干扰,对每一个OFDM符号插入循环前缀(Cyclic Prefix,CP),其中CP的长度大于最大信道时延.最后将符号流进行并串转换后再进行发送.

令X=[X(0),…,X(N-1)]T为发送的OFDM符号,其中X(k)是第k个子载波上所发射的信息符号,N表示一个OFDM符号所具有子载波的数量.将X作IDFT变换后,时域的调制信号可以表示成x=FHX=[x(0),x(1),…,x(N-1)]T,其中F是离散傅里叶变换(DiscreteFourierTransform,DFT)矩阵,其第n行、第k列元素为wn,k=exp(-j2πnk/N),n,k=0,…,N-1.

图1 (a)发送机和(b)接收机的系统框图

OFDM系统接收端框图如图1(b)所示.在接收机,移除CP后,第n个采样时间接收信号可以表示如下:

(2)

其中L是信道的最大时延径,h(l,n)表示在第n个采样时间,收发机之间第l条路径下的脉冲响应,w(n)表示加性高斯白噪声.基于式(2),将N个连续的接收信号r=[r(1),…,r(N)]T表示如下:

(3)

其中w=[w(1),…,w(N)]T,HT是时域信道矩阵,其第p行第q列的元素表示如下:

(4)

将式(3)转换到频域,可得到频域接收信号:

(5)

时不变信道,HT是循环矩阵,H∈N×N的对角矩阵,W是加性高斯白噪声w的傅氏变换;对于时变信道,HT不再具有循环结构,H不是对角矩阵,从而接收信号之间存在载波间干扰(Inter-CarrierInterference,ICI),导致大量未知的信道系数需要估计,为了减少需要估计的系数个数,下文提出近似模型.

2 线性近似及稀疏重构

对于时频双选信道,在相邻时刻同一条时延信道系数之间具有很强的相关性,文献[9]提出了线性近似处理方法,用少量的系数对信道进行近似.当归一化多谱勒频移(NormalizedDopplerOffset)不超过0.2时,线性近似模型可以很好模拟信道的时变特性[10].

将式(5)通过使用克罗内克积(KroneckerProduct)的性质展开,得到:

(6)

Vec(ABC)=(CT⊗A)·Vec(B),

(7)

G⊗K代表两矩阵G和K的克罗内克积,IN表示N×N的单位矩阵[11],

(8)

是HT的第n列.考虑到信道在时延域的稀疏特性,设信道的非零时延径为K,满足K≪L[12],则Vec(HT)∈N2×1是一个稀疏向量,只有N×K个非零元素.

将(XT⊗IN)展开得到(XT⊗IN)=(XT⊗IN)D+(XT⊗IN)I,其中(XT⊗IN)D表示理想信号成分,定义如下:

(9)

(XT⊗IN)I表示载波干扰成分,定义如下:

(10)

从而可以将式(6)分解成如下模型:

(11)

将式(11)简化,表示如下:

(12)

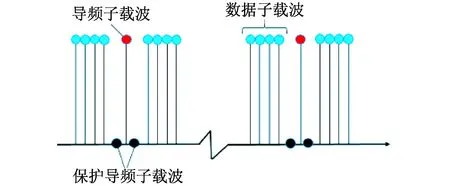
图2 系统导频模式

为了降低ICI的影响,设计系统导频模式如图2所示.在每个非零导频子载波左右各引入一个保护导频子载波.其中,非零导频子载波幅值设为1,保护导频子载波幅值设为0.基于设计的导频模式,可以近似忽略数据子载波对导频子载波的干扰,从而消除式(12)中的ICI项.

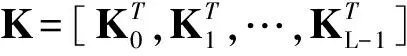
(13)

其中Mn,l∈N×N,其元素表示为:

(14)

注意到Kl表示第l条时延径相邻N个时刻对应的信道系数,其N个值存在高相关性,对Kl进行线性建模:Kl=C×Al对于第l条径,其中C、Al如下所示:

(15)

公式(15)中αl表示线性模型的斜率,表示如下:

(16)

基于上述线性近似模型,可以将K表示如下:

(17)

通过公式(12)和(17)得到最终的系统模型,表示如下:

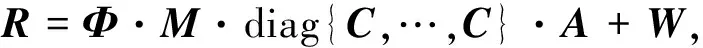
(18)

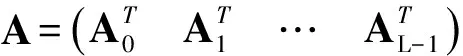
在下一节,基于本研究提出的线性近似模型(18),分别利用LS、OMP、SBL算法对信道系数进行恢复重建,通过实验仿真得到系统性能曲线.

3 实验结果与分析

3.1 实验基本说明与参数设置

针对时频双选信道,系统仿真参数设置如表1所示:

表1 仿真参数

其中,K个稀疏径随机分布在L个时延径中.仿真中用NMSE(λ)度量系统信道估计的性能,其定义如下:

(19)

实验分别对于不同的信噪比(Signal to Noise Ratio,SNR)和不同运动速度v,得到了系统的NMSE曲线.

3.2 实验结果与分析

实验中,针对本研究所提的线性近似模型(18),分别利用LS算法、OMP算法、SBL算法对信道系数进行恢复重构,作为对比,也对未经线性近似处理的时频双选信道模型(10)进行了相应的仿真,分别利用LS算法和OMP算法直接恢算得到信道系数Vec(HT).

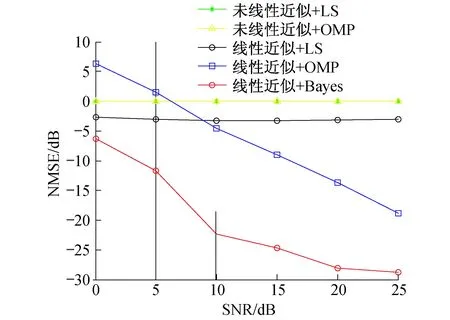
图3 在时速为120 km/h,系统均方误差与信噪比之间的性能曲线

对于SNR对NMSE性能的影响,设定移动速度v=120 km/h(fdoppler=333.4 Hz),实验仿真结果如图3所示.

从图3可以看出,对于未线性近似模型,通过LS、OMP算法得到的NMSE一直停留在0 dB,这是由于未线性近似模型(12)中,未知非零系数个数为K×N,远大于观测向量的个数G,因此系统无法恢复得到信道系数.对于线性近似模型,LS算法性能很差,这是由于LS算法没有利用到信道的稀疏特性,OMP算法在低信噪比时性能差是因为其受噪声影响较大;SBL算法能得到很好的性能,例如当SNR为15 dB时,相比于LS算法,SBL算法能使NMSE降低22 dB,相比于OMP算法,SBL算法能使NMSE降低15 dB.

对于速度v对NMSE性能的影响,设定SNR为15 dB,实验仿真结果如图4所示.

图4 信噪比是15 dB,系统均方误差与速度之间的性能曲线

由图4可知,随着移动速度增加,系统的NMSE性能变差,这是由于速度增加使得多普勒频移增大,从而系统ICI变得更严重,导致信道估计精度降低.和图3类似,同样可以发现对于未线性近似的模型,系统性能很差;对于线性近似模型,LS算法性能较差,其NMSE保持在-3 dB上;OMP算法的NMSE曲线随着速度的增大而缓慢增加,其较LS算法而言,能有效克服多谱勒频偏对系统性能的影响;SBL算法性能最好,表现出良好的抑制多谱勒效应的性能.

4 结束语

对于时频双选信道,由于其存在大量的未知参数,利用传统的信道估计方法会产生巨大的导频开销,极大降低系统资源利用率.本研究基于信道的时间相关性,提出了一种线性近似模型,并利用信道在时延域的稀疏特性,基于CS理论对时频双选信道进行信道估计,降低了系统的导频开销,从而使得系统的资源利用率得到提高.实验中,分别对未线性近似模型和线性近似模型的系统性能进行了仿真,利用LS算法、OMP算法、SBL算法等对模型进行稀疏系数重构.仿真结果显示,所提线性近似模型能很好地对时频双选信道进行建模,且基于CS理论的SBL算法能有效的恢复出信道响应,在SNR大于15 dB条件下其NMSE能达到-25 dB以下,性能明显要优于其他算法;对于所提线性近似模型,SBL算法对不同的移动速度v都表现出很好的恢复性能,能有效克服多谱勒效应.

[1] Cheng P.Channel estimation for OFDM systems over doubly selective channels:A distributed compressive sensing based approach [J].IEEE Transactions Communication,2013,61(10):4173-4185.

[2] Gao Z,Zhang C,Wang Z,et al.Priori-information aidediterative hard threshold:A low-complexity high-accuracy compressivesensing based channel estimation for TDS-OFDM [J].IEEE Transactions Wireless Communication,2015,14(1):242-251.

[3] Trop J A,Gillbert A C.Signal recovery from random measurements via orthogonal matching Pursuit [J].Information Theory IEEE Transactions,2007,53(12):4655-4666.

[4] Chen S S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit [J].SIAM Journal on Scientific Computing,1998,20(1):33-61.

[5] Suryaprakash R T,Pajovic M,Kin K J,et al.Millimeter wave communication channel estimation via Bayesian group sparse recovery [C].IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP),2016,10:3403-3410.

[6] Donoho D,Elad M,Temlyakov V.Stable recovery of sparse overcomplete representations in the presence of noise [J].IEEE Transactions on Information Theory,2006,52(1):6-18.

[7] Candes E J,Romberg J,Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information [J].IEEE Transactions on Information Theory,2006,52(2):489-509.

[8] Fornasier M.Numerical methods for sparse recovery [J].Theoretical Foundations and Numerical Methods for Sparse Recovery,2010,14:93-200.

[9] Qin Q B,Gui L,Gong B,et al.Structured distributed compressive channel estimation over doubly selective channels [J].IEEE Transactions on Broadcasting,2016,62(3):521-531.

[10] Mostofi Y,Cox D C.ICI mitigation for pilot-aided OFDM mobile systems [J].IEEE Transactions Wireless Communication,2005,4(2):765-774.

[11] Brewer J W.Kronecker products and matrix calculus in system theory [J].IEEE Transactions on Circuits and Systems,1978,25(9):772-781.

[12] Bajwa W U,Haupt J,Sayeed A M,et al.Compressed channel sensing:a new approach to estimating sparse multipath channels [J].Proceedings of the IEEE,2010,98(6):1058-1076.

(责任编辑：包震宇,郁 慧)

Time-frequency doubly selective channel estimationbased on compressed sensing

Tu Yuliang, Gui Lin, Qin Qibo, Luo Hanwen

(School of Electronic Information and Electrical Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

In this paper,considering time-frequency doubly selective channel,we utilize the channel’s time correlation that the channel coefficientscorresponding tothe neighboring instants have a strong correlation.And we present a linear approximation method,which effectively reduces the number of unknown parameters.Considering the sparseness of the wireless channel in the delay domain,this paper reconstructs unknown channel parameters of the proposed model based on compressed sensing (CS) theory.In the simulations,we observe the system performance of the linear approximation model and the non-linear approximation model,respectively,and present the normalized mean squared error (NMSE) curves based on the least square (LS),orthogonal matching pursuit (OMP) and sparse Bayesian learning (SBL) algorithms.Simulation results show that the linear approximation method can effectively model the time-frequency doubly-selective channels.For the proposed linear approximation model,SBL algorithm can accurately recover the channel response,and overcome the Doppler effecteffectively.

time-frequency double selection channel; channel estimation; compressed sensing; bayesian learning; doppler effect

10.3969/J.ISSN.1000-5137.2017.01.017

2016-12-15

国家自然科学基金(1471236,61420106008,61671295);111计划(B07022);上海浦江人才计划(16PJD029)

涂玉良(1992-),男,硕士研究生,主要从事MIMO无线通信空间调制技术方面的研究.E-mail:tyliang@sjtu.edu.cn

导师简介: 归 琳(1975-),女,教授,主要从事高速移动通信,宽带机动通信网,栅格通信网,下一代数字电视广播技术方面的研究.E-mail:guilin@sjtu.edu.cn(通信联系人)

TN 929.5

A

1000-5137(2017)01-0098-06