基于取样光纤光栅的温度-应变交叉传感器

张笑航, 武向农

(上海师范大学 信息与机电工程学院,上海 200234)

基于取样光纤光栅的温度-应变交叉传感器

张笑航, 武向农

(上海师范大学 信息与机电工程学院,上海 200234)

设计了一种基于取样光纤光栅的温度-应变交叉传感器,应变测量范围为0～2 000 με,温度测量范围为-50～200 ℃.仿真验证获取了取样光纤光栅的传感特性.应用SPSS统计学软件,得到取样光栅同时测量温度和应变的双参量矩阵方程,并标定了矩阵方程中的4个传感系数.

光纤传感; 取样光纤光栅; 交叉敏感; 传输矩阵法

0 引 言

光纤光栅传感器一直存在应变-温度交叉敏感问题.由于布拉格波长对应变和温度都是敏感的,从单个布拉格波长的变化量中难以分辨出应变和温度各自的变化量[1].目前,交叉敏感问题的解决方法主要为单一参量补偿和双参量区分补偿[2].文献[3]设计了一种双参数FBG传感器,可以同时测量温度和应变,温度灵敏度为12.2 pm/℃,封装后的应变灵敏度为1.79 pm/με,但其几乎不可能制造出完全相同的2个FBG传感器.文献[4]提出了基于双三角形悬臂梁结构的FBG 双参量传感器,通过测定光纤光栅反射谱的双峰位置,实现了单光栅应变和温度的同时检测,应变、温度传感灵敏度分别为0.125 nm/με,0.0124 nm/℃,但该方法需要2套独立的解调系统,增加了系统的复杂性.

取样光纤光栅是一种理想的多参量传感元件,因其反射谱有一组分立的反射峰,在温度和应变变化时,反射峰的波长会发生不同的变化,因此可以利用取样光纤光栅实现温度和应变的双参量测量,克服交叉敏感问题[1].针对文献[3]、[4]中出现的问题,本文作者采用传输矩阵法,构造可用于传感的取样光纤光栅,通过OptiGrating软件进行了取样光纤光栅传感特性的仿真实验,分别获取了取样光纤光栅温度和应变传感仿真数据,并在此基础上,将应变和温度这两个参量相结合,采用回归分析法,应用SPSS软件研究分析了取样光纤光栅温度、应变传感特性,得到了取样光纤光栅测量温度和应变的双参量矩阵方程,并标定了测量矩阵方程的4个传感系数.通过测量反射光谱的反射率变化值和波长漂移量,只需一套解调系统,就能够实现单根取样光纤光栅同时测量应变和温度,从而解决了温度-应变交叉敏感问题.

1 理论分析

对于非均匀光纤光栅,传输矩阵法的求解过程直观简单:将一个非均匀周期的光纤光栅看成是由一系列均匀周期的小段光纤光栅级联而成的,将它们的传输矩阵相乘,即得到光纤光栅的总传输矩阵及传输特性的数学表达式[5].

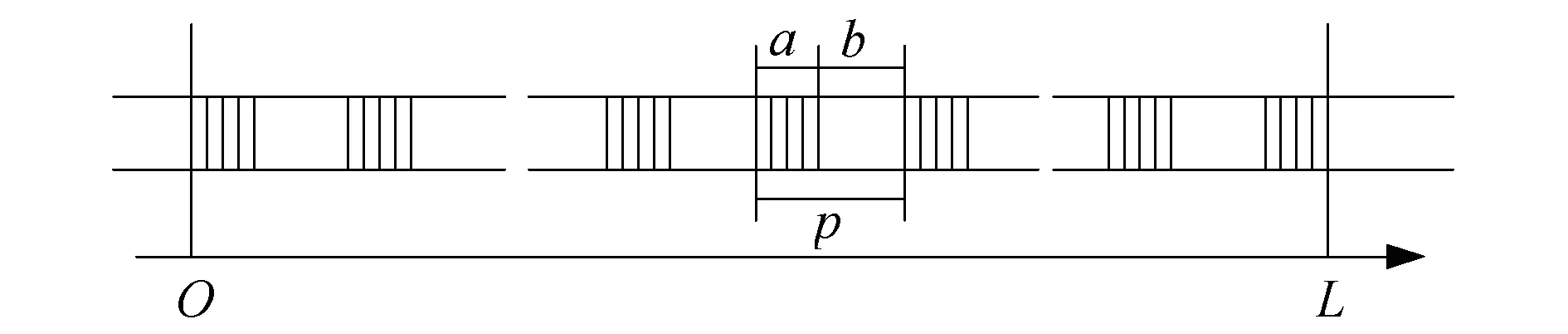
图1 取样光纤光栅结构示意图

一段长度为L的矩形取样光纤光栅的结构模型如图1所示,其中光栅取样周期为p=a+b,a为曝光区长度,b为非曝光区长度,占空比为T=a/b,周期个数为n=L/p.

当光束经过第j小段均匀光纤光栅后可用传输矩阵法表示为[5]:

(1)

(2)

光束经过第j小段非曝光区后只是产生了相应的相位延迟,可用传输矩阵法表示为[5]:

(3)

(4)

其中,β=2πneff/λ为传播常数.

同理,经过n个取样周期后,光束通过一段长度为L的取样光纤光栅的传输矩阵关系表示为[5]:

(5)

利用边界条件Rn=R(0)=1和S0=S(L)=0,可得到取样光纤光栅的反射率:

(6)

2 传感特性仿真实验与数据分析

使用加拿大公司Optiwave制作的模拟软件OptiGrating来做取样光纤光栅的传感特性仿真实验,通过改变取样光栅总长度、占空比、折射率调制强度和取样周期等参数,可以构造出可用于传感的取样光纤光栅.

为了使仿真实验更加贴近实际情况,参考了北京虹林光电科技有限公司所设计的取样光纤光栅,其中心波长为1 510～1 590 nm,反射率大于90%,3 dB带宽小于0.23 nm,栅区长度为10 mm,光纤类型可选,光栅数量为1～20.基于这些真实器件的参数,实验中,将取样光纤光栅的各参量分别设置为:取样光栅总长度L为10 mm,占空比T为0.3,取样周期为200 μm,其中曝光区长度为60 μm,非曝光区长度为140 μm,折射率调制深度δneff为0.0005,热光系数为8.3×10-6/℃,热膨胀系数为5.5×10-7/℃.同时,本次仿真选取了Corning公司的SMF-28型光纤作为实验光纤,其纤芯半径为4.15 μm,包层半径为62.5 μm.对于中心波长为1 550 nm的光来说,SMF-28型光纤纤芯折射率为1.46,包层折射率为1.45.

2.1 应变传感特性仿真实验

在取样光纤光栅应变传感实验中,仿真环境温度设置为25 ℃,应变初始值则为0 με,之后仿真过程中应变每增加100 με,对取样光纤光栅反射谱进行一次仿真测量.实验得到的部分取样光纤光栅反射谱如图2所示.

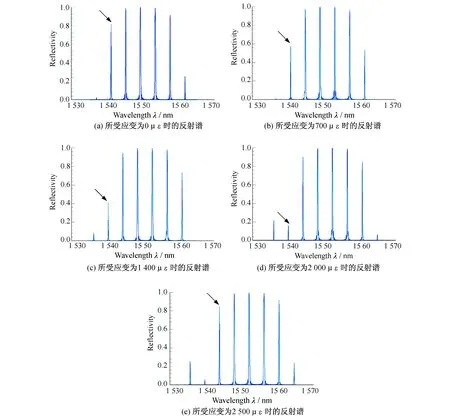
图2 仿真实验中取样光纤光栅在不同应变下的反射谱

从图2可以看出,取样光纤光栅反射谱中共有6个主反射峰,并且,相邻2个反射峰的间隔并不受外界应变改变的影响,Δλ保持恒定,约为4.08 nm.通过对图2中取样光纤光栅反射谱的比较,6个主反射峰中,中间4个反射峰的峰值变化并不明显,相比而言,第一和第六个反射峰的变化较为明显,通过对这两个反射峰的研究发现,第一和第六个反射峰为周期性变化的两个阶段,总体趋势为反射峰的峰值先减小,后增大.因此,为了方便计算,选取第一个反射峰(图2中箭头所指)作为参考反射峰.经过观察发现随着所受应变的增加,第一个主反射峰的位置逐渐向左边移动,即向着波长减少的方向移动.同时,第一个主反射峰的峰值也呈减小的趋势,但是其减小是有范围的,从图2(e)中可以看出,当取样光纤光栅所受应变为2 500 με时,第一个主反射峰的峰值已恢复到图2(a)中的强度.因此,使用取样光纤光栅进行应变测量时,应该事先测量所选用反射峰的测量范围,选用0～2 000 με作为良好线性范围.

第一个主反射峰应变传感特性仿真实验数据如表1所示.

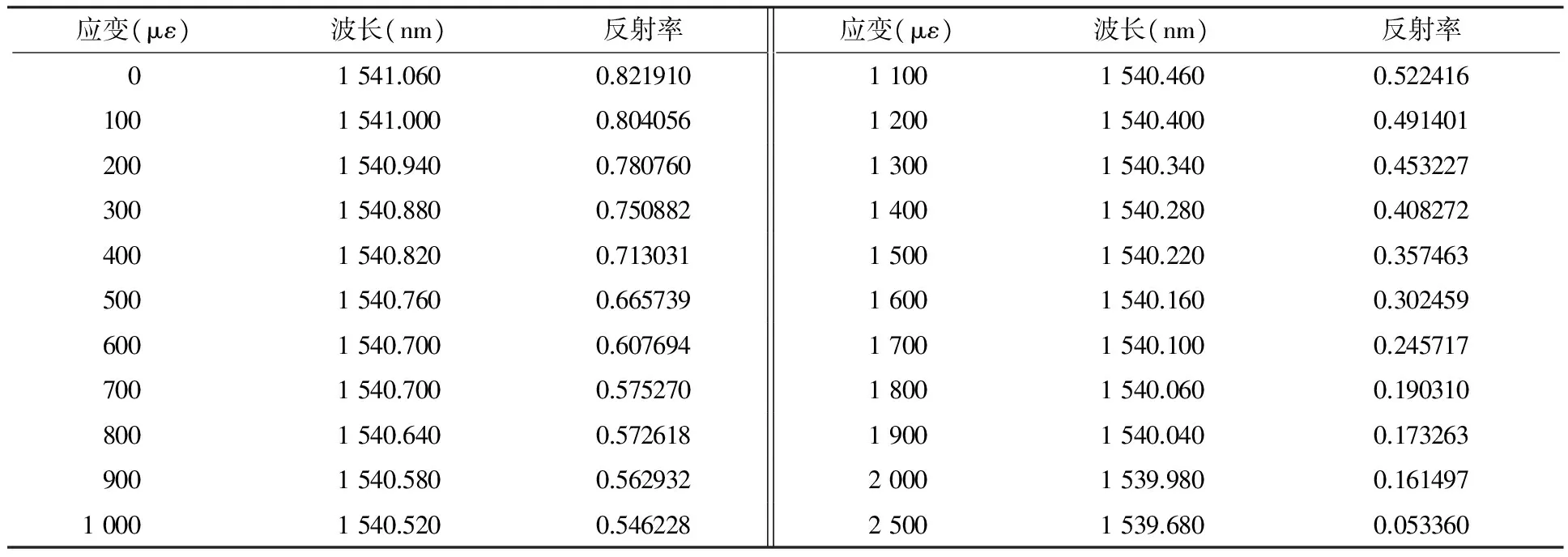
表1 应变传感特性仿真实验数据

2.2 温度传感特性仿真实验

在取样光纤光栅温度传感实验中,仿真环境应变设置为0 με,考虑到所设计的取样光纤光栅温度-应变传感器会被应用在寒冷或炎热地域,因此温度初始值设置为-50 ℃,而温度的上限则限制在200 ℃,仿真过程中温度每增加10 ℃,对取样光纤光栅反射谱进行一次仿真测量.实验得到的部分取样光纤光栅的反射谱如图3所示.

图3 仿真实验中取样光纤光栅在不同温度下的反射谱

从图3可以看出,取样光纤光栅反射谱中共有6个主反射峰,并且,相邻2个反射峰的间隔并不受外界温度改变的影响,Δλ保持恒定,约为4.08 nm.通过对图3中取样光纤光栅反射谱的比较,6个主反射峰中,中间4个反射峰的峰值变化并不明显,相比而言,第一和第六个反射峰的变化较为明显,通过对这两个反射峰的研究发现,第一和第六个反射峰为周期性变化的两个阶段,总体趋势为反射峰的峰值先减小,后增大.因此,为了方便计算,选取第一个反射峰(图3中箭头所指)作为参考反射峰.经过观察发现随着所受温度的增加,第一个主反射峰的位置逐渐向右边移动,即向着波长增加的方向移动.同时,第一个主反射峰的峰值也呈减小的趋势,但是趋势并不明显,这是由于构造取样光纤光栅的小段光栅的应变灵敏度要高于温度灵敏度.

第一个主反射峰温度传感特性仿真实验数据如表2所示.

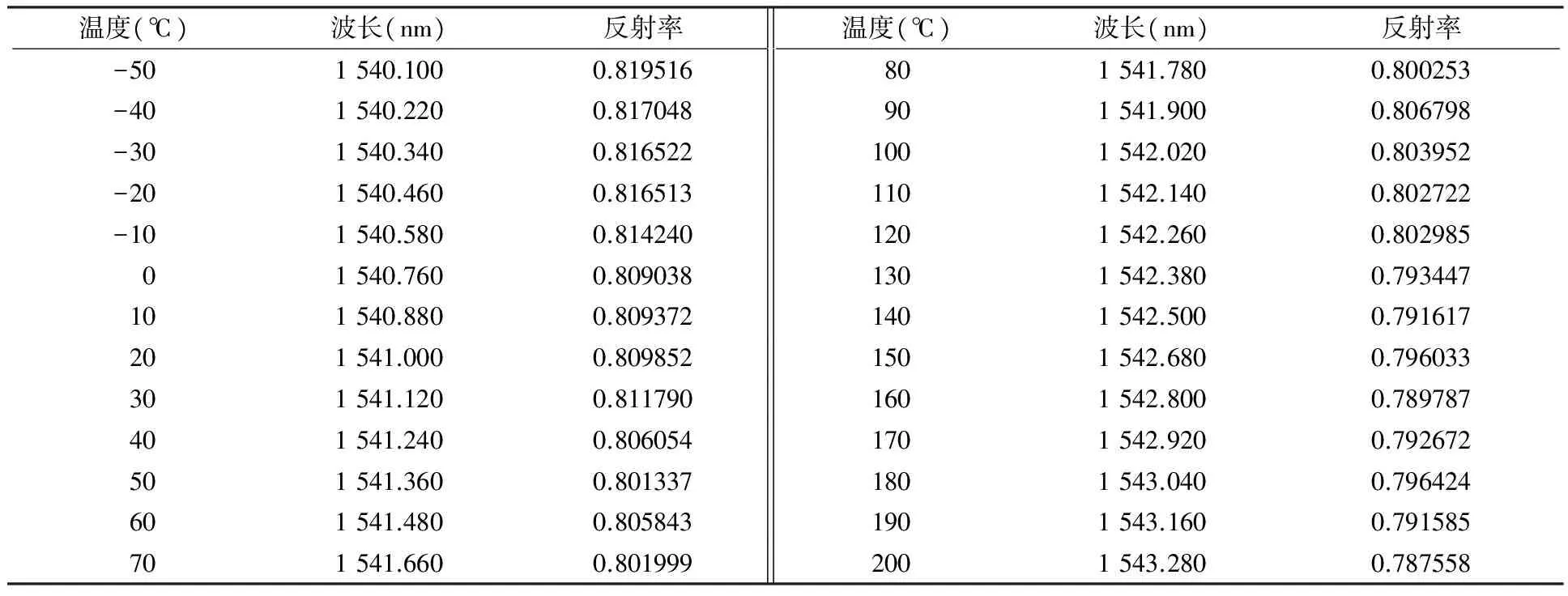
表2 温度传感特性仿真实验数据

2.3 传感特性分析

通过上述两个仿真实验,观察到应变和温度可以同时引起取样光纤光栅反射谱中反射峰波长的漂移和反射峰峰值(反射率)的变化,所以基于反射谱的这个特性,可以构造出可用于传感的取样光纤光栅传感器及相应的传感解调系统,实现对温度和应变的同时测量.同时,从上述仿真实验结果可以得出,在一定的应变或温度范围内,反射率的变化值和反射峰波长的漂移量与温度和应变变化量可以拟合成线性关系,这样就可以建立起一个温度-应变双参量测量矩阵方程如式(7)所示.

(7)

其中A、B、C和D是由传感特性仿真实验确定的传感系数,Δε为所受应变的变化值,ΔT为温度的变化值,ΔR为反射率,Δλ为反射峰的波长漂移量.若令ΔT=0,则式(7)中第一个待定系数方程变为ΔR=AΔε,则A=ΔR/Δε,ΔR/Δε是取样光纤光栅反射率对应变的灵敏度,因此只需求出ΔR/Δε,就可以得到A的值,其余B、C和D的值同理可得.最后,通过求解该测量矩阵方程,就可以分别解出ΔT和Δε的值,由此求出了环境温度和应变的变化值.

2.4 仿真实验数据处理

SPSS软件是一款统计软件,用它处理回归试验设计中的数据比较简单方便,结果清晰明确.通过SPSS 软件,可以省去繁杂的计算过程[6].使用SPSS 22.0的回归分析模块对双参量矩阵方程组进行求解,可得出传感系数A、B、C和D.线性回归结果如表3～6所示.

表3 传感系数A回归结果

注:因变量为反射率

表4 传感系数B回归结果

注:因变量为反射率

表5 传感系数C回归结果

注:因变量为波长

表6 传感系数D回归结果

注:因变量为波长

表4～6中,B为回归系数,Beta为标准回归系数,二者作用均为预测自变量和因变量之间的相关性;T是对回归系数B进行T检验的结果,Sig则是T检验的显著性,一般来说,T的绝对值越大,则Sig就越小.统计上,Sig<0.05就被认为是系数检验显著,显著的意思为回归系数绝对值显著大于0.

最终,利用SPSS的拟合模块对实验结果进行线性拟合,可以得到反射率对应变、温度以及波长对应变、温度的线性拟合图,如图4所示.

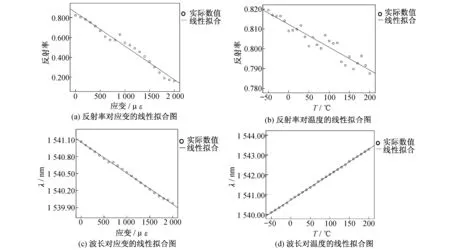
图4 SPSS中的各变量线性拟合图

图4(a)～(d)的斜率分别为ΔR/Δε,ΔR/ΔT,Δλ/Δε,Δλ/ΔT,由2.3分析可知,分别对应式(7)中A、B、C和D的值为-0.000337/με,-0.000115/℃,-0.000545 nm/με和0.012806 nm/℃.同时,由2.1和2.2可知,应变测量范围为0με～2 000με,温度测量范围为-50 ℃～200 ℃.

因此最后得到取样光纤光栅温度-应变双参量测量矩阵方程:

(8)

实际使用中,把测量出的取样光纤光栅反射谱中的反射率变化值和波长漂移量代入式(8),就可以求出环境温度和应变的变化值.由此,实现了取样光纤光栅对温度和应变这两个参量的同时测量.

2.5 误差分析

实际测量中,如果不考虑温度的影响,只分析取样光纤光栅轴向应变的情况,那么测量误差主要来自于:光源功率波动误差、耦合器误差以及探头误差[1].首先,放大自发辐射(ASE)光源具有全局光反馈功率控制及脉宽调制精密温控技术,可以减小由于光后向散射和偏振耦合引起的相干噪声,但还是存在不稳定性,具体为其输出的光功率和波长有一定的波动,将会引起取样光纤光栅反射谱的偏移和波动.其次,耦合器的性能参数主要有插入损耗,附加损耗,分光比,偏振相关损耗及方向性,这些参数都会对解调精度造成一定的影响.最后,实验中,需要测量取样光纤光栅反射谱中的反射率变化值和波长漂移量,然后通过求解双参量矩阵方程得到环境温度和应变的变化值,若灵敏度不够高,则会造成波长和反射率的测量误差.

其实,能够影响环境温度和应变测量的因素有很多,如:交叉干扰、非线性效应、取样光纤光栅的写入技术、交叉干扰及传感解调系统中各元器件连接损耗等[1],这些问题都是造成取样光纤光栅传感器尚无法大规模应用的原因.

3 结 论

本文作者利用传输矩阵法,选择合适的参数,设计出一种可用于传感的取样光纤光栅,利用OptiGrating软件,通过仿真实验,分别获取了取样光纤光栅反射光谱在不同温度和应变下的波长及反射率变化的仿真数据,并在此基础上,将温度和应变这两个参量相结合,采用回归分析法,利用SPSS软件研究分析了取样光纤光栅温度、应变的传感特性,得到了取样光纤光栅测量温度和应变的双参量矩阵方程,并标定了矩阵方程中的4个传感系数A,B、C和D,分别为-0.000337/με,-0.000115/℃,-0.000545 nm/με和0.012806 nm/℃.主要创新工作在于:构造了适合传感的取样光纤光栅,在测量环境温度和应变时,只需要通过测量取样光纤光栅反射谱的反射率变化值和波长漂移量,就能得到温度和应变的变化值.文献[7]所设计的超结构FBG传感器需将要FBG和LPG级联后进行对比分析,而本研究只需一套解调系统,仅用单根取样光纤光栅就实现了环境应变和温度的同时测量.并且,本研究所设计的取样光纤光栅虽然应变灵敏度下降了0.25 pm/με,但温度灵敏度提高了4.14 pm/℃.考虑到所设计的取样光纤光栅传感器需要应用于气候条件严苛的地区,因此将应变的测量范围定为0～2 000 με,而温度测量范围则扩大至-50～200 ℃,使得所设计的取样光纤光栅传感器适应性更强,可应用于各种复杂气候环境.

[1] Zhu D D.Study of sampled grating reflective spectrum based photonic crystal theory and fiber grating sensing technology [D].Qinhuangdao:Yanshan University,2010.

[2] Zhang D P,Zheng Y,Wang J,etal.Investigation of cross-sensitivity of fiber Bragg grating temperature sensor [J].Journal of Atmospheric and Environmental Optics,2016,11(3):226-233.

[3] Wang Z B,Yang P L,Shao B B,et al.Fiber Bragg grating for simultaneous measurement of strain and temperature [J].Laser & Optoelectronics Progress,2013.50(10):1-5.

[4] Zhang J L,Yu C X,Wang K Z,Li C,A fiber grating dual-parameter sensor of ditrigon cantilever beam for measurement of strain and temperature [J].ActaPhotonicaSinica,2009.38(4):770-774.

[5] Wang L,Wu X,The research on Sagnacloop microwave photonic filter based on fiber Bragg grating [D].Shanghai:Shanghai Normal University,2015.

[6] Zhu D D,Wang H F,Li Z Q,et al.Study on sampled fiber grating sensing characteristic based on regression analysis [J].Chinese Journal of Sensors and Actuators,2007,20(12):2579-2582.

[7] Sengupta S,Ghorai S K.Design of superstructure fiber Bragg grating with efficient mode coupling for simultaneous strain and temperature measurement with low cross-sensitivity [J].IEEE SensorsJournal,2016,16(15),7941-7949.

[8] Elgaud M M,Zan M S D,Abushagur A A G,et al.Analysis of independent strain-temperature fiber Bragg grating sensing technique using optisystem and optigrating [C]//IEEE.2016 International Conference on Photonics,Sarawak:IEEE,2016.

[9] Lv L,Wang S,Jiang L,et al.Simultaneous measurement of strain and temperature by two peanut tapers with embedded fiber Bragg grating [J].Applied Optics,2015,54(36):10673-10678.

[10] Liu Q,Ran Z L,Rao Y J,et al.Highlyintegrated FP/FBG sensor for simultaneous measurement of high temperature and strain [J].IEEE Photonics Technology Letters,2014,26(17):1715-1717.

[12] Song D,Chai Q,Liu Y,et al.A simultaneous strain and temperature sensing module based on FBG-in-SMS [J].Measurement Science and Technology,2014,25(5):55205-55210.

[13] Alemohammad H R,Foroozmehr E,Cotten B S,et al.A dual-parameter optical fiber sensor for concurrent strain and temperature,measurement:design,fabrication,packaging,and calibration [J].Journal of Lightwave Technology,2013,31(8):1198-1204.

[14] Li H.High channel-count comb filter based on sampled fiber Bragg grating [C].Information ScienceSignal Processing and Their Application (ISSPA),2012(11):1401-1404.

[15] Zhao M F,Wang S F,Luo B B,et al.Theoretical study on the cross sensitivity of fiber Bragg grating sensor affected by temperature and transverse pressure [C]//IEEE.Photonics and Optoelectronic,Chengdu:IEEE,2010.

(责任编辑：包震宇)

Design of cross-sensitive temperature and strainsensor based on sampled fiber grating

Zhang Xiaohang, Wu Xiangnong

(College of Information,Mechanical and Electrical Engineering,Shanghai Normal University,Shanghai 200234,China)

In this paper,a cross-sensitive temperature and strain sensor based on sampled fiber grating is designed.Its temperature measurement range is -50-200 ℃,and the strain measurement rangeis 0-2 000 με.The characteristics of the sensor are obtained using simulation method.Utilizing SPSS software,we found the dual-parameter matrix equations of measurement of temperature and strain,and calibrated the four sensing coefficients of the matrix equations.

optical fiber sensing; sampled fiber grating; cross-sensitivity; transfer matrix method

10.3969/J.ISSN.1000-5137.2017.01.012

2016-11-29

上海市教育委员会科研创新项目(14YZ070)

张笑航(1992-),男,硕士研究生,主要从事光纤传感方面的研究.E-mail:864792774@qq.com

导师简介: 武向农(1970-),女,副教授,主要从事光纤通信和光纤传感等方面的研究.E-mail:xnwu@shnu.edu.cn(通信联系人)

TP 212.1

A

1000-5137(2017)01-0066-08