基于弹性接触的共轭梯度算法

余小刚, 杜俊怀

(南京理工大学 理学院，南京 210094)

基于弹性接触的共轭梯度算法

余小刚, 杜俊怀

(南京理工大学 理学院，南京 210094)

为了解决有约束的基于共轭梯度二次规划算法的多次迭代问题，结合共轭梯度算法和有效集策略，提出了一个新的算法模型，通过对变量的截取(使用Polak-Bibiere 公式)来避免重新开始共轭梯度算法，在大规模的弹性接触问题中，大量的结果表明了这个算法的有效性。

凸规划;条件约束;共轭梯度算法;有效集策略;弹性接触问题

两个弹性体接触时会发生形变，这时就产生了形变势能和外力势能，由平衡状态时的总势能处于极小值的条件导出变分方程，就得到有约束的一个二次凸规划问题。在满足连续性以及接触面不可穿透条件的所有位移场中，接触物体的物理状态满足最小化属性。

针对二次规划和更一般的凸规划，有许多的解决策略，主要有内点法和有效集策略(Hager W (2006), Bertsekas D(1999))[1-2]。由于后面一种算法在处理问题的时候更简单，所以更受青睐。有效集策略在解决凸规划问题中，利用了一系列的子问题，其中不等式约束(非有效约束)被忽略，简单地用等式(有效约束)来替代。针对凸规划这些子问题有更简单的结构，因为约束条件都是等式约束，最优解只需要满足这些等式约束即可。针对凸规划，有效集策略还有一个更好的特性，即算法中采用的变量可以很好地解释其物理意义。

在解决大型的线性系统AX=b的问题中(A是正定矩阵)[3-4]，共轭梯度算法是一个非常重要的方法。它使用起来比较简单，收敛性也很好，收敛速度是典型的超线性收敛。平常应用时通常会引进一些预设条件来进一步提高它的收敛速度，因此有效集策略里出现的线性系统问题通常都是用共轭梯度算法来求解。更简单的考虑是利用不精确的解，在精确解求出来之前停止迭代，共轭梯度算法和有效集策略相互交织一起使用。

目前，基于共轭梯度法的一些算法需要很多次迭代，这些算法在扩大有效集的时候显得格外谨慎，而且被多次重启共轭梯度算法所阻碍，这是有效集策略带来的缺点。如果过大地改变有效集，就可能导致在迭代过程中出现死循环。这意味着有效集算法在迭代过程中，可能过一个周期后，就会找到之前迭代的点，这样一直循环，从而找不到最优解。

1 问题构造

1.1 连续问题构造

所考虑的两个接触物体具有各向同性、均匀和完全弹性的要求，接触面相对于物体本身的尺寸是很小的(集中接触)。外表面法线被定义为nα，其中α=1,2是物体的编号。外表面法线几乎穿过所有接触面，参考点就选在接触面上或接触面附近。定义一个笛卡尔坐标系oxyz，其中z轴和n2的方向一致，都指向物体Ⅰ。

两个物体接触面上一个接触点对X的位移记作uα(X)，应力记为pα(X)。两个接触的物体，对接触面上的任一点有p(2)(X)=-p(1)(X)总是成立的，所以可以不考虑p(2)(x)，只考虑单变量p(X)=p(1)(X)。进一步，由于位移在法线方向上不同，所以引进一个相对位移，u(X)=u(1)(X)-u(2)(X)。

本篇文章中，考虑的是无摩擦的正常弹性接触问题，主要考虑p和u在法线方向上的分量。

在未发生变形时定义几何平面作为参考平面，两个物体表面上的点相对于参考平面的距离为h1(x,y)和h2(x,y)，于是给出未变形的距离h=h(1)-h(2)，所以两个面的间隙(距离)在接触后为

e=h+u

(1)

主要关注的情况为h是完全确定的，不同的情况对应不同h值。对于平面oxy定义一个子集H作为可能潜在的接触面，这个区域分为实际已经接触的部分和外部没有接触的部分ε，由此可以得到一个接触的条件，定义如下：

∀X∈ε:e≥0,p=0

(2)

∀X∈:e=0,p>0

(3)

式(2)和式(3)表明法线方向的应力是相互的，而且两个物体是没有相互渗透的。当然，也存在两个物体的黏附力太大，导致p<0，在实际情况中，黏附力都是很小的，可以直接忽略。一种例外情况是，两个物体都非常光滑，而且其中一个由非常软的材质构成，或者在微观尺度研究这些关系。在半空间中，p和u通过Boussinesq积分给出：

(4)

A(X,Y)是法向位移和法向应力分量的影响方程，G和v分别是材料的弹性模量和泊松比。注意到A(x,y) 仅仅与x和y的相对位置有关,是等式(4)卷积公式的第一部分，通过式(4)将获得一个Toepliz 矩阵。把积分区域限制到来代替H可以减少很多的计算量。

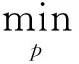
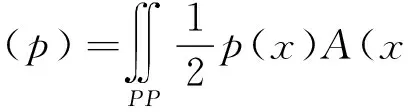
sub.p(x)≥0, ∀X∈H

(5)

对φ离散化，得到一个典型凸二次规划问题，由库恩-塔克最优条件，得到其线性互补问题。

1.2 离散化

为了解决这个问题的离散化，最方便的是用矩形H=[x1,xh]×[y1,yh]将潜在接触面离散化，分成n=mx·my个小矩形，每一个小矩形的尺寸为δx×δy。每一个元素可以通过二维指数(ix,iy)表示，也可以通过字典序号i=ix+(iy-1)·my表示。对每一个i，它决定了是属于接触区ε域还是外部区域。式(1)—(4)通过插入恒定的应力使得问题离散化，得到一个熟悉的凸规划：

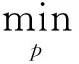
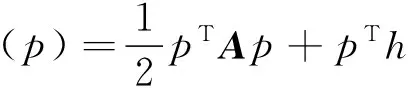
(6)

sub.pi≥0,i=1,…，n

(7)

由于是使用相等尺寸矩形离散化的，所以矩阵元素aij仅仅和xi-xj的相对位置有关，其中aij=cix-jx,iy-jy，矩阵A是由Toepliz块组成的矩阵，每一个Toepliz块的尺寸是mx×mx：

(8)

在二维接触问题中，mx=1或者my=1，此时矩阵A是Toepliz矩阵。影响系数ckx,ky一共应该有(2mx-1)×(2my-1)个，可以通过等式(4)，将单位p看作单位1，得到：

(9)

关于影响系数的分析表达可见参考文献Sainsot P(2011)[6]，也可以用高阶形状函数表示，在Dydo J R[7]中用的是双线形状函数，使用了基于FFT(Fast Fourier transform)的方法。

2 基于共轭梯度算法

2.1 NORM有效集算法

式(6)(7) 典型的解决方法是有效集算法和内点法，在接触力学中，前者似乎用得更多。有效集策略由解决一系列的简单优化问题组成，直到这一系列的优化问题给出式(6)的最优解。简单的形式是忽略式(7)约束，用等式替代。对任意一个点L∈Rn，如果满足式(7)的约束条件，就叫做可行点。对一个可行点，通过约束条件i∈{1,2，…,n}将约束分为有效约束和非有效约束，其中li=0称为有效约束。更关注的是未知量li，被分成常量和变量，得到一个自由集(L)={i|li>0}和约束集ε(L)={i|li=0}。一般的有效集算法如下：

0. 设置一个迭代计数m=1，由初始可行点得到自由集m和约束集εm=Hm，其中H为潜在接触面。

Ⅰ. 求递减问题式(10)的最小值解Lm:

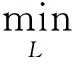
φ(L) sub.li=0, ∀i∈εm

(10)

Ⅱ. 如果对所有的i∈m，有li>0，且对所有的j∈εm，有≥0(两个接触面未变形的间隙)，即可得所求L，否则m=m+1，重新计算得m,εm，然后返回第Ⅰ步。子问题式(10)比最初的问题式(6)(7)有更简单的结构。对给定的自由集,式(10)可以写成下面的形式：

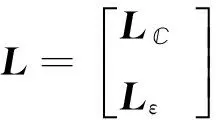
(11)

自由变量的编号是由约束变量获得的，引进矩阵Cm，矩阵Cm的元素来自矩阵L，h，其中i∈m，Cm是一个t×n的矩阵，t是接触域元素的个数，在这些构造下，式(10)的最小值Lm在对给定的的自由集m中,由子向量和构成：

A=CmA(Cm)T

(12)

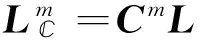
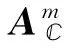
2.2 有约束的共轭梯度算法

有一些作者结合有效集策略和共轭梯度算法来解决弹性接触问题，这个可以不用求精确解，例如接触软件，用最大CG方法迭代20次，这个结果被称为NORM+CG(20)。

文献[10]的算法是通过Sainsot和Lubrecht略加改进所得，图2表明对一个粗糙的接触问题采用不同算法的收敛过程。

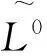
ε0={i∈H|li0=0∧ei0>0},0=Hε0

求最初接触区域和外部区域。

Ⅰ. 开始迭代k=1,2,…，对给定的k-1,εk-1,Lk-1和ek-1。

Ⅱ. 构造一个迭代方向vk，

(a) 对自由未知量的子问题，定义残差:

(b) 如果k=1或者kchg≥ksteep且k>kchg+3同时成立，则使用最速下降法重新开始CG算法，vk=rk-1,ksteep=k。

(c) 或者用Polak-Ribiere公式和共轭梯度构造搜索方向:

,rk-1-rk-2)/(rk-2,rk-2)

vk=rk-1+ max(0,

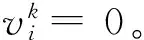
Ⅲ. 在不破坏约束条件下计算最优步长αk:

qk=Akvk,qεk=0

αPRk=(rk-1,Lk-1)/(vk,qk)，

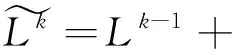
Ⅴ. 在内部循环的最后，执行约束条件检查和接触面积相应调整。

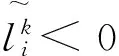
(b) 利用矩阵向量积ek=ALk+h计算得到ek。

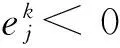
(d) 在第Ⅴ(a)或Ⅴ(b)步骤中，如果接触区域发生了改变，则令kchg=k。

3 数值结果

这部分针对粗糙的弹性接触问题举出不同算法和变体得到不同数值结果。测试的问题是两个无摩擦的光滑刚性平底圆形冲床之间的摩擦接触面(直径D= 8.97 mm)，是一个粗糙的，弹性半空间，参见图1。

两个接触面未变行时候的距离h是由接触面的高度z和渗透高度δz所给定的，添加上弹性变形系数u得出变形距离e=h+u，主要要求的问题是找到压力p满足如下条件：

∀X∈ε:e≥0,p=0

(13a)

∀X∈:e=0,p>0

(13b)

图2说明3种不同的方案，通过改变摩擦系数γ=0.5,0.8和0.95，每个方案δz也是变化的，以至于接触区域的元素个数为5%～65%。每次设定10个随机的接触表面，区域的尺寸是10 mm×10 mm，离散化有200×200个元素，大概有25 300个未知变量在环形冲床上，因此自由变量的个数是在1 250～16 450之间变化。这个方法测试的初始点为零或均匀分布在pmax·[-0.3,0.7)中,其中pmax是最大可行解。每个接触面有10个不同的初始点x0，一直迭代，直到接触面不再变化并且均方差根变化小于erei=10-6，例如：

(14)

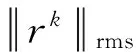
图1 弹性半空间Fig.1 Elastic halfspace

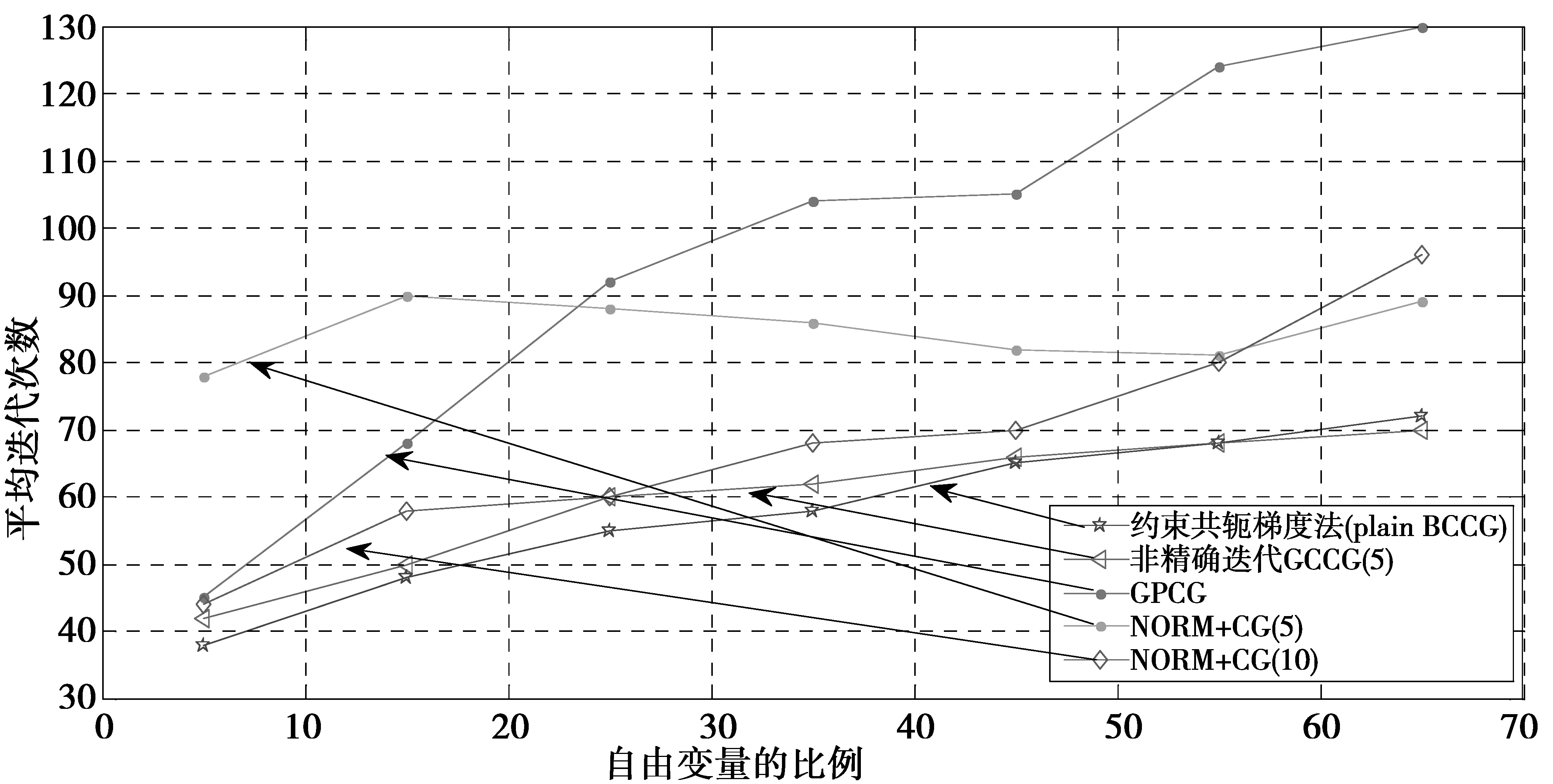
图2 不同算法的平均迭代次数Fig.2 Average number of iterations for different algorithms

结果表明，普通的BCCG(Bound-Constrained Conjugate Gradient method)算法随着自由变量的增加，迭代次数也随之增加，共轭梯度算法的效果降低了。在越来越多的步骤中，同一时刻被约束的变量越来越少，而且每次随着有效集的改变，共轭梯度算法都要重启。这个结果对NORM+CG(3)算法影响就比较小。对于γ=0.95，这个影响会显得更大，其中普通的BCCG算法会增加到190，然而c才增加到95，但对BPCG算法影响没那么大。进一步关于这个问题的测试结果在文献[10]中，其中表明，NORM+CG(20)算法比NORM+CG(∞)需要更多的外部迭代。

4 结 论

在解决有约束的凸二次规划问题时，不必苛求目标函数每一步迭代函数值都在递减，总体在下降就是好的结果，现存的有效集和基于共轭梯度算法的策略对解决凸二次规划问题给出了有效步的证明。预测这个收敛性也是成立的，并不一定要函数是持续递减，只要黑赛矩阵是非负矩阵就行。

提出的标准BCCG算法和增强BCCG(K)算法是用共轭梯度算法解决线性问题的延伸。主要体现在中间点迭代的时候，用Polak-Bibiere 公式代替了最速下降法，更有趣的一点是，通过对约束条件放宽，以及持续的共轭迭代，来代替共轭梯度算法的重启。数值结果表明：相比较GPCG算法，改进的算法的迭代次数下降了20%。除此之外，不用总是调试问题的参数。总之，增强的共轭梯度算法对弹性接触问题有很好的表现。

[1] HAGER W W,ZHANG H.A New Active Set Algorithm for Box Constrained Optimization[J].Siam Journal on Optimization,2006,17(2):526-557

[2] BERTSEKAS D P.Nonlinear Programming[M].Wiley,1983

[3] HESTENES M R,STIEFEL E.Methods of Conjugate Gradients for Solving Linear Systems[J].Journal of Research of the National Bureau of Standards,1952,49(6):409-436

[4] SHEWCHUK J R.An Introduction to the Conjugate Gradient Method Without the Agonizing Pain[M].Carnegie Mellon University,1994

[5] KALKER J J.Three-Dimensional Elastic Bodies in Rolling Contact[J].Journal of Applied Mechanics,1993,60(1):255-260

[6] SAINSOT P,LUBRECHT A A,SAINSOT P,et al.Efficient Solution of the Dry Contact of Rough Surfaces:a Comparison of Fast Fourier Transform and Multigrid Methods[J].Archive Proceedings of the Institution of Mechanical Engineers Part J Journal of Engineering Tribology 1994-1996,2011,225(225):441-448

[7] DYDO J R,BUSBY H R.Elasticity Solutions for Constant and Linearly Varying Loads Applied to a Rectangular Surface Patch on the Elastic Half-space[J].Journal of Elasticity,1995,38(2):153-163

[8] 赵礼阳,霍永亮.求二层线性规划最优解的极点方法[J].重庆工商大学学报(自然科学版),2015,32(11):89-92

ZHAO L Y,HUO Y L.The Method of Getting Extreme Point of the Optimal Solution to Bilevel Linear Programming[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2015,32(11):89-92

[9] POLONSKY I A,WKEER L M.A Numerical Method for Solving Rough Contact Problems Based on The Multi-level Multi-summation and Conjugate Gradient Techniques[J].Wear,1999,231(2):206-219

[10] VOLLEBREGT E A H.The Bound-Constrained Conjugate Gradient Method for Non-negative Matrices[J].Journal of Optimization Theory & Applications,2013,162(3):931-953

责任编辑：李翠薇

Conjugate Gradient Algorithm Based on Elastic Contact

YU Xiao-gang, DU Jun-huai
(School of Science, Nanjing University of Science and Technology, Jiangsu Nanjing 210094, China)

In order to solve constrained multiple iteration problem based on conjugate gradient for quadratic programming algorithm, by combining conjugate gradient algorithm and effective set strategy, this paper proposes a new algorithm model by truncating variables to avoid restarting conjugate gradient algorithm (by using Polak-Bibiere formula). In large scale elastic contact problems, a lot of results show that this algorithm is effective.

convex programming; condition constraint; conjugate gradient algorithm; effective set strategy; elastic contact problem

2016- 05-11;

2016-10-28．

余小刚 (1990-)，男，安徽安庆人，硕士，从事非线性最优化研究.

10.16055/j.issn.1672-058X.2017.0002.013

F224.7

A

1672-058X(2017)02-0060-05