等温容器充气时截面铜丝分布的拓扑优化研究
2017-03-27杨丽红刘晨中
杨丽红,刘晨中
(上海理工大学 机械工程学院,上海 200093)
等温容器充气时截面铜丝分布的拓扑优化研究
杨丽红,刘晨中
(上海理工大学 机械工程学院,上海 200093)
以等温容器截面为研究对象,截面铜丝看作多孔介质,采用拓扑优化方法优化铜丝分布,强化充气过程中容器中心向容器壁的导热。选用变密度法材料插值模型,基于弹性体结构拓扑优化模型和热力学知识,推导建立基于变密度法的散热体结构拓扑优化数学模型。以改进的网格灵敏度过滤技术等用于解决优化中的数值不稳定现象,运用Matlab编程得到容器截面铜丝分布的拓扑优化模型。并在初始温度20 ℃,中心边界200 ℃加热的情况下,经过200 s,通过与均匀填充和二层变密度填充模型的瞬态导热仿真对比,得出拓扑优化模型的导热效果更佳。研究结果表明,经过拓扑优化后的填充模型可强化等温容器充气过程中由中心向周围的传热。
等温容器;多孔介质;强化传热;拓扑优化;变密度法
等温容器概念是日本东京工业大学香川利春教授于1995年提出的,是一种在普通容器内填充一定量的等温材料(一般为细铜丝),使其无论在充气还是放气时容器内空气温度都基本不变的一种特殊容器[1]。由于其等温特性,常被用在气动系统的测试和控制中,尤其在流量测试领域得到了广泛的应用。利用等温容器用来检测气体流量计的动态性能[2-3];测定气动元件的流量特性[4];用于提高真空吸盘动态压力响应和组成高精度、快响应减压阀控制气动隔振台[5]等。但在等温容器实际应用过程中,由于充放气时容器内填充的金属丝强化传热效果不足,导致容器内气体温度存在偏差,致使容器的实际等温效果不够理想。为了使等温容器更好的适用于流量测试等领域,通过强化金属丝的传热效果来改善容器充气时的等温特性具有重要的研究价值。许多学者在研究细金属丝填充物强化传热时[2-4],将其看作是多孔介质。
拓扑优化是以材料分布为研究对象,在一块初始设计域内,通过拓扑优化,找到材料最佳的分布方案。目前主要的拓扑优化方法有均匀化方法、变密度法、渐进结构优化法和水平集方法。散热结构的优化设计是拓扑优化的一个重要的研究领域,在给定材料的约束下,找到结构最佳的传热路径。传统的传热结构设计一般是基于热力学计算和工程经验,然而不同拓扑结构形式散热器的散热效果显然不同,如何找到物体的最佳散热拓扑结构,是一个重要的问题。 Sigmund[7]将结构拓扑优化中的变密度法直接拓展到了传热结构优化中,并发表了一个简单有效的拓扑优化程序,可应用于一般力学和传热学结构当中。国内左孔天[8]应用结构力学中的SIMP法,建立了热传导结构的拓扑优化数学模型,说明在结构优化中广泛应用的拓扑优化方法,也可用来优化材料拓扑分布来强化传热。曹茹[9]基于渐进结构优化思想的优化方法和优化准则,建立了热传导结构的拓扑优化数学模型。
1 热传导结构拓扑优化数学模型建立
变密度法又称为固体各向同性材料惩罚法(Solid Isotropic Material with Penalization,SIMP),假定材料为各向同性材料,以材料密度为设计变量,无需加入附加的均匀化过程和细微结构,准确快捷地获取弹性模量与单元密度之间的关系,从而减少优化设计变量,简化优化求解过程,是一种应用广泛的材料插值方法。
在SIMP方法前提下,优化目标为最小柔度的弹性体结构拓扑优化数学模型为[7]
s.t.:V=f·V0
KU=F
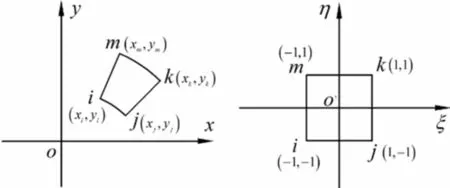
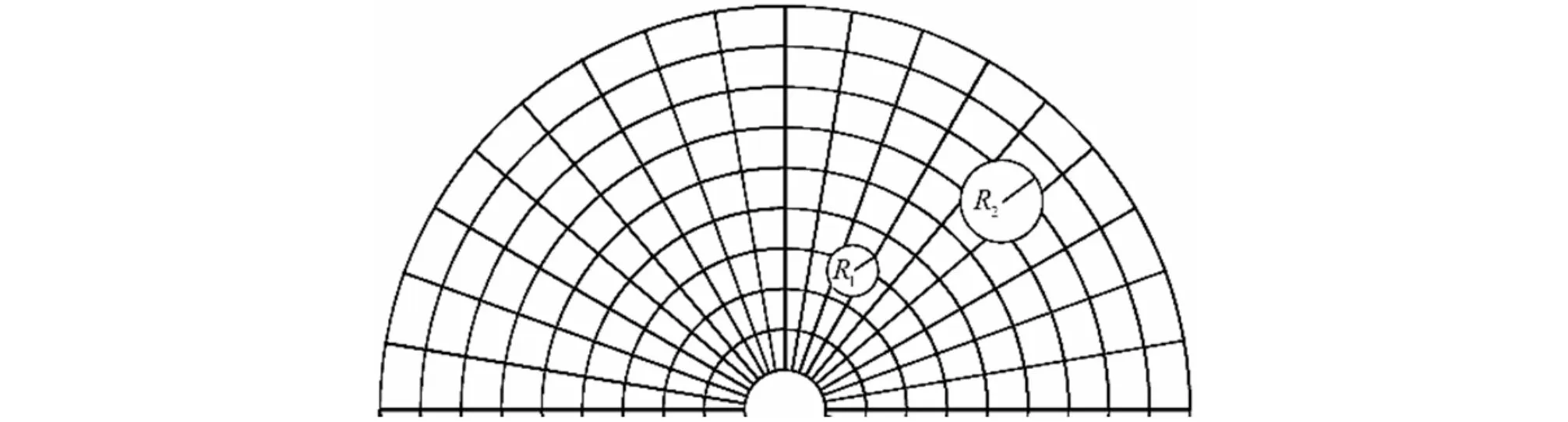
0 (1) 式中,U和F分别为位移列阵和力向量;K为整体刚度矩阵;V和V0为优化后结构体积和设计域初始体积;f为规定的体积比;xe为设计变量,以单元相对密度表示;xmin为设计变量的最小极限值;ue表示单元刚度矩阵;n为离散单元总数目。 ke=(xe)pk0,k0和ke分别表示初始刚度矩阵和优化后刚度矩阵, 为惩罚因子,其的作用是对中间密度单元项进行惩罚,使中间密度单元数目尽量减少,结构单元密度尽可能趋近于0或1。 对于平面导热,其导热微分方程为 (2) 式中,λ(W·m-1·℃-1)为材料的导热系数;ρ(kg·m-3)为材料密度;c(J·kg-1·℃-1)为材料的比热容;T(℃)为物体的瞬态温度;t(s)为导热时间;qv(W·m-3)为材料的内热源强度;x和x(m)为直角坐标。 对于平面稳态热传导有 (3) 边界条件:这里假定模型存在第一类边界,无第二类、第三类边界,所以 T|Γ=f(x,y,t) (4) 其中,Γ为物体边界;f(x,y,t)为已知温度函数。 初始条件:规定了开始传热时物体所具有的温度,公式表示为:T|t=0=φ(x,y)。 选择合适的目标函数是拓扑优化求解的至关重要的一步。对于稳态热传导问题,传入区域的热量为 (5) 在非稳态传热情况下,将各点温度与热流密度的乘积积分称为散热弱度。物体在内部和边界上传入的热量一定的条件下,温度越低,散热弱度越小,整个设计域上的平均温度越低。根据傅里叶定律将q的表达式带入可得到散热弱度 (6) 对于稳态情况,不考虑对流边界,去掉式(6)的后一项,然后经离散化处理后得 (7) 式(7)中,散热弱度的量纲是焦耳·开尔文(J·K),其代表物体向周围介质导热的能力。热量传递中散热弱度存在耗散,当其热量传递过程中散热弱度为最小时,热量传递效率最高。散热结构拓扑优化的目标就是使散热弱都最小化,最小散热弱度等于最大散热强度。 根据弹性体的拓扑优化模型,相应的可建立热传导结构的拓扑优化数学模型 s.t.:V=f·V0 KT=P 0 (8) 式中,K为结构总体热刚度矩阵;ke为单元热刚度矩阵;te为单元温度,T为由te组成的列向量;xe为单元相对密度;k0为材料密度为1的单元热刚度矩阵;P为节点热载荷列阵。 由于研究模型为单目标函数问题,优化算法选取优化准则法(OC),OC法具有程序设计量较低,对设计变量数没有太大要求,程序收敛快等优点。其是由目标函数和约束条件构成的拉格朗日函数。考虑设计变量上下限的情况,可推得式(8)的优化准则法求解公式为 (9) 引入阻尼系数 是为了确保数值计算的收敛性和稳定性。 2.1 单元热刚度矩阵 由于所研究的截面模型离散出的四节点四边形单元不是规则的四边形,图1所示,所以对于任意形状的四边形单元要寻求一种坐标变换转换为图1右图的正方形单元,将整体坐标 转换为局部坐标(ξ,η)。 图1 四边形单元坐标变换 构造四边形单元形函数和局部坐标温度插值函数。对于平面温度场的计算,运用四边形单元变分原理,可得到 (10) 其中,J为温度场泛函;[N]e{∂T/∂t}e为单元非稳态温度对时间的变化函数。对于稳态热传导,不考虑对流边界情况,公式可简化为 (11) 单元热刚度矩阵的求解运用二维高斯数值积分即可得出。 2.2 实现流程 变量的迭代更新,采用OC优化准则法迭代,利用Sigmund提出的著名启发式迭代格式对变量进行迭代更新,选择移动变量m=0.2,表达式为 (12) 在SIMP材料插值模型的基础上,基于OC优化准则算法求解散热结构拓扑优化问题的实现流程如图2所示。 图2 基于SIMP法的散热结构拓扑优化流程图 2.3 数值不稳定现象及解决方法 拓扑优化中常出现数值不稳定现象:多孔材料、棋盘格、网格依赖性和局部最优等。多孔材料问题前面通过在目标函数中添加惩罚因子p的方式来尽量消除。针对棋盘格和网格依赖性现象,本研究采用Sigmund[7]提出的灵敏度过滤技术,选用线性过滤中基于卷积技术的灵敏度过滤技术。过滤器通过对第e个单元的灵敏度和其周围的单元灵敏度进行加权平均以防止密度的突变,虽该方法是启发式算法,但由于过滤方法无需考虑额外的约束,没有增加优化问题的复杂性。 e=1,2,…,n (13) 图3 不同过滤半径的影响效果示意图 2.4 优化结果 本文根据等温容器截面铜丝的形状,建立了内径20 mm,外径200 mm的圆环状模型,网格划分为40×160个单元。使用Matlab进行有限元分析、热刚度矩阵、拓扑优化等程序的编辑,阻尼系数η取 ,惩罚因子p取3,式(8)中体积比f取30%,程序运行迭代得到优化后的模型。 最终的优化结果得到了预想中的树枝状结构。几个主枝干集中在靠近容器中心的部位,越向外分支越多,浅色部分代表设计变量密度小的区域,深色部分代表密度大的区域。 为验证优化模型的强化传热效果,对模型进行非稳态导热仿真分析。有些学者[14]研究表明多孔介质内层孔隙率小,外层孔隙率大的分层变密度填充可有效增强强化传热效果。容器分层填充热量传导过程可看作多层同心圆环的传热,本文采用优化模型与均匀填充和二层变密度填充进行对比的方式验证拓扑优化的优化效果。 截面铜丝看作大孔隙率多孔介质,为保证每个模型所用到的铜丝质量相同,均匀填充模型的孔隙率设定为97%,二层填充以划分网格的第20层,即半径55 mm处为分界,半径10~55 mm圆环部分的孔隙率设为93.42%,55~100 mm圆环部分孔隙率设为98.5%,拓扑优化模型中设计变量密度大的单元采用较小的孔隙率,密度小的单元采用较大的孔隙率,使其整体平均孔隙率基本保持在97%。 有限元热传导模型:{P}t=[K]t{T}t+[N]{∂T/∂t}t,其中总体热刚度矩阵K由上文中得出的单元热刚度矩阵组装得到:[K]=∑[Ke];[N]{∂T/∂t}t为非稳态温度对时间的变化函数,矩阵N可由矩阵K的求解方法得出;温度时间导数{∂T/∂t}t采用向后差分的格式变换:{∂T/∂t}t=({T}t-{T}t-Δt)+O(Δt),Δt为时间差分步长,O(Δt)表示截断误差的数量级。 矩阵中所用到的导热系数、密度和比热容需按照孔隙率的大小进行变换 λe=(1-φ)λs+φλf ρe=(1-φ)ρs+φρf ce=(1-φ)cs+φcf (14) 式中,φ为孔隙率;λe、ρe、ce分别为有效导热系数、有效密度和有效比热容;λs、ρs、cs为纯铜的相应参数;λf、ρe、ce为20 ℃时空气的相应参数。 仿真初始温度设为20 ℃,内边界温度为200 ℃,导热时间200 s,Matlab编辑仿真程序,得到优化后模型的温度场分布图。 图5 优化模型温度分布图 对均匀填充在相同条件下仿真后得到温度场分布图。对二层填充在相同条件下仿真后得到温度场分布图。 图6 均匀填充温度分布图 图7 二层变密度填充温度分布图 为更直观对比3种填充模型的温度分布,按照半径上40层层数为横坐标,每层160个单元的温度取平均值作为纵坐标,绘制出如下的坐标图。 图8 优化后与均匀填充模型温度分布对比图 从对比图可看出,拓扑优化模型和二层变密度填充的导热效果要远远优于均匀填充,不仅温度分布更加均匀,且相同径向距离的温度值都要高于均匀填充,而拓扑优化模型还要略优于二层变密度填充。统计整体设计域的平均温度值,均匀填充的设计域平均温度为109.88 ℃,二层变密度填充为145.38 ℃,拓扑优化模型为150.64 ℃,拓扑优化模型设计域平均温度相较均匀填充高出37.1%,相较二层变密度填充高出3.62%。即在相同传热时间内,拓扑优化模型缩小了容器壁与容器中心的温差,提高了容器截面的导热效率,达到了强化传热的目的。 等温容器广泛地应用于气动系统等领域中,为更好地利用和改善其等温特性,优化容器截面铜丝的分布,增强其强化传热效果具有重要的研究意义。 (1)本文将已经被广泛应用的基于SIMP法的弹性体结构拓扑优化方法与热力学知识相结合,推导得出基于SIMP法的散热体结构拓扑优化数学模型;(2)求解得出了不规则四边形单元的热刚度矩阵,改进的网格灵敏度过滤技术和惩罚因子的引入基本解决了优化过程中的数值不稳定现象,然后使用Matlab编程得出拓扑优化结果;(3)在平均孔隙率一致的情况下,将拓扑优化模型与均匀填充和二层变密度填充进行瞬态导热仿真分 析的对比,仿真结果表明拓扑优化模型的强化传热效果要优于另外两种模型,其整体设计域的平均温度较均匀填充高出37.1%,较二层变密度填充高出3.62%。 以上研究结果表明拓扑优化方法可应用于传热问题当中,最终的优化模型降低了等温容器充气时中心与容器壁的温差,达到了强化传热效果。得到的优化模型也可应用于电子电路的散热问题当中。 [1] 蔡茂林.现代气动技术理论与实践第九讲:等温容器[J].液压气动与密封,2008,28(4):90-93. [2] Kawashima K,Kagama T.Unsteady flow generator for gases using an isothermal chamber[J].Measurement,2003,33(4):333-340. [3] Funaki T,Kawashima K,Yamazaki S.Gener-etor of variable gas flows using an isothermal chamber[J].Measurement Scie-nce and Technology,2007,18(3):835-842. [4] Kawashima K,Kagama T,Funaki T.Instant-aneous flow rate measurement of ideal gases[J].Journal of Dynamic Systems,Measurement,and Control,2000,122(1):174-178. [5] Kato T,Kawashima K,Funaki T. A new,high precision,quick response pressure regulator for active control of pneumatic vibration isolation tables [J].Precision Engineering,2010,34(1):43-48. [6] 杨丽红,孙金祥,沈航明.变密度多孔介质强化导热模型及实验研究[J].热能动力工程,2014,29(5):515-520. [7] Bendsoe M P,Sigmund O.Topology optimization:theory,methods,and application [M].New York:Springer,2003. [8] 左孔天,陈立平,张云清,等.用拓扑优化方法进行热传导散热体的结构优化设计[J].机械工程学报,2005,41(4):13-16. [9] 曹茹,陈登平.基于ESO法的热传导结构拓扑优化设计[J].兰州交通大学学报,2011,30(4):86-89. [10] 孙祥谦.有限单元法在传热学中的应用[M].3版.北京:科学出版社,1998. [11] 程新广,李志信,过增元.基于最小热量传递势容耗散原理的导热优化[J].工程热物理学报,2003,24(1):94-96. [12] 杨丽红,沈航明,宋元明.等温容器放气过程中对流换热模型的研究[J].中国机械工程,2014(18):2489-2495. [13] Rocha Lao,Lorente S,Bejan A.Constructal design for cooling a disc-shaped area by conduction[J].Heat Mass Transfer,2002,45(8):1643-1652. [14] 刘伟,明廷臻.管内核心流分层填充多孔介质的传热强化分析[J].中国电机工程学,2008,28(32):66-71. [15] 陈文炯,刘书田,张永存.基于拓扑优化的自发热体冷却用植入式导热路径设计方法[J].力学学报,2016,48(2):406-412. Study on Topology Optimization for the Copper Wire Distribution of Isothermal Chamber Section During Inflating YANG Lihong,LIU Chenzhong (School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093, China) With isothermal chamber section as the research object,the copper wire section is considered porous media,optimizing the distribution of copper wire with topology optimization to strengthen conduction of the chamber center to the chamber wall during inflating.Above all,selecting the variable density method interpolation model,setting up heat dissipation structure topology optimization mathematical model based on the variable density method by the elastic body structure topology optimization model and the knowledge of thermodynamics.Secondly,the improved mesh sensitivity filtering technology is used to solve the numerical instability phenomenon of optimization,topology optimization model of the copper wire distribution of chamber section can be gotten by using Matlab programming.Finally,on the condition of the initial temperature of 20 ℃,heating center boundary of 200 ℃ and through 200 s,heat conduction effect of topology optimization model is better by contrast of transient simulation of thermal conductivity with uniform filling and filling model of two-layer variable density.Research results show that the topology optimization filling model can be used to strengthen the heat conduction from the center to the surrounding of isothermal chamber during inflating. isothermal chamber; porous media; heat transfer enhancement; topology optimization; variable density method 2016- 04- 22 国家自然科学基金资助项目(51245009);上海市自然科学基金资助项目(12ZR1420600) 杨丽红(1973-),女,博士,副教授。研究方向:先进制造技术等。刘晨中(1991-),男,硕士研究生。研究方向:传热传质优化。 10.16180/j.cnki.issn1007-7820.2017.03.018 TN304;TP301.6 A 1007-7820(2017)03-065-05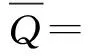

2 优化的实现流程与结果


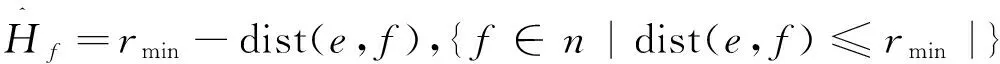


3 仿真分析




4 结束语
