基于遗传算法的信号灯配时
2017-03-27万善余
万善余,范 迪
(上海理工大学 交通系统工程系,上海 200093)
基于遗传算法的信号灯配时
万善余,范 迪
(上海理工大学 交通系统工程系,上海 200093)
传统的信号灯配时主要以车辆延误作为评判标准,而忽略作为交通主体的乘客。环境污染日趋严重,交叉口配时亦应考虑车辆滞行造成的超量尾气排放。因此,文中考虑乘客因延误而损失的时间价值及交叉口车辆尾气排放造成的污染损失,重新设计信号灯配时方案。采用双层规划模型进行信号灯配时,以遗传算法求解。上层模型目标为乘客经济损失最小,下层则为尾气排放最少。提出的配时模型的目标函数经检验不是正相关,所以均为有效目标函数。不同交通构成情况下的仿真结果显示,文中模型能使乘客经济损失和汽车尾气排放均降低约30%。
遗传算法;双层规划;信号配时;时间价值;尾气排放
随着汽车数量逐年增长,交通拥堵日渐严重。每年全国因交通拥堵所造成的损失达上亿元,报告[1]指出北京的拥堵经济成本为335.6元/月。因此,交通系统设计有必要考虑交通系统的经济损失。
交通信号灯控制最早由英国学者Webster于1965年提出[2],之后诸多学者完善和改进信号灯配时设计,其工作主要集中在模型参数的修正[3],常云涛[4]提出基于乘客平均延误的配时方案,考虑了车辆载客率不同情况下人的总延误,有效改进了模型。这体现了作为交通主题的人本位思想。人均延误和车辆延误有时无法兼顾,如果仅考虑人均延误,那么有可能引起车辆延误增大、车辆尾气排放增大等一系列不良影响。而通过考虑不同目标,提出多目标规划[5],引入多个目标函数,求解得到的新的配时方案可使系统实现多目标平衡优化。同时还有众多研究信号配时方案,并提出了多种思路,主要集中在公交优先以及不同交通状况下的信号灯配时方案设计[6]。
目前,信号灯配时研究主要集中在乘客延误、汽车尾气排放、停车次数和车辆总延误这些目标函数上[7],但针对单个交叉口都未考虑不同出行方式乘客时间价值的不同以及整个交叉口的经济损失。随着环境问题的日益增加,汽车尾气污染越来越受到人们重视,同时人的健康问题日趋严重,所以信号交叉口配时也应该考虑使汽车在信号交叉口尽可能少排放尾气。因此,上述研究得出的结果能使得延误减小,但整个交叉口的经济损失未必最小。本文针对以往研究的缺陷,以单个交叉口的整体经济损失最小和尾气排放最小为目标,进而优化单个交叉口的信号配时。这样不仅体现了行人在交通中的主体地位,同时也是对社会公平性的权衡。本文中各参数含义如表1所示。

表1 参数定义
1 交叉口延误模型
1945年Webster首次提出延误计算公式[8],在饱和度<1的情况下,Webster公式具有良好的适应性
(1)
本文目标函数不仅考虑乘客的时间价值,使单个交叉口的经济损失最小,同时也考虑汽车尾气的排放,使汽车的尾气排放最小。本文采取一个双层规划模型设计信号交叉口配时方案。上层模型以单个交叉口社会效益最优为目标函数,下层模型以单个交叉口汽车尾气排放最少为目标函数。
2 模型的建立
2.1 上层价值损失最小模型的建立
上层模型主要考虑整个交叉口总的经济损失最少,因此用车辆的经济损失加上行人的经济损失。车辆各个方向上的延误以不同乘客时间价值和人数的乘积得出
minc=cv+cp
(2)
(3)
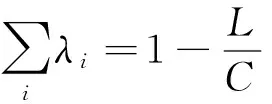
其中,第1项约束为每个方向上的绿信比均≤1;第2项是周期时长的约束必须小于最大周期而且大于最小周期;第3项为绿信比的约束;第4项是绿信比之和必须等于1减去周期损失时间比
(4)
由于早高峰时期乘客的时间价值含有必要的惩罚成本,所以时间价值可分为早高峰时间价值与平峰时间价值
(5)
ξ为时间价值迟到惩罚系数,主要针对早高峰上班人群中,由于早高峰如果迟到则此时时间价值会远远超过普通时间的时间价值,因此有必要考虑此时的时间价值影响。
2.2 下层尾气排放模型的建立
(6)

参数的标定可根据文献[9]将所考虑路段不同速度下的状况进行拟合求得EF
(7)
EFIpcu交叉口处排队等待时的CO 怠速排放因子为0.1817 g/PCU·s。
3 模型的求解
目前求解双层规划的算法较多,众多启发式算法均较为有效[10]。由于遗传算法具有良好的适应性,不要求目标函数在可行域上可微,所以解决交通控制类问题不仅有效果且效率较高。本文主要采用遗传算法对该双层规划问题求解。
(1)首先确定适应度函数,由于本问题为双层规划,因此需要确定两个适应度函数。其中第一个一个为总共时间价值的适应度函数,第二个为总共尾气排放的适应度函数;
(2)设置基本约束,本问题即是每个方向上绿灯时长的约束以及信号周期时常的约束。即每个方向上绿灯时间范围[10,90]周期时长范围[90,240];
(3)设置遗传算法的基本参数,包括种群规模15、交叉率80%、最大迭代次数200等;
(4)随机产生与约束相符合的初始种群。计算每一个个体对目标函数的适应度;
(5)交叉变异运算产生子代,变量离散化,进行计算;
(6)判断是否达到误差标准与迭代次数限制,若是则执行下一步, 否则返回步骤(5);
(7)根据目标函数值计算出最优解, 即一个周期内每个相位的绿灯时间。然后根据每个相位绿灯时间最后算出周期时长。
4 实例分析
根据上海地区的平均现状和实际路况,取四平路大连西路的一个交叉口调查晚高峰时期交通量,然后根据双层规划配时。
信号灯配时现状:信号周期时长为210 s共有4个相位。东西向直行95 s 左转35 s,南北向直行35 s左转45 s。交通量如表2所示。

表2 各个进口道小时交通量 /pcu/h
公路单车道通行能力可参考文献[11]取1 800 pcu/h。平均载客率经调查可得小客车2.5人、大客车15人、小货车1.5人、大货车1.5人、公交50人。根据问卷调查可以得出各种出行方式在此时段的价值,最后计算结果如表3所示。

表3 各种出行方式对应时间价值表
由于尾气排放模型第一项与配时方案不相关,而第二项与配时方案有关,所以计算时只以第二项为尾气排放可变项,并作对比,加大计算效率。最后用Matlab计算的出入口现状配时情况下高峰小时因延误而产生的损失为12 636元,尾气排放可变项为结果为601。用遗传算法优化后的配时方案为信号周期时长为107 s共有4个相位。东西向直行51 s 左转11 s,南北向直行24 s,左转21 s。此时的经济损失为8 080元,尾气可变项的结果为394。
对比优化前后结果可看出,本文采用的模型配时方案能有效的减少经济损失和尾气排放。其中,经济损失减少了原来的36%,尾气排放可变项降低了34%。因此模型针对单个交叉口信号配时优化具有良好的适应性。
5 模型分析
5.1 双目标的有效性
对于双层规划的上下层模型若呈现正相关,则表明模型的目标函数只有一个有效。因此,检验双目标模型的有效性在双层规划中非常有必要。为了检验模型的有效性,将交通流只分为公交车与其他车辆[12-16]。此处其他车辆的时间价值采用加权平均求得
(8)
假设公交车占车流的不同比例,优化后对比前后经济损失和尾气可变项的变化。最后结果如图1所示。

图1 目标函数相关性图
由结果可看出,显然两个目标函数不是正相关,所以两个目标函数对于单个交叉口均为有效目标函数。模型具有良好的适应性。
5.2 参数有效性分析
本文有效性分析主要考虑公交车在交通流中的比例对总成本的减少,将模型简化,简化方法与目标函数有效性简化一致。不同公交比例情况下经济损失的降低和尾气排放可变项降低绝对值和降低比例的变化,如图2所示。

图2 目标函数降低绝对值图

图3 目标函数降低比例图
由图2和图3可看出,不同交通构成情况下经济损失减少的绝对值不断增大,而尾气可变项在约为190波动。两个目标函数降低比例基本在约为30%波动,且在公交车比例达到40%时降低比例最大。因此模型基本稳定。
综上所述,本模型能够降低经济损失约30%,且在不同交通构成下模型均有效。由此可知,本模型在实际交通流构成不同的信号控制路口亦有效。
6 结束语
本文研究了单点交叉口信号配时问题,建立一个双层规划信号灯配时模型,并用遗传算法进行求解,利用实例对模型的有效性及适用性进行分析验证。得出结论:(1)经分析,经济损失和汽车尾气排放是两个有效的目标函数。不同交通构成下,模型均能使经济损失和尾气排放降低约30%;(2)本文只考虑单个交叉口信号配时,未考虑道路干线协调控制,因此本模型的在协调控制下的适应性有待探究。
[1] 任兴洲,王微,等.经济结构优化调整中着力促进服务业发展的制度环境研究[J].经济研究参考,2011(40):42-44.
[2] 尹宏斌,徐建闽.道路交通控制技术[M].广州:华南理工大学出版社,2000.
[3] 马万经,吴明敏,韩宝新,等.考虑可变速度调节的单点交叉口公交信号优先控制方法[J].中国公路学报,2013,26(2):127-133.
[4] 常云涛.基于乘客延误的信号交叉口配时优化模型[J].湖南大学学报:自然科学版,2009,36(9):22-26.
[5] Zegeye S K, De Schutter B, Hellendoorn J, et al. A predictive traffic controller for sustainable mobility using parameterized control policies[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(13):1420-1429.
[6] 王秋平,谭学龙,张生瑞.城市单点交叉口信号配时优化[J].交通运输工程学报,2006,6(2):60-64.
[7] 许智.混合交通条件下信号交叉口配时优化方法研究[D].北京:北京交通大学,2008.
[8] 高海军,陈德望,陈龙.混合交通流环境下信号配时研究[J].公路交通科技,2003,20(4):80-83,91.
[9] 陈群,晏克非.考虑公交优先的城市交叉口遗传算法信号配时研究[J].系统工程理论与实践,2005,25(11):133-138.
[10] 张萌萌,贾磊,邹难,等.单点交叉口鲁棒优化信号配时研究[J].公路交通科技,2011,28(1):107-111.
[11] 树爱兵.信号交叉口渠化与信号配时协调优化研究综述[J].中国公共安全:学术版,2010(4):78-82.
[12] 蒲琪,黄启超,杨佩昆.交叉口延误的概率统计模型[J].同济大学学报:自然科学版,2005,33(10):1309-1312.
[13] 王炜,项乔君,李铁柱.城市交通系统能源消耗与环境影响分析方法[M].北京:科学出版社,2003.
[14] 吴龙,任红民,毕惟红.遗传算法求解非线性方程组研究综述[J].电子科技,2014,27(4):173-178.
[15] 柏建普,吴强.蚁群混合遗传算法的研究及应用[J]. 电子科技,2011,24(4):20-23.
[16] 中华人民共和国交通部.公路工程技术标准JTG B01-2003[S].北京:中华人民共和国交通部,2004.
Traffic Signal Timing Based on Genetic Algorithm
WAN Shanyu,FAN Di
(Department of Transportation Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)
The traditional signal timing is based on the vehicle delay rather than passengers’s delay. At the same time, the environmental pollution is more and more serious, traffic timing should also consider vehicle emissions in the intersection. So in this paper, we consider the loss time value of passengers by delay and as well as the emissionvehicle exhausted in the intersection and redesigning the signal timing scheme. This article mainly uses the signal timing bi-level programming model, using genetic algorithm to solve at the same time.The objective of upper model isminimize economic loss, the lower model is minimize emissions. Upon examinationwiththe objective functionofthe model isproposed in this paperis notpositively correlated, so the objective functionare valid. In different circumstances of traffic simulation shows that this model can reduce the economic loss of about 30%. And vehicle emissions reduced by about 30%. So this model can applicable in different traffic conditions.
genetic algorithm; bi-level programming; signal timing; the time value; emissions
2016- 04- 22
万善余(1992-),男,硕士研究生。研究方向:交通仿真等。范迪(1990-),男,硕士研究生。研究方向:系统仿真等。
10.16180/j.cnki.issn1007-7820.2017.03.014
TTN911.73; U491
A
1007-7820(2017)03-049-04
