基于改进遗传算法的智能排课研究

2017-03-26王海波

电脑与电信 2017年12期

王海波

（南通科技职业学院，江苏南通 226007）

1 引言

当前，随着全国各高校的扩招及合并，使得学生在数量上激增，同时也增加了很多班级和专业。那么，伴随人工智能技术的发展，智能排课技术的研究已经成为高校信息化建设改革的热点。科学地编排课表可以稳定教学秩序，提高教学效率及质量，因此对智能排课技术的研究势在必行。

2 智能排课模型构建

在高校的教学过程中，主要有理论教学、实验教学、课内实践、课外实践、实习教学等。在课程的设置上有公共课、专业基础课、专业技能课等。那么，如何使得高校有限的教室、实验室及教师这些资源得以合理高效地分配和调度，是智能排课需研究的首要问题。

2.1 模型描述

高校的排课需考虑的要素有：班级，课程，时间，教师，教室。基本原则是：在同一时间段内，教师、学生和教室没有冲突，同时又要保证这些教学资源能够高效、合理被使用、分配。这里，针对高校智能排课，我们来构建其数学模型。

高校排课问题的解是周课时表，我们设某高校有M个班级，M={mm︱m=1,2,3…M}，其中每个班级的人数分别为{km︱m=1,2,3…M}；该校的课程总数是U，U={uu︱u=1,2,3…U}；每周从周一到周五上课，设连续两节课为一时间片，这样每天有4个时间片可以上课。每周可以有20个时间片。可以将这些时间片表示为：n1,n2,n3,……,n19,n20。共有R名专兼职教师，则 R={rr︱r=1,2,3…R}；且有T 个教室，T={tt︱t=1,2,3…T}，每个教室能够容纳学生的人数分别为{xt︱t=1,2,3…T}；那么在时间片nn，教师rr在教室tt中给班级mm教授uu课程，则nnrrttmmuu=1，反之nnrrttmmuu=0。

2.2 模型中约束条件

硬约束条件：

(1)在某教室上课的班级，其学生人数应小于或等于该教室所能容纳的最大人数，即km<=xt。

(2)在同一个时间内，同一行政班最多只允许安排一门课程，即

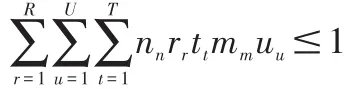
(3)在同一个时间内，同一教师最多只允许安排一门课程，即

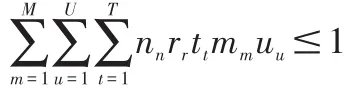
(4)在同一个时间内，同一教室最多只允许安排一门课程，即

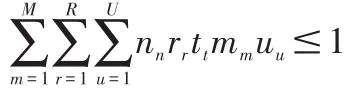
软约束条件：

软约束条件是指为了达到较好的教学效果，让课程的安排满足科学合理的要求，现考虑如下几项原则：

(1)教师在同一天内相邻时间片内的课程所安排的教室要尽可能相同或相近。

(2)学生在同一天内相邻时间片内的课程所排教室要尽可能相同或相近。

(3)同一行政班的同一门课每周安排两次，两次课之间的时间间隔要合理，最好相隔两天。均匀分配每班每天的课时总数。

(4)满足教师对教室及时间的一些特殊要求。

(5)针对不同课程的特点，合理安排上课的时间及教室，以达到最佳教学效果。

(6)在安排教室时，尽量达到教室所能容纳的最多人数与班级人数相匹配，达到最大化地利用教室资源。

2.3 模型的优化

智能排课就是如何将上述软约束条件进行最优组合的问题，我们设函数为f。

(1)对于有特殊要求的教师，优先安排好其上课地点及时间，依据教授、副教授、讲师这些职称来设相应权值ai(i=1,2,3)，相应的值为2、1、1。 f1=∑ai。

(2)如果某天的课时总数多于平均课时数的30%，其权值设为2，否则设为10。设相应权值di，则 f2=∑di。

(3)周学时多的课程要均匀合理分配，每周4学时的课也要均匀合理分配，设分配权值为yi，则 f3=∑yi。

(4)针对课程类型做合理划分，可分为：记忆理解型、推理逻辑型、操作实践型、综合型、体育类这五类。为每一类设定一个分值ei，则 f4=∑ei。

(5)设某行政班mm在某教室tt上课，该班上课的人数km与该教室能够容纳的最大人数xt的比值同教室的利用率成正比。则

通过上述对排课问题的分析讨论，得到目标的优化函数：

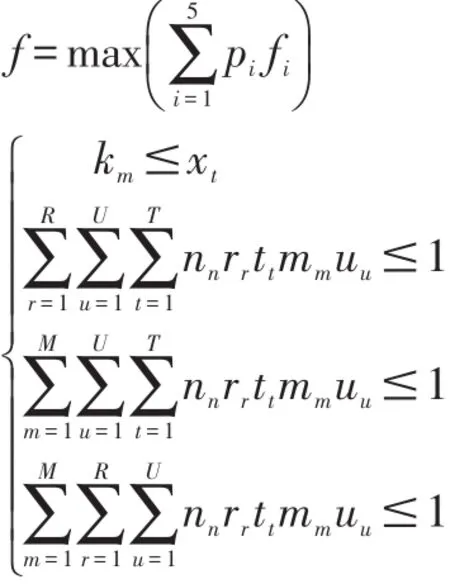
其中，pi(i=1,2,3,4,5)为约束条件权值，可以由工作人员根据经验来确定，这里，我们令 pi(i=1,2,3,4,5)的值分别为

3，9，6，4，5。

3 基于改进遗传算法的排课

3.1 遗传算法

遗传算法是一种随机搜索算法，通过对生物进化过程的模仿，在种群中的个体之间的重组、交叉和变异等遗传操作算子来实现优胜劣汰，进而完成搜索。遗传算法的基本运算过程为初始化，个体评价，选择运算，交叉运算，变异运算，得到下一代种群，终止条件判断。

3.2 遗传算法存在的缺陷及改进

(1)初始种群的均匀化改进

在一些遗传算法中，往往是随机产生初始种群，这就使得在解空间中初始种群的分布可能不均匀，进而算法的性能受到影响。所以，我们在初始种群产生时，就尽量使其在解空间中满足均匀分布。即，针对初始种群中的每个个体，为其设定一个限制距离，这样，初始种群中的每个个体之间的距离需大于这个距离限制，因而保证了在初始种群的个体在解空间中较均匀地分布，个体间有显著的差别，使得初始种群的模式丰富，进而得到最优收敛的全局解，使算法的性能得到提高。

(2)适应度函数的改进

在遗传算法中，适应度函数的选取非常重要，若选取不合理，可能会出现下述问题：

在遗传算法的应用前期，一些超常个体可能会出现，其有较强的竞争力，那么选择操控过程可能会依据概率选择法来进行，进而对算法的全局优化性能产生影响。

在遗传算法的应用后期，当种群个体间的适应度值差异较小时，其会接近收敛状态，这使得种群的优化潜能被降低，从而得到的算法最优解可能是局部的。

因此，适应度函数是否合理选取，对算法的收敛速度及能否得到最优解影响较大。

适应度函数需满足如下条件：

fitness(f(x))为适应度函数；

fitness(f(x))是一个是非负的连续的实函数，对是否可导无要求；

fitness(f(x))内的每个点与之相匹配的适应度值和染色体的好坏成反比；

fitness(f(x))函数不要复杂，简单为好；

fitness(f(x))函数要满足通用性，尽量参数少些。

所以我们给出适应度函数的定义：

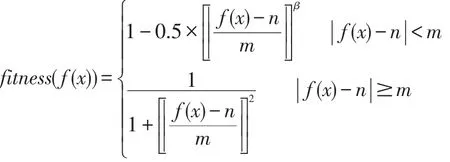
当 β=1时，fitness(f(x))在[0.5，1]是线性的；当 β=0.5时，可使得在算法的后期，有效拉开最优解附近点的适应度值，可以让我们更有效地做出选择。当β=1.5时，可使得在算法的早期，有效拉近最优解附近点的适应度值，这样算法就可以较快搜索到最优解区域。

对于m，将其调小，就可使fitness(f(x))函数的曲线变陡，将其调大，则可使fitness(f(x))函数的曲线变缓。这里，可以将n设为当代的最小值，它随遗传算法的进化而改变。

(3)变异算子的改进

在遗传算法搜索最优解的质量和收敛性方面，变异和交叉算子起到了决定性的作用。通常，遗传算法中交叉概率的选取很盲目，变异算子在寻优过程中，可以有效阻止过早的收敛。这里，我们对一些基因进行变异操作。

在当代群体中，对个体适应度较小的部分基因（约占90%左右），首先优化变量，然后再迭代计算，随着迭代数目的增加，每次得到的值也不停地发生改变，逐渐接近最优解。

变异操作的改进，能够产生比另外10%适应度基因更好的基因，这样算法的搜索解空间变小，寻优速度变快，进而解决了原来遗传算法的早熟问题和易陷入局部最优解的问题，且遗传算法的进化代数也可相应减少，更早得到最优解。

3.3 智能排课改进遗传算法流程

智能排课改进遗传算法流程图如图1所示。

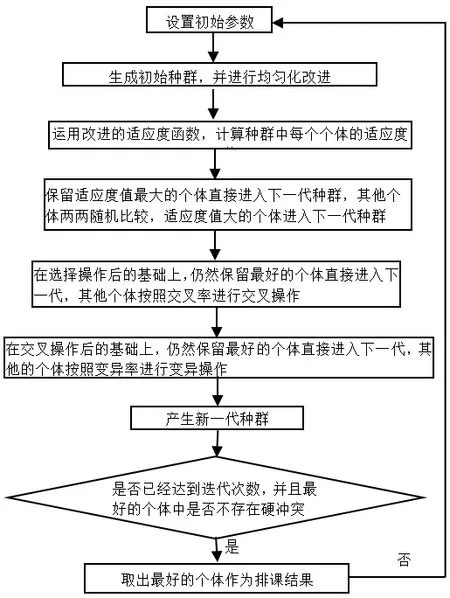
图1 智能排课改进遗传算法流程

3.4 算法的实现与分析

通过对以上遗传算法的改进，我们将其应用到智能排课问题上，实验使用Matlab R2010对使用遗传算法TGA和改进后的遗传算法IGA进行编程，在内存4.0GB，CPU 3.8GHz的电脑上运行。以某高校信息工程学院2016-2017学年下学期的排课数据作为测试，种群数设为120，实验考察算法的平均运行时间及算法较优解出现的次数这两个指标。

实验结果：

在排课方案应用两种算法，假设我们采用同样的方法确定两种算法的适应度函数，设迭代的次数分别为60，120，180，240，300，330，360，每次进行60次进行测试，记录运行结果，如图2、图3所示。

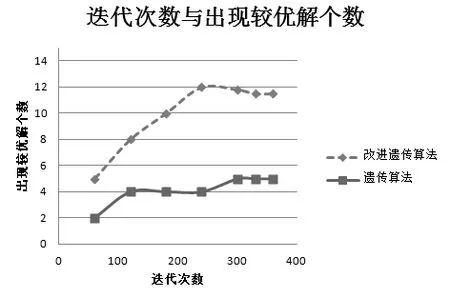
图2 TGA和IGA迭代数目与平均较优解个数

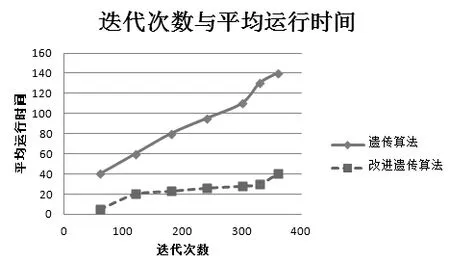
图3TGA和IGA迭代数目与平均运行时间

这里我们首先从出现较优解的数目分析，当迭代数目逐渐增加时，IGA和TGA两种算法出现较优解的数目都是逐渐趋于稳定的，但当我们固定迭代次数，IGA明显优于TGA，在数据上看，出现较优解的个数IGA要高出TGA两倍多。其次，我们来分析算法的收敛速度，当TGA出现较优解达到平稳时，所需时间较多，而IGA出现较优解趋于平稳时，所需时间较少，由此，对改进遗传算法的收敛速度比遗传算法的收敛速度明显高很多。

通过上述分析，本文中采用的IGA改进遗传算法具有收敛速度较快、易趋于全局最优解等特点。这源于：其一，IGA适应度函数的改进；其二，初始种群的均匀化改进，使得IGA的初始种群比TGA质量优秀；其三，IGA变异算子的改进及优化操作有效加速了后代个体的收敛性。