下凹内孤立波致流场结构及其影响因素的实验研究

2017-03-26武军林徐峻楠

海洋科学 2017年9期

武军林, 魏岗, 杜辉, 徐峻楠

武军林, 魏岗, 杜辉, 徐峻楠

(国防科技大学气象海洋学院, 江苏南京 211101)

为进一步探究海洋内孤立波诱导流场对海洋工程结构物以及潜航器的影响, 本文采用重力塌陷方法和粒子图像测速(Particle Image velocimetry, PIV)技术在大型分层流水槽中进行内孤立波造波以及内部流速场测量, 定量分析了下凹型内孤立波诱导流场结构及其影响因素。研究表明: 在密度分层流体中, PIV技术可实现对大幅面内孤立波诱导流场的精细测量以及波动结构特征的准确描述; 水平流速在上下层方向相反且在跃层处最小, 其剪切作用在波谷附近最强; 垂向流动在波前和波后分别为上升和下沉流, 两者流速值在距离波谷1/4~1/2波长位置达到最大; 在相同内孤立波振幅条件下, 上下层流体密度差越大、厚度比越小, 则波致流场越强; 随着振幅增大, 流场结构与KdV、eKdV和MCC理论模型对应波幅适用范围的描述相吻合。

分层流; 内孤立波; 粒子图像测速(Particle Image velocimetry, PIV)技术; 流场特性; 水槽实验

内孤立波作为海洋中的一类典型波动, 其传播过程中不仅会在海洋内部产生大幅度垂向运动, 而且还会诱生突发性强流[1]。海上测量和海洋遥感结果表明, 南中国海的内孤立波活动频繁, 且具有分布范围广、振幅大、持续时间长和诱导流速剪切强等特点。大量观测发现[2-4], 从吕宋海峡到东沙群岛之间海域的内孤立波常以向下凹陷波型为主, 不仅发生频率高而且波幅大, 其诱导的流速可达2 m/s以上。这类大振幅内孤立波对海洋工程结构物以及潜航器航行安全构成了严重的威胁。

开展内孤立波诱导流场结构特性研究是认识其危害性的基本出发点, 相关问题已取得许多重要的共识。例如, Hsieh等[5]基于笛卡尔网格法对重力塌陷造波生成的内孤立波流场进行了数值模拟, 指出塌陷深度相对于上下层厚度比对初始流场的影响更大; 高原雪等[6]基于MCC模型对内孤立波波致流场进行的数值分析表明, 水平速度在上下流体层中的垂向衰减很小, 而在密度跃层中的垂向衰减显著; 王伟等[7]基于KdV和mKdV模型对“平板拍击”产生的内孤立波致流场数值分析指出, 在两层流体界面和波谷之间存在“过渡水层”, 其影响范围随内孤立波振幅增大而增大。另一方面, Cai等[89]通过现场测量和理论比较, 发现内孤立波致剪切流会导致对垂直桩柱作用力和力矩的改变, 同时证实在不同密度跃层条件下小直径桩柱所受作用力不同。尤云祥等[10]在分层流水槽中测量了下凹型内孤立波对平台张力腿作用的力学特性, 指出内孤立波致流场作用力是海洋工程结构物设计过程中必须考虑的重要因素之一。刘碧涛等[11]基于薄壳有限元方法, 对内孤立波与深海立管相互作用进行了研究, 发现立管受到内孤立波致流场的水平剪切载荷可引起大幅度的运动响应, 最大纵向位移可达20倍管径以上。由此可见,获得流场的精确结构是有效分析内孤立波与结构物相互作用特性的重要前提。目前内孤立波致流场的结构研究主要还是基于经典模型的理论和数值分析, 对于在实际分层流环境中重力塌陷激发的内孤立波流场结构, 尤其是精细结构及其随分层环境变化的认识仍然十分有限。粒子图像测速(Particle Image velocimetry, PIV)技术是一种将光学成像、图像处理和计算机技术相结合的流动测量技术, 通过对流动显示图像的数值计算不仅提高了单点测量的精度和分辨率, 而且具有获取流场整体和瞬态结构的能力, 也为分层流体中内孤立波致流场精细结构测量提供了一种有效方法。为此, 本文拟采用PIV技术在不同分层环境下对由重力塌陷激发的内孤立波及其波致流场进行测量, 并将测量结果与KdV、eKdV和MCC理论模型比较, 以期获得实际分层流环境中的内孤立波致流场的精细结构, 深入探讨分层环境条件对流场结构的影响。

1 理论基础

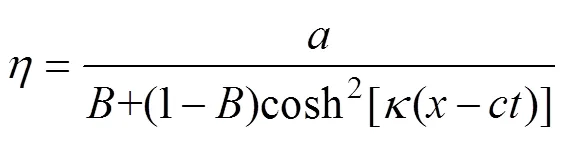
上述eKdV型方程虽然在一定程度上改善了KdV型方程对大振幅内孤立波的描述, 但仍然受限于弱非线性的条件。考虑一类完全非线性和弱色散的MCC型方程, 它可由完全非线性的欧拉方程推导, 其理论解为[13]

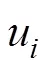
2 实验技术与方法

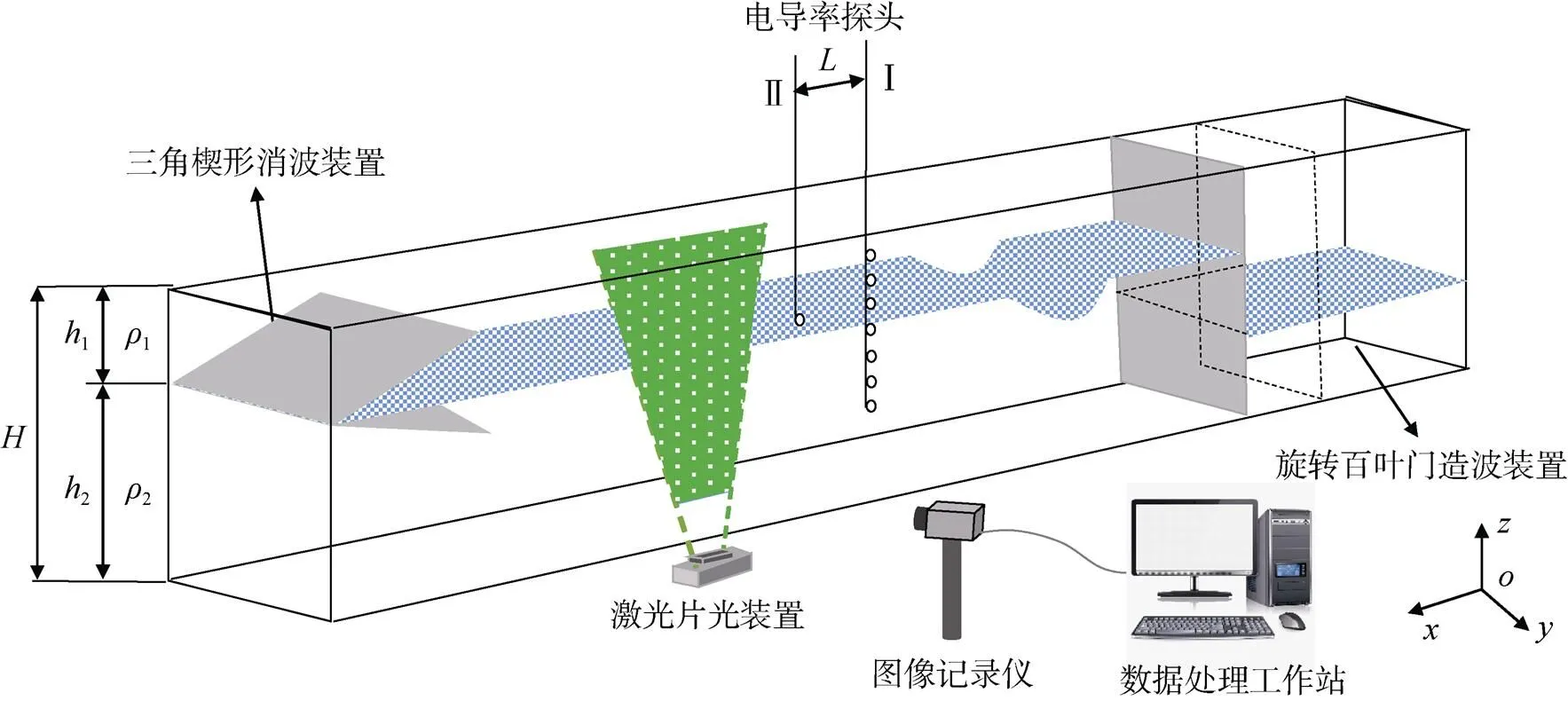
图1 实验装置示意图

图2 典型海洋跃层特征的密度和浮力频率垂向分布

激光片光装置采用双脉冲激光光源, 其功率为10 w、有效照射距离300 cm, 实验中将其置于水槽底部下方, 通过球面透镜聚焦后, 将在焦距附近形成的照射区调整至待测流场区域, 并保持示踪粒子反光性良好。图像记录仪采用Pco200 0型双快门面阵CCD, 其分辨率为204 8×204 8像素、帧率为20帧/秒, 实验中将其放在垂直于片光照射面的水槽壁面一侧, 并将实时记录的图像传入数据处理工作站。图像数据处理采用了二维快速傅里叶变换的互相关函数计算方法, 同时对初始速度矢量分布进行了修正, 可获得到速度矢量与等值线图。

示踪粒子采用聚苯乙烯颗粒, 其粒径约为10 μm, 考虑跃层附近由于密度分布不均匀造成粒子悬浮的不确定, 实验中应事先将粒子通过样本流体进行筛选, 再在制备两层流体时缓慢注入相应的配重粒子, 同时注意保持示踪粒子分布的均匀性。

3 实验结果与讨论

3.1 典型流场结构

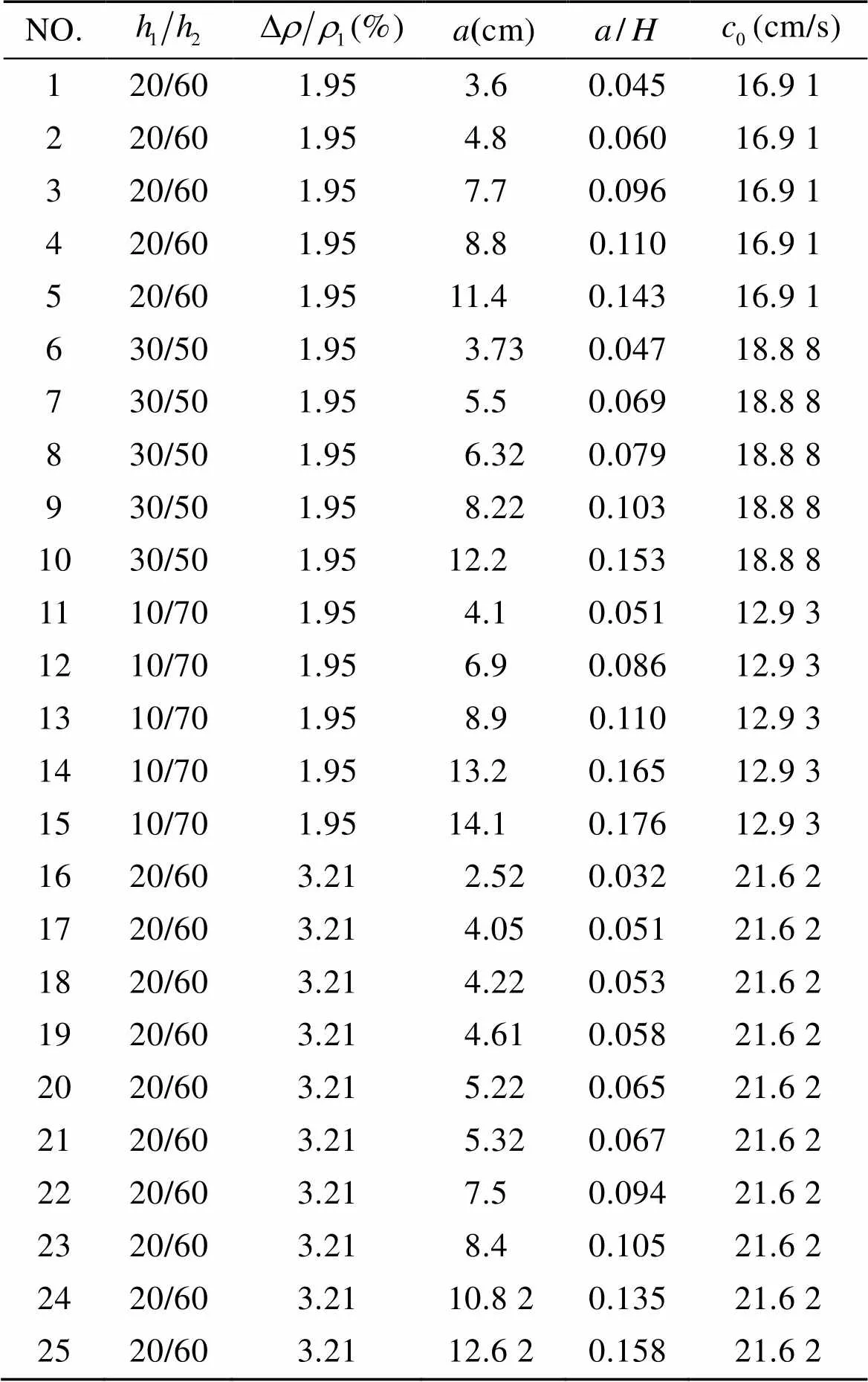
表1 试验工况

将速度矢量进行分解, 以获得水平与垂向速度场的结构与特征, 如图4所示。由图4a水平速度结构分布可知, 水平流场在密度跃层位置形成明显的剪切效应, 即跃层上方水平速度与内孤立波传播方向一致, 跃层下方水平速度与之相反且小于之, 在跃层位置处水平速度接近为零, 最大水平剪切出现在内孤立波波谷所在垂向剖面, 距离波谷区域越远, 水平剪切越小。

图3 内孤立波速度矢量和波形结构测量结果

由图4b垂向速度结构分布可知, 对下凹形内孤立波, 垂向速度呈现在波前为下沉流、波后为上升流以及在波谷处速度接近于零的特点, 且下沉流与上升流均在距离波谷1/4~1/2倍波长附近达到最大值。由于内孤立波诱导的垂向速度明显小于水平向速度, 同时波动的水平跨度相对较大, 故垂向剪切效应要比水平剪切弱得多。

图4 视场激光中心处断面水平速度u和垂向速度v的时间序列值

3.2 流场结构随振幅变化

在分层环境保持不变的条件下, 改变入射波振幅大小, 利用PIV测量内孤立波致流场结构的变化, 由此分析波致流场的特性。

图6为相同分层条件下内孤立波波谷处垂向速度时间序列图, 由图可知, 随着振幅增大, 垂向速度逐渐增大; 在波前垂向流速向下存在极小值, 在波后垂向流速向上存在最大值, 后者较前者绝对值平均大10%以上。

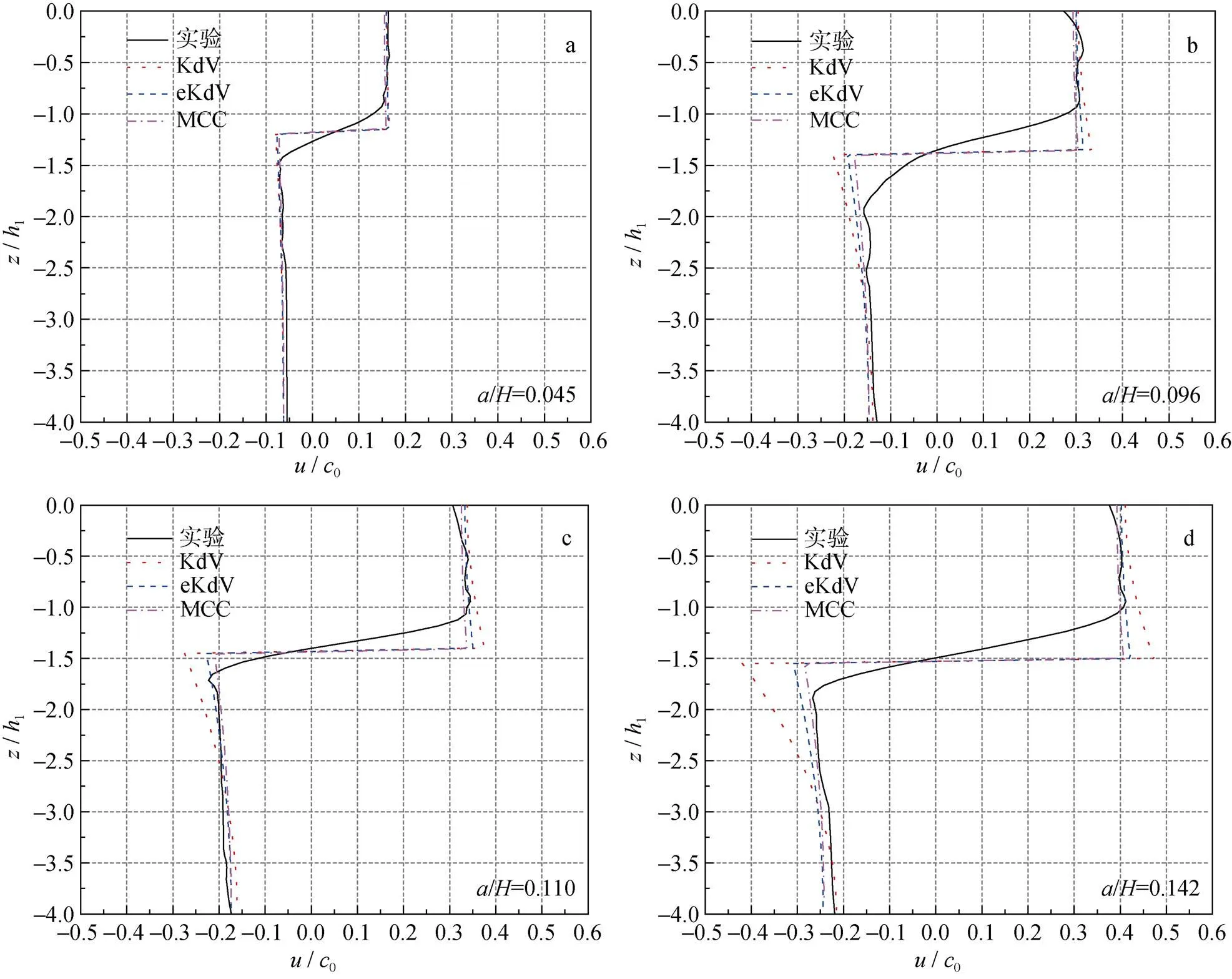
图5 内孤立波波谷断面处诱导水平速度的垂向分布

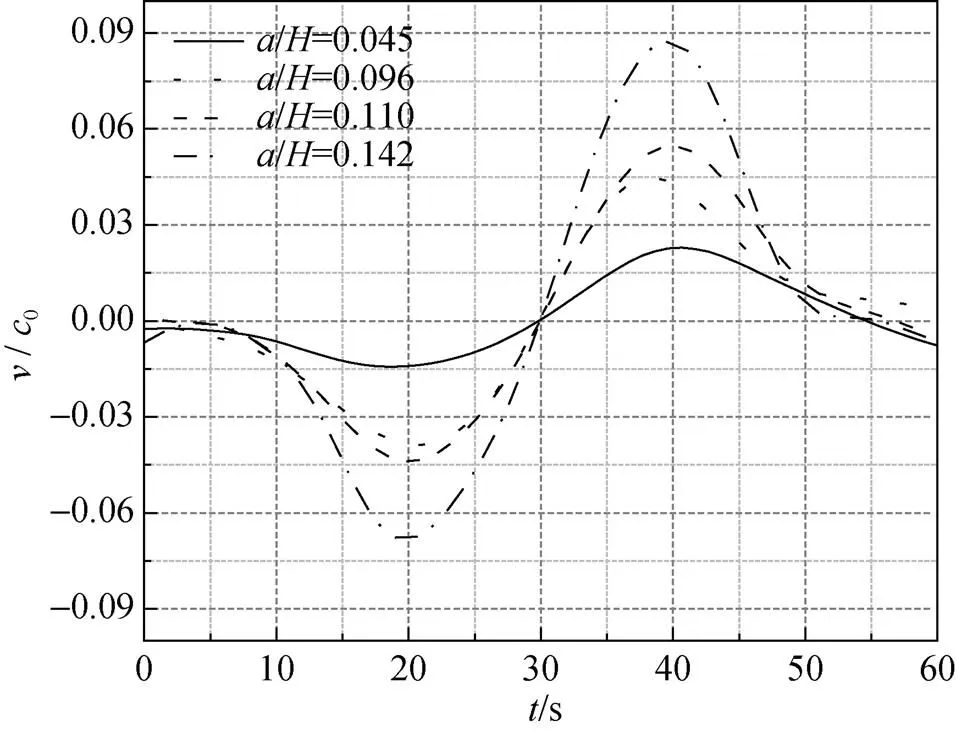
图6 内孤立波波谷处垂向速度时间序列

图7 水平与垂向最大速度比值随振幅变化

3.3 流场结构随分层环境变化

由于受到海水温度、盐度和压力等因素影响, 海洋密度层结情况不同, 导致对内孤立波致流场结构的影响存在差异, 这里考虑流体上下层密度差和厚度比对流场分布的影响。

3.3.1 上下层密度差对流场影响

3.3.2 上下层厚度比对流场影响

图8 不同密度差条件下随变化

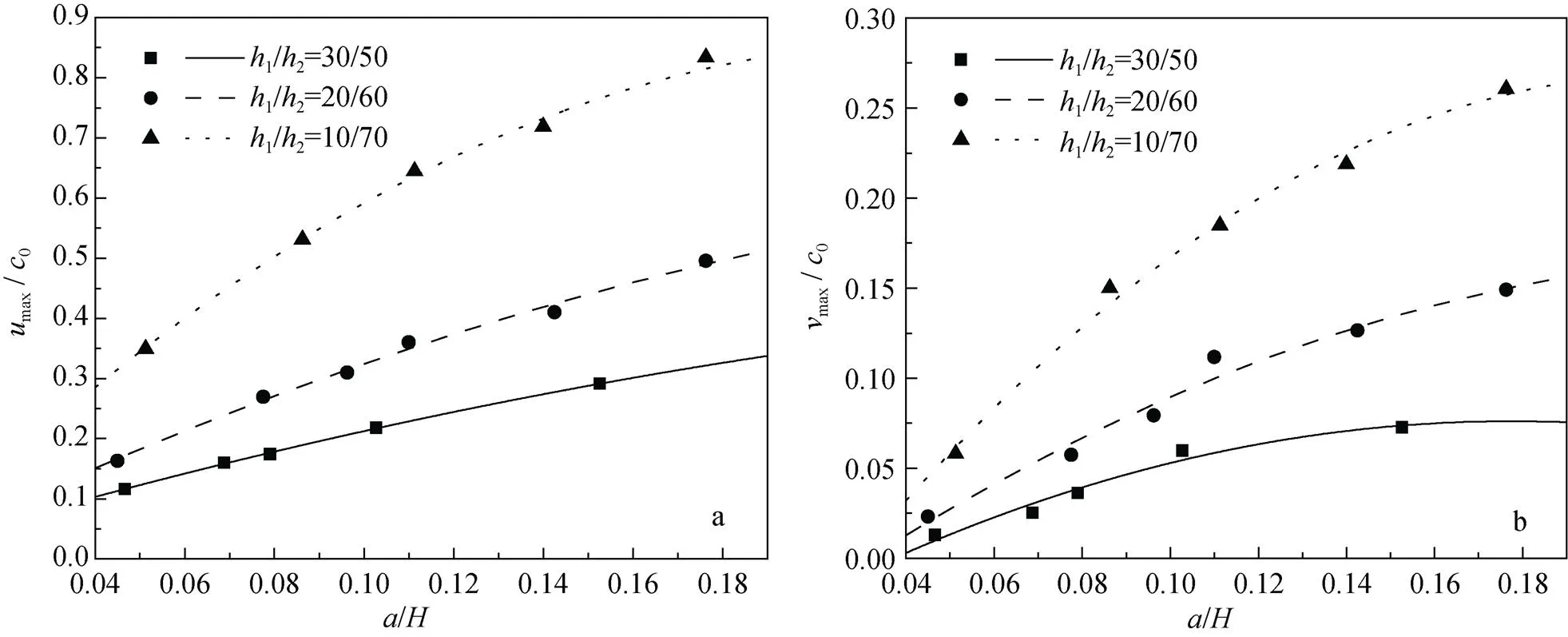
图9 不同厚度比()条件下和随振幅变化

4 结论

在大型分层水槽中, 采用重力塌陷法进行内孤立波造波以及PIV技术测量内部流速场, 结合KdV、eKdV与MCC等解析理论的速度场分析, 对下凹型内孤立波诱导流场结构及其影响因素进行了研究, 获得的主要结论如下:

2) 下凹型内孤立波在传播过程中可形成强烈的水平剪切流, 水平流动方向在上层流体中与波的传播方向一致, 在下层流体中与之相反, 在跃层位置速度趋近于零, 上层流速大于下层, 在波谷附近水平剪切作用最强, 验证了相关数值模拟的结果[6-7]; 垂向流动在波前为上升流在波后为下沉流, 在波谷前后方向相反, 且距离波谷区域越远, 垂向速度先增大后减小, 在距离波谷1/4至1/2倍波长位置附近取得最大值; 小振幅波的水平流场作用显著, 而大振幅波的垂向流场作用不可忽视。

3) 在相同内孤立波振幅条件下, 上下层流体密度差越大、厚度比越小, 则波致流场越强; 厚度比趋近于1时, 波致流场随振幅变化趋于平缓直至无法形成稳定内孤立波形, 与理论相吻合。

[1] 方欣华, 杜涛. 海洋内波基础和中国海内波[M]. 青岛: 中国海洋大学出版社, 2005: 71-73. Fang Xinhua, Du Tao. Fundamentals of oceanic internal waves and internal waves in the China seas[M]. Qingdao: China Ocean University Press, 2005: 71-73.

[2] 郭大全, 申辉. 南海北部内孤立波生成对黑潮响应的初步研究[J]. 海洋科学, 2016, 40(2): 136-144. Guo Daquan, Shen Hui. Effect of the Kuroshio on the generation of internal waves in the Northern South China Sea[J]. Marine Sciences, 2016, 40(2): 136-144.

[3] Cai S, Gan Z, Long X. Some characteristics and evolution of the internal soliton in the northern South China Sea[J]. Science Bulletin, 2002, 47(1): 21-27.

[4] 吕海滨, 申辉, 何宜军. 2009年夏季东沙群岛附近内孤立波的现场观测[J]. 海洋科学, 2013, 37(11): 54- 58.Lü Haibin, Shen Hui, He Yijun. Internal solitary wavesat the Dongsha Islands observed in the summer of 2009[J]. Marine Sciences, 2013, 37(11): 54-58.

[5] Hsieh C M, Hwang R R, Hsu R C, et al. Flow evolution of an internal solitary wave generated by gravity collapse[J]. Applied Ocean Research, 2014, 48: 277-291.

[6] 高原雪, 尤云祥, 王旭, 等. 基于MCC理论的内孤立波数值模拟[J]. 海洋工程, 2012, 30(4): 29-36. Gao Yuanxue, You Yunxiang, Wang Xu, et al. Numerical simulation for the internal solitary wave based on mcc theory[J]. The Ocean Engineering, 2012, 30(4): 29-36.

[7] 王伟, 郭海燕, 王飞, 等. 内孤立波波致流场数值模拟研究[J]. 海洋与湖沼, 2016, 47(3): 502-508. Wang Wei, Guo Haiyan, Wang Fei, et al. A numerical simulation on flow induced by internal solitary waves[J]. Oceanologia Et Limnologia Sinica, 2016, 47(3): 502-508.

[8] Cai S, Long X, Wang S. Forces and torques exerted by internal solitons in shear flows on cylindrical piles[J]. Applied Ocean Research, 2008, 30(1): 72-77.

[9] Cai Shuqun, Xu Jiexin, Chen Zhiwu, et al. The effect of a seasonal stratification variation on the load exerted by internal solitary waves on a cylindrical pile[J]. Acta Oceanologica Sinica, 2014, 33(7): 21-26.

[10] 尤云祥, 胡天群, 徐昊, 等. 分层流体中内波与半潜平台相互作用的模型试验[J]. 力学学报, 2010, 42(3): 400-406. You Yunxiang, Hu Tianqun, Xu Hao, et al. Experiments on interaction of internal waves with semi-submersible platform in a stratified fluid[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 400- 406.

[11] 刘碧涛, 李巍, 尤云祥, 等. 内孤立波与深海立管相互作用数值模拟[J]. 海洋工程, 2011, 29(4): 1-7. Liu Bitao, Li Wei, You Yunxiang, et al. Numerical simulation of interaction of internal solitary waves with deep-sea risers[J]. The Ocean Engineering, 2011, 29(4): 1-7.

[12] Helfrich K R, Melville W K. Long nonlinear internal waves[J]. Annual Review of Fluid Mechanics, 2006, 38(38): 395-425.

[13] Choi W, Camassa R. Weakly nonlinear internal waves in a two-fluid system[J]. Journal of Fluid Mechanics, 1996, 396(313): 1-36.

[14] Camassa R, Choi W, Michallet H, et al. On the realm of validity of strongly nonlinear asymptotic approximations for internal waves[J]. Journal of Fluid Mechanics, 2006, 549: 1-23.

[15] 魏岗, 苏晓冰, 杨建国, 等. 旋转百叶门重力式内孤立波造波装置[P]. 中国(发明)专利: ZL 2010101- 03635.6, 2012-01-11. Wei Gang, Su Xiaobing, Yang Jianguo, et al. Rotating louver gate gravity type internal wave making device[P]. China Patent: ZL 2010101-03635.6, 2012- 01-11.

[16] Wei G, Du H, Xu X H, et al. Experimental investigation of the generation of large-amplitude internal solitary wave and its interaction with a submerged slender body[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(2): 301-310.

[17] Walker S A, Martin A J, Easson W J, et al. Comparison of Laboratory and Theoretical Internal Solitary Wave Kinematics[J]. Journal of Waterway Port Coastal & Ocean Engineering, 2003, 129(5): 210-218.

[18] 黄文昊, 尤云祥, 王旭, 等. 有限深两层流体中内孤立波造波实验及其理论模型[J]. 物理学报, 2013, 62(8): 346-359. Huang Wenhao, You Yunxiang, Wang Xu, et al.Wave- making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth[J]. Acta Phys Sin, 2013, 62(8): 346-359.

(本文编辑: 李晓燕)

Experimental study on the flow field induced by internal solitary waves and its influence factors

WU Jun-lin, WEI Gang, DU Hui, XU Jun-nan

(College of Meteorology and Oceanography, National University of Defense Technology, Nanjing 211101, China)

To study the influence of the flow field induced by internal solitary waves (ISWs) on marine engineering structures and underwater vehicles, in a large-scale gravity-stratified fluid tank, the velocities of a series of ISWs created by gravity collapse were measured using particle image velocimetry (PIV) and its wave-induced flow field and influence factors were quantitatively analyzed. Experimental results show that the PIV technique can realize the fine measurement for the flow field induced by the large-scale solitary wave in the density-stratified fluid. The direction of the horizontal velocity below the wave profile is opposite to the one in the upper-layer fluid and the minimum velocity appears at the pycnocline, whereas the horizontal shear is the strongest near the pycnocline. The vertical flows at the front and rear of the ISWs are the descending and ascending flows, respectively, and achieve their maximums at a position that is 1/4–1/2 times the wavelength away from the trough. The velocity values at the same amplitude increase with increasing differences of density and thickness between the upper and lower layers. Moreover, as the amplitude increases, the flow field structures successively coincide with the description of the KdV, eKdV, and MCC theoretical models in their applicable ranges.

stratified fluid; internal solitary wave; PIV; flow field; experiments in water tank

Apr. 7, 2017

武军林(1993-), 男, 江苏盐城人, 硕士研究生, 研究方向为分层流体动力学, E-mail: wujunlin5252@sina.com; 魏岗,

, 教授, 博导, 主要从事海洋环境、分层流体动力学等方面的研究, 电话: 025-80830660, E-mail: weigangweigang12@163.com

P731.24

1000-3096(2017)09-0114-09

10.11759/hykx20170404001

2017-04-07;

2017-06-26

国家自然科学基金项目

[National Natural Science Foundation of China, No.11472307; Defense Technology Foundation Project, No. QX2015043104A12002]