例谈“尚简”的解题艺术

朱晓琳

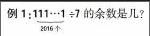
摘 要：数学解题追求“简约而不简单”的境界，“尚简”是数学解题的至真追求。为此，教师要引导学生对数学问题展开去伪存真的分析，可以从“退”中求简、“化”中求简、“换”中求简、“设”中求简 、“借”中求简、“分”中求简。通过化繁为简、删繁就简，发掘“简”的解题之道，生成“简”的解题智慧与艺术。

关键词：尚简；解题艺术；简中求道

当下的数学解题必须走出复杂化、烦琐化的倾向。简单、明快、直接、自然应当是数学学科的本质特征。教学中，教师对数学问题的表述要深入浅出，引导学生抓住问题的数学本质，去粗取精、去伪存真，优化解题思路。解题时，要化繁为简、删繁就简，从“简”中挖掘解题之道，让数学解题达到“简约而不简单”的境界。

一、 从“退”中求简

老子说，“少则得，多则惑”。在数学解题教学中，教师要引导学生“以小见大”，将复杂、烦琐甚至无从下手的数学问题化简。从简单的情形开始，或许我们就能读懂题意，理清数量关系，发现题目中蕴含的数学规律，进而找到问题解决的路径。

分析：本题看上去比较繁复，直接计算是很难得出结果的。我们可以采用“简约化”的解题原则——“以小见大”，从中可能发现规律。这也就是著名数学家华罗庚先生所倡导的“欲进先退”的解题策略。华罗庚曾经说过：“善于退、足够的退，退到最原始而不失重要性的地方是学好数学的一个诀窍。”由于1÷7=0……1；11÷7=1……4；111÷7=15……6；1111÷7=158……5；11111÷7=1587……2；111111÷7=15873。显然，每6个1除以7能够没有余数，而商也呈现出015873的反复出现现象，余数呈现出1，4， 6，5，2的周期现象。由于本题中有2016个1，因此我们用2016除以6，得336，正好是6的倍数。所以，本题中的商为15873015873…015873，余数为0。

二、 从“化”中求简

对数学问题的认知不能停留于表面，而必须深入到数学本质的层面，通过相似联想、类比推理将陌生的问题“化”成熟悉的问题。从“化”中求简，往往能够打破解题的僵局，化难为易。某种意义上，数学的“化”简来自于学生的数学直觉、数学灵感，即学生能够在瞬间产生类似于连接电路的思维通路。

例2：小红星期天在家里做作业。刚开始做作业时，小红看了一下钟面，这时分针略超过时针。做完作业，小红又看了一下钟面，发现时针和分针恰好互换了位置。你知道小红做作业用了多长时间嗎？

分析：粗略地看上去，本题中的已知条件比较特殊，没有一个数据，好像很难找到解题的路径。但是仔细读题并展开数学思考，我们就能发现题目中的一个关键条件，那就是“时针和分针恰好互换了位置”，这说明什么呢？“时针和分针恰好互换了位置”说明时针走到了原来分针的位置，分针走到了原来时针的位置。因此，时针和分针一共走了1圈。为此，我们可以将本题简易地“化”成一个“和倍问题”：分针的速度是时针的12倍，分针和时针一共走了60小格，分针走了多少格？由于“和倍问题”是我们熟悉的问题，因此本题也能迎刃而解。

三、 从“换”中求简

在数学解题中，有时我们会发现数学题目的形式非常复杂但又隐藏着一定的规律，常常让我们产生一种欲罢不能的解题欲望，但直接展开求解会比较困难、复杂。为此，我们可以对题目中一些有规律的整体元素进行换元，则有可能将题目的表征形式变得简单。整体换元能够让我们发现题目中隐含的解题规律，通过“换”的方式来寻求解题简便、巧妙的通道，进而在“曲径通幽处”诞生出迂回的“巧妙解法”。

四、从“设”中求简

有些数学问题内含的数量关系比较抽象，在解题时不容易找寻到突破口。为此，教师可以化抽象为具体，通过“假设”使抽象的数量关系显现出来。通过“假设”，可以让数学解题过程不蔓不枝、清清楚楚、干干净净。在“设”中求简，彰显的是教师“以设求解”的解题艺术。

五、 从“借”中求简

“借”是一种重要的解题策略，在数学学习中，有许多问题通过巧妙的“借与还”能够使其变得简单起来。“借”是一种智慧，通过“借来还去”，许多有难度的问题就会迎刃而解，获得非常漂亮、非常简洁的解答。

六、 从“分”中求简

数学解题总的指导原则就是“化复杂为简单”。教学中，教师可以采用“分”的策略，对复杂的数学问题进行简约化处理。当然有时运用“分”的策略解题并不是一蹴而就的，而是需要反复尝试、探索，才能获得问题的成功解决。在“分”的过程中，教师要把握数学问题的精髓，当某种“分”的方法出现障碍或问题时，要及时变换，而不能在某一种“分”法上过分纠缠。

例6：公交车A车站有公交车192辆，B车站有公交车48辆，每天从A车站发往B车站的公交车有24辆，从B车站发往A车站的公交车有21辆。那么，几天以后，B车站的公交车是A站的7倍？

分析：从题目中的关键句“每天从A车站发往B车站的公交车有24辆，从B车站发往A车站的公交车有21辆”可以看出，每天A车站都会少3辆公交车。由于题目中的问题是“几天以后，B车站的公交车是A车站的7倍”，就需要知道当B车站公交车数量是A车站的7倍时，A、B两站各有多少公交车。于是，我们可以对原来稍复杂的数学问题进行分解，让数学问题的表征变得简单些。

由题目可知A车站和B车站共有公交车192+48辆，当B车站的公交车数量是A车站的7倍时， A车站有多少辆车？显然，将A车站的公交车数量看作1份，那么B车站的公交车数量就是7份，则A车站的公交车数量为：（192+48）÷（7+1）=30（辆）。由于A车站原有公交车48辆，当B车站的公交车数量是A车站的7倍时， A车站的公交车数量为30辆，即A车站一共少了18辆公交车，又因为A车站每天少3辆公交车，故这道题的本质就是“求18辆里有几个3辆”，列式为18÷3=6。如此，通过“分解”策略，对数学问题展开剥蒜头式的分析，就能将看似繁杂的问题有效化简。

大道至简，真水无香。诚如英国著名戏剧家莎士比亚所说，“简洁是智慧的灵魂”。在数学解题教学中，教师应当删繁就简，从简中求道。教师从“退”中求简、从“化”中求简、从“换”中求简、从“设”中求简、从“借”中求简、从“分”中求简，就能以简驭繁，生成简约的解题策略。“尚简”的解题思想背后彰显的是学生数学学习的大气、睿智与深刻。教学中，教师引领着学生展开丰富、灵动、有效的数学解题实践，就能从根本上提升学生的解题素养。