基于多引导滤波器的单幅图像超分辨率技术

刘 哲，韩九强，黄世奇



基于多引导滤波器的单幅图像超分辨率技术

刘 哲1,2，韩九强2，黄世奇1

（1. 西京学院电子信息工程系，陕西 西安 710123；2. 西安交通大学电信学院计算机科学与技术系，陕西 西安 710049）

提出了一种基于多引导滤波器的单幅图像超分辨率方法。首先，该方法通过大量的自然图像建立高低分辨率图像块样本训练库，并通过聚类算法将具有相似性质的高低分辨率样本块进行聚类；其次，将输入低分辨率图像进行重叠分块，并在样本库中搜索最近邻的高低分辨率样本聚类；再次，将输入低分辨率图像块作为输入图像，与样本库中最近邻的低分辨率聚类样本作为引导图像，运用本文提出的多引导滤波器计算引导滤波器的参数；最后，利用样本库中最近邻的高分辨率聚类样本和引导滤波器的参数，通过多引导滤波器就可以重构高分辨率图像。实验结果表明，本文算法不仅能很好地重构图像的高频细节，还能很好地恢复图像的纹理特征。

超分辨率；引导滤波器；样本训练库；高频细节

0 引言

单幅图像超分辨率[1-2]（SISR）技术，是指用图像处理算法将单幅低分辨率图像转换成高分辨率图像，构建更高分辨率图像所缺失的高频细节，这在数学上是一个病态问题。高分辨率意味着图像中的像素密度高，能够提供更为丰富的图像细节，而这些细节在许多实际应用中不可或缺，所以图像超分辨率技术在医学诊断、模式识别、视频监控、生物鉴别、高清晰电视成像、遥感图像解译、高空对地观测等领域有着广泛的应用。一直以来，单幅图像超分辨率技术是视频图像处理领域研究的热门方向和一个具有相当挑战性的理论分支[1]。

传统的图像超分辨率技术有基于插值的超分辨率重建、基于重建的图像超分辨方法和基于学习的超分辨率算法[2]。SISR更先进的方法是基于统计图像先验[1,3]或基于复杂的机器学习算法[4-5]来学习从低分辨率到高分辨率的映射函数，其中最好的算法之一是基于稀疏字典学习方法，其假设可以使用字典原子的稀疏编码来表示自然图像块。特别是耦合字典学习方法[6-8]实现了很好的单幅图像超分辨率的结果。Timofte[9]通过研究指出了该方法的计算瓶颈，并提出用许多较小的字典替换单个字典，从而避免在推理期间耗时的稀疏编码步骤，大大提高了计算速度，同时保持与以前方法相同的超分辨率结果精度。

稀疏字典学习技术[10-12]，其主要思想是高低分辨率图像块对具有相同的稀疏字典表示。然而，该稀疏约束同时涉及在训练和推理阶段最小化L1范数函数，从而导致复杂的数学计算[13-15]。最近，随着学者对自然图像块流形结构的更深的理解，基于流形学习方法的单幅图像超分辨率技术[10-13,16]有了很大进展。流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律。近年来，我们目睹了从耗时复杂的稀疏字典技术向更高效的流形学习模型的转变。基于流形的学习，将耗时的推理阶段学习转为离线学习，大大降低了学习的复杂性，提高了算法的效率和精度。

在本文中，提出了一种基于多引导滤波器的流形学习单幅图像超分辨率方法，该方法能实现快速在线学习。首先，该方法通过大量的自然图像建立高低分辨率图像块样本训练库，并通过聚类算法将具有相似性质的高低分辨率样本块进行聚类；其次，将输入低分辨率图像进行重叠分块，并在样本库中搜索最近邻的高低分辨率样本聚类；再次，将输入低分辨率图像块作为输入图像，与样本库中最近邻的低分辨率聚类样本作为引导图像，运用本文提出的多引导滤波器计算引导滤波器的参数；最后，利用样本库中最近邻的高分辨率聚类样本和引导滤波器的参数，通过多引导滤波器就可以重构高分辨率图像。实验结果表明，本文算法不仅能很好地重构图像的高频细节，还能很地的恢复图像的纹理特征，同时本文算法具有很高的执行效率。

1 多引导滤波器原理及其性质

1.1 引导滤波器

引导图像滤波器由He等人[11]提出，其滤波输出是引导图像的线性变换。在引导滤波的定义中，用到了局部线性模型。该模型认为，某函数上一点与其邻近部分的点成线性关系，一个复杂的函数就可以用很多局部的线性函数来表示，当需要求该函数上某一点的值时，只需计算所有包含该点的线性函数的值并做平均即可。一方面，引导图像滤波器和双边滤波器一样具有很好的保留边缘、平滑噪声的作用；另一方面，在引导图像的作用下，该滤波器可以使输出图像比输入图像具有更多边缘信息。

引导滤波器的关键就是假设引导图像和滤波输出图像之间是局部线性模型。在以像素点为中心的窗口w中，输出图像是引导图像的线性变换：

q＝aI＋b"Îw(1)

式中：(a,b)为常量。该线性模型假定当且仅当引导图像有边缘时才会有边缘，这是因为Ñ＝Ñ。为了求出线性系数(a,b)要对滤波输入图像进行约束。假设输出图像是由输入图像减去噪声得到的：

q＝p－n(2)

为了求出线性系数(a,b)的最优解，要使和之间的差异最小，等价为最小化窗口w中的代价函数：

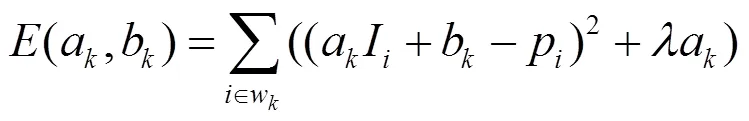
公式(3)是一个线性回归模型，它的最优解是：

1.2 多引导滤波器

q＝1k1i＋2k2i＋…＋aI＋b"Îw(6)

式中：(1k,2k, …,a,b)是常量，为了求出线性系数(1k,2k, …,a,b)，要对滤波输入图像进行约束。假设输出图像是由输入图像减去噪声得到的：

q＝p－n(7)

为了求出线性系数(1k,2k,…,a,b)的最优解，要使和之间的差异最小，等价为最小化窗口w中的代价函数：

式中：1,2, …,为正则化参数。公式是一个线性回归模型，运用最小二乘可以对(8)式进行求解。先对(8)式中的各参数求导，使得导数等于0：

…………

对上面的各等式进行移项得到：

…………

对上面各等式(9)、(10)、(11)、(12)统一写成矩阵的形式，见式(13)：

＝(13)

式中：

＝(¢)－1¢(14)

因此，通过式(6)和(14)可以计算得到输出图像。

1.3 多引导滤波器的性质

基于学习的超分辨率方法，首先需要构建高低分辨率图像的训练样本库，样本训练库在构建时，需要对高低分辨率图像的训练库的样本进行聚类，最直接的聚类是根据样本特征图像灰度相似度进行聚类。然后通过学习训练样本，对高低分辨率样本图像之间的关系进行编码（encoding），最后对于低分辨率测试图像，在样本库中搜索最接近的聚类，利用上述学习到的编码关系指导超分辨率重建过程。

设图像1、2、…、I是样本库中同一聚类，即它们具有灰度上和结构上的相似性，即存在以下的关系：

1≈2≈…≈I(15)

下面我们就这种情况讨论多引导滤波器的性质。

1.3.1 边缘保持功能

要讨论多引导滤波器的性质，设输入图像和引导图像近似相等，即1≈2≈…≈I≈，代入(6)式得到：

q≈(1k＋2k＋…＋a)1i＋b(16)

令a＝1k＋2k＋…＋a及1i＝1i，则(16)式变为：

q≈aI＋b(17)

可以看出，在此种情况下，多引导滤波器的表达式和单引导滤波器表达式相似，于是可以求出：

下面进行讨论：

1）Ñq＝aÑI，即当输入图像有梯度时，输出图像也有类似的梯度，这就是可以解释均值滤波器具有梯度保持功能；

2）当图像处于边缘时，方差2的取值比较大，当≪2时，a®1，b®0，q＝I，此时多引导滤波器具有边缘保持功能；

3）当图像处于平坦区域时，方差2的取值比较小，当≫2时，a®0，b®1，q＝，此时多引导滤波器具有图像平滑功能。

另外，我们考虑更为一般的情况，对于(6)式表示的多引导滤波器，求解(8)式代价函数，并且满足1≈2≈…≈I≈和1≈2≈…≈≈，于是可以得到参数(a,2k,…,a,b)的通用解：

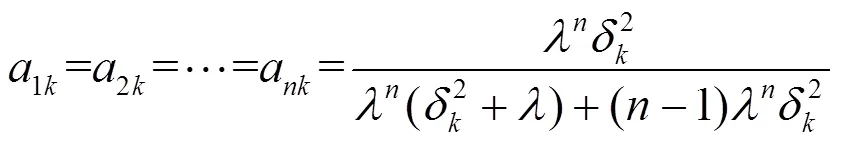
b＝－(1k＋2k＋…＋a)(20)

且满足：

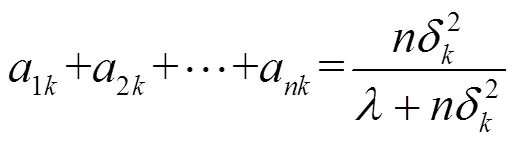
下面进行讨论更为一般的情况：

1.3.2 结构保持功能

有趣的是，多引导滤波器不是简单的边缘保持平滑滤波器。由于q＝aI＋b的局部线性模型，使得可以将结构从引导图像转移到输出图像上，即使滤波输入是平滑的也同样满足这个性质。从这点上讲，引导滤波器和流形学习具有类似的性质。

假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律。也就是说，在局部区域内，高维流形和低维流形具有类似的结构。

2 基于多引导滤波器超分辨率技术

2.1 样本训练库构建

基于多引导滤波器超分辨率技术，首先构建训练样本库。我们通过搜集大量自然图像，建立了丰富的低分辨率（LR）样本库及其对应的高分辨率（HR）样本库。

高分辨率（HR）图像块h和低分辨率（LR）图像块l存在以下关系：

l＝(hÄ)¯(22)

式中：Ä代表卷积；是高斯卷积核；¯代表下采样；表示下采样尺度因子。

2.2 算法实现

基于多引导滤波器超分辨算法实现过程如下：

1）对构建的样本库按照灰度相似性进行聚类，本文采用两个图像块对应点像素值之差的绝对值之和（SAD）作为相似度的标识，用来度量两个图像块的相似度。设有两个图像块和，如果两个图像块对应点像素值之差的绝对值之和（SAD）满足式(23)的关系，则图像块和是一个聚类，式中是选择的阈值：

通过式(23)可以将低分辨率样本库和对应高分辨率样本库进行聚类。

2）设样本训练库中低分辨率样本块l的大小为5×5，高分辨率样本快h的大小为5×5，表示尺度因子。

3）将输入的低分辨率图像LR划分成5×5的子块，相邻子块的重叠区域宽度为2个像素，构成匹配图像块。图像块在样本训练库中进行搜索，找到与之匹配的聚类，这个聚类有个相似低分辨块(l1,l2,…,lk)，与之对应的是个相似高分辨块(h1,h2,…,hk)。

4）运用双三次插值将(l1,l2,…,lk)和插值放大到5×5。对放大后的引导图像(l1,l2,…,lk)和输入图像，利用公式(6)和(14)，可以计算出多引导滤波器的输出图像，由此可以计算出参数(1,2,…,a,b)。

＝1h1＋2h2＋…＋ahk＋b(24)

6）合并所有的超分辨率重构的匹配窗，相邻图像块重叠区域的像素值使用平均融合得到，这样就求出了最终的超分辨率图像HR。

3 实验和分析

在本文实验中，选择测试的环境为：

1）操作系统Windows XP SP3；

2）应用程序开发环境Matlab 2012a；

3）计算机配置Inter Core i5，主频3.5GHz，8.0GB内存。

3.1 多引导滤波器的特性实验

为了对多引导滤波器的特性进行验证，我们选择了图1中的(a)作为输入图像，图1中的(b)、(c)、(d)3幅图像作为引导图像，而且这3幅引导图像逐渐变得有些模糊，这主要是为了验证在引导图像逐步变得模糊情况下，多引导滤波器能否保持图像的边缘。由于本文基本图像块的大小选择为5×5，所以多引导滤波器的半径为＝3，图1中(e)、(f)、(g)、(h)分别是在正则化参数取不同值时多引导滤波器的图像，由输出图像结果可以得到以下几个结论：

1）引导滤波器具有良好的图像边缘保持和增强功能，由图1中(e)、(f)、(g)、(h)输出图像结果可以看出，在正则化参数比较小的情况下，尤其是当正则化参数＝0.1（图1(e)）时，多引导滤波器的输出对图像边缘的保持效果尤为明显。

2）由图1中(e)、(f)、(g)、(h)输出图像结果可以看出，随着正则化参数原来越大，多引导滤波器输出图像变得越来越模糊。所以在选择用多引导滤波器时，一定要选择合适的参数。

3）在输入图像和部分引导图像质量比较好，部分引导图像质量下降情况下（如变得模糊等），总体上不太会影响多引导滤波器的输出。

4）多引导滤波器可以利用积分图和并行化计算来进行加速，所以该滤波器的执行效率很高，如果运用GPU就可以达到实时计算。

根据实验结果，我们选取正则化参数＝0.1，来对本文所提方法进行验证。

3.2 主观对比分析

将本文提的算法分别与Kim算法[17]、Wang算法[18]、Sun算法[19]进行比较分析，Kim算法基于稀疏回归和自然图像先验、Wang算法基于半耦合字典学习、Sun算法主要基于梯度分布先验。同一算法对不同图像选取相同的参数。主观效果如图2和图3所示，选择超分辨率图像的局部图像（如图中矩形框标记的部分）进行局部对比分析。对图2的处理中，Sun算法和Wang算法在图像的边缘处会产生锯齿、锐度不够；Kim算法在图像的边缘处产生了轻微振铃效应，边缘比较模糊；本文算法边缘保持得很好，没有伪影等不良现象产生，边缘锐度较好。本文算法的整体清晰度和图像边缘锐度明显好于其他3种方法，头部和石头图像部分的纹理也比较清晰，但是本文算法在图像边缘也会产生的锯齿效应。

图1 多引导滤波器实验结果

图2 四种算法超分辨率对比图

（(a)与(e)是Sun算法结果，(b)与(f)是Wang算法结果，(c)与(g)是Kim算法结果，(d)与(h)是本文算法结果）

Fig.2 Comparison of four super - resolution algorithms result（(a)and (e) Sun,(b) and (f)Wang，(c) and (g) Kim，(d) and (h) proposed）

图3 四种算法超分辨率对比图

（(a)与(e)是Sun算法结果，(b)与(f)是Wang算法结果，(c)与(g)是Kim算法结果，(d)与(h)是本文算法结果）

Fig.3 Comparison of four super - resolution algorithms result（(a）and (e) Sun, (b) and (f)Wang, (c) and (g) Kim, (d) and (h) proposed）

3.3 客观指标对比分析

对客观效果评估，用可量化的技术指标来进行评价。本文用图像峰值信噪比（PSNR）和图像结构的相似性（SSIM）评价不同算法的性能。表1是测试图像在2倍超分辨率放大情况下的客观评价结果。本文所测试的3幅测试图像来源于加州大学伯克利分校图像分割数据库。从表1的分析数据可以看出，本文提出的方法在所有情况下都比其他3种方法获得的结果要好，表现最优。

表1 PSNR和SSIM比较

为进一步评价不同算法超分辨性能，图2、图3分别比较了使用4种不同算法重建的结果。可以看出，Sun算法不能有效恢复图像的高频信息，生成的图像有些模糊。与Sun算法结果相比较，经典的Wang算法通过学习HR与LR图像间的字典表示，在一定程度上能有效恢复出LR图像中丢失的高频细节，得到的结果比较清晰。Kim算法的效果从整体上看与Wang算法效果相当。从视觉质量上看，Wang算法能够得到比Sun算法更多的高频细节，与上述3种方法得到的结果相比，本文提出的基于多引导滤波器单幅图像超分辨率算法在保持图像边缘和恢复纹理细节方面都有不同程度的改善，得到的结果不仅边缘更清晰更真实，而且纹理更加丰富。这是由于图像的局部流形结构在局部范围可以保持良好的一致性，在学习过程中，结合最近邻域自相似特性，使得参与重建的图像块均与目标图像块具有相似的结构，因而能获得较好的重建质量。

3.4 算法运行时间比较分析

为了分析比较4种不同算法的运行时间，对图像大小为64×32个像素的原始图像分别放大2倍、3倍、4倍、5倍，不同算法在不同放大倍数的情况下，其运行时间如图4所示。由图4可以看出，本文所提算法的运行时间大大低于其他3种算法，随着放大倍数的增加，其他3种算法的运行时间快速增加，而本文算法运行时间增加比较缓慢。当图像超分放大5倍时，本文算法的执行效率几乎是Sun算法执行效率的100倍。之所以本文算法效率很高，其主要原因是本文算法将最耗时的学习训练改为了离线学习，在进行本文算法超分辨计算时，只需通过查表，找到对应的映射函数，从而大大提高了算法的运行效率。

图4 图像不同放大倍数运行时间

4 结论

在本文中，提出了一种基于多引导滤波器的流形学习单幅图像超分辨率方法，该方法能实现快速在线学习。首先，该方法通过大量的自然图像建立高低分辨率图像块样本训练库，并通过聚类算法将具有相似性质的高低分辨率样本块进行聚类；其次，将输入低分辨率图像进行重叠分块，并在样本库中搜索最近邻的高低分辨率样本聚类；再次，将输入低分辨率图像块作为输入图像，与样本库中最近邻的低分辨率聚类样本作为引导图像，运用本文提出的多引导滤波器计算引导滤波器的参数；最后，利用样本库中最近邻的高分辨率聚类样本和引导滤波器的参数，通过多引导滤波器就可以重构高分辨率图像。实验结果表明，本文算法不仅能很好地重构图像的高频细节，还能很好地恢复图像的纹理特征，同时本文算法具有很高的执行效率。

[1] Freeman W T, Jones T R, Pasztor E C. Exaple-based super-resolutio[J]., 2002, 22(2): 56-65.

[2] Glasner Daniel, Bagon Shai, Irani Michal. Super resolution from a single image[C]//12, 2009: DOI:10.1109/ICCV.2009.5459271.

[3] Fattal R. Upsampling via Imposed Edges Statistics[J]., 2007, 26(3): 95.

[4] DONG C, Change Loy C, HE K, et al. Learning a deep convolutional network for image super-resolution[C]//, 2014: 35-40.

[5] YANG C Y, YANG M H. Fast direct super-resolution by simple functions. [C]//, 2015: 223-227.

[6] WANG S, ZHANG L, LIANG Y, et al. Semi-coupled dictionary learning with applications to image super-resolution and photo-sketch synthesis[C]//, 2012: 79-84.

[7] CUI Z, CHANG H, SHAN S. Shan, et al. Deep network cascade for image super-resolution [C]//, 2014: 49-64.

[8] Zeyde R, Elad M, Protter M. On single image scale-up using sparse-representations[J]., 2010: 541-552.

[9] FAN W, YEUNG D Y. Image hallucination using neighbor embedding over visual primitive manifolds[C]//, 2007: 1-7.

[10] Timofte R, Smet V D, Gool L V. Anchored neighborhood regression for fast example based super-resolution[C]//, 2013: 256-266.

[11] YANG C Y, YANG M H. Fast direct super resolution by simple functions[C]/, 2013: 105-112.

[12] YANG J, LIN Z, Cohen S. Fast image super resolution based on in-place example regression[C]//, 2013: 753-761.

[13] Timofte R, Rothe R, Gool L V. Seven ways to improve example-based single image super resolution[J].,2016: 1865-1873.

[14] YANG J, WRIGHT J, MA Y. Image super resolution via sparse representation[J]., 2010, 19(11): 2861-2873.

[15] Zeyde R, Elad M, Protter M. On single image scale up using sparse-representations[C]//, 2012: 6920: 711-730.

[16] Timofte R, Smet V D, Gool L V. A+: Adjusted anchored neighborhood regression for fast super-resolution[C]//, 2014: 283-290.

[17] Kim K I, Kwon Y. Single-image super-resolution using sparse regression and natural image prior[J]., 2010, 32(6): 1127-1133.

[18] WANG S, ZHANG L, LIANG Y, et al. Semi-coupled dictionary learning with applications to image super-resolution and photosketch synthesis[C]//, 2012: 586-593.

[19] SUN J, XU Z, et al. Image super-resolution using gradient profile prior[C]//, 2008: 862-871.

[20] Nasrollahi K, Moeslund T B. Super-resolution: a comprehensive survey[J]., 2014, 25(6): 1423-1468.

[21] Mairal J, Bach F, Ponce J, et al. Non-local sparse models for image restoration[C]//, 2010, 30(2): 2272-2279.

[22] Glasner D, Bagon S, Irani M. Super-resolution from a single image[C]//, 2009, 30(2): 349-356.

[23] Freedman G, Fattal R. Image and video upscaling from local self-examples[J]., 2011, 30(2): 1-11.

[24] Kawano H, Suetake N, Cha B, Aso T. Sharpness preserving image enlargement by using self-decomposed codebook and Mahalanobis distance[J]., 2014, 27(6): 684-693.

[25] ZHANG Y Q, LIU J Y, YANG W H, et al. Image super-resolution based on structure-modulated sparse representation[J]., 2015, 24(9): 2797-2810.

[26] ZHANG Y Q, XIAO J S, LI S H, et al. Learning block-structured incoherent dictionaries for sparse representation[J]., 2015, 58(10):1-15.

[27] YANG C Y, HUANG J B, YANG M H. Exploiting self-similarities for single frame super-resolution[C]/10th(), Queen-stown, New Zealand: Springer, 2016: 497-510.

Single Image Super-Resolution Based on Multi-Guided Filtering

LIU Zhe，HAN jiuqiang，HUANG Shiqi

(1.,,’710123,; 2.,,’710049,)

In this paper, a single image super-resolution method based on multi-guided filtering is proposed. First, anexemplar training database consisting of pairs of low-resolution and corresponding high-resolution image patches is constructed using many natural images. High- and low-resolution image patches with similar properties are clustered using a clustering algorithm. Next, the low-resolution input image is divided into overlapping patches, and the nearest neighbor high-and low-resolution sample cluster is searched againstthe exemplar training database. Then, the low-resolution input image patch is used as the new input; the nearest neighbor low-resolution clustering sample is used as the guide image. The multi-guided filter is used to calculate the parameters of the guide filter. Finally, the high-resolution images can be reconstructed with the multi-guided filter using the nearest neighbor high-resolution clustering samples and the parameters of the multi-guide in the sample bank. Experimental results show that the proposed algorithm not only reconstructs the high-frequency detail of an image, but also recovers the texture features.

super resolution，guided filtering，exemplar training database，high frequency detail

TP391.41

A

1001-8891(2017)10-0920-08

2017-01-25；

2017-03-06.

刘哲（1972-），男，教授级高工，博士，研究方向为机器视觉、人工智能及模式识别。

国家自然科学基金（61473237）。