基于排列熵的城市化区域地下水系统复杂性测度

张永嘉，刘 东,2,3,4

(1.东北农业大学水利与土木工程学院，哈尔滨 150030；2.农业部农业水资源提高利用重点实验室，哈尔滨 150030；3.黑龙江省粮食产能提升协同创新中心，哈尔滨 150030;4.黑龙江省普通高校节水农业重点实验室，哈尔滨 150030)

0 引 言

城市地下水水文系统复杂性作为一个较新的研究方向被人们广为关注，它直接影响着区域农业生产、旱涝灾害等相关的生产活动。在全球气候变化的今天，地下水水文系统复杂性日益显著，研究地下水水文系统的复杂性可为水资源系统的预测以及后期对水资源的优化配置奠定基础，通过预测对区域的水资源进行分配，更有效、合理、可持续的利用水资源。

在研究复杂性科学中熵理论最为常用，近似熵[1]、多尺度熵[2]、风险熵[3]、小波熵[4]、信息熵[5]、样本熵(Sample Entropy)[6]、最大熵原理[7]等都是熵理论算法。其中排列熵(PE)计算简便、抗噪声能力强[8]。近些年国内外研究以及取得的研究成果主要有：颜云华和吴志丹结合多元经验模态分解和PE进行高速列车故障工况检测[9]；从华等运用基于PE的连续隐马尔可夫模型诊断4种状态齿轮故障[10]；Hamed Azami等运用改进后的PE算法分析多时间尺度下脑电图中眨眼时颅内猝发反应的变化[11]；Sesham Srinu等人运用振幅感知PE来增强、合成信号，并对脑神经数据进行处理[12]。PE虽然在相应领域中都取得一定成果，但在水文水资源领域运用较少。

本文采用PE对哈尔滨逐日地下水埋深序列复杂性进行测度，在结果准确的基础上，选取更可靠、直观的熵理论方法分析区域地下水水文系统的复杂性，并探究当地下垫面条件与地下水水文系统复杂性的相关关系，揭示影响城市区域地下水水文系统的关键因素。

1 研究区域与方法

1.1 研究区域

哈尔滨是黑龙江省省会，地处东经125°42′～130°10′、北纬44°04′～46°40′是中国东北北部的政治、经济、文化中心。全市总面积约为53 840 km2，辖9个市辖区、7个县，代管2个县级市，其中市辖区面积10 198 km2。2014年户籍总人口994万人。哈尔滨的气候属中温带大陆性季风气候，冬长夏短，全年平均降水量569.1 mm，降水主要集中在6-9月，夏季占全年降水量的60%[13]。在下垫面条件(例如地形、地貌等)的影响下，该地区地下水分布不均，复杂性特征明显，因此揭示区域地下水埋深序列复杂特征，为区域地下水水资源预测和合理性分配奠定基础。

1.2 资料来源

从黑龙江省气象局收集到哈尔滨水文局下属的10个区域从2008年到2013年的逐日的地下水埋深监测资料(n=2192)。哈尔滨各区域监测地点地下水埋深均表现出周期性变化，但各个区域地下水埋深变化幅度中含有随机、非线性等复杂性特征，使得各区域地下水埋深变化各不相同，其中市区、五常、依兰、尚志和延寿有递减趋势，而其余区域都呈现递增趋势。

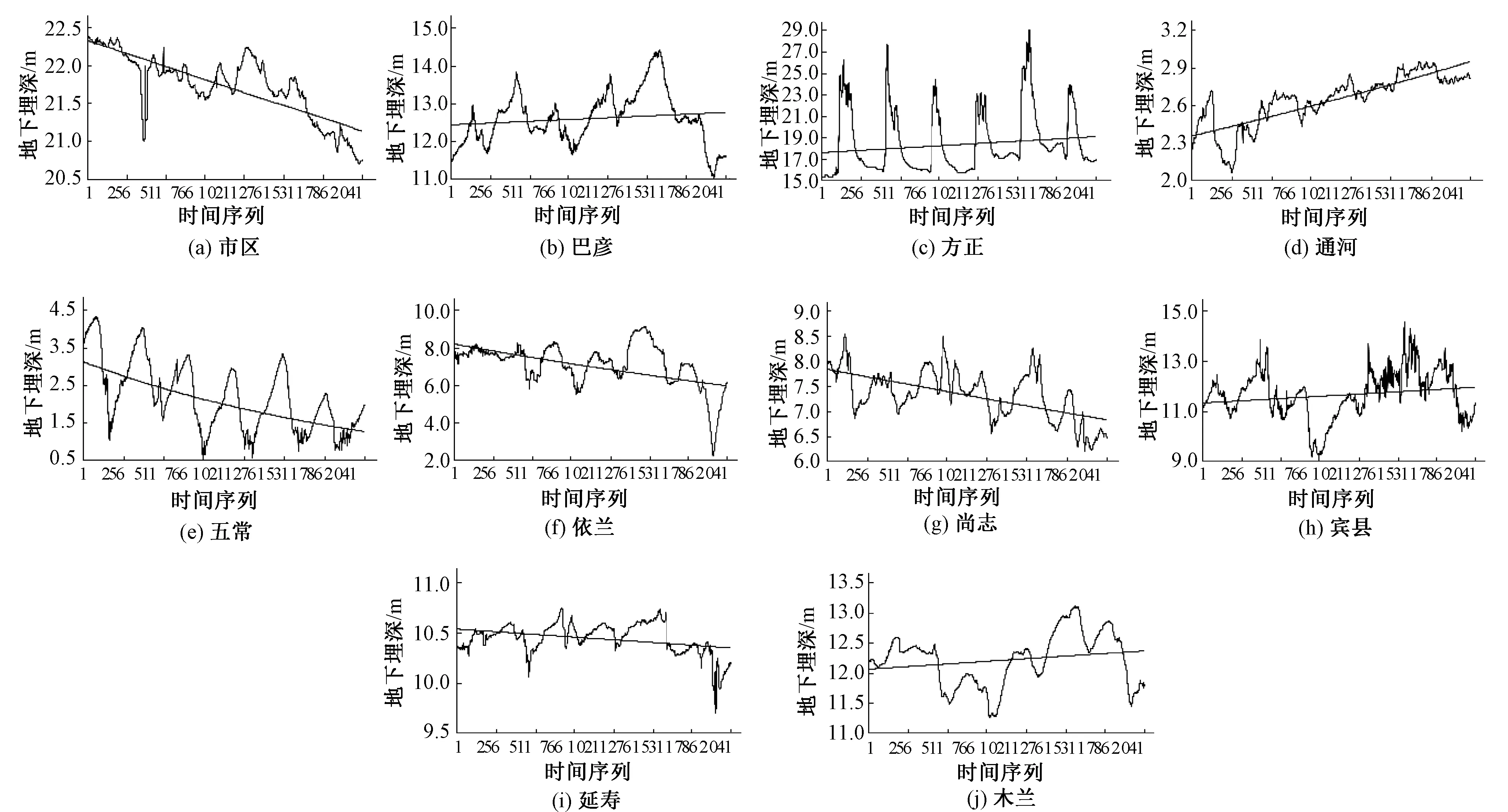
图1 哈尔滨市各区域逐日地下水埋深序列变化曲线(2008-2013)Fig.1 Variation curves of daily groundwater depth series of each county in Harbin (2008-2013)

1.3 研究方法--排列熵

Christoph Bandt[14]等人提出了一种衡量一维时间序列复杂度的算法PE (Permutation Entropy) ，具有计算简单、抗噪声干扰能力强等特点。

PE具体算法如下[18]：

(1)设时间序列Xi，i=1,2,…,n，进行相空间重构，得到矩阵Xk；

(1)

式中：m，τ分别为嵌入位数和延迟时间；K=n-(m-1)τ。

(2) 将Xi重构矩阵中的第j个重构分量[xj,xj+τ,…,xj+(m-1) τ]，按照升序重新排列，j1,j2,…,jm，即：

xi+[j(1)-1] τ≤xi+[j(2)-1] τ≤ … ≤xi+[j(m)-1] τ

(2)

(3) 时间序列Xi排列方式共m!种排列，计算每一种符号序列出现的概率为P1,P2,…,Pm，则PE为:

PEp(m)=-∑mj=1pjlnPj

(3)

PEp(m)表示了时间序列Xi的随机程度，PE值越大，时间序列复杂性越大，PE值越小，时间序列复杂性越小。

2 结果与分析

采用上述方法，其中嵌入位数m取4，延迟时间τ取2，利用Matlab R2010b软件编程，计算哈尔滨各区域逐日的地下水埋深序列PE值，结果见表1。

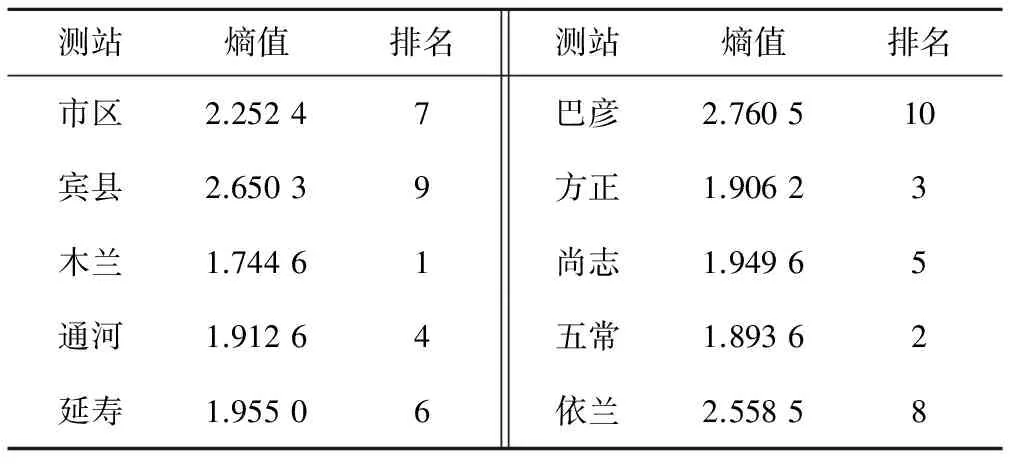
表1 基于PE的哈尔滨市各区域逐日地下水埋深序列熵值及排序Tab.1 The values of entropy of daily groundwater depth series of each county in Harbin based on PE and the orders

若测站地下水埋深序列PE值越大，则复杂性越强，地下水埋深序列的可预测性降低。由表1可知，哈尔滨各测站地下水埋深序列可预测性从高到低为：木兰>五常>方正>通河>尚志>延寿>市区>依兰>宾县>巴彦，并根据PE值将复杂性分为3级，熵值在2.900～2.400之间为Ⅰ级，在2.400～1.900之间为Ⅱ级，在1.900～1.400之间为Ⅲ级，见表2，并绘制其地下水埋深序列复杂性空间分布图，见图2。

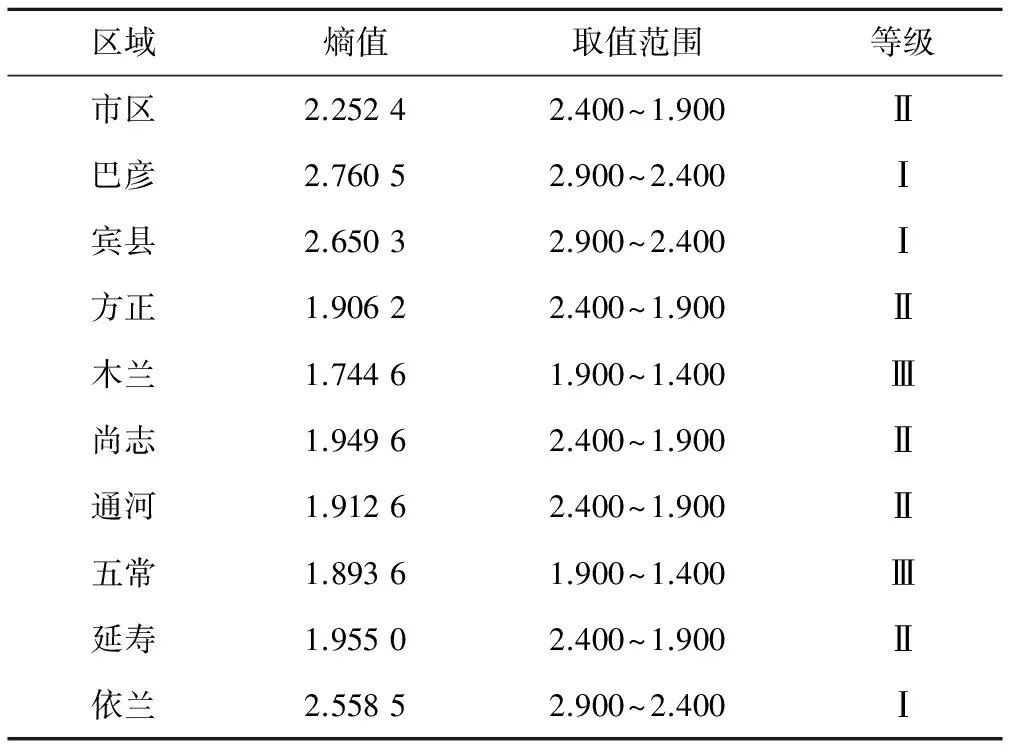
表2 各区域逐日地下水埋深序列复杂性分级Tab.2 Complexity grade of daily groundwaterdepth series in each county

由图2可知，巴彦、宾县、依兰3个区域地下水埋深序列复杂性为Ⅰ级，等级最高，说明这3个区域的地下水资源预测难度大，影响因子较多；市区、方正、尚志、通河、延寿5个区域地下水埋深序列复杂性为Ⅱ级，等级居中，说明这5个区域的地下水资源预测难度一般，影响因子数量一般；木兰、五常2个区域地下水埋深序列复杂性为Ⅲ级，等级最低，说明这两个区域的地下水资源预测容易，影响因子较少。

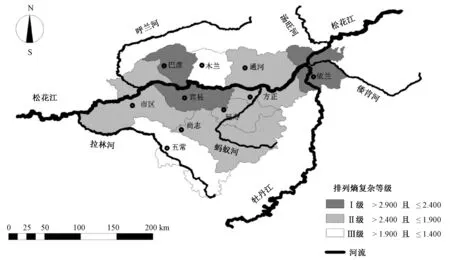
图2 哈尔滨各区域逐日地下水埋深序列复杂性空间分布Fig.2 Complexity spatial distribution of daily groundwater depth series of each county in Harbin

3 讨 论

本文选择哈尔滨地区两个下垫面条件(山地面积、水域面积)，分析两个条件与地下水埋深序列复杂性进行相关性分析，探究其对地下水水文系统复杂性的影响。分别计算山地面积比例与水域面积比例，并将其划分为3级，见表3。其中山地面积比例在60%～80%为Ⅰ级，在35%～60%为Ⅱ级，在0%～35%为Ⅲ级)，而水域面积在4.9%～7.0%为Ⅰ级，在2.5%～4.9%为Ⅱ级，在1.0%～2.5%为Ⅲ级。在哈尔滨各区域逐日地下水埋深序列复杂性空间分布底图上分别绘制山地面积比例和水域面积比例空间分布图，见图3和图4。

由图3可知，巴彦、依兰、尚志、延寿和方正的地下水埋深序列复杂性等级与山地面积比例等级一致，说明这5个区域的山地地形对地下水水文系统影响较大；宾县和五常地下水埋深序列复杂性等级与山地面积比例等级相差2级，说明这2个区域的山地地形对地下水水文系统影响较小；其余区域两者等级则相差1级，说明这3个区域的山地地形对地下水水文系统影响能力一般。

由图4可知，巴彦和依兰的地下水埋深序列复杂性等级与水域面积比例等级一致，说明这两个区域的水域对地下水水文系统影响较大；宾县和五常的地下水埋深序列复杂性等级与水域面积比例等级相差2级，说明这两个区域的水域对地下水水文系统影响较小；其余区域两者等级则相差1级，说明这6个区域的水域对地下水水文系统影响能力一般。

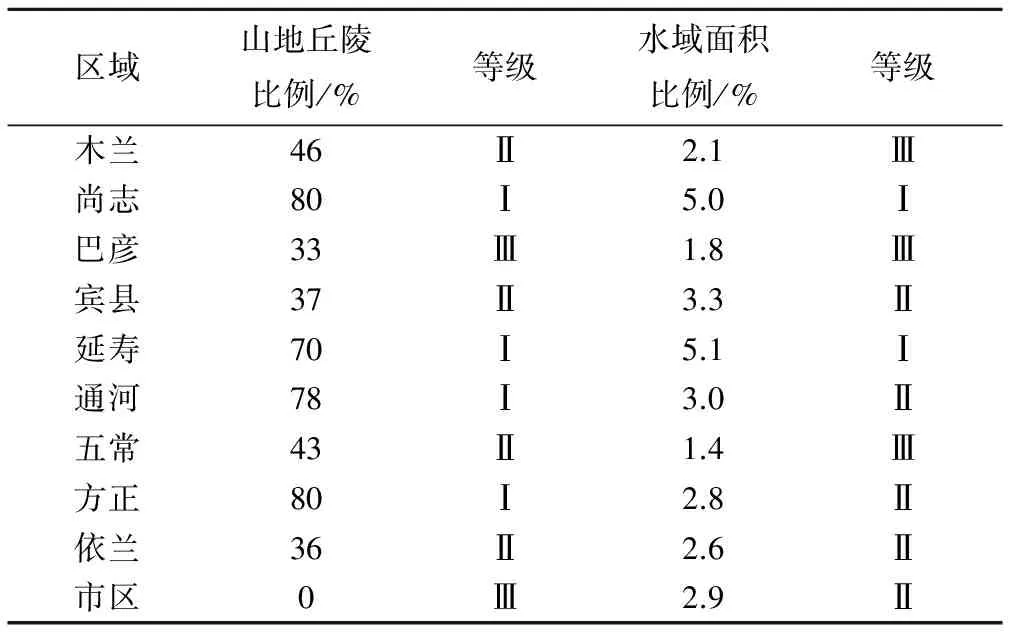
表3 哈尔滨各区域山地和水域面积比例及其分级Tab.3 Average value of proportion of mountain areaand its grade of each county in Harbin

图3 哈尔滨各区域山地面积比例空间分布Fig.3 Spatial distribution of proportion of mountain area of each county in Harbin

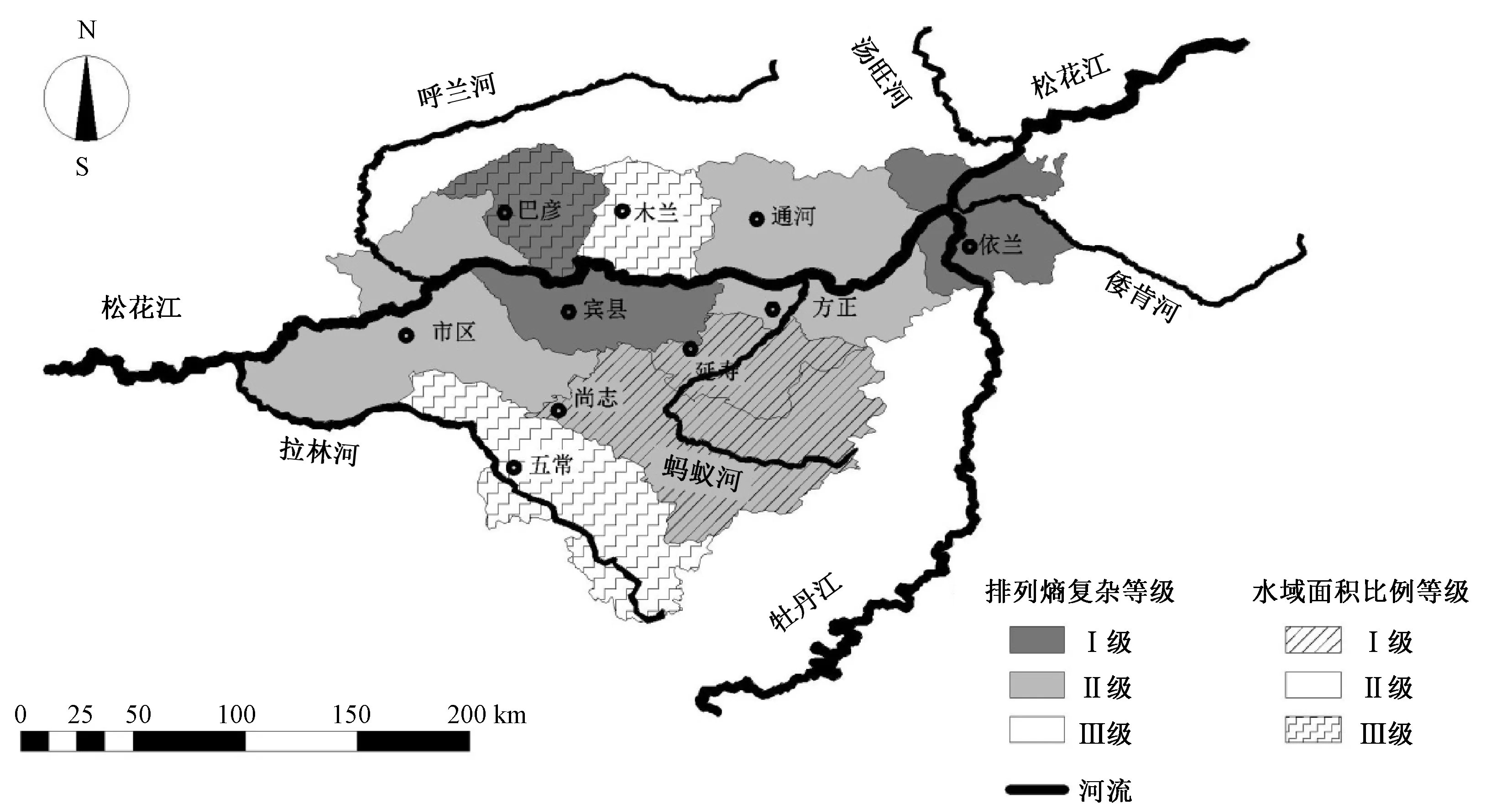
图4 哈尔滨各区域水域面积比例空间分布Fig.4 Spatial distribution of proportion of water area of each county in Harbin

综上所述，哈尔滨地区山地地形与水域对地下水埋深序列复杂性有重要影响，但具有差异性，其中山地地形的影响比水域影响较大一些。因此，下垫面条件对地下水水文系统复杂性有着一定影响。

4 结 论

本文运用PE测度哈尔滨地区2008-2013年地下水埋深序列复杂性，并分析下垫面条件对其影响，结论如下：

(1)PE算法具有计算简便、结果稳定、抗干扰，适用于分析水文水资源复杂性特征。

(2)巴彦、宾县、依兰3个区域地下水埋深序列复杂性为Ⅰ级，说明这3个区域的预测难度大；市区、方正、尚志、通河、延寿5个区域地下水埋深序列复杂性为Ⅱ级，说明这5个区域的预测难度一般；木兰、五常2个区域地下水埋深序列复杂性为Ⅲ级，说明这两个区域的预测较为简单。

(3)巴彦和依兰等5个区域的地下水埋深序列复杂性与山地地形比例等级一致，而巴彦和依兰2个区域的地下水埋深序列复杂性与水域面积比例等级一致，说明当地下垫面条件对地下水水文系统复杂性有重要影响；而其他区域则表现出地区差异型，推测是因为人类活动对地下水水文系统干扰较大。

(4)参数嵌入位数和延迟时间以及数据长度都直接影响着分析结果，所以结合智能算法优化参数以及数据完整收集并结合人类活动影响，对未来的地下水水文系统复杂性影响有重大意义。

[1] 洪 波，唐庆玉，杨福生，等. 近似熵,互近似熵的性质--快速算法及其在脑电与认知研究中的初步应用[J]. 信号处理，1999，15(2)：100-108.

[2] 苟 竞，刘俊勇，魏震波，等. 基于多尺度熵的电力能量流复杂性分析[J]. 物理学报，2014，60(20)：208402(1-8).

[3] 姜 丹, 钱玉美. 效用风险熵[J]. 中国科学技术大学学报, 1994，24(4) ：461-469.

[4] Quian Q R, Rosso O A, Baar E. Wavelet entropy: a measure of order in evoked potentials[J]. Electroencephalography & Clinical Neurophysiology Supplement, 1999,49:299-303.

[5] Ziesche P. Correlation strength and information entropy[J]. International Journal of Quantum Chemistry, 1995,56(4):363-369.

[6] Vasicek O. A Test for Normality Based on Sample Entropy[J]. Journal of the Royal Statistical Society, 1976,38(1):54-59.

[7] Cheng H D, Chen J R. Automatically determine the membership function based on the maximum entropy principle[J]. Information Sciences, 1997,96(3-4):163-182.

[8] 赵小磊, 任明荣, 张亚庭,等. 基于排列熵的心电信号非线性分析[J]. 现代电子技术, 2010,33(19) ：90-93.

[9] 颜云华, 吴志丹. 基于MEMD的高速列车转向架故障的排列熵特征分析[J]. 电子技术应用, 2016,42(5) ：124-127.

[10] 丛 华, 崔 超, 刘远宏,等. 基于排列熵和CHMM的齿轮故障诊断[J]. 失效分析与预防, 2015,(2) ：72-77.

[11] Azami H, Escudero J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application to electroencephalogram recordings [J]. Biomedical Signal Processing & Control, 2016,23:28-41.

[12] Srinu S, Mishra A. Cooperative sensing based on permutation entropy with adaptive thresholding technique for cognitive radio networks [J]. IET Science Measurement & Technology, 2016:1-25.

[13] Xiu Jun L I. The Alkili-saline land and agricultural sustainable development of the western songnen plain in China [J]. Scientia Geographica Sinica, 2000,20(1):51-55.

[14] Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series [J]. Physical Review Letters, 2002,88(17):174 102.

[15] Parra L, Spence C. Cooperative sensing based on permutation entropy with adaptive [J]. IEEE Transactions on Speech & Audio Processing, 2000,8(3):320-327.