土壤水分特征曲线模型参数的非线性传输函数研究

李彬楠，樊贵盛

(太原理工大学 水利科学与工程学院，太原 030024)

0 引 言

土壤水分特征曲线是表述土壤含水率与土壤水吸力间关系的曲线，其实质是表征土壤水的能量与数量之间的关系。土壤水分特征曲线反映了土壤的持水性能和释水性能，可从中了解给定土类的一些土壤水分常数和特征指标。曲线斜率的倒数称为比水容量，是运用扩散理论求解水分运动时的重要参数之一。土壤水分特征曲线在研究土壤水分运动、利用调节土壤水、土壤改良等方面具有十分重要的理论意义和应用价值。中国学者在此领域也做出了突出贡献，于沉香[1](2013年)等在研究盐渍土土壤水分特征曲线时得出拟合盐渍土水分特征曲线的最佳模型是FX模型的结论；谭霄等[2]研究分析了盐分对土壤水分特征曲线的影响，得到随着含盐量的增加土壤水分特征曲线偏移减小，持水性有所降低的结论；赵雅琼[3]等进行了不同粒径下土壤水分特征曲线的测定，研究表明粒径对土壤水分特征曲线的影响是通过土体的孔隙状况来反映的(土壤粒径越小，孔隙结构越密实，中、小空隙增多其连通性变差，土壤具有较高的进气值和良好的持水性能)；高惠嫣[4]等分析了不同土壤质地的土壤水分特征曲线，得到在同一土壤水吸力下，重壤土、中壤土、轻壤土、紧砂土和粗砂土等5种质地土壤的含水率依次下降的结论。

国内外的专家学者在土壤水分特征曲线的实验与模型研究方面也取得了令人瞩目的成就，研究出多个表征土壤水分特征曲线的经验公式，如Brooks-Corey模型[5]、Van-Genuchten模型[6]、Gardner模型[7]、Frdlund and Xing模型[8]等。而在这些模型中，Van Genuchten模型的参数具有适用性好，精度高，物理意义明确等优点而被广泛地应用。肖建英[9]等利用Van-Genuchten模型对砂性漏斗测量中砂的吸湿过程和脱湿过程土壤水分特征曲线进行拟合，实验结果表明拟合效果好；王小华[10]等对传统耕作和免耕耕作两种方式下的土壤水分特征曲线进行分析并建立了相应的Van-Genuchten模型，结果表明Van-Genuchten模型适应性好，可用于不同耕作条件下的土壤水分分析。

纵观以上研究，专家学者的研究都聚焦于土壤水分特征曲线试验和数学模型的表征研究方面，而对多因素、变条件下模型参数研究还鲜有报道。本文基于黄土高原区土壤的水分特征曲线和土壤理化参数系列试验，利用土壤转换函数法理论，在分析土壤理化参数：土壤黏粒含量、粉粒含量、容重、有机质含量、全盐量等对土壤水分特征曲线Van-Genuchten经验模型参数影响的基础上，创建以易测取的土壤常规理化参数作为输入变量，以难获取的土壤水分特征曲线Van-Genuchten模型的参数作为输出变量的土壤传输函数，实现Van- Genuchten模型参数的非线性预报。进而实现对黄土高原区土壤水分特征曲线的预测预报。

1 材料与方法

1.1 试验条件

土壤基本理化参数与土壤水分特征曲线的室内系列试验所用土壤来自于山西省黄土高原区，试验区包括了山西省5个县(市、区)，分别为晋中市的榆社县、介休市和吕梁市的交城县、临县、离石区。通过土壤理化参数试验测定，试验区的土壤主要为壤土，包含粉砂质黏壤土、砂质壤土、粉砂质壤土等多个类型，土壤基本理化参数分布范围如下：黏粒量取值范围是0.01%～17.54%；粉粒量取值范围是31.73%～63.30%；干容重取值范围是0.94～1.95 g/cm；有机质含量的取值范围是1.8～27.4 g/kg；无机盐含量的取值范围是0.682 3～2.269 1 g/kg。

试验区土壤其质地类型、容重、有机质和盐分含量具有明显变化，包含了多种土壤理化参数指标及其土壤状况，类型多种多样，所建立的样本数据库代表性强，每一个县(市)取一个典型试验点，其土壤理化参数情况见表1。

表1 试验区内各项土壤理化参数表

1.2 实验方案

(1)试验内容。

不同土壤条件下土壤水分特征曲线及其模型参数。

与土壤水分特征曲线相对应的理化参数土壤质地、土壤容重、土壤有机质含量、土壤盐分的含量测定。

(2)试验设计。

通过变条件(不同土壤质地、结构、有机质含量、盐分含量)下的土壤水分特征曲线及与土壤水分特征曲线相对应的理化参数土壤质地、土壤容重、土壤有机质含量、土壤盐分含量测定，获取土壤水分特征曲线模型参数和土壤理化参数指标。变土壤条件考虑与设计如下：

土壤质地：根据试验区内15个试验点的质地进行试验，试验点取土深度为0～20和20～40 cm。确保样本的多样性。

土壤容重：本试验的土样为扰动土，需人为配制不同的土壤容重，设计10个梯度的容重，分别为1.0、1.1、1.2、1.3、1.35、1.4、1.45、1.5、1.6、1.7 g/cm3，基本涵盖了黄土高原区土壤容重的变化范围。

压力级差：在进行单条土壤水分特征曲线时，人为设计不同的压力值等级：3、6、10、30、60、80、120、150 m，共8个水平，确保土样能够在不同的压力值下充分排水。

土壤有机质含量：设计值随选定的试验土壤质地值而变，测量深度为0～20 cm和20～40 cm两层。

土壤含盐量：设计值随选定的试验土壤而定，测量深度为0～20 cm和20～40 cm两层。

(3)试验仪器与方法。土壤水分特征曲线试验：使用美国制造的1500F型压力膜仪进行测定。具体方法如下：先将自然风干的试验用土土样过1 mm筛，然后装在高1 cm体积为20 cm3的环刀中，环刀与土样的上界面保持齐平。其次把环刀放到压力膜仪中的陶土板上并加入适量的水，确保土样吸水达到饱和，过24 h后测定土样的饱和含水率。随后对土样进行加压：按0.3、0.6、1 bar等不同的压力值逐一加压，最大压力值为15 bar。在此过程中，受到压力作用的土样开始通过排水系统将水排出。每隔相同的时间进行土样重量测定，如果前后两次的重量差小于0.005 g，说明在该压力下土样水分全部排出，可对下一个压力等级进行测定。在测定完所有压力值后烘干土样并测出其干容重值，通过计算不同压力等级下土样的体积含水率，从而得到不同水吸力下的土壤含水率，最后通过MATLAB软件拟合得到土壤水分特征曲线相应的模型参数。

土壤理化参数试验：本文建模所涉及的土壤理化参数主要有土壤质地、土壤容重、土壤有机质和含盐量等。对于土壤质地的测定采用激光粒度分析仪进行黏粒、粉粒、砂粒的含量测定；土壤容重的测定采用环刀法进行；有机质含量采用重铬酸钾容量法进行测定；对于盐分的测定，本试验用K+、Na+、Mg2+、Ca2+、SO2-4、CO2-3、HCO-3、Cl-八大离子含量来代表土壤中盐分含量，采用化学法和火焰光度计进行测定。

1.3 土壤水分特征曲线模型与数据样本

(1)土壤水分特征曲线模型。本文将针对水分特征曲线Van-Genuchten经验模型参数进行预测，其模型机构如下：

(1)

式中：θ是体积含水率；θs为饱和含水率；θr为残余含水率，m3/m3；h为压力水头，m；α是与进气值有关的参数，m-1；m、n是曲线形状参数，m=1-1/n。参数n表征曲线坡度的陡缓情况，参数α是表征土壤的进气值大小。尽管Van-Genuchten模型参数有4个，但是饱和含水率与参与含水率可以通过较为简单的实测试验获得，参数α和n作为经验参数不能通过试验获得，故采用土壤传输函数法来获取，由此确定的输出参数为α和n两个。

(2)Van-Genuchten模型参数与理化参数样本。本文所涉及的试验取土范围覆盖山西省五个县(市)的耕作农田，各类土壤理化参数分布差异性大，土壤丰富多样，对土壤水分特征曲线Van-Genuchten模型参数进行预报的代表性强。通过土壤水分特征曲线室内试验最终得到土壤水分特征曲线的样本数据，并利用RETC和MATLAB软件分析拟合了各组土壤水分特征曲线，得到Van-Genuchten模型中的4个参数，对Van-Genuchten模型参数α和n的预报提供支撑。拟合数据如下：

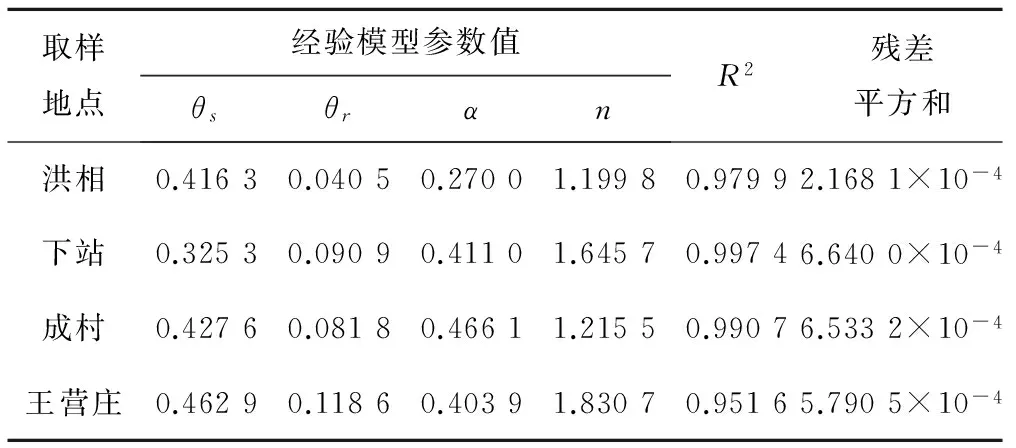
表2 Van-Genuchten经验模型参数表

从试验区随机选取的不同地域的土壤，其相关系数R2的值均在0.95以上，且残差平方和均较小，说明利用Van-Genuchten模型表征山西省试验区各类土壤的拟合效果好。

(3)数据样本。通过土壤水分特征曲线和理化参数试验，最终得到93组土壤基本理化参数与Van-Genuchten模型参数样本，使用85组试验样本建立非线性预报模型，8组作为检验样本。85组土壤基本理化参数与Van-Genuchten模型参数代表性样本见表3。

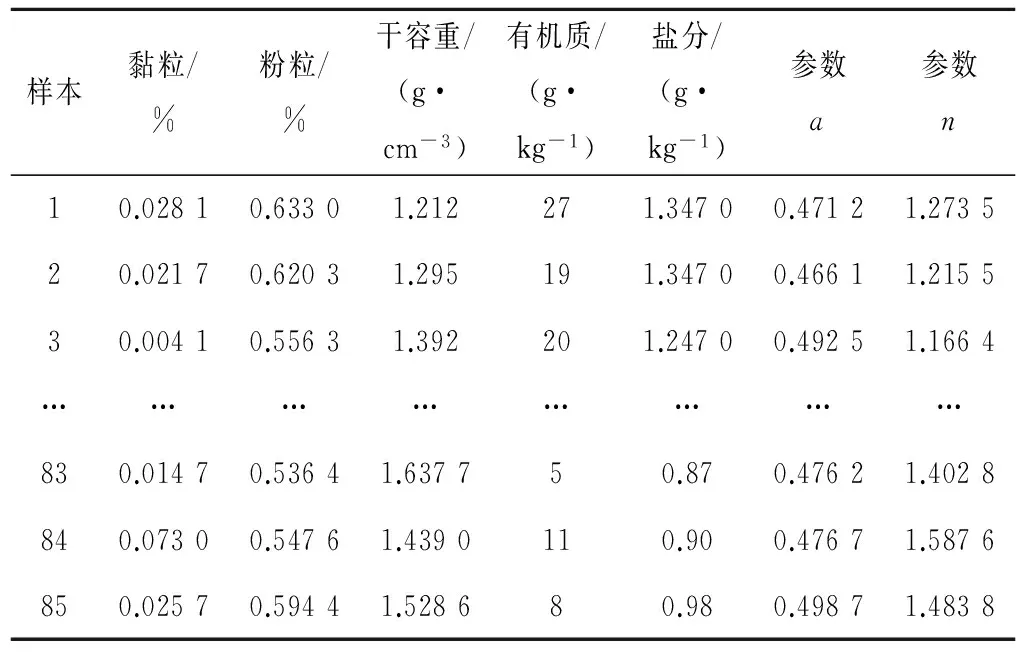
表3 土壤基本理化参数与模型参数

2 土壤基本理化参数对Van-Genuchten模型参数的影响分析

通过土壤水分特征曲线系列试验，利用EXCEL和MATLAB工具箱中的CFTOOL软件进行土壤理化参数和模型参数之间的单因素影响分析，发现土壤基本理化参数如土壤质地、干容重、有机质含量、盐分含量对Van-Genuchten模型参数α和n的影响较大，其机理分别表现在：

土壤质地状况的差异会导致土体孔隙状况的不同，土壤水分特征曲线因此而改变特性。随着黏粒含量的增加土壤质地逐渐变重，土壤吸持水能力增强，从而增加了土壤初始排水的难度，参数α的值随进气吸力值增大而减小，同时黏粒含量增加使同一吸力下的土壤含水量增多，土壤水分特征曲线向右偏移且坡度变缓，参数n也随之减小，因此Van-Genuchten模型参数α和n均随着黏含量的增加而减小。

土壤干容重通过土壤孔隙状况的变化影响土壤水分特征曲线的性质，土壤干容重增加，导致大孔隙的数量减小，中小孔隙的数量增多，因大孔隙持水量减少而中小孔隙持水量增加，使得土壤结构密实，初始排水难度增加，从而Van-Genuchten模型参数α和n随之减小。

土壤有机质通过土壤结构和土壤胶体状况的改变对土壤水分特征曲线产生影响，这两个方面使得土壤吸附水分的能力增强，从而土壤需要更大的压力值排出水分，因此Van-Genuchten模型参数α和n随之减小。土壤盐分含量的增多提升了土壤吸持水能力，因此Van-Genuchten模型参数α和n会随之减小。

参数α表征土壤初始排水时的难易程度，其受到包括土壤质地、结构、有机质和盐分含量等的综合影响，因此参数α以W1(黏粒含量)、W2(粉粒含量)、γ(干容重)、G(有机质)、ψ(盐分)这5个变量为非线性预报模型的输入参数；参数n表征土壤水分特征曲线的坡度状况，其与土壤结构、土壤质地、胶体状况等密切相关，因此参数n的非线性预报模型以W1、W2、γ、G、ψ5个变量为输入参数，与参数α一致。

如前所述Van-Genuchten模型参数有4个，由于残余含水率与饱和含水率可通过实测实验获得，但经验参数α和n不能通过实测实验获得，因此采用土壤传输函数法获取，由此确定参数α和n为输出参数。

3 Van-Genuchten模型参数土壤传输函数的建立

3.1 单因素函数关系确定

单因素函数关系的确定采用统一变量法，即保证其他的土壤基本理化参数相近或相同，只考虑自身单因素对Van-Genuchten模型参数α和n的影响，其具体函数关系式见表4。

表4 Van-Genuchten模型参数与土壤基本理化参数单因素函数关系

由表4可知，参数α和参数n与黏粒含量W1、粉粒含量W2均呈线性关系，参数α与干容重γ呈对数关系，参数n与干容重γ呈线性关系，参数α与有机质G呈指数关系，参数n与有机质G呈对数关系，参数α和参数n与盐分含量均呈对数关系。

3.2 多元非线性模型结构确定

多元非线性模型是将各个单因素形式进行机械叠加，确定多个输入参数与输出参数的多元非线性形式，由此得到参数α和n与土壤基本理化参数之间的关系，具体形式如下：

α=β0+β1W1+β2W2+β3ln(γ)+β4eG+β5ln(ψ)

(2)

n=β0+β1W1+β2W2+β3γ+β4ln(G)+β5ln(ψ)

(3)

3.3 非线性模型系数的确定

基于建模样本，利用MATLAB软件，对式(2)和(3)进行拟合并计算各个输入参数的系数值，最终求出多元非线性函数关系式，如下：

α=0.054 1-2.511W1-0.297 3W2-0.066 5 lnγ-

0.656 6eG-0.256 4 ln(ψ)

(4)

n=2.840 4-2.511W1-1.843 3W2-0.213 5γ-

0.035 7 ln(G)-0.418 2 ln(ψ)

(5)

3.4 模型自变量T检验

利用MATLAB软件中的T检验程序，对最后求出的多元非线性函数关系进行T检验，要求自变量检验|T|≥T0.05/2，即|T|≥2.014 4，满足此条件则T检验合格，最终确定非线性预报模型的所有输入参数，参数α和参数n的输出参数T检验表见下。

表5 参数α回归方程自变量T值检验表

表6 参数n回归方程自变量T值检验表

经过T检验分析，影响Van-Genuchten模型参数的各土壤基本理化参数均通过T检验，且|T|均大于2.014 4，可以确定参数α的输入参数是W1、W2、ln(γ)、eG、ln(ψ)，参数n的输入参数是W1、W2、γ、ln(G)、ln(ψ)，因此最终确定参数α和参数n的非线性预报模型，如上式(4)和(5)所示。

3.5 非线性预报模型显著性F检验

对建立模型的85组样本进行非线性预报模型显著性检验，通过MATLAB软件中的程序求出预报模型的F值，并与给定显著水平α下相应的F0.05的值进行比较，最终判定非线性预报模型整体的显著性，比较结果见表7。

表7 非线性预报模型F值检验表

从表7中可以看出，参数α和参数n的非线性预报模型均通过F检验，说明建立的非线性预报模型显著性高，由其建立的Van-Genuchten模型参数α和n的预报具有较好的可信度。

3.6 建模样本与验证样本分析

将85组建模样本的实测值与预报值以及相对误差值列于表8。由表8可知，参数α建模样本的平均相对误差为9.66%，参数n的平均相对误差为6.83%，建模精度较高，说明利用土壤基本理化参数来预报Van-Genuchten模型参数α和n的土壤传输函数法是准确可行的，可用于土壤水分特征曲线模型参数的预报。

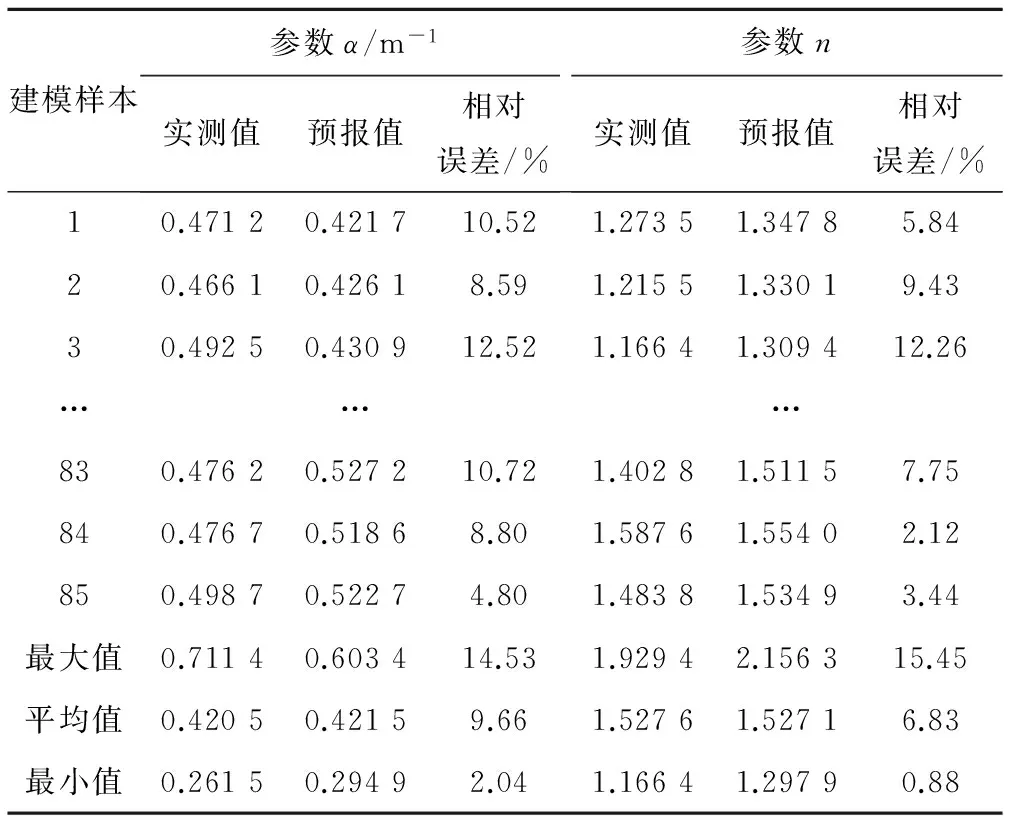
表8 非线性建模样本精度表

将8组验证样本代入所建的非线性预报模型，得到每一组样本的预报值，并求出相对误差，，验证样本的误差值见表9。

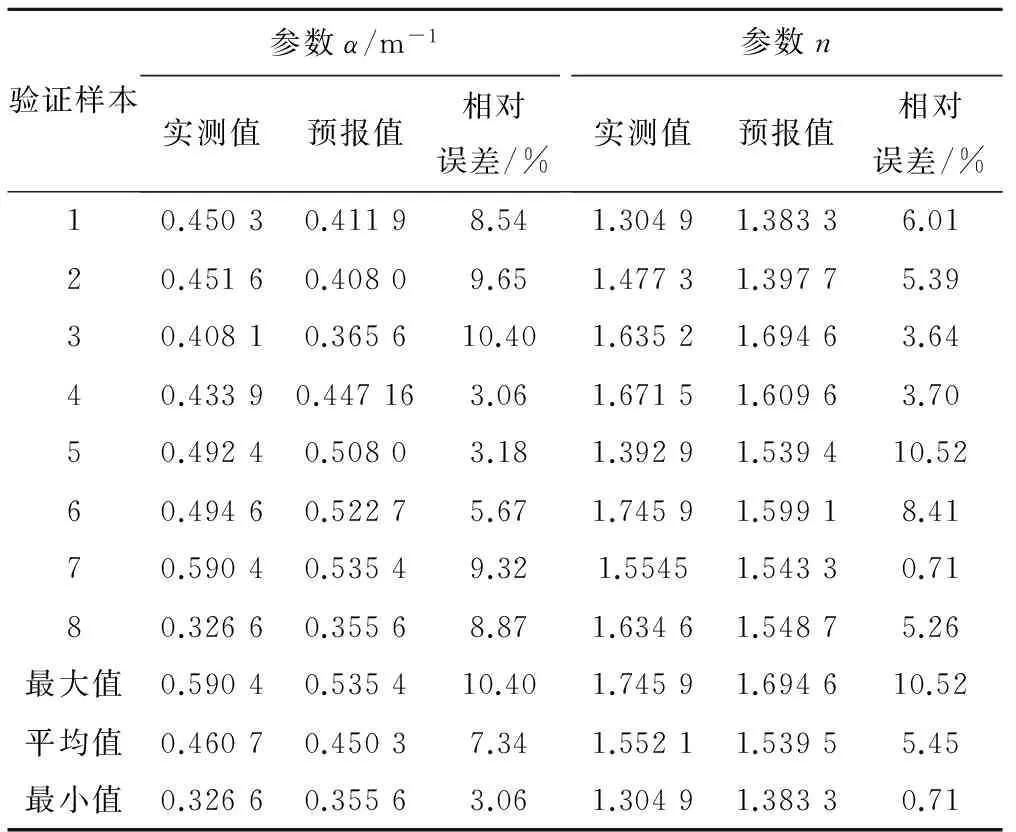
表9 非线性验证样本精度表

从表9可知，验证结果显示参数α的平均相对误差为7.34%，参数n的平均相对误差为5.45%，检验样本的误差比建模样本更小，且均低于10%。这表明：用所建土壤传输函数模型进行Van-Genuechten模型参数α和n的预报精度较高，可以用来预测土壤水分特征曲线的形状参数，为土壤水分特征曲线模型参数的预报提供支撑。

4 结 论

⑴基于土壤黏粒含量、粉粒含量、干容重、有机质含量、盐分含量所建的Van-Genuechten模型参数α与n的非线性预报模型是可行的，其平均相对误差低于10%，在可接受范围内。

⑵从Van-Genuechten模型参数α和n的多元非线性预报的精度来看，参数α的建模样本相对误差的平均值为9.66%，参数n的建模样本相对误差的平均值为6.83%，说明该模型的建模精度较高；同时8组验证样本中参数α的相对误差的平均值为7.34%，参数n的相对误差的平均值为5.45%，验证样本比建模样本具有更好的预报精度，说明建立的非线性预报模型能够较好地实现对土壤水分特征曲线模型参数的预报。

⑶以土壤基本理化参数为输入参数，Van-Genuechten模型参数α和n为输出参数的土壤传输函数法是可行的，且非线性预报模型形式简单，物理意义十分明确。通过建立土壤理化参数与土壤水分特征曲线之间的预报模型，为黄土地区获取土壤水分特征曲线的途径提供了理论与实例支撑。

[1] 于沉香,张虎元.盐渍土土水特征曲线测试及预报[J].水文与工程地质.2013,40(2):113-118.

[2] 谭 霄，伍靖伟，李大成，等.盐分对土壤水分特征曲线的影响[J].灌溉排水学报，2014，33(4/5):228-232.

[3] 赵雅琼,王周锋，王文科. 不同粒径下土壤水分特征曲线的测定与拟合模型的研究[J].中国科技论文,2015,10(3):287-290.

[4] 高慧娟，杨路华.不同质地土壤的水分特征曲线参数分析[J].河北农业大学学报，2012,(5).

[5] Brooks R H,Corey A T. Hydraulic properties of porous media[J]. Colorado States University Hydrol, 1964,(3): 27.

[6] Van Genuchten R. Predicting the hydraulic conductivity of unsaturated soils[J]. Soil Sci. Soc. Am.J., 1980,44:892-898.

[7] Garder W R, Hillel D·B Y. Post irrigation movemwnt of soil water I Redistribution [J]. Water Resocurce Research, 1970s,6:851-861.

[8] Fredlund D G, Xing A. Equations for the soil-water characteristic curve[J].Can.Geotech.J.,1994,31:521-532.

[9] 肖建英，李永涛，王 丽.利用Van-Genuchten模型拟合土壤水分特征曲线[J].地下水，2007,29(5):46-47.

[10] 王小华，贾克力，刘景辉，等. Van-Genuchten模型在土壤水分特征曲线拟合分析中的应用[J].干旱地区农业研究，2009,27(2):179-183.