农业灌溉用水补偿博弈研究

邢夏洁，袁汝华

(河海大学商学院，南京 211100)

0 引 言

我国农业水价改革一直是关系到农民切身利益和国家农业发展的重要问题。水价调整的主要方向是保证供水单位的正常经营和充分考虑农民的支付能力，逐步将现行水价提升至供水成本。然而长期以来，农业灌溉用水水价低廉，不足成本的一半，农户水权意识薄弱，水费实收率低，且2006年国家对农民免征农业税，这一方面激发了农民的生产积极性，但是另一方面更是增加了水费征收的阻力，因为农民认为“皇粮税”都免了，为何还要交水费？近年来，随着粮食要素成本的不断上升，而粮食价格却相对稳定，粮食收益很低，农民的生产和生活面临很大的经济压力，承受能力很低。种种原因都阻碍了水价的调整，因此，为了减轻农民负担，提高水费实收率，合理的水费补偿政策是很有必要的。对此很多学者开展了相关研究。

在农业水费补贴模式上，尹庆民对此进行了详细的研究，用经济学的方法比较了财政全额补贴、直补灌区和直补农户这三种水费分担模式，得出了对农户进行直接补贴较为有效的结论，指出此模式在增加消费者福利的同时也节约了水资源[1]。刘红梅表示从国内外的经验来看由暗补到明补是一种必然的趋势，提出在我国当前过渡时期，采取有限制的暗补对全社会来说是一种帕累托改进[2]。在水费补贴机制上，田贵良学者同样主张采用明补的方式直接对农民发放财政补贴，他还设计了农业水费补偿机制的流程和构建了补偿机制的基本框架[3]。在农业水价补贴额度上，马孝义首先基于帕累托优化对农业水价定价机制进行了分析，接着建立了政府直补农民的水价定价模型，并举例计算出了陕西省关中地区的政府直补农户的定额[4]。杜丽娟在分析比较了4种水价模式之后，建议财政先对供水单位进行政策性亏损补贴和对农户在灌溉定额内的用水进行补贴，超出定额之外的，农户负担计量水价。在进行了财政直接补贴农业水费的供求分析之后，给出了全国水费补贴需求总额[5]。

本文从博弈论的角度对农业水价补偿问题进行分析，通过推导给出理论上政府水费补偿模型，并提出在水价升高政府给予补偿后，当节水效益未达到一定程度仍然存在囚徒困境的情形，即农户基于自身利益最大化依旧选择不节水，此时需要政府的干预和引导，由此完善水费补偿问题的研究。

1 水价补偿博弈模型

1.1 博弈论

博弈是一些个人或者组织，在一定的环境条件下，共同遵守一定的规则，同时或者先后做出策略选择并得到一定结果的过程[6]。而博弈论是研究策略、计谋和决策问题的工具。它能够系统的分析博弈过程中博弈双方相互制约、相互依存的规律，寻求双方合理的策略选择和结果并用以说明相应的实际问题。运用博弈论可以用来指导经济、政治等方面的决策活动。

博弈的结构通常包含4个方面的核心内容：博弈方、策略集、次序和得益。

博弈通常表示为：

G={S1,…,Sn；u1,…,un}

式中：G表示一个博弈，例如，有i个博弈方参与了此次博弈；Si是策略空间，即每个博弈方可选策略的集合；ui为第i个博弈方的得益。

根据博弈方数量的多少可将博弈分为单人博弈、双人博弈和多人博弈，根据得益的总和不同分为零和博弈、常和博弈与变和博弈。根据决策过程的先后顺序分为静态博弈、动态博弈。而在博弈中博弈双方对信息的掌握程度对整个博弈过程起到至关重要的作用，根据对信息的掌控程度可将博弈分类。博弈方完全了解所有博弈方在各种情况下收益的博弈称为完全信息博弈，否则称为不完全信息博弈。在动态博弈中，将各博弈方完全了解所有博弈方的策略选择进程的博弈称为完美信息的动态博弈，否则称为不完美信息的动态博弈。

1.2 政府与农户之间的水价补偿博弈

在农业水价尚未改革之前，农民一直享受着低廉的水价，对“水是商品”这一认识不足，水权意识薄弱，且由于水费实收率低，供水单位经营举步维艰，灌区没有能力进行供水工程的维修和改造，灌溉工程配套设施不全面，用水计量设施不足，无法准确测量用水量，导致农民节水意识淡薄，水资源利用率不高，浪费宝贵的水资源。现提高水价之后，且考虑到农民的承受能力给予一定的水费补偿，这样一来，供水单位能够正常经营，农民节约了灌溉用水，水资源得到了合理的配置，社会总效益提高，获得了一定的帕累托改进，节约的用水量进一步考虑水权转让或进行生态建设将增加更多的社会福利。农民节水和不节水与政府制定低价水费及在制定高价水费时给予农户补偿存在着博弈，为了更好阐述水价补偿博弈模型，先对模型中出现的符号进行含义说明。

1.2.1 符号说明与模型构建

(1)对博弈模型中出现的符号具体作如表1说明。

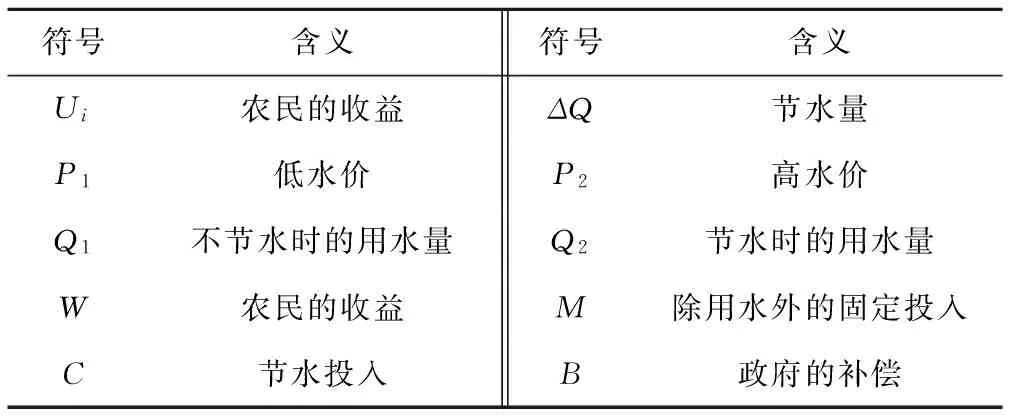
表1 符号说明Tab.1 Symbol definition

(2)基本假设与模型构建。在此次博弈中，博弈方为政府和农民，政府的策略集为制定低价格的水费P1或者高价格的水费P2(P1Q2。W为农民出售农产品所获得的收入，假设市场农产品价格保持稳定且农民是否进行节水灌溉并不影响农产品的产量，因此农民所获的收入不变。M为除灌溉用水之外的其他生产要素的固定投入。C是为了节水投入的固定成本(如节水技术改造费、末级渠系基础设施改造费等)。B为政府在采取高水价时对农民灌溉用水的补偿。在此博弈模型中，主要关注的是农民的收益函数，最终通过模型的求解得到政府对农民高价用水的补偿费用。假定农民为完全理性的经济人，追求自身经济利益的最大化，博弈双方的收益矩阵如表2所示。

表2 政府与农民的收益矩阵Tab.2 Payoff matrix between government and farmer

基于以上假设可求得农民在各种情况下的收益函数：

U1=W-P1Q1-M

(1)

U2=W-P1Q2-C-M

(2)

U3=W-P2Q1-M+B

(3)

U4=W-P2Q2-C-M+B

(4)

当政府采取低水价(P1)策略制定水费时：

U2-U1=P1Q1-P1Q2-C=P1(Q1-Q2)-C

(5)

此时水价很低，节水技术费用较高，节水带来的效益不足以弥补节水灌溉的投入，因此U2-U1<0，农民在水费较低时自然会选择不节水灌溉。

当政府采取高水价(P2)策略制定水费时：

U4-U3=P2(Q1-Q2)-C

(6)

水价很高时，节水带来的收益可以抵消节水灌溉的投入，则U4-U3>0，即：

P2ΔQ>C

(7)

最终农民会选择在高水价时节水灌溉。

对于完全理性的农民来说，政府采取高水价策略农民进行节水灌溉的收益要大于低水价不进行节水灌溉的收益时，农民才会甘愿接受在高水价时节水灌溉，否则水价提高会引起农民的不满。因此U4>U1，即：

W-P2Q2-C-M+B>W-P1Q1-M

(8)

整理可得：

B>P2Q2-P1Q1+C

(9)

要求得政府补偿额度B的范围，则转换为求：

B>max(P2Q2-P1Q1+C)

(10)

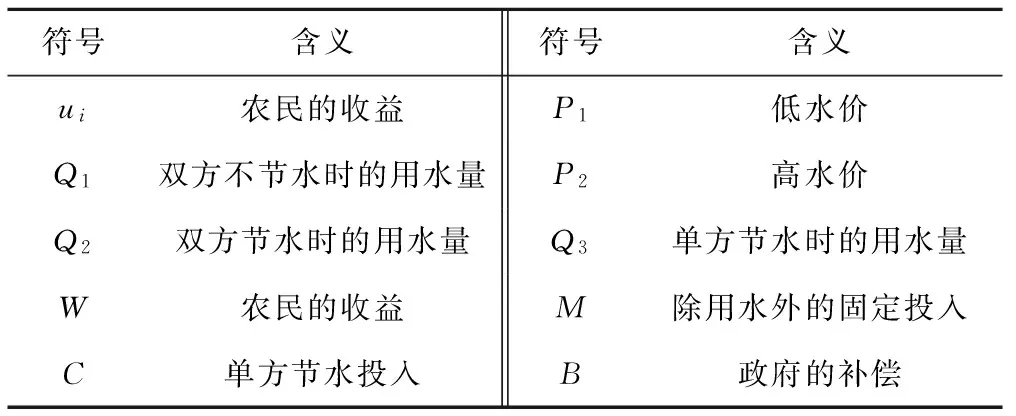
由式(7)C

B≥P2Q2-P1Q1+P2ΔQ

(11)

最终可得：

B≥P2Q1-P1Q1

(12)

即：

B≥ΔPQ1

(13)

求得政府在高水价补偿农民的最小支付额度：

Bmin=ΔPQ1

(14)

1.2.2 博弈分析

从以上博弈过程可以看出，水价提高时可促使农民节水，但考虑到农民承受能力，要想使农民心甘情愿的在高水价时自发地进行节水灌溉，必须要给予一定的财政补贴。补偿额度B可以分解为两部分内容，一部分是ΔPQ2(水价提高之后农民用水量已经从Q1降低至Q2)，即每单位农业用水农民实际支付水费与实际水价之间的差额乘以实际用水量，将这一部分的补偿理解成用水补偿额度。该额度的补贴保证了农民的每单位用水量的实际支付水费仍然是未提价前的水价水平。另一部分为:

ΔPQ1-ΔPQ2=ΔPΔQ

(15)

将这一部分补偿理解为节水补偿额度，也可视为是一种节水奖励。它表示根据农民节水量的多少给予相应的水价差额补贴，这一部分的补偿可激励农民自发节水。

我们也可以从另一角度来分析理解节水补偿额度。假设农业灌溉用水财政补贴只有用水补偿额度ΔPQ2，农民在高水价时节水的效益U4变为U′4：

U′4=W-P2Q2-C-M+ΔPQ2

(16)

此时,用低水价不节水时农民的效益减去高水价时政府只补贴用水补偿额度的农民效益得到：

U1-U′4=P1Q2-P1Q1+C=C-(P1Q1-P1Q2)=C-P1ΔQ

(17)

式(17)表示节水成本投入与在低水价时节约的水资源价值之差。由上文分析可知，当水价很低时，节水所获得的收益不足以抵消节水成本投入,因此政府还应该补偿这一部分由于节水而带来的效益损失，或者称之为对其节水的奖励。由式(7)C

C-P1ΔQ

(18)

即:

U1-U′4<ΔPΔQ

(19)

说明此时必须再补偿ΔPΔQ才能确保农民在高水价时节水的收益始终高于低水价不节水时的收益。

此时得到的政府总补偿额度ΔPQ2既包含了用水补偿额度又涵盖了节水补偿额度。既提高了农民的承受力又激励农民自发主动的节约水资源。在当水价提高时，获得农业灌溉的用水量便能求得政府应当支付农民的总额度。

1.3 农户与农户之间的博弈

假设如上文所述，政府在高水价时对农户进行了ΔPQ2的补偿，作为完全理性经济人的农户是否一定会选择在高水价时节水呢？下面本文将考查农户与农户之间的博弈来研究这一问题。

1.3.1 符号说明与模型构建

(1)对博弈模型中出现的符号具体作如下说明。

表3 符号说明Tab.3 Symbol definition

(2)基本假设与模型构建。假设有两家种植规模相当的农户A和农户B，双方的策略依旧是节水灌溉或是不节水灌溉，他们共用相同的节水灌溉技术(如渠系防渗)，双方为此共同支付2C，当一方进行节水投入，另一方不投入时，双方依旧都能节水，节水的用水量为Q3，且Q2Q2)。农户与农户之间的博弈收益矩阵如表4所示。

表4 农户与农户的收益矩阵Tab.4 Payoff matrix between farmers

基于以上假设可求得农民在各种情况下的收益函数，如下文所示：

u1=W-P2Q1-M+B

(20)

u2=W-P2Q2-M-C+B

(21)

u3=W-P2Q3-M-C+B

(22)

u4=W-P2Q3-M+B

(23)

因为Q2u3,u4>u1,u4>u3。

u2-u1=P2(Q1-Q2)-C

(24)

由式(7)可知，P2ΔQ>C，那么u2-u1>0, 得到:

u2>u1

(25)

即双方都节水时的收益大于双方都不节水时的收益。

假设Q3=(Q1+Q2)/2,则：

u4-u2=u1-u3=P2(Q2-Q1)/2+C

(26)

由式(7)可知，P2(Q1-Q2)>C,得:

(27)

此时令α=C/ΔQ，α为节水效益。

当节水效益：

(28)

式(26)大于0,即u4>u2且u1>u3。此时对于农户A来说，农户B有节水和不节水两种策略选择，假设农户B选择节水，收益函数为u2或u3，对农户A来说，选择不节水时获得的收益要大于节水时的收益(u4>u2)，因此农户A选择不节水。假设农户B选择不节水，收益函数为u4或u1，此时对农户A来说，选择不节水时获得的收益要大于节水时的收益(u1>u3)，因此选择不节水。农户A在农户B无论做出何种决策时都选择不节水。对农户B来说情况也相同，不节水也是唯一合理的选择。最终双方都选择不节水，最终双方收益为u1，然而双方都节水的收益是大于不节水的收益的(u2>u1)，此时双方都不愿单独改变自身的策略选择，由此可见，虽达成了纳什均衡，却形成了囚徒困境的局面。

当节水效益非常高时，每单位的节水效益小于水价的一半时，即：

(29)

式(26)小于0,即u4

1.3.2 博弈分析

由上述这一非合作博弈过程可以看出个人理性与集体利益最大化相矛盾，说明“看不见的手”并不是常常有效的，追求个人利益的最大化并不一定使社会福利最大化，此时政府必须对经济活动进行协调工作，对博弈双方进行干预，及时互通信息。现实意义表现为，政府应该向农民倡导节水观念，普及水权意识，阐明水资源价值，传达合理的灌溉模式，只有共同节水才可实现双方共赢。最终达成实现水资源可持续合理利用，加快建设节水型社会的目标。当水权制度不断完善，水市场健全的前提下，农业灌溉节约的水量可转移给其他用水主体，农户可获得额外的补偿和更大的节水激励。

2 实证分析

以黑龙江某县一提水灌区为例，计算财政补贴农业灌溉用水额度。2014年，该灌区面积约为833.3 hm2，灌溉用水量为1 030 万m3,现行农业水价为0.024 2 元/m3。现该县进行农业水价改革，对水价进行重新核算，实际供水成本水价为0.081 元/m3。假设该地区的农业用水需求弹性系数为0.5，建立农业灌溉用水需求与价格的函数关系[4]：

Q′S=QSd-Es

当提价系数d取3.35(P2/P1)时，则次年农业灌溉用水量Q′S=1.03×(3.35)-0.5=560 万m3。此时政府对农户灌溉的最低补偿总额为58.5万元。其中用水补偿额度为31.8万元，节水奖励额度为26.7万元。共节约水资源470 万m3。若将节约的水资源进行水权转让将实现更大的社会效益。假设水价提高之后当地农户由于节水带来的效益增量可以抵消节水投入，即用于节水的投入不足38.07万元(P2ΔQ)，由此可见，无需财政再支付38.07万元用于投入末级渠系的基础设施改造或是补贴农户节水技术改造费，只需投入26.7万元的节水奖励费用便能使农户自发主动的投入节水成本来节约水资源，节省了一定财政补贴费用的投入，减轻财政收入的负担。

当水价提高到实际供水成本水价时，该县政府对农户总共补偿58.5万元。假设农户用于节水的总投入为30万元，由式(28)可知，此时的节水效益0.063 8 元/m3，大于0.040 5 元/m3，说明仍存在囚徒困境的状况，即农户很有可能会选择不节水，因此需要政府进行干预协调，培养农户水权意识，教育农户只有共同节水、选择合作才可实现高收益。由于长期以来农业灌溉采用粗放型的灌溉方式，且节水技术落后，节水效益在短期内不会有大幅度的提高，假设随着节水技术不断地发展进步，采用先进的节水技术，使得农户的节水效益提高70%时，此时农户用于节水的总投入为19万元，此时的节水效益0.040 4 元/m3，小于0.040 5 元/m3，那么将不存在囚徒困境的局面，此时农户会自发进行节水。

3 结 语

本文采用博弈论的方法对农业用水补偿问题进行了分析，由政府与农户之间的博弈模型得到了财政补偿农民用水的额度，并分析了该补偿额度的内涵，该补偿额度由用水补偿额度和节水补偿额度两部分组成。用水补偿额度主要用于补偿由于水价提高农民因此多负担的水费。节水补偿额度主要用于激励农户节水。由农户与农户之间的博弈模型得到了当水价提高时，节水效益并未达到一定程度时，依旧会存在“囚徒困境”的局面，农户可能依旧选择不合作，双方都不愿进行节水投入。此时需要政府开展组织协调工作，倡导节水意识，普及相关知识，充分排解农民的疑虑和困惑，只有共同节水才能实现双方共赢。

本文从理论上对农业水价补偿问题进行了研究，但未考虑中央和地方实际财政收入情况，实证研究不足。本文理想化的将补贴全部“明补”给农民，而从目前财政补贴农业水费现状来看，将财政补贴费用全部直补农民而不补贴供水单位也是不切实际的。“明补”和“暗补”将共存很长一段时间，那么政府对双方的补偿模型有待进一步讨论，且农业用水补偿机制和水权转让机制如何与补偿费用配套也有待进一步的研究。

[1] 尹庆民,马 超,许长新.中国流域内农业水费的分担模式[J].中国人口·资源与环境,2010,20(9):53-58..

[2] 刘红梅,王克强,黄智俊.农业水价格补贴方式选择的经济学分析[J].山西财经大学学报,2006,28(5):81-85.

[3] 田贵良,孙兴波,石常峰,等.农民减负与节水激励双重约束下我国农业水费补偿机制设计[J].价格理论与实践.2014,(2):57-59.

[4] 马孝义,赵文举.基于帕累托优化的农业用水定价机制与模型研究[J].科技导报,2006,24(10):50-53.

[5] 杜丽娟,柳长顺.财政直接补贴农业水费研究[J].资源科学,2008,30(11):1 741-1 746.

[6] 谢识予.经济博弈论[M]. 3版.上海:复旦大学出版社，2006:19-37.