5种砂土水分特征曲线的测试分析
2017-03-21邓宏凯周林康
邓宏凯,周林康,晋 华
(1.太原理工大学水利科学与工程学院,太原 030024;2. 太原碧蓝水利有限公司,太原 030024)
土壤水分特征曲线是表征土壤基质吸力与含水率的关系曲线,它被广泛应用于作物生长研究、径流量与蒸发量计算、土体强度分析以及土壤湿热迁移研究等领域[1,2]。近年来学界对于不同类型的土壤水分特征曲线进行了广泛研究,且多采用试验测定与模型验证相结合的方法进行分析。刘小文研究了红土水分特征曲线,表明基质吸力与含水率呈对数关系,其拟合公式为:ω=a+bln (ψ+c)[3]。付丛生研究了珠江三角洲地区砂土与沙壤土水分特征曲线,得出Gauss函数、Dose response (Bi-dose response)函数对其拟合效果良好[4]。孙迪研究了长白山阔叶红松林土壤水分特征曲线,得出利用Gardner公式对其进行拟合的效果良好[5]。郑荣伟研究了北京通州区典型农田土壤水分特征曲线,得出Van Genuchten模型对其拟合效果较好[6]。姚姣转研究了科尔沁沙地土壤水分特征曲线,构建了土壤基本参数与水分特征曲线之间的传递函数,并验证了其精度的可靠性[7]。丁新原研究了塔里木沙漠公路防护林土壤水分特征曲线,得出VG模型对其模拟效果优于Gardner模型[8]。综上所述,水分特征曲线的研究多为农牧林中常见土壤,针对工程实际中常见砂土的研究相对较少。然而,土壤水分特征曲线在边坡的稳定性分析、砂土的湿热迁移研究方面同样具有广泛的应用需求。为此,本文拟对工程中常用的砾砂、粗砂、中砂、细砂、粉砂的水分特征曲线进行测试分析,以期得到经验公式,为工程实际服务。
1 材料与方法
1.1 实验材料
本次实验以山西忻州豆罗砂作为实验材料,经过筛分、配制得到砾砂、粗砂、细砂、中砂、粉砂5种砂土,砂土分类标准参照《土力学与地质基础》[9],5种砂土颗粒级配情况见表1,级配曲线见图1。

表1 砂土颗粒级配 %

图1 砂土颗粒级配曲线Fig.1 Sandy soil particle size distribution curves
1.2 实验方法
1.2.1 实验步骤
本次实验采用张力计法进行测试。单次称取1 kg已烘干砂土,按设计工况加入定量水,拌制均匀装入圆柱形桶中(Ф=110 mm,h=1 200 mm),用击实锤定量击实,然后在土体表面覆盖塑料保鲜膜密封,最后将张力计陶土头一端刺穿保鲜膜插入土体,待24 h后张力计读数达到稳定后,进行读数与记录。
1.2.2 注意事项
(1)砂土拌制、装填、击实、覆膜的整体时间要控制在3 min以内,以减少水分蒸发。
(2)每组实验进行3次重复测量,最后取平均值作为该组实验的基质吸力测试值。
2 结果与分析
2.1 基质吸力与质量含水率的关系
对实验数据进行处理,可得到基质吸力与质量含水率的关系曲线,即水分特征曲线见图2。从图2中可以看出:5种砂土的基质吸力均随含水率增加而减小;粗砂水分特征曲线在曲线两端趋近于砾砂,细砂水分特征曲线在曲线两端趋近于中砂;细砂水分特征曲线呈“反S”形,在含水率为4%时出现第1拐点A,在含水率为6%时出现第2拐点B,A点之后随含水率增加基质吸力呈现急剧减小的趋势,B点之后随含水率增加基质吸力大小逐渐趋于稳定;砾砂、粗砂、中砂、粉砂水分特征曲线呈“L”形,分别在含水率为2.5%、3.5%、5.0%、14.0%出现水分曲线变化的拐点C,C拐点之后随含水率增加基质吸力大小逐渐趋于稳定;同等含水率条件下,基质吸力大小顺序为粉砂>细砂>中砂>粗砂>砾砂。

图2 基质吸力与质量含水率关系曲线Fig.2 Relationships between matrix suction and mass water content
2.2 基质吸力与饱和度的关系
根据饱和度计算公式Sr=Vw/Vv=ωρd/(nρw)可求得5种砂土不同含水率下的砂土饱和度,然后建立基质吸力与饱和度的关系曲线,见图3。土壤饱和度是被水充满的孔隙体积与孔隙总体积之比,在干密度不变的条件下,其随含水率增加而增加,因此基质吸力与饱和度的关系曲线与水分特征曲线相似。从图3中可以看出:细砂在饱和度为13.72%时出现第1拐点,在饱和度为20.58%时出现第2拐点;砾砂、粗砂、中砂、粉砂分别在10.53%、12.49%、16.81%、48.22%出现拐点。

图3 基质吸力与饱和度关系曲线Fig.3 Relationships between matrix suction and saturation degree
2.3 基质吸力与孔隙率、细粒组含量的关系
通常认为孔隙率与细颗粒含量是影响土壤基质吸力变化的主要物理性质指标。此处采用烘干法测得5种砂土的孔隙率,采用筛分法测得其细粒组(d≤0.075 mm)含量见表2。从表2中可以看出孔隙率大小顺序为中砂>细砂>粉砂>砾砂>粗砂,细粒组含量大小顺序为:粉砂>细砂>粗砂>中砂>砾砂,显然以上顺序与同等含水率下砂土基质吸力大小排列顺序均不一致,表明仅依据孔隙率、细粒组含量不足以断定不同砂土间基质吸力的大小关系。

表2 砂土物理性质指标 %
2.4 水分特征曲线拟合方程
2.4.1 三次多项式拟合结果
在Excel中采用三次多项式对水分特征曲线进行方程拟合,其方程式为:
s=Aω3+Bω2+Cω+D
式中:s为土壤基质吸力;ω为质量含水率;A,B,C,D为拟合参数。
拟合结果见表3,拟合曲线见图4。各曲线R2值均大于0.98,实测值分布与拟合曲线较为吻合,表明该拟合方程拟合度较高。

表3 三次多项式参数拟合结果Tab.3 Fitting results of three polynomial parameters
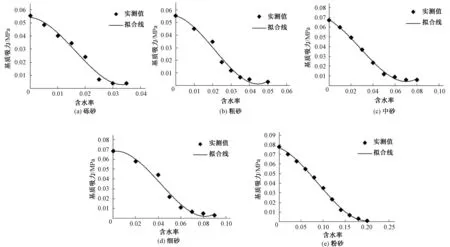
图4 三次多项式拟合曲线Fig.4 Three polynomial fitting curves
2.4.2 Van Genuchten模型拟合结果
常用的土壤水分特征曲线模型有Tyler-Wheatcraft分形方法、Brooks和Corey方程、Gardner模型、Van Genuchten模型等[10-13],其中以Van Genuchten模型应用最为广泛,其方程表达式为:
式中:θ为土壤含水率;θr为滞留含水率;θs为饱和含水率;h为土壤吸力,cm或Pa;α,m,n为参数,m=1-1/n。
杨改强在文献[14]中详细介绍了利用MATLAB率定Van Genuchten模型参数的方法。此处即采用该方法对5种砂土的Van Genuchten模型参数进行率定,率定结果见表4,拟合曲线见图5。砾砂、粗砂、中砂、的实测点分布与拟合曲线偏差较大;细砂、粉砂偏差较小,拟合度相对较高。

表4 Van Genuchten模型参数率定结果Tab.4 Setting results of Van Genuchten model parameters

图5 Van Genuchten拟合曲线Fig.5 Van Genuchten fitting curves
2.4.3 2种拟合结果比较分析
相关系数R2与相对误差PBIAS是常用的模型优劣的评价指标,其计算公式分别为:
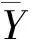
相关系数R2用于表示模拟值与实测值的拟合效果,值越大拟合效果越好;相对误差PBIAS用于表示模拟值与实测值之间的差距,正值时表示模拟值偏小,负值相反,其绝对值越小,拟合效果越好[15]。根据以上公式计算可得2种拟合结果的R2值与PBIAS值见表5。从表5中可以看出5种砂土所对应的三次多项式R2值均大于Van Genuchten对应值,当砂土种类为粉砂时,2种方法的R2值接近且均大于0.99;细砂所对应的三次多项式PBIAS绝对值略大于Van Genuchten模型对应值,除此之外,其他砂土三次多项式PBIAS值均小于Van Genuchten模型对应值。从5种砂土整体拟合效果看,三次多项式优于Van Genuchten模型。

表5 R2值与PBIAS值Tab.5 R2 values and PBIAS values
3 结 论
(1)细砂的水分特征曲线呈现“反S”形曲线,砾砂、粗砂、中砂、粉砂呈现“L”形曲线。砾砂、粗砂、细砂、中砂、粉砂分别在质量含水率大于2.5%、3.5%、5.0%、6.0%、14.0%,饱和度大于10.53%、12.49%、16.81%、20.58%、48.22%后,基质吸力大小趋于稳定。
(2)同等含水率条件下,5种砂土基质吸力大小为粉砂>中砂>细砂>粗砂>砾砂,该顺序与孔隙率大小排列顺序以及细粒组含量多少排列顺序均不一致,表明仅依靠孔隙率、细粒组含量无法判定不同砂土间基质吸力的大小关系。
(3)通过对比分析2种拟合方程的拟合效果,得出三次多项式对5种砂土水分特征曲线的拟合效果优于Van Genuchten模型,可以当作经验公式进行实际应用,且该拟合方程拟合过程简单快捷、易于理解,便于现场测试人员快速掌握和使用。
[1] 刘荣豪,裴亮. 土壤水基质吸力研究进展[J]. 节水灌溉,2013,(5):34-36.
[2] 雷志栋,杨思秀,谢森传. 土壤水动力学[M]. 北京:清华大学出版社,1988:15.
[3] 刘小文,常立君,胡小荣. 非饱和红土基质吸力与含水率及密度关系试验研究[J]. 岩土力学,2009,(11):3 302-3 306.
[4] 付丛生,陈建耀,曾松青,等. 珠三角滨海小流域土壤水分吸力及特征曲线研究[J]. 中国生态农业学报,2010,(3):507-513.
[5] 孙 迪,夏静芳,关德新,等. 长白山阔叶红松林不同深度土壤水分特征曲线[J]. 应用生态学报,2010,(6):1 405-1 409.
[6] 郑荣伟,冯绍元,郑艳侠. 北京通州区典型农田土壤水分特征曲线测定及影响因素分析[J]. 灌溉排水学报,2011,(3):77-81.
[7] 姚姣转,刘廷玺,王天帅,等. 科尔沁沙地土壤水分特征曲线传递函数的构建与评估[J]. 农业工程学报,2014,20:98-108.
[8] 丁新原,周智彬,雷加强,等. 塔里木沙漠公路防护林土壤水分特征曲线模型分析与比较[J]. 干旱区地理,2015,(5):985-993.
[9] 孔 军,高 翔.土力学与地质基础[M]. 2版. 北京:中国电力出版社,2008:33.
[10] Tyler S W, S W Wheatcraft . Application of fractal mathematics to soil water retention estimation [J] . Soil Science Society of America Journal, 1989,53:987-996.
[11] 李春友,任 理,李保国. 利用优化方法求算Van Genuchten方程参数[J].水科学进展,2001,12(4):473-478.
[12] Huang G H , Zhang R D , Huang Q Z . Modeling soil water retentioncurve with a fractal method[J].Pedosphere,2006,16(2):3-12.
[13] Van Genuchten R. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils [J] Soils Scisoc Am J,1980,44(5):829-898
[14] 杨改强,霍丽娟,杨国义,等. 利用MATLAB拟合Van Genuchten方程参数的研究[J]. 土壤,2010,(2):268-274.
[15] 刘贵花,栾兆擎,阎百兴,等. 基于SWAT模型的三江平原沼泽性河流的径流模拟[J]. 水文,2014,(1):46-51.
