冻融土壤Philip入渗模型参数的BP预报模型

2017-03-21李昊哲樊贵盛

节水灌溉 2017年5期

李昊哲，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

冻结土壤指的是温度在0 ℃或0 ℃以下，并含有冰的各种岩土和土壤，一般分为短时冻土、季节性冻土以及多年冻土。其中季节性冻土指的是持续半年至数月的冻土，而我国有超过54%[1]的土地位于季节性冻土区。据调查，我国北方大部分地区的冬、春灌溉都是在冻融条件下进行，为了确定合理的灌水技术参数和科学利用水资源，研究在冻融条件下水分的入渗特性便显得必要。同时，冻融条件下水分的入渗特性的研究对综合评价地表、地下水资源，高效利用土壤水资源具有有重要的意义。

多年来，学者们对于非冻融土壤的入渗过程、特性和模型进行了大量的研究，相对而言对冻融土壤入渗的研究较少。冻融土壤入渗是指具有一定温度的灌溉水垂直向下进入冻融土壤的过程[2]。上世纪90年代以来，人们对冻融土壤的研究也在逐步深入，樊贵盛，郑秀清[3]通过冬季大田耕作土壤的系列跟踪试验，分析了冻融土壤的减渗机理和地下水埋深对冻融土壤水分入渗特性影响，得出冻融土壤的入渗能力随地下水埋深的增加而增加的研究结论。Thunholm[4]等人对冻结黏土的土壤水分入渗特性进行了研究分析。郑秀清，陈军锋，邢述彦[5]针对不同的地表覆盖对冻融土壤入渗能力及入渗参数进行了研究，结果表明冻融土壤入渗能力主要受冻层的控制。彭振阳、黄介生[6]等研究了季节性冻融土壤水分运动规律，从定性和定量两个方面分析了潜水浅埋深条件下季节性冻融土壤水分运动的一般规律，表明冻结期内土壤水分向上运动，潜水补给土壤水，消融期则以20～40cm深度为界，土壤水分向上下两端运动。

土壤传输函数法是指利用易获得的土壤基本理化参数，如土壤含水率、土壤容重、土壤有机质等，预测土壤其他物理参数的方法。黄元仿[7]成功利用土壤理化参数估算了不同含水率或基质势下的土壤导水率。王志强[8]通过土壤基本物化参数，准确估算饱和含水率、田间持水率等水力特征参数。也有人在土壤水分入渗参数预测方面应用了土壤传输函数，如武雯昱[9]进行了非冻融条件下土壤水分入渗Kostiakov模型参数的BP预报模型研究。Philip[10]入渗模型属于半经验半理论模型，其入渗公式形式简单，各参数的物理意义明确，被广泛应用于土壤入渗的研究和土壤一维垂直入渗过程的表述。而人们对于冻融土壤条件下，Philip入渗模型参数的预测还未曾有相关报道。本文基于BP神经网络的方法，对季节性冻融土壤水分入渗Philip模型参数进行预测，实现以冻融土壤基本理化参数为输入变量，Philip入渗模型参数为输出变量的土壤传输函数研究，为春、冬季冻融土壤的灌溉提供依据，以达到冬季储水灌溉节约用水，提高水资源利用率的目的。

1 试验材料与方法

1.1 试验条件

本文所涉及的土壤水分大田入渗试验在中国北方地区的山西省汾河灌区进行。试验区处于汾河灌区最下游，属大陆性半干旱季风气候区，年平均气温10.43 ℃，最高气温39.5 ℃，最低气温-28.2 ℃；年际降雨量453 mm，年际变化大；试验区土壤从11月到次年3月属于冻融土壤，1月份最冷，3月份开始解冻，最大冻土深度达95 cm。

试验区属冲积平原地貌，地形平缓。土壤母质为汾河冲洪沉积物，土壤类型为浅色草甸土，地下水埋深在1.0～3.5 m，耕层深度为15～22 cm，耕作层土壤密度为1.00～1.46 g/cm3，犁底层土壤密度为1.383 g/cm3，土壤有机质含量为1.15%左右，耕作层黏粒含量13%左右，粉粒含量65%左右，属粉沙质壤土。

1.2 试验仪器与方法

本次大田入渗试验主要利用双套环入渗仪进行，其中外环直径60.0 cm，内环直径26.0 cm，内外环高度均为25cm。由于冻结土壤比较严实，在冬季无法将入渗环打入土壤中。为解决这一问题，试验中加工了百余套双套环入渗内环，并将其在地表封冻前一次性预埋在试验地块，下环深度20 cm到达犁底层。入渗水量采取人工分时段量筒计量加水，非冻融期的土壤水分达到稳渗状态的时间一般在60 min左右，但由于冻融期土壤入渗速率较慢，入渗达到稳定的时间将比非冻融期长，为保证入渗过程的完整性，确保试验成功，本试验水分稳定入渗的时间取90 min。试验中整个入渗过程用水均采用水井清水，水温在4～9 ℃。

土壤的常规理化性质参数包括土壤含水率、土壤干密度、土壤质地、土壤有机质含量、气温以及分层地温等。土壤含水率测定用传统烘干称重法测量获得；土壤干密度通过腊封法进行测定得到；土壤质地通过筛分+比重计法得到筛分曲线，然后分析土壤的颗粒级配，进而确定土壤质地；试验点土壤有机质含量的测定是利用化学的方法通过重铬酸钾容量法来测定；气温采用试验站气象设施观察得到，分层地温采用预埋的热敏电阻获得。

1.3 建模样本

根据大田冻融土壤的系列入渗试验得到累积入渗量I与入渗历时t的对应关系，由Philip入渗公式I=St0.5+At，拟合出参数S和A。根据系列试验组数拟合得到130组累积入渗量I、Philip入渗模型参数S和A，见表1。

表1 冻融土壤Philip入渗模型中的参数值

与上述120组累积入渗量I、入渗模型参数S和A相对应的土壤基本理化参数见表2。

表2 冻融土壤理化参数

由表1和表2的入渗模型参数和土壤基本理化参数共同构成建模数据样本。在120组样本中，选取113组作为建模训练样本，7组作为所建预测模型的检验样本。

1.4 BP神经网络方法

人工神经网络简称神经网络，是一种模拟生物神经网络，对各类信息进行处理的数学运算模型。人工神经网络以其特有的对非线性信息的处理能力，使得它在各个领域都解决了很多实际问题。而在众多人工神经网络模型中，BP神经网络因为其具有结构简单、可操作性强、有较强的自学习能力等优点，是目前研究最为成熟、应用最为广泛的人工神经网络模型。

BP神经网络是具有输入层、隐含层和输出层的3层神经网络，其结构示意见图1。

图1 BP神经网络结构

隐含层的个数可以为多个，本文选取只含有1个隐含层的3层BP神经网络。

本文借助于计算机编程语言，利用matlab 7.0实现BP神经网络模型的建立，利用神经网络工具箱中的newff函数进行建模，同时选取trainlm算法对所选取的数据样本进行分析处理。

由于BP神经网络神经元的响应函数为Sigmoid函数，要求输出输入变量的值为(-1，1)，这就要求在将样本数据导入到神经网络模型之前，需要对数据样本进行归一化处理，本文选取如下公式进行：

(1)

同时，根据数据样本的特点，本文隐含层的激活函数选tansig函数，输出层的激活函数选择purelin函数。BP神经网络训练的学习率一般取值为0.01～0.80；BP神经网络训练的最大学习迭代次数一般取值为1 500～3 000；BP神经网络训练要求精度一般取值为0.001～0.000 01。

2 输入、预测变量的确定

2.1 预测变量

本文基于大田耕作冻融土壤水分入渗资料，借助于BP神经网络的方法，就Philip入渗模型参数进行预测。Philip入渗模型如下：

I=St0.5+At

(2)

式中：I为累积入渗量，cm，与入渗时间有关；A为土壤的相对稳定入渗率，接近土壤的饱和水力传导度，cm/min；S为吸渗率，在数值上等于第1个单位时段末的累积入渗量减去稳渗率A后的值，cm/min0.5；t为入渗时间min。

利用BP神经网络预测模型进行预报时，吸渗率S和稳渗率A为预测参数，即为本文BP神经网络预测模型的输出参数。

2.2 预测模型的输入变量

2.2.1 预测变量吸渗率S的输入变量

据有关学者的研究影响吸渗率S的因素有土壤含水率、耕作层土壤质地、土壤密度、土壤温度、当地气温以及灌溉用水的水温等[10]。

为保证预测的精度，在选取预测模型的输入参数时应选择对输出变量影响较大的因子。由于吸渗率S在数值上接近于第1个单位时段末(1 min)的累积入渗量，且冻土入渗时，入渗速度小，湿润锋推进缓慢，故S应只与地表表层的土壤理化指标有关，这里取0～10 cm的土壤理化指标作为输入变量。

在土壤结构和质地条件相同的情况下，表层土壤含水率决定着第1个时段末的累积入渗量，即影响着S的取值。对于冻结土壤来说，含水率越大，则说明土壤中积冰量越大，将导致土壤连通性较差，第1个单位时段末的累积入渗量越小。

土壤质地是土壤固相物质各粒级土粒的配合比例。它通过改变土粒的表面能、土壤孔隙度和分布来影响土壤水分运动和水力传导度，进而影响土壤水分入渗能力，一般用土壤中黏粒、粉粒及沙粒的百分含量来表征土壤质地。其中黏粒含量越高，质地越重，土壤颗粒的吸附能力就越强，孔隙越细小，导致同样时间内水分通量减小，土壤水分的入渗速度减小。

由于考虑的是冻结土壤，土壤温度作为结冰量的直接因素，对冻融土壤的水分入渗有着极大的影响。土壤温度越低，土壤中的含冰量就越高，直接导致土壤导水能力降低。且已有研究表明，地表下5 cm的土壤温度最能表征对土壤入渗的入渗影响。为保证数据的非负性，本次试验温度用开尔文温度表示，开尔文温度是以绝对零度作为计算起点的温度，常用符号T表示，单位为开尔文K，其中T=t+273.15(t是摄氏温度的符号)。

对于冻结土壤，灌溉水温越高，灌溉过程中越会融化土壤中的冰块，改变土壤冻结量，土壤冻结量变化会影响到土壤结构，从而影响到土壤水分的入渗。

所以最后确定土壤含水率θ1(0～10 cm)、耕作层(0～10 cm)黏粒含量w1、耕作层(0～10 cm)粉粒含量w2、耕作层(0～10 cm)土壤密度γ0、试验时土壤5 cm深度处温度T1以及灌溉用水的水温T2作为吸渗率S的预测输入参数，即吸渗率S的输入变量。

2.2.2 预测变量稳渗率A的输入变量

据有关学者的研究影响稳定入渗率A的因素有土壤含水率、耕作层土壤质地、土壤密度、土壤温度、当地气温以及灌溉用水的水温等[12]。

由于冻融土壤的入渗速率较慢，在90 min内入渗可以达到稳定状态，但此时的湿润锋应当在20 cm内，所以在选取预测模型的输入参数时，只取0～20 cm的土壤理化参数和温度作为输入参数。各变量的影响机理与吸渗率S相同。

冻结土壤中，随着土壤含水率的增高，土壤中的积冰量越多，导致其中的孔隙体积越小，持续影响着土壤入渗过程，对土壤的稳渗率也有较大影响。

土壤温度、土壤有机质、土壤质地、灌溉水温对稳渗率的影响与其对吸渗率的影响机理相同。

稳渗率A除受表层土壤的理化参数影响外，与犁底层的基本理化参数也有关系，本次试验选取0～10 cm土壤含水率θ1、10～20 cm土壤含水率θ2、耕作层(0～20 )黏粒含量w1、耕作层(0～20 )粉粒含量w2、0～10 cm土壤密度γ0、10～20 cm土壤密度γ1、试验时土壤5 cm深度处温度T1以及灌溉用水的水温T2作为稳渗率A的预测参数，即稳渗率A的输入变量。

3Philip入渗模型参数BP神经网络预报模型的建立

3.1 模型结构

采用Matlab 7.0建立BP模型结构如下：

net=

newff(minmax(traininput),[m,1],{'tansig','purelin'},'trainlm')

式中：newff为建立前馈神经网络的函数；traininput为模型的输入样本；minmax(traininput)为样本的范围；m指隐含层的神经元节点个数，本文在预测吸渗率S时，试算确定的节点数为1，预测稳渗率A时，试算确定的节点数为1； tansig为隐含层的激活函数；purelin为输出层的激活函数；trainlm为BP神经网络的反向传播训练函数。

将样本输入网络进行训练，神经网络学习训练经过迭代后收敛，并且网络完全准确地识别了学习样本，建立了输入参数与输出参数之间复杂的非线性映射关系。训练结果如下：

A=purelin[iw2×(tansigiw1×F+b1)]+b2

S=purelin[iw2×(tansigiw1×E+b1)]+b2

F=[θ1，θ2，w1，w2，γ0，γ1，T1，T2]

E=[θ1，w1，w2，γ0，T1，T2]

式中：iw2为模型隐含层到输出层的权值；iw1为模型输入层到隐含层的权值；b1为模型输入层到隐含层的阈值；b2为模型隐含层到输出层的阈值。

3.2 Phillip入渗模型参数的预测

基于对入渗公式参数实测数据的分析以及大量的试算工作最后确定各预测参数的训练参数。

对于吸渗率S， BP神经网络训练的学习率设定为0.01；BP神经网络训练的最大学习迭代次数设定为1 500；BP神经网络训练要求精度设定为0.000 1；隐含层节点数最后经过试算确定为25。最后当计算步数为257时，训练精度达到要求，训练结束。训练值见表3。

表3 吸渗率S的预测模型数值

对于稳渗率A，BP神经网络训练的学习率设定为0.01；BP神经网络训练的最大学习迭代次数设定为1 500；BP神经网络训练要求精度设定为0.000 01；隐含层节点数最后经过试算确定为11。最后当计算步数为128时，训练精度达到要求，训练结束。训练值见表4。

根据BP网络模型对土壤水分入渗参数的预测得到稳渗率A和吸渗率S的预测值，与实测值进行比较，计算绝对误差与相对误差，结果见表5。

表4 稳渗率A的预测数值

表5 A、S误差分析

由表5可知，稳渗率A预测值与实测值的绝对误差平均值为0.001 0 cm/min，最大值为0.005 6 cm/min，最小值为0；相对误差的平均值为6.390%，最大值为16.008%，最小值为0.229%。吸渗率S预测值与实测值的绝对误差平均值为0.002 1 cm/min0.5，最大值为0.040 4 cm/min0.5，最小值为0；相对误差的平均值为0.723%，最大值为11.195%，最小值为0.001%。误差完全在可接受的范围之内。由此可见，基于Philip半经验半理论土壤水分模型建立的BP神经网络预测模型有较高的可信度。

3.3 90 min累积入渗量的综合误差分析

根据预测所得的2个土壤水分入渗参数A和S，并将其代入得到Phillip入渗公式的表达式，求出90 min累积入渗量I90的预测值，与113组样本实测值相比较，分析其绝对误差与相对误差见表6。

由表6可知，90 min累积入渗量的绝对误差平均值为0.097 4 cm，最大值为0.537 2 cm，最小值为0.001 6 cm；相对误差的平均值为2.165%，最大值为8.990%，最小值为0.022%，误差完全在可接受的范围之内，与A和S值的误差相当。由此表明所建立的BP神经网络预报模型具有较高的精度。

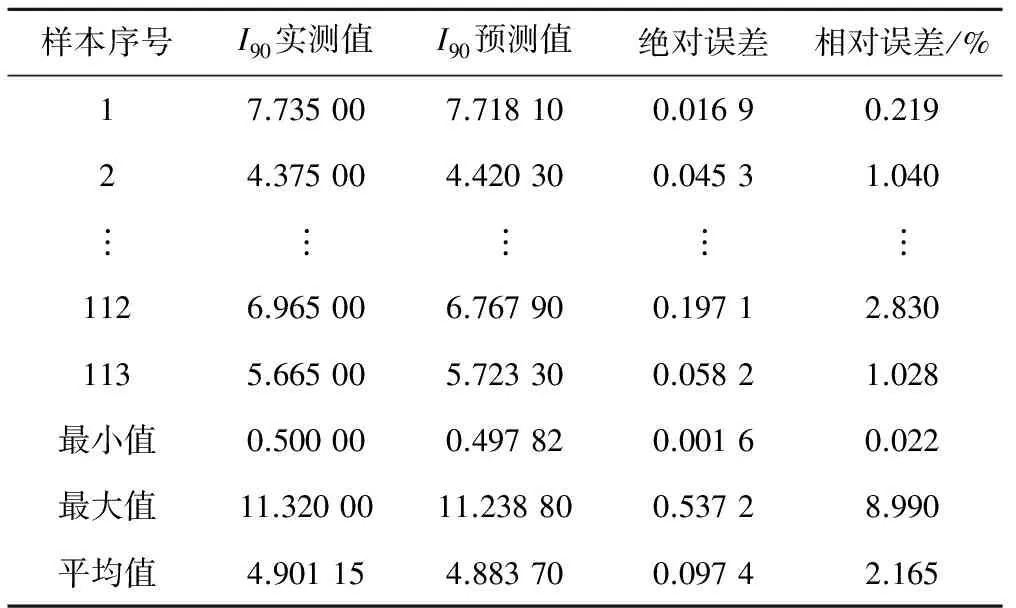
表6 I90误差分析 cm

3.4 模型检验

用试验预留的7组数据检验模型的预测精度，结果见表7。

由表7可知，对于吸渗率S的相对误差最大值为0.363%，最小值为0.004%，平均值为0.121%；稳渗率A的相对误差最大值为5.453%，最小值为0.229%，平均值为2.548%；90 min累积入渗量I90的相对误差最大值为2.914%，最小值为0.022%，平均相对误差为0.980%。实例检验结果表明Philip入渗模型的2个入渗参数的相对误差小，精度较高，应用所建立的BP预测模型能获得较好的效果。

表7 检验结果

4 结论

本文建立的基于BP神经网络模型的土壤水分入渗参数预测模型可以较好地反映Philip模型中入渗参数与多种影响因素之间的复杂的非线性关系，稳渗率A、吸渗率S和土壤水分累积入渗量I90综合影响的相对误差平均值分别为6.390%、0.723%和2.165%，相应的应用结果误差的平均值分别为2.548%、0.121%和0.980%，误差都在理想精度范围内，说明利用冻融土壤基本理化参数对入渗参数的预测是可行的，所建模型能较好预测出土壤水分入渗参数，可以为春、冬季冻融土壤的灌溉提供有力的技术支撑，同时，在一定程度上丰富了土壤传输函数的理论成果。

本文成功利用土壤传输函数法对冻融土壤的水分入渗参数作出预报，所选择的输入变量获得了满意的结果。经过反复试算，确定用土壤含水率、密度、质地、温度以及灌溉水温等参数对Philip土壤入渗模型参数S、A进行预测是可行的。

本文受试验验条件的限制，样本的数量和土壤的代表性不是十分的满意，在以后的研究中需在样本的扩大和土壤的代表定方面强化。

[1] 徐学祖,邓友生.冻土中水分迁移的实验研究[M].北京:科学出版社,1991.

[2] 樊贵盛,郑秀清.水分在季节性非饱和冻融土壤中的运动[M].北京:地质出版社,2002.

[3] 樊贵盛,郑秀清,贾宏骥.季节性冻融土壤的冻融特点和减渗特性的研究[J].土壤学报,2002,37(1):25-27.

[4] Thunholm B, L Lundin. Infiltration into frozen heavy clay soil[J].Nordic Hydrology,1989,20(3):153-166.

[5] 郑秀清,陈军锋,邢述彦.不同地表覆盖下冻融土壤入渗能力及入渗参数[J].农业工程学报,2009,25(11):22-28.

[6] 彭振阳,黄介生.季节性冻融土壤水分运动规律[J].武汉大学学报(工学版),2011,44(6):696-697.

[7] 黄元仿,李韵珠.土壤水力性质的估算----土壤转换函数[J].土壤学报,2002,39(4):517-522.

[8] 王志强,刘廷玺.寒冷干旱区土壤水力特性参数的模拟估算[J].沈阳农业大学学报,2004,35(5):426-428.

[9] 武雯昱,樊贵盛.基于Phillip入渗模型的土壤水分入渗参数BP预报模型[J].节水灌溉,2015,(10):25-29.

[10] Philip J R．The theory of infiltration about sorptivity and algebraic infiltration equations[J]. Soi. Sci., 1957,84(4)：257-264．