基于神经网络的温室土壤水分动态预测模型研究

万博雨，付 聪，郑世健，范玉德，刘知贵(.西南科技大学信息工程学院，四川 绵阳 6000；.中国物理研究院，化工材料研究所，四川 绵阳 6000)

土壤水分作为一种复杂的非线性耦合系统，易受外界环境因素的影响，且具有较强的时滞性[1]。对于温室小气候系统而言，虽然其隔绝了天气对土壤水分的直接影响，但地形、土壤空间变异性以及人类农业生产带来的影响依然存在。由于土壤空间变异性，传统施水方式在施水后无法降低土壤含水量空间分布差异，促使作物的长势不均。并且其未考虑土壤的时滞性，对土壤水分控制精度低。变量施水也叫变量灌溉或精准灌溉，其考虑到土壤空间变异性，通过对空间内实时精确施水，从而满足种植区所有作物的水分需求[2]。

若要实现温室精细化变量施水，首先需要实现对温室土壤水分的动态预测。目前，常用的土壤水分预测模型的方法主要有：土壤水量平衡模型[3]、土壤水动力学模型[4]、经验性模拟模型[5]和人工神经网络模型[6]等。上述方法在边界确定时可以获得较好结果，但在实际应用中经验性模拟模型的经验系数受时空分布的影响较大；土壤水量平衡模型需要测量和计算的因素较多，若缺少其中部分输入量，模型预测结果会产生较大误差；土壤水动力学模型中参数测量和计算较为复杂，妨碍模型的实际推广应用；人工神经网络模型一般以各层的历史土壤含水量(以一旬或一个月的平均值)作为输入，对未来某阶段土壤含水量变化情况进行预测，只能实现用水评估，而无法进行实时变量施水决策。现阶段对于土壤水分预测的研究主要集中于大田，鲜有对于温室的研究。而温室作为重要的农业设施，对温室土壤水分动态预测模型的研究，不仅有利于温室变量施水的实现，也对未来农业设施化的推广具有重要意义。

本文针对温室特点，分析了影响土壤水分动态预测模型精度的主要矛盾和传统预测模型存在的问题，模糊了土壤喷灌量，采用土壤内部水势变化反应土壤水流动态。参考土壤水势模型，将单位时间土壤含水量变化映射成土壤水势变化。在Delaunay三角剖分布点方法的基础上，将种植区域土体离散成若干单元，分别建立以表层测量点土壤含水量、土壤温度和单位时间土壤含水量变化量作为输入的BP神经网络模型和RBF神经网络模型预测未来时刻该单元中心土壤深层含水量，并利用温室中实测数据进行对比检验，得出RBF神经网络模型具有较好实用性，为温室精细化变量施水的实现奠定基础。

1 土壤水分动态预测模型问题描述

由于温室隔绝了外界气象因素对土壤水分的直接影响，并且可以通过补光、控湿、控温使种植区域土壤外部环境相对均一。假设土壤质地均一，则影响土壤水分动态预测模型精度的主要矛盾集中于水流在土壤内部渗透速度以及通过单一时刻数据对植物根系周围土壤水分所处状态和变化趋势的判定。喷灌施水状态下土壤各层含水量变化如图1所示。

图1 土壤含水量时间变化规律Fig.1 Variation of soil moisture content

实验表明土壤对施水、施肥等农业操作的响应具有强滞后性。通过采样得到的土壤墒情信息仅为当前时刻下的土壤含水量，无法判断此刻该片种植区域是否处于施水状态，导致一定延时之后土壤含水量预测的不确定性，土壤状态预测结果如图2所示。因此只以当前所采集的环境信息作为输入，通过神经网络进行预测会产生较大误差。

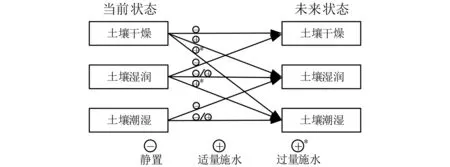
图2 土壤状态预测结果图Fig.2 Soil state prediction result

根据土壤水分运动方程，可构建温室中以喷灌垂直水分作用的二维土体模拟基本单元，定义该单元长度为UL，深度为UH，将整个土体模拟基本单元划分成m×n个单元格。垂直方向分为非饱和渗流区和地下水区，其中非饱和渗流区为整个土壤水动力学模型的核心。喷灌水文单元结构及其水文过程示意图如图3所示。

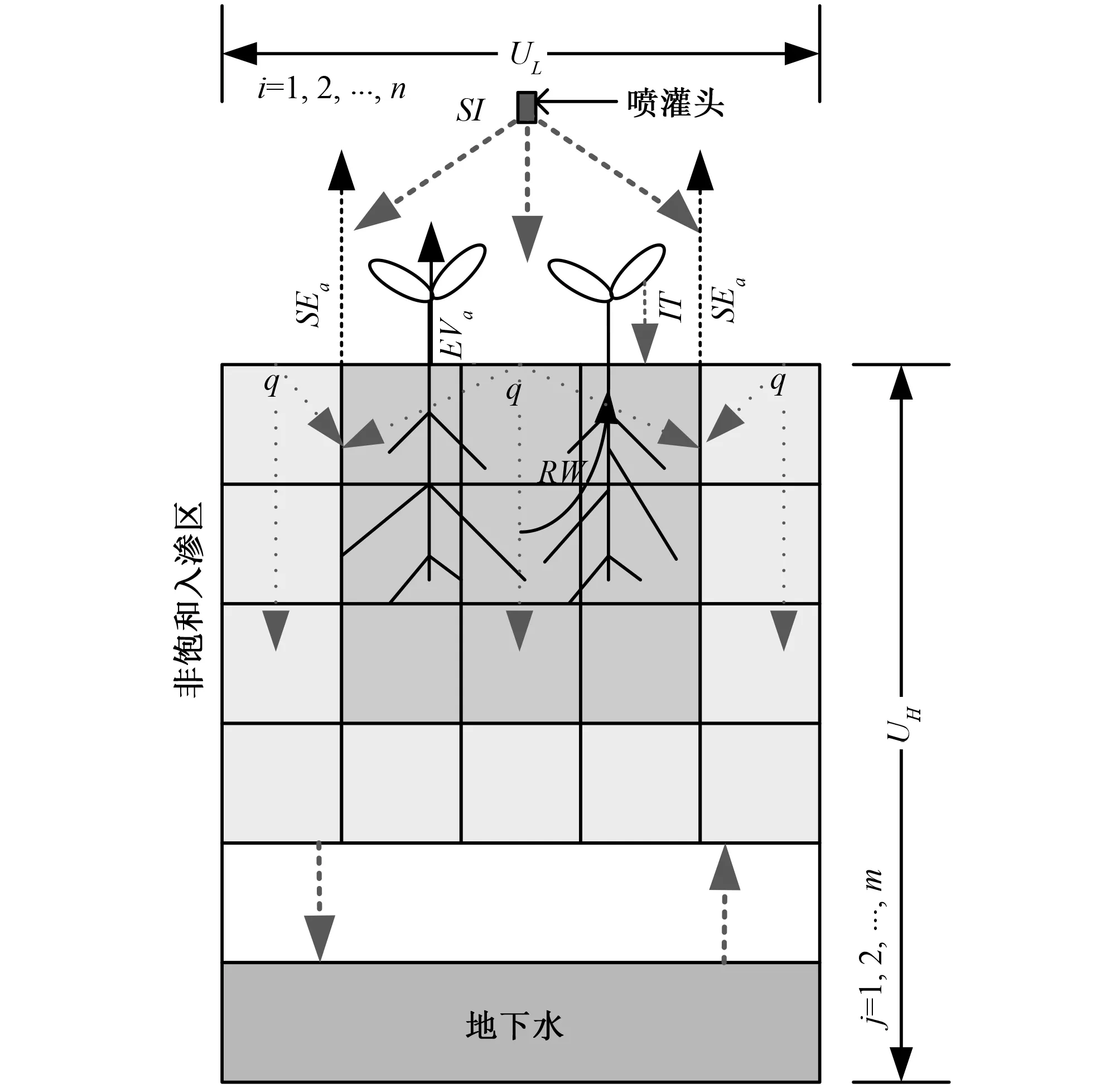
图3 喷灌水文单元结构及水文过程示意图Fig.3 Schematic diagram of hydrological unit structure and its water transform process

由图3可知，喷灌水是温室土壤水分补给的来源，喷灌水进入土壤向四周扩散，部分喷灌水因冠层截留IT可在作物附近直接形成下渗补给；水分消耗有植物蒸腾EVa、土壤蒸发SEa、根系吸水RW、深层下渗4种方式。可构建非饱和入渗区各单元内土壤水分动态数学模型，如公式(1)所示。

(1)

式中：i,j代表土壤单元；Vi为i单元土壤体积；SWi为i单元土壤体积含水率；SIi为总喷灌量在i单元入渗量；ITi为冠层截留量在i单元入渗量；SEa为单元表层土壤蒸发量；RWi为根系在i单元的吸水量；qij,out为i单元到相邻j单元的渗出量；qki,in为相邻k单元到i单元的渗入量。

但是该模型只适用于边界确定的情况，模型参数对整个模型的精确性起到决定性作用。并且模型参数(土壤水流、根系吸水量和植物蒸腾量等)测量困难、计算复杂，受地形和作物种植密度等因素影响较大。

2 神经网络动态预测模型的建立

BP(Back Propagation，反向传播)神经网络，由信息的正向传播和误差的反向传播两个过程构成。其作为一种以误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一，其结构如图4(a)所示。RBF(Radical Basis Function，径向基函数)神经网络，是一种3层前向网络。该网络使用径向基函数Φ(x)作为隐单元的“基”，组成隐层空间，即输入矢量可直接映射到隐空间，其结构如图4(b)所示,其中P为训练样本个数。

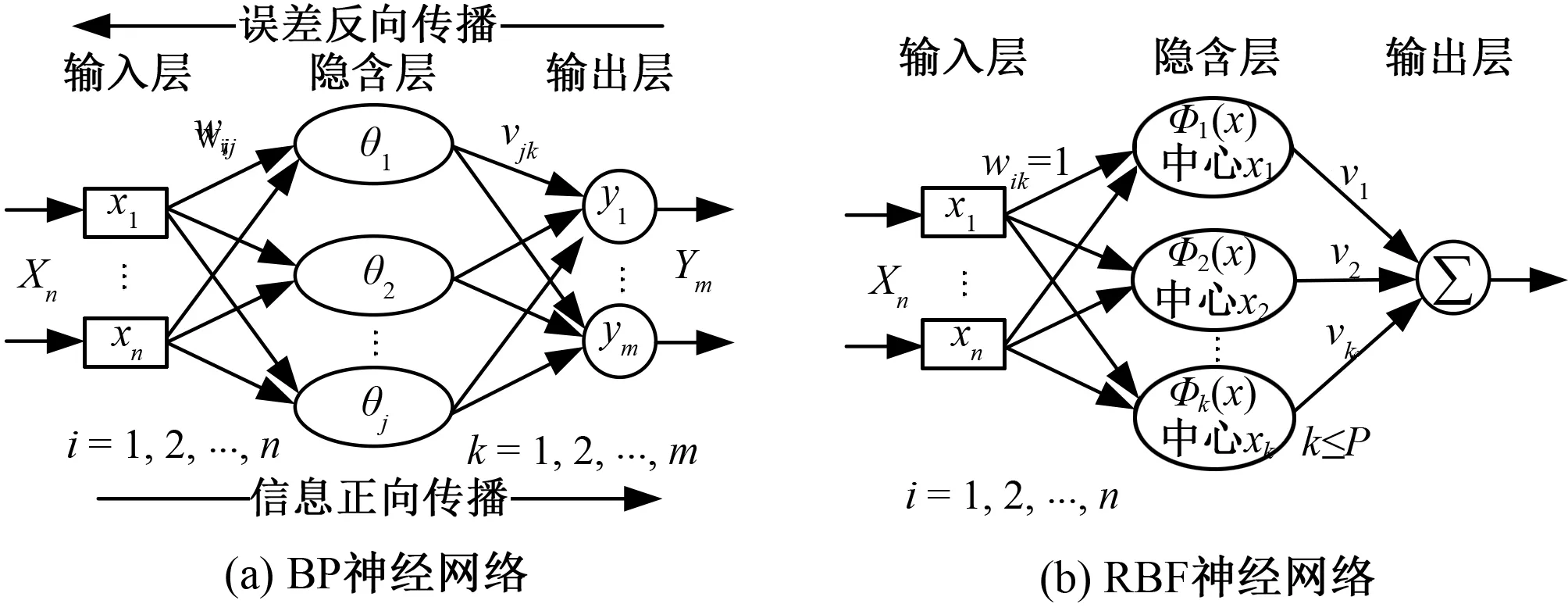
图4 神经网络结构图Fig.4 Neural network structure

2.1 模型输入、输出量的分析与确定

根据公式(1)可以发现影响土壤水分变化的主要因素为蒸发量、喷灌量和根系吸水量。针对温室种植区土壤蒸发量，通过控制温室中土壤外部环境因素(光照、空气温度、空气湿度等)，直接影响土壤蒸发量的因素仅为表层土壤温、湿度，故表层土壤温、湿度可作为神经网络的输入变量。

喷灌水通过入渗会形成土壤水流，土壤水流的大小不光反应出当前土壤所处状态，也受土壤蒸发、根系吸水、地形等综合作用影响。为了降低因喷灌施水设施硬件参数误差和在使用中发生异常或损坏带来的干扰，可以模糊喷灌量，利用土壤内部水流动态反应土壤水分情况。但是土壤水流的大小与运动状态无法通过传感器直接采集测量。

水在土壤-植物-大气连续体中的流动是由水势梯度驱动的，在水势差最大的地方水流最大[7]。当水流平衡的土壤系统受到外部过程影响(如蒸发、蒸腾或施水等)时，土壤水势的分布会发生变动[8]。土壤水势Ψ的表达式如下[9]：

Ψ=Ψg+Ψm+Ψs+Ψp+ΨT

(2)

式中：Ψg为重力势；Ψm为基质势；Ψs为溶质势；Ψp为压力势；ΨT为温度势。

重力势由土壤水海拔高度决定，可反应温室地形；基质势是土壤吸附力作用的结果，不仅影响土壤水分的吸持，而且影响土壤水的运动；植物吸水主要由于溶质势作用，受土壤水中溶质影响；压力势和温度势主要受压力和温度作用。对于非饱和土壤，压力势和温度势通常忽略不计，在土层深度一定时，主要影响土壤水势大小的为基质势和溶质势[10]。

2017年，江苏大学吴沿友等人[11]依据吉布斯自由能公式推导出土壤水势模型：

(1+P)ΨX=Ψ0+kln(1+P)

(3)

式中：P为待测土壤含水量；ΨX为待测土壤水势；Ψ0和k为模型参数。

由于土壤含水量不能为负，所以该模型可转化为：

(4)

结合公式(2)、(4)，可将复杂的土壤水势抽象成关于土壤含水量的函数，即：

Ψ=f(1+P)

(5)

所以将土壤水势的变化趋势映射成该点单位时间内土壤含水量的变化程度(土壤含水量和时间函数的斜率)作为神经网络的输入变量，可以反映出土壤水流的运动趋势，有助于对温室土壤所处状态进行判断并提高预测精度。

同一位置垂直向上不同深度的土壤水分数据具有显著的差异[12]。由于灌溉量等因素的影响，表层土壤含水率变化较大，土壤20 cm以下土壤含水率较土壤表层相对稳定，且同一深度土壤的物理性质在整个作物生长周期内较为稳定[13]。

综上所述，以预测区域内各测量点土壤表层0～10 cm的土壤温、湿度和单位时间下土壤含水量变化量作为模型的输入变量。同时，考虑土壤响应的滞后性，选择预测区域中心30 min后土壤25 cm处含水量作为模型的输出变量。

2.2 模型输入、输出层神经元数的确定

为使土壤水分动态预测模型能够实现变量施水，则需将整个温室种植区细化成多个区域，分别对每个区域进行单独预测。为提高模型预测精度，即需要感知的环境信息具有代表性和准确性。故以网格化Delaunay三角剖分布点方法为基础，传感器布设位置如图5所示。

图5 传感器布设位置Fig.5 Sensor deployment location

若将预测基本单元限定为1 m2的网格，根据图4可知模型的输入为4个传感器采集所采集的土壤温、湿度和其单位时间内土壤含水量变化程度，即输入层为12个神经元。由于以预测区域中心25 cm处含水量作为输出变量，即输出层为1个神经元。

2.3 BP网络及RBF网络预测模型的生成

根据上述输入、输出量和输入、输出层神经元个数，利用MATLAB神经网络工具箱，分别建立BP神经网络模型和RBF神经网络模型。

BP神经网络生成步骤：

(1)利用mapminmax函数对输入、输出样本进行归一化处理，将样本数据转化成[0,1]区间的数据，防止网络计算时发生计算溢出。

(2)根据经验公式、网络训练情况和精度要求，确定隐层个数N。经验公式如式(6)所示：

(6)

式中：Ni，No分别为输入、输出神经元个数；A为1～10之间的常数。

(3)利用newff函数创建BP网络，设置最大训练次数、训练目标最小误差、学习速率等参数。

(4)利用sim函数将测试集带入训练好的网络进行测试，并将测试结果反归一化。

RBF神经网络生成步骤：

(1)利用mapminmax函数对输入、输出样本进行归一化处理。

(2)根据输入样本数量，选用newrb或newrbe函数创建RBF网络，设置目标误差、径向基函数密度等参数。

(3)利用sim函数将测试集带入训练好的网络进行测试，并将测试结果反归一化。

3 温室土壤水分动态预测模型验证与比较

模型以西南科技大学生命科学与工程学院费约果种植基地中费约果扦插育苗大棚作为验证对象。选取其中4 m2方形种植区域，利用Delaunay三角剖分布点方法布置MS10型传感器(感测范围为直径7 cm、高10 cm的圆柱)，检测土壤温、湿度，并以1 min作为时间节点，计算土壤含水量变化程度。将方形种植区网格化分成4个1 m2基本单元，在每个基本单元中心，距离土壤表面25 cm处水平放置一个MS10型传感器，检测30 min后土壤含水量。模拟温室施水对该区域进行多次周期性静置和喷灌施水，记录数据样本。

依照模型建立方法，建立最终网络结构为(12，7，1)的BP神经网络模型和径向基函数密度为1的RBF神经网络模型。以40个样本作为训练集，5个样本作为测试集与预测结果对比，模型训练结果对比如图6所示，模型预测结果对比如图7所示。

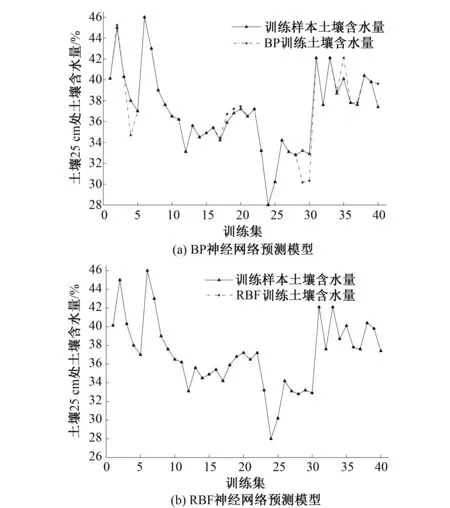
图6 模型训练结果对比图Fig.6 Comparison of model training results

图7 模型预测结果对比图Fig.7 Comparison of model prediction results

根据图6和图7可以看出以Delaunay三角剖分布点方法为基础，以土壤温、湿度和单位时间土壤湿度变化量作为输入的BP神经网络模型和RBF神经网络模型均能有效预测出土壤水分发展趋势和深层土壤含水量。模型预测结果误差评估对比如表1所示。

表1 模型预测结果误差评估对比 %

通过比较，当训练样本容量为40时，RBF神经网络的预测精度要高于BP神经网络。为了研究不同训练样本个数下两种神经网络模型预测精度，分别以20、40、80个数据样本进行训练，所得预测结果精度如表2所示。

在不同训练样本数量下，两种模型预测精度均适用于实际应用，其中RBF神经网络预测模型精度均优于BP神经网络预测模型，并且随着训练样本数量的增加，RBF模型预测精度不断增加并趋于稳定，BP神经网络开始出现过拟合现象。

表2 不同训练集个数模型预测结果对比Tab.2 Comparison of prediction result of different training set number models

4 结 语

本文利用网格化Delaunay三角剖分布点方法在种植区域布设土壤墒情传感器，将种植区域离散成若干面积为1 m2的单元。以每个单元传感器采集的表层0～10 cm土壤温度、土壤含水量和单位时间土壤含水量变化量作为输入量，以30 min后该单元土壤25 cm处含水量作为输出，使用MATLAB分别建立BP神经网络模型和RBF神经网络模型。实验表明样本个数分别为20、40和80时，两种预测模型均能有效预测出土壤水分发展趋势和深层土壤含水量。证明以土壤含水量、土壤温度和单位时间土壤含水量变化量作为输入的神经网络预测模型能够应用于变量施水作业中。由于RBF神经网络预测模型的预测精度高于BP神经网络预测模型，并且BP神经网络易发生局部最优，训练花费时间较长，故RBF神经网络预测模型为优选。

虽然该预测模型能够为温室变量施水提供决策条件，但其核心是预测种植区各个离散单元土壤水分，对于未来连栋式大规模温室可能会对核心计算单元带来较大压力，未来将在计算运行调度算法上进行研究，实现大面积温室精细化变量施水作业。

[1] 陈昌华, 谭 俊, 尹健康, 等. 基于PCA-RBF神经网络的烟田土壤水分预测[J]. 农业工程学报, 2010,(8):85-90.

[2] 赵伟霞, 李久生, 杨汝苗, 等. 田间试验评估圆形喷灌机变量灌溉系统水量分布特性[J]. 农业工程学报, 2014,(22):53-62.

[3] 王季槐, 赵松岭, 叶振欧. 定西半干旱地区春小麦农田土壤水分动态的计算机模拟[J]. 土壤学报, 1987,(4):388-391.

[4] 孙 林, 罗 毅. 膜下滴灌棉田土壤水盐运移简化模型[J]. 农业工程学报, 2012,(24):105-114.

[5] 尚松浩, 雷志栋, 杨诗秀. 冬小麦田间墒情预报的经验模型[J]. 农业工程学报, 2000,(5):31-33.

[6] 侯晓丽, 冯跃华, 吴光辉, 等. 基于人工神经网络土壤墒情动态预测模型应用研究[J]. 节水灌溉, 2016,(7):70-72.

[7] Sellin A. The dependence of water potential in shoots of Picea abies on air and soil water status[J]. Annales Geophysicae,1998,16(82):470-476.

[8] V Couvreur, J Vanderborght,L Beff,et al. Horizontal soil water potential heterogeneity: simplifying approaches for crop water dynamics models[J]. Hydrology and Earth System Sciences,2014,18(5):1 723-1 738.

[9] Marco Bittelli. Measuring soil water potential for water management in agriculture: a review[J]. Sustainability,2010,2(5):1 220-1 226.

[10] 窦超银, 吕国华. 土壤水势控制在农业灌溉应用中的研究进展[J]. 节水灌溉, 2013,(2):56-59.

[11] 吴沿友, 胡林生, 谷睿智, 等. 两种土壤含水量与水势关系[J]. 排灌机械工程学报, 2017,(4):351-356.

[12] 孙 凯, 王一鸣, 杨绍辉, 等. 区域墒情特征的研究[J]. 水利学报, 2005,(3):355-359.

[13] 冀荣华, 李 鑫, 张舒蕾, 等. 基于时延神经网络的多深度土壤含水率预测[J]. 农业工程学报, 2017,(S1):132-136.