投影寻踪模型在水稻灌溉制度评价中的应用

李欣欣，张宏立

(新疆大学电气工程学院，乌鲁木齐 830047)

目前中国有大约60%人口的口粮以大米为主，水稻是我国最主要的粮食作物，但传统的淹水栽培每亩耗水量可达400～600 m3，而中国是水资源短缺且水旱灾害频繁发生的国家，因此优化水稻灌溉制度成为解决粮食安全与水资源短缺两大紧迫问题的关键突破口。

水稻灌溉涉及因素众多且具有模糊性难以定量化，如光照强度、土壤、水、肥料以及大气等，因此水稻在不同生育阶段所表现出的生理和形态特征则是众多因素作用的综合结果[1]，故水稻灌溉制度评价是一个具有不确定性的高维数据综合评价问题。对于该类问题的处理方法主要有模糊综合评判法[2, 3]、主观赋权法[4]、灰色系统评价法[5]和基于熵的综合评价方法[6, 7]等。目前广泛应用的是模糊综合评判法，如朱庭芸等采用了模糊数学理论与田间试验相结合的方法，提出了水稻的优化灌溉模式[1]，但该方法在权重矩阵赋值时存在一定的主观任意性，影响最终的评价结果。

基于上述原因，提出了基于粒子群优化投影寻踪模型的水稻灌溉制度评价方法。投影寻踪模型是20世纪70年代出现的一种新兴统计方法[8]，该方法通过最大化数据特征确定最佳投影方向，以此判断各评价指标对综合评价目标的贡献度，并通过最佳投影方向与评价指标的线型投影得到投影值，根据投影值的大小可进行水稻灌溉制度的综合评价。该方法不存在专家赋权的人为干扰，克服了传统处理方法的缺点，增强综合评价结果的准确性。

本文选取水稻分蘖及灌浆2个重要生育阶段，分别建立模型并对4种灌溉模式进行综合评价，将评判结果与实际数据进行对比分析，以验证该方法的准确性与可行性。

1 基于粒子群算法的投影寻踪模型

投影寻踪[9]是用来分析和处理高维观测数据，尤其是非线性、非正态高维数据的一种新兴统计方法。它通过把高维数据投影到低维空间，寻找能反映原高维数据结构或特征的投影，达到研究分析高维数据的目的。

在实际应用中，投影寻踪模型最佳投影方向的确定是一个关键，为克服传统优化方法只对特定目标函数有效的局限性，本文采用粒子群算法[10]优化投影方向，建立基于粒子群算法的投影寻踪模型。

基于粒子群算法的投影寻踪模型建模过程如下。

(1)样本评价指标集的归一化处理。设各指标值的样本集为{x*(i,j)|i=1,2,…,n;j=1,2,…,p}，其中x*(i,j)为第i个样本第j个指标值；n，p分别为样本的个数和指标的数目。为消除各指标值的量纲和统一各指标值的变化范围，可采用下式进行极值归一化处理。

对于越大越优指标(正向指标)：

(1)

对于越小越优指标(逆向指标)：

(2)

式中：xmax(j)，xmin(j)分别为第j个指标值的最大值和最小值；x(i,j)为指标特征值归一化的序列。

在对样本评价指标集归一化处理时，如果可以判定评价指标是正向指标或逆向指标，则可以根据式(1)和式(2)分别对其进行归一化处理；但如果不能判定所有指标的指标特性，则可以对所有指标全部采用式(1)进行归一化处理，建立投影寻踪模型得到其权重若大于“0”，说明该指标为正向指标，其权重若小于“0”，说明该指标为逆向指标[11]。

(2)投影值的计算。设a=(a1,a2,…,ap)为投影方向，投影寻踪就是将x(i,j)投影到a上，得到一维投影值z(i)。

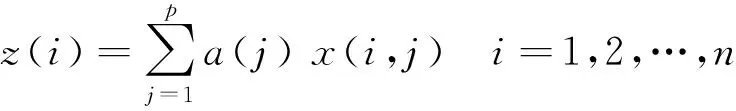
(3)

(3)构造投影指标函数Q(a)。

Q(a)=SzDz

(4)

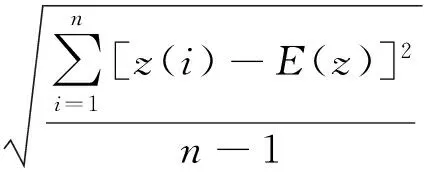
(5)

(6)

式中：Sz为投影值z(i)的标准差；Dz为投影值z(i)的局部密度；E(z)为序列{z(i)|i=1,2,…,n}的平均值；R为局部密度的窗口半径；r(i,j)为样本之间的距离；u(t)为单位阶跃函数。

R的选取原则是在窗口内的样本点不能过少，同时样本点个数增加时，在窗口内的样本点也不能增加太多[9]。目前没有系统的理论依据来确定窗口宽度，采用较普遍的是Friedman建议的密度窗宽取全部样本投影特征值方差的10%即0.1Sz。

不同的投影方向反映不同的数据结构特征，最佳投影方向就是最大可能暴露高维数据某类特征结构的投影方向，因此可以通过求解投影指标函数最大化问题来估计最佳投影方向，即：

最大化目标函数：

Q(a)=SzDz

(7)

约束条件：

(8)

这是一个有约束优化问题，本文采用罚函数法[12, 13]将其转化为一个无约束优化问题，则新的目标函数为：

最小化目标函数：

(9)

式中：h为惩罚因子。

式(9)是以a=(a1,a2,…,ap)为优化变量的非线性优化问题，用常规方法处理比较困难。

(4)粒子群算法优化投影指标函数。粒子群算法中每个粒子的位置都是优化问题的一个解，在迭代过程中每个粒子与粒子群的个体历史最优位置和全局最优位置进行比较，然后对自身位置进行综合调整使其不断接近最优位置，最终种群中所有粒子聚集的位置就是优化问题的解。

投影寻踪模型中的投影方向即为粒子群算法要优化的问题。设粒子的种群规模为N，第k(k=1,2,…,N)个粒子的速度和位置更新公式如下：

vk(t+1)=wvk(t)+c1r[pk(t)-ak(t)]+

c2r[g(t)-ak(t)]

(10)

ak(t+1)=ak(t)+vk(t+1)

(11)

式中：w为惯性权重因子；c1，c2为学习因子；r是介于[0,1]随机产生的数；p和g分别为粒子群的个体历史最优位置与全局最优位置。

个体历史最优位置是粒子迭代过程中适应值最好的位置，全局最优位置是整个粒子群迭代过程中适应值最好的位置，在投影寻踪优化问题中目标函数Q1(a)即为适应度函数用以计算适应度值。当算法达到预定迭代次数时，粒子群中所有粒子聚集的位置就是佳投影方向a*。

(5)优序排列。将得到的最佳投影方向a*代入式(3)后可得到各样本点的投影值z*(i)，将其值从大到小排序，则可以将其样本从优到劣进行排序。

2 基于粒子群算法的投影寻踪模型在水稻灌溉制度评价中的应用

水稻的需水量包括蒸腾、蒸发和土壤渗漏，土壤渗漏量与土壤水分状况密切相关，而灌溉对蒸腾量与蒸发量也有影响[14]，因此我们可以通过调节灌溉模式来减少水稻的耗水量。因此选取水层和土壤含水率[1]等因素作为决策变量，给出4种水分管理模式供选优分析，见表1。

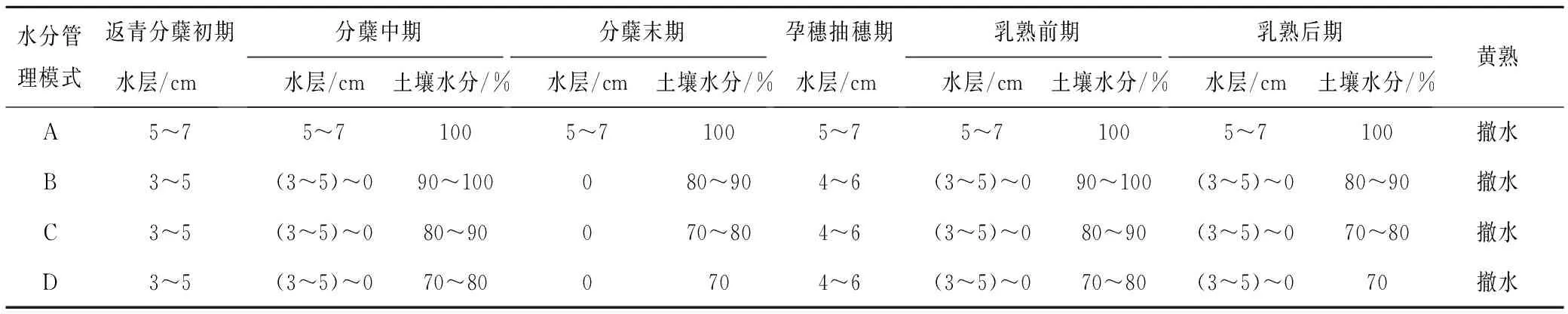
表1 不同生育阶段土壤水分调节模式

研究水稻灌溉模式的优劣性，可利用水稻在其生长发育过程中的表征作为评判标准，而水分调节对水稻的分蘖—幼穗分化和灌浆成熟(乳熟前后期)2个阶段影响显著，故对此2阶段的生育特征进行分析。

2.1 分蘖—幼穗分化阶段优化灌溉制度的投影寻踪模型

分蘖期为促进水稻生长、保证适当穗数、协调营养体上下结构、争取理想株型的关键时期[1]。生育特征的主要指标为有效分蘖率、有效茎数、叶面积指数、根活跃吸附面积、光能利用率、净同化率、生长量、生物量、相对生长率和消光系数等，从中选取10个主要的生育特征作为分析的状态变量，如表2所示。

依据由4种灌溉模式的10个状态变量构成的评价指标集建立基于粒子群算法的投影寻踪模型，通过粒子群算法优化投影值标函数以求取最佳投影方向，并通过最佳投影方向与评价指标的线型投影得到投影值，根据投影值的大小对水稻的4种灌溉模式进行综合评价。

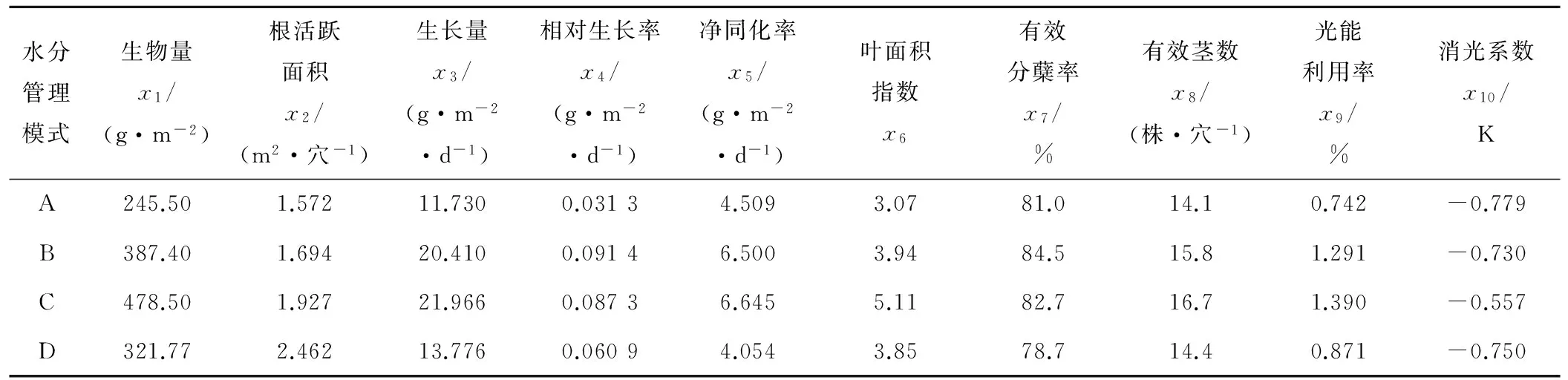
表2 分蘖—幼穗分化期的状态变量

利用MATLAB编制基于粒子群算法的投影寻踪模型程序并进行调试，将参数设置为：种群规模N=100，学习因子c1=c2=2，惩罚因子h=200，得出最大投影指标值为2.655 9，最佳投影方向a*=(0.313 7， -0.041 0，0.379 0，0.333 8，0.377 7，0.284 7，0.244 5，0.364 3，0.381 8，0.298 6)(见图1)。

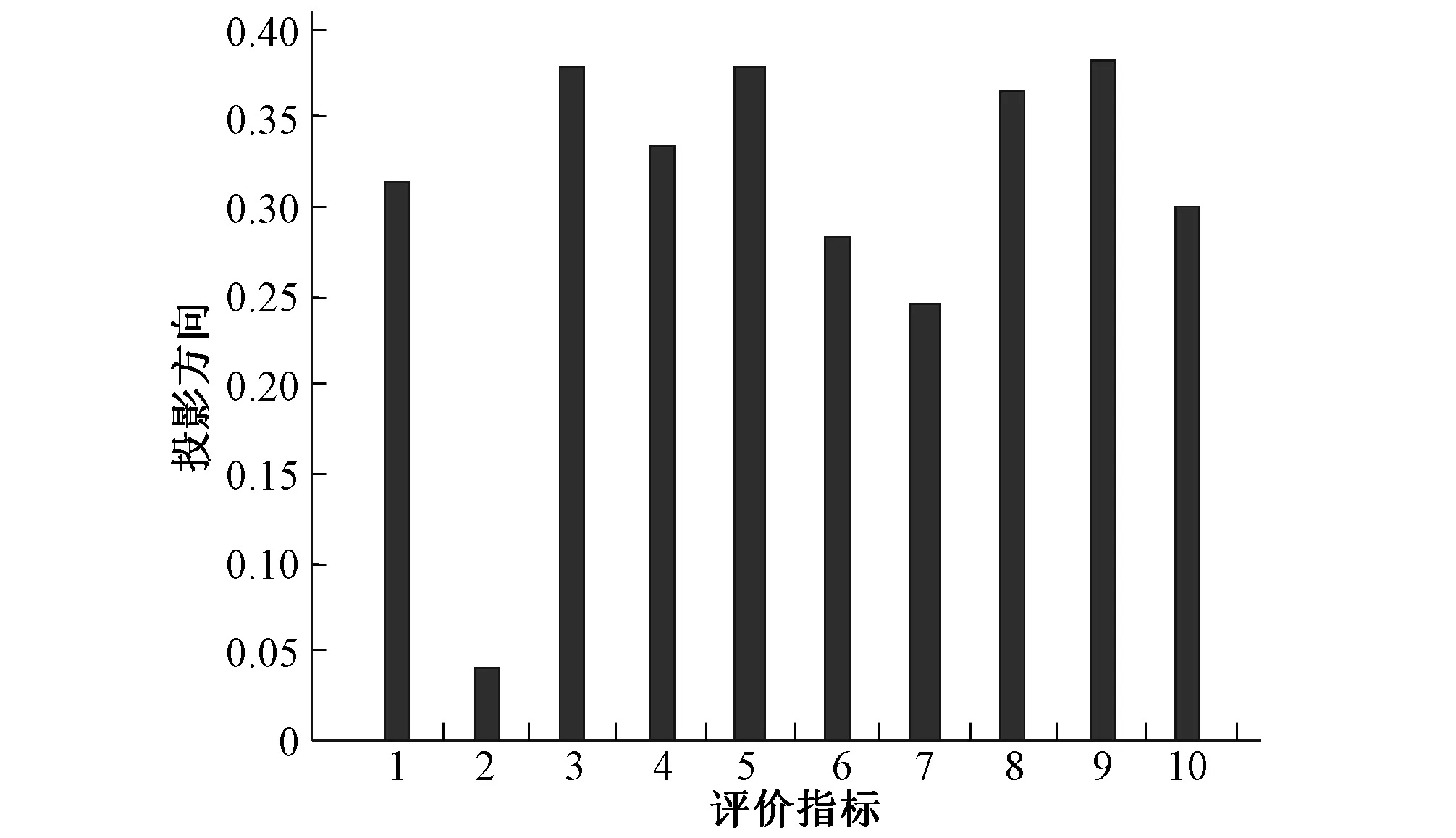
图1 分蘖期评价指标的投影方向a*

将a*代入式(3)后即得4种灌溉模式的投影值z*(j)=(0.163 2，2.190 4，2.863 3，0.567 8)，灌溉模式的优劣排序：模式C>模式B>模式D>模式A(见图2)。

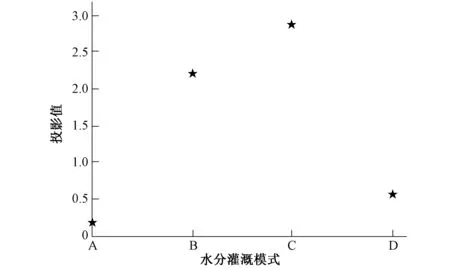
图2 分蘖期投影值z*(j)散布图

2.2 灌浆—成熟阶段水稻优化灌溉制度的投影寻踪模型

此期由前阶段营养生长以进入生殖生长，是通过光合作用进行籽实积累创造产量的关键时期[1]。这自然又与密度、根系发育状况、生长量和光能利用程度以及株型和生理特性等有关，故选取16个主要的生育特征作为判别灌溉技术优劣的指标，见表3。

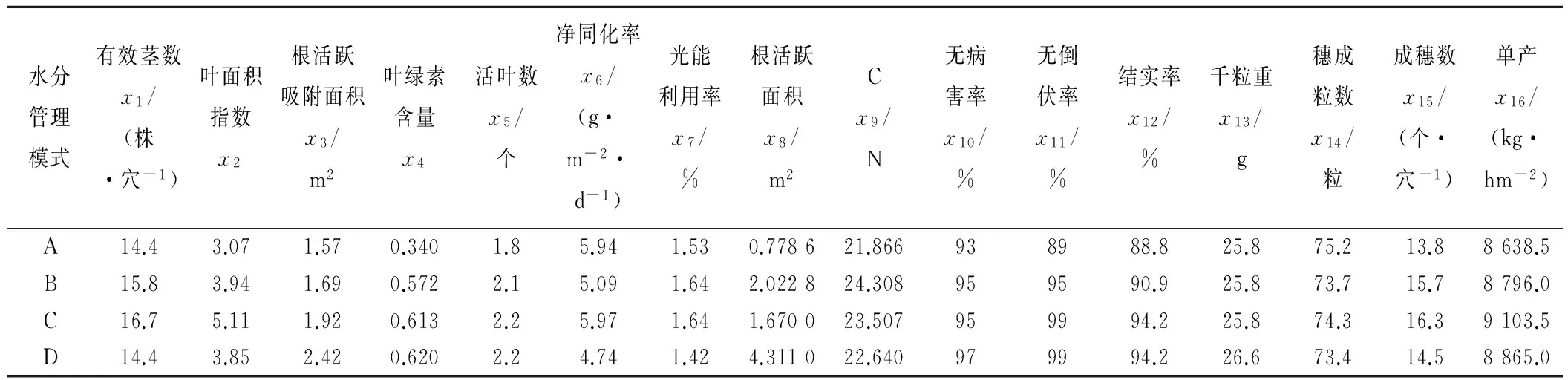
表3 生育后期的状态变量

同样根据表3构成的评价指标集建立基于粒子群算法的投影寻踪模型，编写程序并设置参数：种群规模N=100，学习因子c1=c2=2，惩罚因子h=200，得出最大投影指标值为2.895 7，a*=(0.246 8，0.280 4，0.206 8，0.350 6，0.342 1，-0.128 5，0.067 5，0.173 7，0.200 6，0.224 1，0.331 7，0.331 8，0.116 0，-0.235 5，0.271 1，0.284 6)(见图3)，z*(j)=(-0.327 1，1.853 1，2.627 3，2.490 6)，灌溉模式的优劣排序：模式C>模式D>模式B>模式A(见图4)。

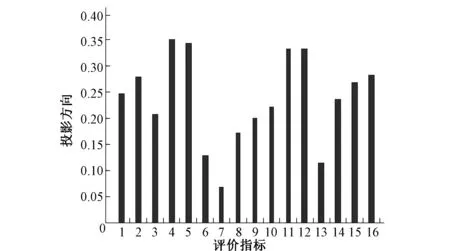
图3 灌浆期评价指标的投影方向a*

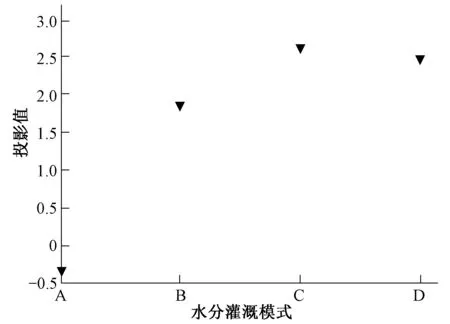
图4 灌浆期投影值z*(j)散布图

以上两小节对水稻的分蘖和灌浆2个阶段分别建立了基于粒子群算法的投影寻踪模型，综合评判出最佳灌溉模式都为模式C，与实际实验结果一致，评价结果客观、准确，表明该模型具有很强的准确性与可行性。

3 结 语

本文将基于粒子群算法的投影寻踪模型应用到水稻灌溉制度评价中，利用水稻分蘖期或灌浆期的多个生育特征构成的评价指标集寻求最佳投影方向即确定各评价指标的贡献度，最终根据评价指标在该投影方向线型投影得到的投影值大小进行水稻灌溉制度的综合评价，避免了专家赋权的人为干扰，且评价结果科学合理，方法切实可行，为农业灌溉系统等方面的研究提供一条新途径。

[1] 杨 娜, 付 强, 李荣东, 等. 连续蚁群算法在水稻灌溉制度优化中的应用 [J]. 农业工程学报, 2010,26(13):134-138.

[2] 邢权兴, 孙 虎, 管 滨, 等. 基于模糊综合评价法的西安市免费公园游客满意度评价[J]. 资源科学, 2014,36(8):1 645-1 651.

[3] 陈晓红, 杨志慧. 基于改进模糊综合评价法的信用评估体系研究----以我国中小上市公司为样本的实证研究[J]. 中国管理科学, 2015,23(1):146-153.

[4] 项海飞. 多属性群决策中综合权重调整算法研究[J]. 统计与决策, 2013,(8):23-25.

[5] 李晴新, 朱 琳, 陈中智. 灰色系统法评价近海海洋生态系统健康[J].南开大学学报(自然科学版), 2010,43(1):39-43.

[6] Li L, Li D. Fuzzy entropy image segmentation based on particle swarm optimization[J]. Progress in Natural Science, 2008,18(9):1 167-1 171.

[7] 欧阳森, 石怡理. 改进熵权法及其在电能质量评估中的应用[J]. 电力系统自动化, 2013,37(21):156-159.

[8] Zhang H, Wang C, Fan W. A projection pursuit dynamic cluster model based on a memetic algorithm[J]. Tsinghua Science and Technology, 2015,20(6):661-671.

[9] 姜秋香, 付 强, 王子龙. 基于粒子群优化投影寻踪模型的区域土地资源承载力综合评价[J]. 农业工程学报, 2011,27(11):319-324.

[10] Liu Y L, Liu D F, Liu Y F, et al. Rural land use spatial allocation in the semiarid loess hilly area in China: Using a Particle Swarm Optimization model equipped with multi-objective optimization techniques[J]. Science China Earth Sciences, 2012,55(7):1 166-1 177.

[11] 楼文高, 乔 龙. 投影寻踪分类建模理论的新探索与实证研究[J]. 数理统计与管理, 2015,34(1):47-58.

[12] 崔承刚, 杨晓飞. 基于内部罚函数的进化算法求解约束优化问题[J]. 软件学报, 2015,26(7):1 688-1 699.

[13] 李志刚, 吴文传, 张伯明, 等. 一种基于高斯罚函数的大规模无功优化离散变量处理方法[J]. 中国电机工程学报, 2013,33(4):68-76.

[14] 王建鹏, 崔远来. 水稻灌区水量转化模型及其模拟效率分析[J]. 农业工程学报, 2011,27(1):22-28.