基于多场耦合模型的粉煤灰混凝土水化特性的数值研究

刘浩杰，周 伟，冯楚桥，常晓林，马 刚

(1. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2. 武汉大学 水工岩石力学教育部重点实验室，武汉 430072)

大体积混凝土在国家基础设施建设中有着广泛的应用，如何防止裂缝的形成和发展是工程中的关键技术问题，也是学术界研究的热点之一。温度变形是导致混凝土开裂的主要原因之一，因此深入研究混凝土的水化放热十分重要[1]。然而目前国内对混凝土水化放热的研究和应用多停留在线性理论的基础上，认为混凝土的水化反应放热过程仅与龄期有关[2]，忽略或简化了温度等因素的影响，造成仿真计算的偏差，因此有必要综合考虑龄期和温度等因素的影响来研究混凝土水化反应过程。

考虑用水化度作为中间变量来指示水化反应和混凝土性能发展的程度，发展成为研究混凝土水化反应过程及性能演变领域的热点。国内外学者在这方面已经做了一些研究[3-9]。Cervera等人[10,11]提出了早期混凝土热学-化学-力学耦合的有限元模型，可以用来研究随时间变化的水化度和水化热。Lackner等人[12]发现了水化度和材料固有断裂能函数之间的线性关系。Di Luzio和Cusatis[13,14]考虑了多种化学反应过程，提出了一个新的高性能混凝土的水化-热学-化学模型用以分析水分传输和热交换。张子明等人[15-17]基于等效时间对混凝土绝热温升、热传导方程、混凝土的徐变等进行了研究；马跃峰[18]研究了基于水化度的混凝土温度与应力；周伟等人[19]提出了新的考虑化学-热学-力学耦合效应的混凝土水化模型，研究了超硫酸盐水泥在大体积混凝土中适用性。

混凝土材料本身的性质对于裂缝的产生和发展同样有至关重要的影响，选用合适的混凝土材料能够很大程度上防止裂缝的产生。近年来在大体积混凝土中，使用工业废弃物粉煤灰取代部分水泥熟料的应用日益广泛[20]。使用粉煤灰混凝土除了具有节能减排、保护环境的优点外，其较低的水化放热量对温控防裂也发挥着积极的作用[21]。然而目前对粉煤灰混凝土的研究多停留在试验的阶段，因此有必要实现对粉煤灰混凝土水化反应过程的数值模拟。

本文采用热学-化学-力学耦合的水化模型模拟混凝土的温度过程，并在有限元方法中实现了早龄期混凝土热-力耦合的数值模拟。在有限元计算的参数研究中，采用适用于各向异性材料的均值化方法来估算混凝土的比热系数和导热系数。借助已有不同水胶比的粉煤灰混凝土试样的绝热温升试验数据，验证了水化模型的正确性并研究了粉煤灰混凝土的水化特性。考虑实际工程情况，在不同的温度边界下模拟了不同水胶比的粉煤灰混凝土的水化反应过程。

1 热学-化学-力学耦合模型

1.1 常用模型

1.1.1 水化热

目前常规方法在计算混凝土的水化热时采用绝热温升模型，认为水化热是一个以水化时间为变量的函数。对于大体积混凝土结构来说，工程实际中最常用的模型是[22]：

Q(t)=Q∞(1-e-atb)

(1)

式中：Q(t)是时间t时的水化热；Q∞是最终水化热；a、b是材料参数，可以通过绝热试验数据进行率定。

从水泥水化动力学的观点来看，水泥水化在绝热条件开始反应迅速，但在28 d后绝热温升的变化很小[23]。所以采用上述模型的缺点是在28 d后的水化热比实际偏大。

1.1.2 弹性模量

常规方法中，大体积混凝土的弹性模量随时间的发展过程可表示为：

E(t)=E∞(1-e-αtβ)

(2)

式中：E(t)是时间t时的水化热；E∞是最终弹性模量；α、β是材料参数。

1.2 长期的水化模型

混凝土的放热反应是由于水和水泥净浆发生反应产生的，为了描述这种反应的程度，定义了水化度的概念：

(3)

式中：m∞是假定水化反应中自由水充分反应，理想条件下结合水的最终质量；m(t)是时间t时结合水的质量。

根据阿伦尼乌斯定律[24]，水化过程可由式(4)描述。在这一模型中，水化反应速率与温度以及化学亲和力Aξ(ξ)相关：

(4)

式中：Ea是水化反应的活化能；Aξ(ξ)是化学亲和力；R是理想气体常数。

热-化学系统的自由能可以分为3个部分，热能、化学能、热-化学耦合部分。Cervera等人基于热力学观点推导了化学反应亲和力的标准化形式，假设化学能为水化反应程度的三次函数推导出化学反应亲和力Aξ(ξ)的形式，文献[25,19]基于对混凝土水化反应的基于认识，对该假设做出小的修改，假设化学能为水化反应程度的四次函数：

(5)

1.3 瞬时传热过程

混凝土为各向同性热传导，水化过程可视作为内热源，瞬时传热过程可按下式描述：

(7)

式中：ρ是密度；C是体积热容量；λT是导热系数；Δ是拉普拉斯算子；Q∞是最终单位质量水化热。优于混凝土温度水平影响其水化热的释放，因此，由水化造成的混凝土潜热的释放实质上是非线性且热相关的过程。

1.4 热学性质和力学性质

合理地选取参数是水化过程数值模拟的关键先决条件，关于用在细观模型的混凝土热学参数的研究记载几乎没有，本文采用一个能较好适用于各向异性材料的多尺度平均化方法来推求热学计算参数[26]。根据De Schutter等人[27]研究成果，估算混凝土的弹性模量、抗压强度和泊松比。

1.4.1 比热容

已知水泥、水、骨料的比热容和体积分数，模型的比热容可以用下面公式估算[26]：

(8)

式中：cfp,cwater,ccement,cp(ξ),cconcrete,cagg,cfiller分别指的是(每单位体积)的新拌水泥浆体、水、水泥、水化过程中的浆体、混凝土、骨料和添加剂的比热容；fwater、fcement、fp、fagg、ffiller分别指的是水、水泥、浆体、骨料、添加剂的体积分数；A、B是材料常数，随着水灰比的不同，在0.3～0.5之间变化。

1.4.2 导热系数

砂浆是由水和胶凝材料组成，可采用经典的Hashin-Shtrikman边界来估算导热系数。估算值由实验测得的导热系数(λ1、λ2)和体积分数(f1、f2)得到。对于λ2≥λ1Hashin-Shtrikman的下边界λ1和上边界λu由下面两个公式得到[26]：

(9)

两相复合材料的有效导热系数λhom取H-S上下界限的平均值：

(10)

根据文献[27]，水泥净浆的导热系数是一个关于体积分数的函数，因此，本文不考虑导热系数的非线性特性。

1.4.3 弹性模量

(11)

式中：E(ξ)是水化度为ξ时的弹性模量；ξ0是混凝土加载龄期时的水化度；E∞是水化度为1时的弹性模量；re是从实验数据中获取的常数。

1.4.4 抗压强度

(12)

式中：f(ξ)是水化度为ξ时的抗压强度；ξ0是混凝土加载龄期时的水化度；f∞是水化度为1时的抗压强度；rf是从实验数据中获取的常数。

1.4.5 泊松比

(13)

式中：μ(ξ)是水化度为ξ时的泊松比；μ∞是水化度为1时的泊松比。

2 验 证

2.1 水化度模型的校核方法

本文采用水化度或温度作为中间参数，决定混凝土的热学性能和力学性能。在本节中，将借助已有实验数据率定水化度模型中的相关参数，并进一步验证上述模型。

混凝土水化反应的热力学参数可以结合绝热温升实验得到的温度变化数据或水化放热速率数据，结合以下公式推导得出：

(15)

式中：Q是水化放热量；Q∞是最终水化放热量；ξ(t)是时间t时的水化度；t0.5是水化度为0.5时的时间；t0是诱导期结束的时间。

2.2 超硫酸盐水泥(SSC)和普通硅酸盐水泥(OC)

刘数华等人[28]就超硫酸盐水泥的水化特性进行了研究，发现了水泥细度对水泥水化放热速率的影响。笔者结合该研究中的水化实验数据[28]，运用公式(14)、(15)，率定水化模型参数，并采用热学-化学-力学水化度模型模拟了超硫酸盐水泥试样和普通硅酸盐水泥试样的水化反应过程。表1是超硫酸盐水泥净浆和普通硅酸盐水泥净浆的水化模型参数。图1是采用水化模型模拟的普通硅酸盐水泥和超硫酸盐水泥的累计放热量模拟值与实验值的对比图；模拟值与实验值吻合(误差在2%之内)。

刘数华等人的研究表明[28]，超硫酸盐水泥的水化特性与普通硅酸盐水泥的水化特性有很大不同；超硫酸盐水泥水化放热量明显低于普通硅酸盐水泥；由于超硫酸盐水泥体系在大量使用矿渣时需要一定的碱度环境，这导致超硫酸盐水泥的第二放热峰出现的时间比普通硅酸盐水泥晚。

由图1可以看出：普通硅酸盐水泥样本的累计放热量稳定在170 J/g附近，而超硫酸盐水泥样本SSC1、SSC2、SSC3的累计放热量分别稳定在60，75，90 J/g附近；普通硅酸盐水泥样本的第二放热峰大约出现在6 h，超硫酸盐水泥SSC1、SSC2、SSC3的第二放热峰大约出现在30、25、20 h；对于不同比表面积的超硫酸盐水泥而言，比表面积越高，累计放热量越高，第二放热峰出现的时间越早；水化度模型的数值模拟结果符合上述研究规律。

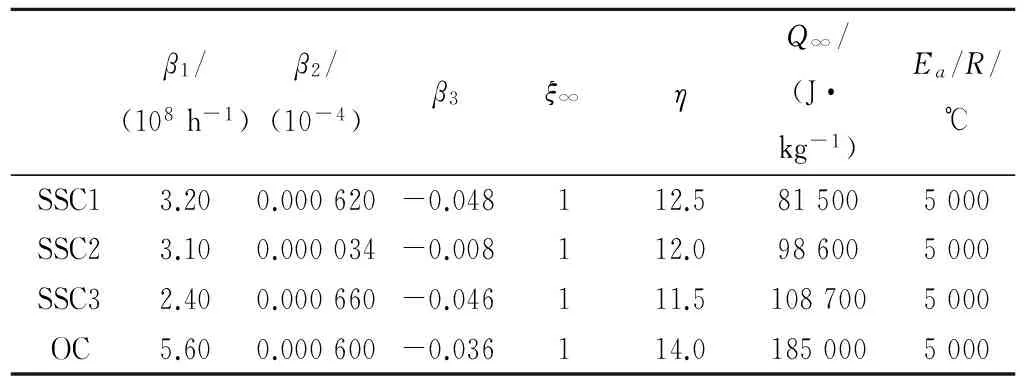
表1 普通硅酸盐水泥净浆和超硫酸盐水泥净浆的水化度模型参数Tab.1 Parameters of the hydration model of OC and SSC paste

图1 绝热条件下普通硅酸盐净浆和超硫酸盐净浆的累计放热量曲线Fig.1 Hydration heat quantity curves for adiabatic test of OC and SSC

已知水化反应中水泥净浆的水化模型参数(表1)和混凝土组分(表2)，便可研究超硫酸盐净浆的水化特性。假定骨料对水化反应没有影响，那么最终水化放热量可以用下式估算：

Q∞=Qe∞fcement

(16)

式中：Qe∞是水泥净浆的最终水化放热量；fcement是水泥净浆在混凝土中的体积分数。

图2是等温条件下普通硅酸盐净浆和超硫酸盐净浆抗压强度曲线。

2.3 粉煤灰混凝土

选用大岗山水电站实际工程中粉煤灰混凝土样本数据，运用公式(14)、(15)，将温度上升过程的模拟值与粉煤灰混凝土样本的绝热温升实验值对比如图3，结果显示水化度模型数值模拟的结果符合实验值(误差小于2%)。表2为四种不同水胶比的粉煤灰混凝土试样具体配合比，表3为不同组成材料的热学参数，表4列举了水化度模型校核后的参数结果。

混凝土的力学实验通常是在等温条件下进行的，因此水化反应也是在等温条件下模拟的，这样混凝土的力学特性便能与水化度保持相关。四种粉煤灰混凝土的弹性模量和泊松比随水化度的变化曲线如图4。

图2 等温条件下普通硅酸盐净浆(OC)和超硫酸盐净浆(SSC)的抗压强度曲线Fig.2 Compressive strength evolution for isothermal test of OC and SSC

表2 四种粉煤灰混凝土配合比Tab.2 Mix proportion of fly ash concrete

表3 不同组成材料的热学参数Tab.3 Thermal parameters of the components

表4 四种粉煤灰混凝土的水化度模型参数Tab.4 Parameters for the hydro-thermal model of fly ash concrete

3 温度边界对水化进程的影响

实际工程中，就某一混凝土结构而言，不同结构部位由于散热条件不同，温度边界条件不同，其水化速率也有快有慢，表面混凝土与外界气温相接触，气温变化幅度不大时，温度条件接近等温条件，内部混凝土不与外界环境接触，散热条件较差，温度条件接近绝热条件，因此在不同温度边界下模拟混凝土的水化反应对实际工程具有指导意义。本文分别在等温条件和绝热条件下模拟了四种不同水胶比的粉煤灰混凝土试样的水化反应过程。图5是4种粉煤灰混凝土试样水化度和弹性模量历程曲线。

图3 绝热条件下粉煤灰混凝土的温度历程曲线Fig.3 Temperature evolution for adiabatic test of fly ash concrete

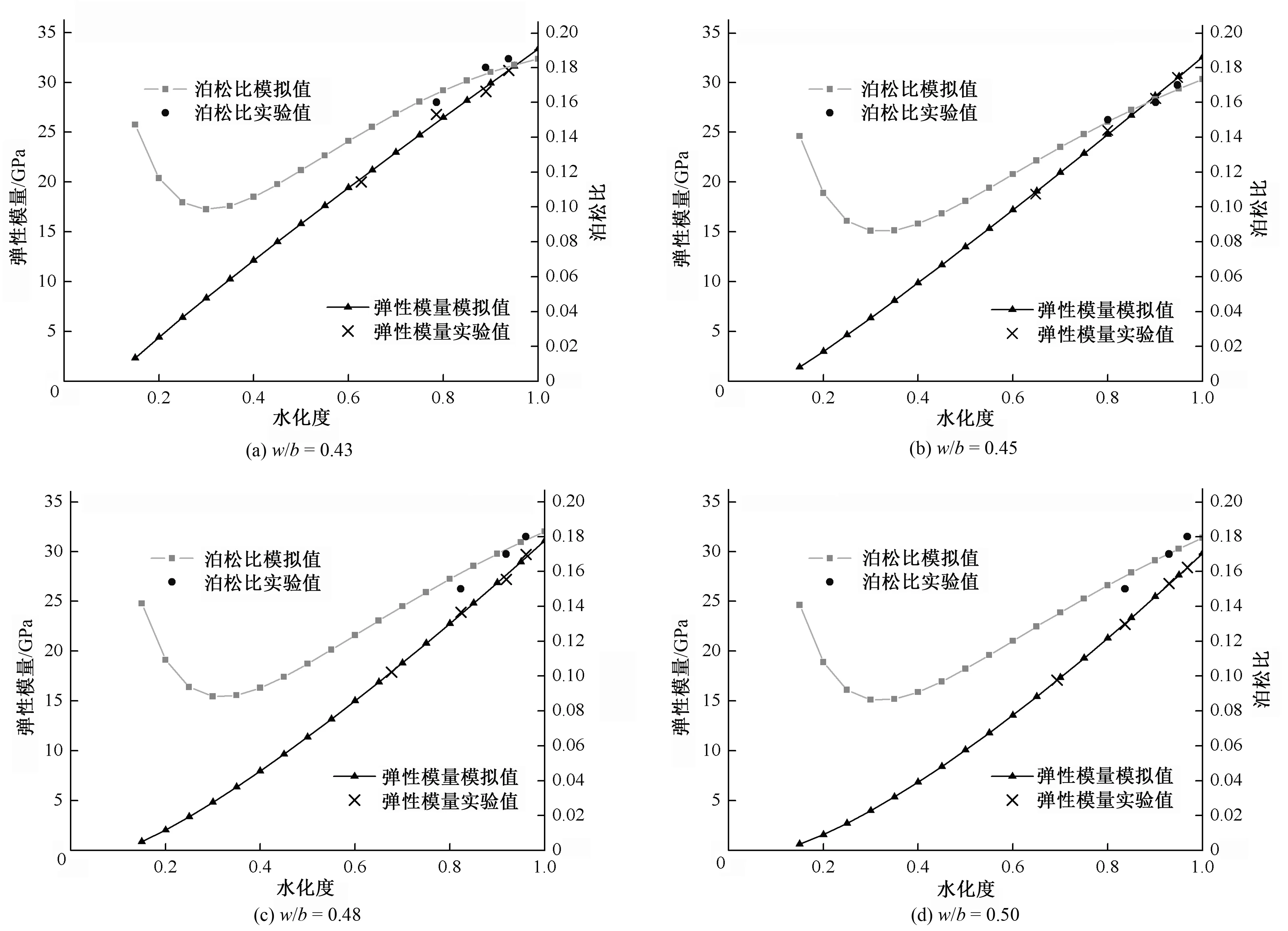
图4 等温条件下粉煤灰混凝土弹性模量与泊松比的历程曲线Fig.4 Young’s modulus and Poisson’s ratio evolution for isothermal test of fly ash concrete

图5 等温条件和绝热条件下粉煤灰混凝土水化度和弹性模量历程曲线Fig.5 The degree of hydration and Young’s modulus evolution for isothermal and adiabatic test of fly ash concrete

由图5可知相同龄期两种条件下水化反应过程差异明显，在水化反应迅速的前28 d，绝热条件下混凝土的水化度明显高于等温条件下的水化反应度，随后，两种温度边界下水化度差异逐渐减少，但在模拟的180 d龄期内，相同龄期绝热条件下的水化度均高于等温条件下的水化度，说明在180 d龄期内相同龄期绝热条件下混凝土的水化反应速率高于等温条件下混凝土的水化反应速率。

同样地，体现在弹性模量的模拟值上，在180 d龄期内，相同龄期绝热条件下混凝土的弹性模量均高于等温条件下的弹性模量。

4 结 语

针对常规温度预测模型的缺点，本文采用热学-化学-力学耦合的水化模型，进行了早龄期混凝土热-力耦合现象的有限元数值模拟和参数研究。主要结论如下。

(1)常规计算方法在处理混凝土温度变化过程时只考虑了龄期的影响，忽视了反应温度等其他因素的影响。为了解决该问题，结合之前学者的研究，运用热学-化学-力学的水化模型模拟了混凝土的温度过程。

(2)采用适用于各向异性材料的均化方法估算混凝土的比热系数和导热系数，对比物理实验结果，数值模拟的结果显示混凝土的水化过程能被精确模拟。

(3)考虑实际工程情况，在不同温度边界下(等温条件和绝热条件)，运用该耦合模型模拟了4种不同水胶比的粉煤灰混凝土试样的水化反应过程。在180 d龄期内，相同龄期绝热条件下的混凝土试样水化度均高于等温条件下的水化度，相应地，其弹性模量也较高。

□

[1] Benboudjema F, Torrenti J M. Early-age behaviour of concrete nuclear containments[J]. Nuclear Engineering & Design, 2008,238(10):2 495-2 506.

[2] Chu I, Lee Y, Amin M.N, et al. Application of a thermal stress device for the prediction of stresses due to hydration heat in mass concrete structure[J]. Constr. Build. Mater, 2013,45:192-198.

[3] Waller V, D’Aloïa L, Cussigh F, et al. Using the maturity method in concrete cracking control at early ages[J]. Cem. Concr. Compos, 2004,26:589-599.

[4] Gasch T, Malm R, Ansell A. A coupled hygro-thermo-mechanical model for concrete subjected to variable environmental conditions[J]. International Journal of Solids & Structures, 2016,91:143-156.

[5] Zreiki J, Bouchelaghem F, Chaouche M. Early-age behavior of concrete in massive structures, experimentation and modelling[J]. Nucl. Eng. Des., 2010,240:2 643-2 654.

[6] Wang X, Cho H, Lee H. Prediction of temperature distribution in concrete incorporating fly ash or slag using a hydration model[J]. Compos. Part B Eng., 2011,42:27-40.

[7] Thomas J J, Biernacki J J, Bullard, J W Bishnoi, et al. Modeling and simulation of cement hydration kinetics and microstructure development[J]. Cem. Concr. Res., 2011,41:1 257-1 278.

[8] Martinelli E, Koenders E A B, Caggiano A. A numerical recipe for modelling hydration and heat flow in hardening concrete[J]. Cem. Concr. Compos, 2013,40:48-58.

[9] De Freitas J A T, Cuong P T, Faria R, et al. Modelling of cement hydration in concrete structures with hybrid finite elements[J]. Finite Elem. Anal. Des, 2013,77:16-30.

[10] Cervera M, Faria R, Oliver J, et al. Numerical modelling of concrete curing, regarding hydration and temperature phenomena[J]. Comput. Struct, 2002,80:1 511-1 521.

[11] Cervera M, Oliver J, Prato T. Thermo-chemo-mechanical model for concrete. I: Hydration and aging[J].J. Eng. Mech, 1999,125:1 018-1 027.

[12] Lackner R, Mang H A. Chemoplastic material model for the simulation of early-age cracking: From the constitutive law to numerical analyses of massive concrete structures[J]. Cem. Concr. Compos, 2004,26:551-562.

[13] Di Luzio G, Cusatis G. Hygro-thermo-chemical modeling of high performance concrete. I: Theory[J].Cem. Concr. Compos, 2009,31:301-308.

[14] Di Luzio G, Cusatis G. Hygro-thermo-chemical modeling of high-performance concrete. II: Numerical implementation, calibration, and validation[J]. Cem. Concr. Compos, 2009,31:309-324.

[15] 张子明，宋智通，黄海燕. 混凝土绝热温升和热传导方程的新理论[J].河海大学学报，2002,30(3):1-5.

[16] 张子明，冯树荣，石青春，等. 基于等效时间的混凝土绝热温升[J].河海大学学报：自然科学版，2004,32(5):573-577.

[17] 张子明，周红军，殷 波. 基于等效时间的混凝土徐变[J]. 河海大学学报：自然科学版， 2005,33(2):173-176.

[18] 马跃峰. 基于水化度的混凝土温度与应力研究[D]. 南京：河海大学，2006.

[19] Wei Zhou, Chuqiao Feng, Xinghong Liu, et al. Contrastive numerical investigations on thermo-structural behaviors in mass concrete with various cements[J]. Materials, 2016,9:377-396.

[20] 雷 瑞，付东升，李国法等. 粉煤灰综合利用研究进展[J]. 洁净煤技术，2013,19(3):106-109.

[21] 刘数华, 方坤河. 粉煤灰综合利用现状综述[J]. 福建建材，2008,103(2),8-10.

[22] Zhu B F. Thermal Stresses and Temperature Control of Mass Concrete[C]∥ Tsinghua University Press: Beijing, China, 2014.

[23] Yang J, Hu Y, Zuo Z, et al. Thermal analysis of mass concrete embedded with double-layer staggered heterogeneous cooling water pipes[J]. Appl. Therm. Eng., 2012,35:145-156.

[24] Ulm F J, Coussy O. Modeling of thermos-chemo-mechanical couplings of concrete at early ages[J]. J Eng Mech(ASCE), 1995,121(4):717-26.

[25] Zhou W, Feng C, Liu X, et al. A macro-meso chemo-physical analysis of early-age concrete based on a fixed hydration model[J]. Mag. Concr. Res., 2016.

[26] Bentz D P. Transient plane source measurements of the thermal properties of hydrating cement pastes.Mater[J]. Struct., 2007,40:1 073-1 080.

[27] De Schutter G. Degree of hydration based Kelvin model for the basic creep of early age concrete. Mater[J]. Struct.,1999,32:260-265.

[28] Liu S, Wang L, Gao Y, et al. Influence of fineness on hydration kinetics of supersulfated cement.Thermochim[J]. Acta, 2015, 605:37-42.