基于VOF的弧底梯形短喉道量水槽水力性能研究
2017-03-21马孝义景志芳甘学涛
张 敏,马孝义,景志芳,柳 烨,甘学涛
(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)
水作为生命之源,与人类活动、社会发展紧密相连。目前我国的农业灌溉水利用系数平均不足0.5,节水空间很大。随着经济的发展及水资源的日益紧张,为了促进农业节水、实现水资源的可持续发展,加强灌区量水工作,对灌区用水进行有效的控制和精确的量测变得十分重要[1,2]。弧底梯形渠道由于结构简单,整体性强,水流条件好,过流顺畅,底部的弧形能够有效减少渠道淤积,降低工程维护费用,且抗冻胀性好,因此适宜在北方渠道大规模应用。针对弧底梯形渠道量水设备不足的现状[3,4],选定结构简单、经济适用、测量精度高的量水设施尤为重要。
R.L.Parshall[5]在文丘里槽[6]基础上研制出巴歇尔量水槽,它由短直喉道、上游收缩段和下游扩散段三部分组成,该槽具有壅水高度低,量水精度高,测流幅度大,水头损失小,不易淤积等特点,是近年来使用较广泛的短喉道槽,但其因结构复杂,会造成施工困难。Blaisdel[7]对Parshall的测流数据和流量公式进行深入分析,得出其测流相对误差在 5%以内。李杰[8]等对自由和淹没出流情况下量水槽的水位流量关系及冲沙情况等水力性能进行了研究。李香平[9]等将巴歇尔量水槽斜槽底变为水平,并对测流范围进行重新标定。以某灌区灌溉渠系改造工程为原型,笔者在巴歇尔量水槽基础上进行改造,提出了与之配套的弧底梯形短喉道式量水槽。对其在不同底坡、喉道长度及收缩比条件下的水力性能进行研究,并对其影响因素进行分析,以期为新型量水槽的推广应用提供一定的参考。
1 量水槽体型设计
1.1 量水槽结构
弧底梯形短喉道量水槽由进口收缩段、喉道段、出口扩散段三部分组成,其中进口收缩段呈3∶1收缩,出口扩散段呈6∶1扩散。通过调整喉口断面弧底半径R、喉口边坡系数m,使水流产生局部收缩,并在收缩段产生临界流,由稳定的水位流量单值函数关系得到过槽流量,达到测流目的。收缩比ε=A0/A,A0为量水槽喉口断面面积,A为渠道断面面积。短喉道量水槽由于增加了喉道段长度使水流流态变化得到缓冲,能够较为平稳的衔接,能更精确确定上游水深断面位置,且由于水流内部掺混作用的加强,使得流速分布更趋于均匀化分布。量水槽结构示意图如图1。

图中:W为量水槽喉宽;a为喉长;L+a为量水槽长度;B为渠道顶宽;h为渠槽水位。图1 弧底梯形渠道短喉道量水槽结构示意图Fig.1 Structure of arc-based trapezoidal canal and short-throat flow measurement flume
1.2 量水槽尺寸设计
本文对收缩比ε=0.61,0.65,0.7的量水槽在不同喉道长度a=0,0.25,0.5,1 m下弗劳德数、水头损失、水面线等的变化进行了模拟分析。渠道参数及数值试验方案如表1所示。

表1 量水槽尺寸设计方案Tab.1 Dimension design scheme of arc-based trapezoidal and measuring flume
1.3 设计流量
弧底梯形渠道设计流量Q为设计水位下的渠道流量,可按下式计算:
(1)
式中:Q为渠道设计流量;A为渠道断面面积,R为底弧半径;C为谢才系数;i为渠道底坡。
2 量水槽数学模型
2.1 控制方程
弧底梯形短喉道量水槽测流为不可压缩黏性流体运动,根据基本物理守恒定律,过槽流量为牛顿流体,则测流方程为连续性方程和Navier-Stokes方程[10]。
连续性方程:
(2)
式中:ρ为流体密度,本文中取1 000 kg/m3;t为时间;ui为沿i(i为笛卡儿坐标中的x、y或z)方向的速度分量;xi为沿i方向的坐标分量。
Navier-Stokes方程:
(3)
式中:ui、uj分别为沿i和j方向速度分量;xi、xj分别为沿i和j方向的坐标分量;p为压力;μ为分子黏性系数;μ′i、μ′j为各脉动流速分量。
本文研究的弧底梯形渠道短喉道量水槽过槽水流属于具有高雷诺数的湍流,因此选择RNGk-ε模型进行湍流数值模拟,使控制方程组封闭的同时因考虑湍流漩涡而有效改善了精度。湍流脉动的动能k和耗散率ε如下:
湍动能k方程:
(4)
其中:
式中:μ为动力黏滞系数,N·s/m2;μt为湍动黏度,Cμ=0.084 5;μeff=μ+μt,N·s/m2;Gk为平均速度引起的紊动能产生项,αk=1.39。
湍动耗散率ε方程:
(5)

2.2 三维模型建立、网格划分与边界条件设置
本研究用Matlab进行量水槽选型,Autocad实现三维建模,联合Gambit完成网格划分。渠道上下游边界长度变化会导致网格数发生变化,从而对计算时长和计算精度产生影响。通过试验可得,选取的上游渠段过短,难以消除水面跌落对测流精度的影响[4]。理论上得知,上下游渠道长度越长,计算精度就越高,但随着计算长度的增加,计算域内的网格单元数会大幅增加,其计算时间也就越长,效率也越低。因此从实际情况出发,在兼顾精度和计算时长的关系的前提下,分别采用5种不同上下游渠道长度弧底梯形短喉道量水槽对计算域进行网格划分[11]。实验结果见表2,综合考虑,数值模拟选取渠道长250 m左右,以量水槽为零点,上游取200 m,下游取50 m,能够得到更加逼真的模拟渠道流态,减小上下游边界对计算域的影响。
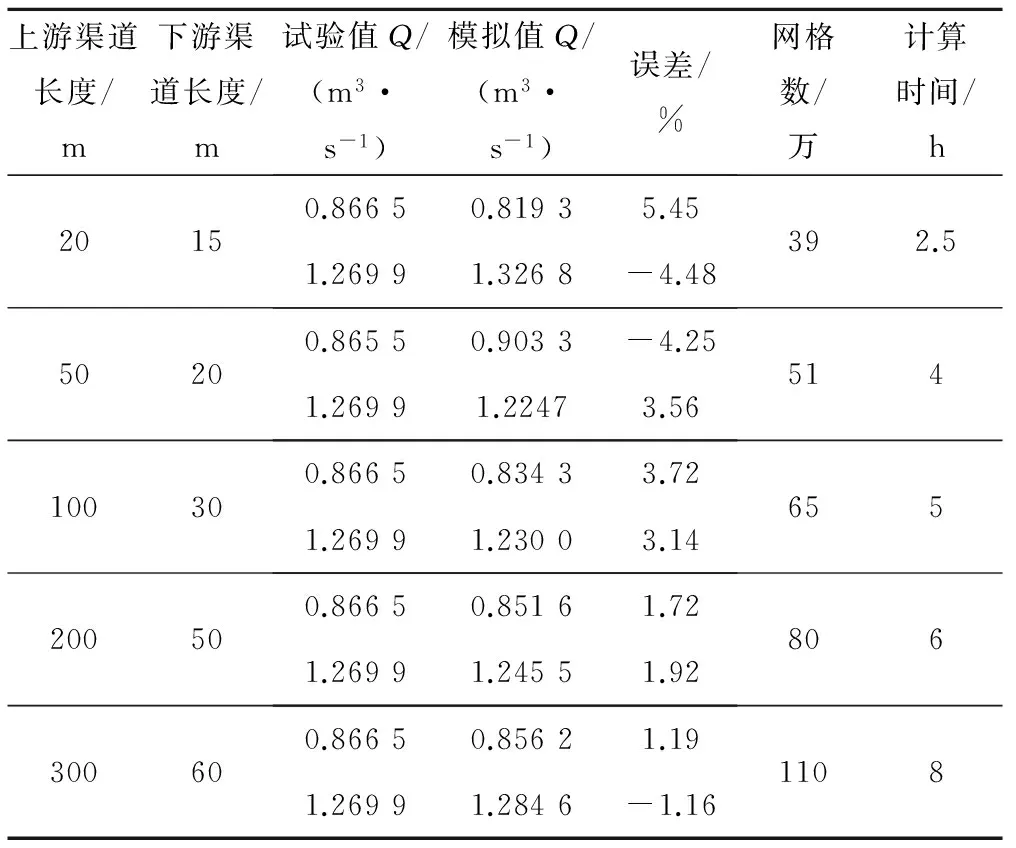
表2 上下游不同边界长度对计算影响Tab.2 The influence of different boundary lengths on the calculation of the upper and lower reaches
建模时,坐标原点为渠道进口断面圆弧中点,取顺水流方向为x轴(顺水流为正),宽度方向为y轴(河道左岸为正),高度方向为z轴(向上为正)。在量水槽段采用非结构网格,并进行局部加密,其高适应性与量水槽段复杂流动域结构更为匹配,渠道段采用结构网格,因渠道左右对称,可取一半计算域,网格总数约8.0×105,量水槽尺寸见表1,边界条件设置如下:进口边界由空气进口和水流进口二部分组成,空气进口边界条件设置Pressure Inlet,水流进口设置为Velocity Inlet,出口设置为Pressure Outlet,渠道断面中心面取对称面Symmetry,渠道的整个底部以及边壁选择固壁边界条件wall,并设置无滑移选项,采用标准的壁面函数法处理,模型网格划分如图2。

图2 弧底梯形短喉道量水槽模型与网格划分Fig.2 Model and mesh division of arc-based trapezoidal canal and short-throat flow measurement flume
3 量水槽计算方法与模拟结果分析
3.1 计算方法
本文采用RNGk-ε湍流模型,它将非稳态Navier-Stokes方程对一个平衡态作Gauss统计展开,并用对脉动频谱的波数段作滤波的方法,从理论上导出高Re数k-ε模型,所得出的k-ε方程形式上同标准k-ε模型完全一样,但不同的是5个系数之值不是根据实验数据而是由理论分析得出,因而在计算复杂的流动方面,理论上精度要高于标准的k-ε模型[12]。本研究通过VOF方法跟踪自由表面,水流从入口流入渠槽直至出口, 通过对体积分数的迭代求解,就能够自动生成水气的交界面,设置监视器中Mass Flow Rate选项,当其值接近于0且基本保持不变,认为计算收敛。采用CFD软件之Fluent6.3对建立好的三维模型进行仿真计算[13]。
3.2 流态分析与水面线变化
流态分析是研究弧底梯形短喉道量水槽水力特性的基本要素。为观测不同喉道长度、不同流量下量水槽段水面线沿程变化,选择对底弧半径为260的弧底梯形短喉道量水槽进行模拟研究,i=1/1 800、ε=0.61,四种体型喉长分别为0,0.25,0.5,1 m。图3为不同喉道长度量水槽过槽水流的水面线变化情况,由图3可见,量水槽上游水面水流均平稳,在量水槽进口收缩段(L=200~202.7 m)水面线开始缓慢降落,在出口扩散段前半段处水面线急剧下降,从喉口处开始有所不同,喉长a=0量水槽扩散段水流较其他3个湍急,水面曲率大,水面下降位置比其他量水槽靠近量水槽喉口,其他量水槽因喉道长度较其长给水面跌落以缓冲力,使水面跌落比较平缓。水流流经量水槽受到侧收缩而产生临界流,从而形成单一稳定的流量关系,此时通过上游水深即可得出过槽流量。

图3 不同喉道长度下量水槽过槽水流水面线Fig.3 The surface line of the flume under different throat lengths
图4为i=1/1 400、ε=0.61、a=1时,不同流量下弧底梯形短喉道量水槽水面线变化情况。由图可知,水面线变化均平缓,水深沿水流方向变化趋势与图3一致,且水面线随流量增大而上移。
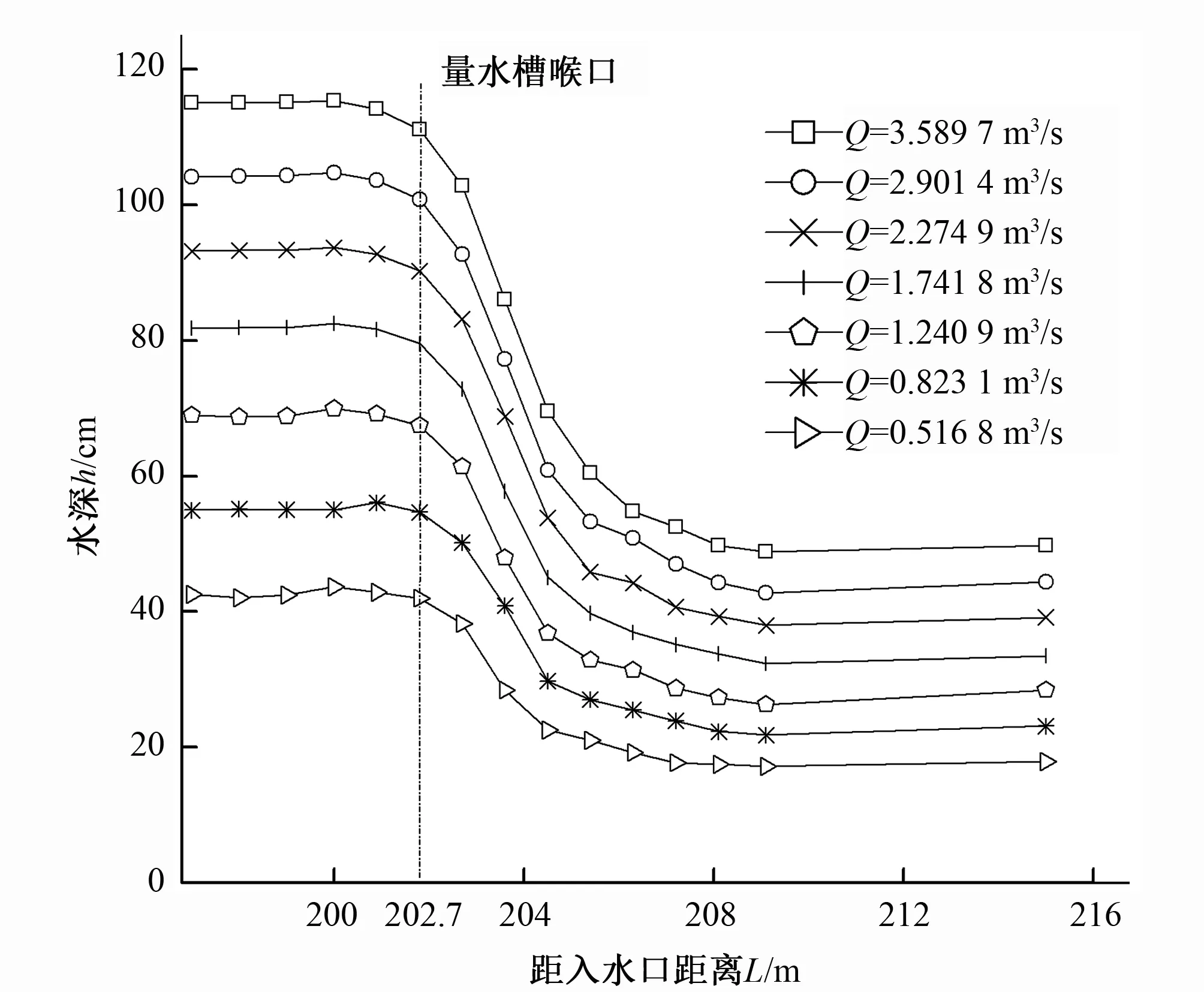
图4 不同流量下水面线变化Fig.4 Variation of surface line at different flow rate
3.3 弗劳德数变化及临界水深位置
3.3.1 不同情况下槽前弗劳德数变化
弗劳德数作为明渠水流流态判别的标准,在量水槽测流过程中是十分重要的。由图5可以看出,渠道上游水流平稳,Fr小于0.5,满足明渠测流规范要求。以ε=0.61,i=1/1 400为例,不同喉道长度下槽前弗劳德数变化见图5,a=1,i=1/1 400时不同收缩比情况下的槽前弗劳德数变化见图6。由图可得,随流量增大,弗劳德数呈先减小后增大趋势,总的来看,弗劳德数与喉道长度为负相关关系,即喉长越长,弗劳德数越小。随着收缩比减小,弗劳德数逐渐减小,同一收缩比情况下,弗劳德数呈先减小后增大的趋势。

图5 不同喉道长度下弗劳德数变化Fig.5 Variation of Froude number at different throat lengths

图6 不同收缩比下弗劳德数变化Fig.6 Variation of Froude number at different shrinkage ratios

图7 不同喉道长度沿程弗劳德数变化Fig.7 Variation of Froude number along different throat length
3.3.2 沿程弗劳德数变化及临界水深位置
佛劳德数Fr可以作为明渠水流流态判别的标准。Fr<1时,水流流态为缓流;Fr=1时,水流流态为临界流;Fr>1时,水流流态为急流。ε=0.65,i=1/1600时,量水槽在不同喉道长度情况下,沿程弗劳德数的变化情况见图7,由图可得,水流在量水槽入口至喉口收缩断面为缓流,Fr<1;在量水槽收缩段内,随着过流断面减小,流速逐渐增大,水面线开始下降,佛劳德数不断增大,水流流态仍为缓流;在量水槽出口扩散段内,水面线急剧下降,断面佛劳德数继续增大,当水面线下降到一定程度时形成临界流,对应的水深即为临界水深,此时Fr=1;由于惯性作用,水面线继续降低,流速不断增大,其大小和方向均发生变化,水流流态变为急流,此时Fr>1;在量水槽下游段,Fr值达到最大。可以看出,4条曲线Fr变化总体趋势一致。
为准确确定Fr=1即临界水深位置,将弗劳德数相关数据导入matlab中,对左图虚线框部分进行局部放大,用ginput进行点的确定和坐标的读取。李杰[14]所得巴歇尔量水槽临界水深断面在喉道段前5 cm内,肖苡辀[10]所得田间便携式短喉道量水槽临界水深在喉道段内。本文所选四种不同体型量水槽喉道末端x值分别为202.7,202.95,203.2,203.7,matlab导出四个交点从左至右分别为(203.601,1),(203.655 3,1),(203.785 3,1),(204.018 1,1),可以看出,随喉道长度的增加,临界水深位置后移,且临界水深断面发生在量水槽扩散段内,约为喉道段后30 cm左右。
3.4 水头损失分析
液体的黏滞性是产生水头损失的根本原因。弧底梯形短喉道量水槽过槽水流水头损失包括两部分,因与渠槽边壁摩擦产生的沿程水头损失和因侧收缩存在,渠道渐变段形状改变,水流结构急剧调整而造成的局部水头损失。对于喉口宽度小于22.86 m的短喉槽,水头损失较小,可以用上、下游测量水头差近似代替[15]。总水头:h=Z+P/γ+v2/2g,分别取弧底梯形短喉道量水槽收缩段首断面和扩散段末断面为上、下游水头控制断面,上下游水头差即为水头损失hw。
以ε=0.61,i=1/2 400为例,表3为弧底梯形短喉道量水槽在时不同喉道长度下水头损失的变化情况,由表4可知,收缩比一定时,随喉道长度增大,水头损失呈增大趋势。表4为喉长a=0.25,i=1/1 400情况下,不同收缩比所对应水头损失变化情况。由表可得,喉长一定时,随收缩比增大,水头损失呈减小趋势,这是因为收缩比越小,使得侧收缩越大边界条件变化急剧,局部水头损失变大;同一收缩比时,量水槽水头损失随着流量增大而减小,个别点小流量时误差较大,因为小流量下收缩比较大流量的收缩比小,导致小流量相对大流量水头损失要大。
3.5 公式以及模拟误差
试验模拟了3种弧底梯形短喉道量水槽不同流量工况下的水位流量关系,水位流量相关性较好,通过数据分析可知,流量与收缩比ε、上游水深h、喉道长度a有关。对流量数据进行回归分析,得到流量的经验公式如下:
a=1 mQ=1.086 5(εw)1.113 9h2.020 41
a=0.5 mQ=1.276 7(εw)0.902 2h2.005 5
a=0.25 mQ=1.348 5(εw)0.88h2.010 4
(6)

表3 不同喉道长度下水头损失变化Tab.3 Variation of head loss at different throat lengths

表4 不同收缩比下水头损失变化Tab.4 Variation of head loss at different shrinkage ratio
式中:Q为过流流量,m3/s;ε为量水槽收缩比;h为上游水深,m;W为喉口宽度,m;该公式测流范围为0.408 6~5.589 6 m3/s。
由公式(7)可以看出,流量受收缩比ε,喉道宽度W和上游水深h影响较大,且流量指数近似为2,可以尝试重新构造短喉槽自由出流流量公式,使过槽流量与上游水深的平方成正比,通过对不同喉道长度时的实验数据回归分析可得形如下的统一流量计算公式:
Q=A(εw)Bh2
(7)
式中:A=-0.353 8a+1.443 6,B=0.792 0ε0.329 6 a,a为喉道长度。
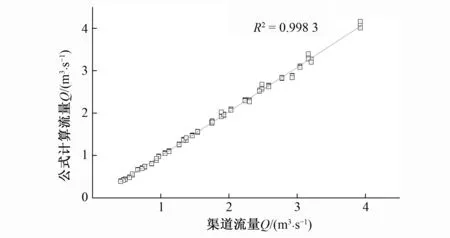
图8 渠道流量与计算流量对比结果Fig.8 Comparison results of channel flow and calculated flow
用公式(7)流量公式所得计算流量与渠道流量进行比较,图8表明二者具有较好的一致性,相关性可达0.998 3。表5为部分工况下渠道流量、模拟流量、公式计算流量对比结果,最大误差为6.98%,平均误差为1.74%,满足灌区测流要求。

表5 部分工况下渠道流量、模拟流量与公式计算流量的对比结果Tab.5 Results of channel flow, simulated flow and formula calculation under partial working conditions
4 结 语
本研究采用 RNGk-ε湍流模型和VOF方法相耦合,基于Fluent6.3大型流体力学计算软件对弧底梯形短喉道量水槽在上游渠长200 m,下游渠长50 m情况下进行数值模拟研究,研究结果如下:
(1)通过对9种弧底梯形短喉道量水槽和3种无喉道量水槽在不同工况下槽前和沿程弗劳德数变化情况进行分析,确定临界水深发生位置在量水槽扩散段,喉道段下游30 cm内。
(2)通过对弧底梯形短喉道量水槽水头损失分析得知,最大水头损失为总水头的5.98%,最小水头损失为总水头的1.09%,小于长喉道量水槽的13%,且比无喉道量水槽水流平稳,水面变化稳定性好,该理论为修建灌区新型量水槽提供了新思路。
(3)模拟流量与渠道流量误差除个别小流量点外均小于5%,二者吻合程度较好,说明模拟具有一定的可靠性。所建立的自由出流状态下弧底梯形短喉道量水槽的统一流量公式平均误差为2.43%,精度较高,简单可用,以期为后续其他量水槽测流公式的拟定提供参考。
□
[1] 严晓军. 我国灌区量水技术现状及发展趋势[J]. 中国科技信息,2010,(17):89-90.
[2] 郝晶晶,马孝义,王波雷,等. 灌区量水设备的研究应用现状与发展趋势[J]. 中国农村水利水电,2008,(4):39-41.
[3] 钟新铭,马孝义,王文娥,许坤鹏,樊琨.弧底梯形渠道无喉道量水槽水力特性的数值模拟[J].西北农林科技大学学报(自然科学版),2016,(4):218-224.
[4] 杨珮珮.弧底梯形无喉道量水槽的数值模拟与体型优化研究[D]. 陕西杨凌:西北农林科技大学,2016.
[5] Parshall RL. The Improved Venturi Flume[M]. USA: Colorado Experiment Station, Fort Collins, Coloado Agricultural College, 1928.
[6] Cone VM. The Venturi flume [J]. Journal of Agricultural Research, 1917, 9(4):116-129.
[7] Blaisdell F W. Results of Parshall Flume Tests[J]. Journal of Irrigation and Drainage Engineering, 1994,120(2):278-291.
[8] 李 杰, 吕宏兴, 胥维纤. 巴歇尔量水槽水流特性试验研究[J]. 节水灌溉,2009,(12): 45-47.
[9] 李香平, 杨兆选, 张 涛. 改进型帕歇尔水槽[J]. 天津大学学报, 2004,(5): 419-422.
[10] 肖苡辀,王文娥,胡笑涛. 基于FLOW_3D的田间便携式短喉槽水力性能数值模拟[J]. 农业工程学报,2016,32(3): 55-61.
[11] 潘志宝. 机翼形量水槽水力特性试验与数值模拟研究[D]. 陕西杨凌:西北农林科技大学, 2009.
[12] 张明亮,沈永明.RNGk-ε湍流模型在三维弯曲河流中的应用[J].水力发电学报,2007,(5):86-91.
[13] 钟新铭,马孝义,杨珮珮. 弧底梯形渠道无喉道量水槽水位流量关系数值模拟[J]. 水土保持研究,2016,(2):340-345.
[14] 李 杰.巴歇尔量水槽水力特性试验研究[D]. 陕西杨凌:西北农林科技大学,2010.
[15] 王长德. 量水技术与设施[M]. 北京: 中国水利水电出版社,2005.
