三角洲型感潮河口泥沙输移规律研究
2017-03-21王亚南郭维东李东斌
王亚南,郭维东,李东斌,王 颖,钱 彤
(1.沈阳农业大学 水利学院,沈阳 110866;2.河北省水利水电勘测设计院,天津 300250;3.阜新市凌河保护区管理局,辽宁 阜新 123000;4.朝阳市凌河保护区管理局,辽宁 朝阳 122000)
我国海岸线长达1.8万多km,河口及海岸交通便利、资源丰富[1]。河口港的扩建、河口三角洲的整治、河口建闸工程以及渔业和石油的开发等,均会导致严重的河口泥沙问题,因此对河口地区泥沙运动规律的研究具有重要的作用。国内外对河口泥沙数学模型的研究经历了一维、二维到三维的过程。郑国栋[2]建立了横向、纵向、垂向3个维向,分别分析了珠江三角洲的地貌变化, 张心凤[3]建立二维动边界非恒定潮流泥沙数学模型,对潮流泥沙冲淤情况进行了研究。三维泥沙数学模型由于模型结构复杂、计算工作量较大的因素发展较缓慢[4]。随着计算机技术的发展以及实际工程和研究的需要,简单的三维泥沙数学模型逐渐应用到计算中[5-8]。
根据河口平面形态将河口分为喇叭形、弯曲形、顺直形、三角洲形[9]。三角洲形河口平面形态较喇叭口型相似,是由顺直形和喇叭口形转化过而来,其最大特点就是在河口出口处形成河口三角洲。本文拟采用数值模拟方法,对三角洲型感潮河口在不同初始条件和边界条件下进行数值模拟。通过地形资料实现所研究河口地区的建模;选择数学模型,设定初始条件和边界条件,并采用实测资料验证模型的准确性,对三角洲型河口泥沙输移的规律进行了计算和分析。
1 基本控制方程
控制方程主要包括:连续方程、动量方程、输运方程、泥沙控制方程、地质演化方程。
(1)连续性方程:
(1)
(2)动量方程:
x方向上:
(2)
y方向上:
(3)

(3)输运方程如下:
(4)

(4)泥沙控制方程。
输沙公式如下:
qt=qb+qs
(5)
式中:qt为总输沙率;qs为悬移质输沙率;qb为推移质输沙率。
(6)
式中:T为时间;u为瞬时速度;c为瞬时悬沙浓度;D为瞬时水深;d为悬沙粒径。
(10)
式中:θc为泥沙启动的临界剪切应力;θ′为与底表面摩阻有关的无量纲剪切应力;p为一层内所有砂砾都启动的概率;s为泥沙的相对密度;d为泥沙粒径;ψ为横向长度尺度;Uf为一个波浪周期内的摩擦系数;μs为静摩擦系数(μs=tanφs,φs为休止角);θc,0为临界Shield系数;β为动摩阻参数。
(5)地形演化控制方程。河床变化率的计算采用泥沙连续方程:
(11)
式中:n为河床孔隙率;t为时间;Sx为x方向上推移质的总输沙率;Sy为y方向上推移质的输沙率;z为河床高程;x,y为水平笛卡尔坐标;ΔS为泥沙源汇项,对于平衡输沙,源汇项为0。
为研究地形的变化引入了地貌演化的计算公式:
(12)
式中:ΔtHD为时间步长;Znew为变化后的水位;Zold为变化前的水位。
2 研究方案及模型建立
2.1 三角洲型河口简介
三角洲型河口是在河口出口处形成河口三角洲。例如长江三角洲和珠江三角洲。随着河口外延及口门的淤堵,上游处水位不断被抬高,当水位高出两岸地面一定高度时,水流就会改道,从自然堤的薄弱处决口,开辟一条新通道,并在新的口门重演上述过程,在这个不断改道的过程中,形成了河口三角洲,三角洲型河口示意图如图1所示。

图1 三角洲型河口示意图 Fig.1 Sketch map of delta type Estuary
本次模型计算区域为河北省秦皇岛市洋河河口,采用2009年版的电子海图及地质勘查四队提供的2011年6月实测地形图,为方便计算,本文模拟典型三角洲型河口,河床纵比降为0。模型中水域面积合计14.39 km2,其中海域面积13.00 km2。感潮河口段长度2.2 km、河口平均宽度850 m。计算区域网格划分结果如图2所示。

图2 三角洲网格划分结果图Fig.2 The Result of Mesh Genetation in Yang River Estuary
2.2 研究方案
本次研究方案主要对不同流量、不同来沙中值粒径条件下的河口水位、流速及河底高程变化进行了模拟。方案如表1。
2.3 系数选取
水平涡黏系数估计公式如下:

表1 三角洲型河口模拟方案Tab.1 The Calculation scheme table of delta style
(13)
式中:E为涡黏系数;A为单元面积;u和v为流速在x和y方向的流速;C为系数,范围在0.094~0.3之间。
糙率系数的选取根据现有的实测资料以及大量实验总结出的经验值。本文选取的糙率值为0.032(m·s-1)。
2.4 模型验证
模型率定的计算区域上边界定在洋河大桥以下的橡胶坝下游断面,距洋河大桥60 m,河口宽度540 m,河口长度1.2 km。海域边界取在距河口1.9 km边界,水域总覆盖面积约6.25 km2,洋河河口水系图如图3所示。验证指标选为水位和流速,潮位数据及泥沙数据均来自秦皇岛矿产水文工程地质大队勘察报告,在模拟时段内,实测数据和模拟数据计算结果如图4、图5。
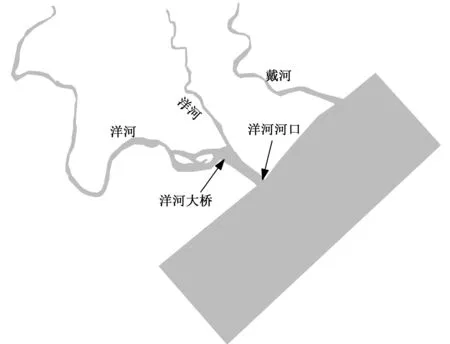
图3 洋河河口水系图Fig.3 The Yanghe River River Estuary map

图4 数值模拟与实测数据比较(水位)Fig.4 The contrast between numerical simulation and measured data(Water level)

图5 数值模拟与实测数据比较(流速)Fig.5 The Contrast Between Numerical Simulation and Measured Data(Current Speed)
为分析数值模拟的精度,分别计算其平均绝对误差(MAE)和均方根(RMSE)。计算结果见表2。

表2 水位与流速数值模拟评价效果Tab 2 Evaluation effect of numerical simulation:water level and current speed
以上计算精度均满足《海岸与河口潮流泥沙模拟技术规程》(JTS/T231-2-2010)中的精度要求。因此该模型在水动力模拟方面的结果是可信的。
3 计算结果分析
3.1 方案一结果分析
在相同控制流量Q1=500 m3/s、不同来沙中值粒径d50=0.1 mm、d50=0.2 mm及d50=0.3 mm条件下,计算A、B、C点的水位、流速及河床高程的变化趋势。
3.1.1 水位流速数值模拟
由图6、图7、图8可知,d50=0.1 mm工况的水位变化在模拟时段的前段时间波动较剧烈,在A、B点上,5 d后水位逐渐趋于平稳,A点水位范围为2.2~2.5 m,B点水位范围为1.6~2.4 m,在C点上,10 d后逐渐趋于平稳,水位范围为1.2~2.2 m;流速的变化趋势为:在A、B上波动较平稳,A点变化范围为0.6~0.7 m/s,B点变化范围为0.4~0.55 m/s;在C点,模拟时候的后半段流速明显增大,变化范围为0.2~0.6 m/s。流速波动趋势与水位波动趋势呈反向关系。d50=0.2 mm工况和d50=0.3 mm与d50=0.1 mm工况的水位变化趋势不一致,在同一时刻,d50=0.1 mm工况的瞬时流速大于其余两种工况。

图6 方案一A点水位、流速曲线Fig.6 The curve of A point water level and current speed in plan 1

图7 方案一B点水位、流速曲线Fig.7 The curve of B point water level and current speed in plan 1

图8 方案一C点下水位、流速曲线Fig.8 The curve of C point water level and current speed in plan 1
3.1.2 河床高程变化数值模拟
在A点,3种中值粒径工况下的河床高程呈现不同的特点,d50=0.1 mm工况曲线中可以看出在开始的1天内,河床高程增长迅速,6月16日之后保持平稳,在6月26日之后河床高程再次增长;d50=0.2 mm工况则以同一个河床增长率增长,波动不大。d50=0.3 mm工况下,河床高程变化较小,略有淤积,在6月26日之后略有下降。B点位于三角洲洲头,在三种中值粒径下保持河床高程增长,d50=0.1 mm工况河床变化最为剧烈,d50=0.3 mm工况则最为平缓。C点位于河口出口三角洲之后,其冲淤规律与A、B点不同,中值粒径为d50=0.2 mm及d50=0.3 mm工况存在冲刷,且d50=0.3 mm冲刷较严重。见图9-图11。

图9 方案一A点河床高程曲线Fig.9 The curve of A point bed level in plan 1
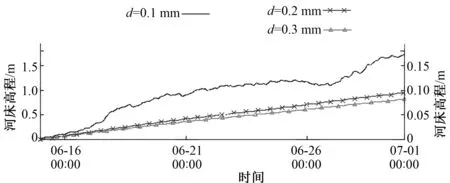
图10 方案一B点河床高程曲线Fig. 10 The curve of B point bed level in plan 1

图11 方案一C点河床高程曲线Fig.11 The curve of C point bed level in plan 1 注:图9-11中,横轴为模拟时间,左侧纵轴为Q=500 m3/s,d50=0.1mm工况下的河床高程;右侧纵轴则为Q=500 m3/s,d50=0.2 mm及d50=0.3 mm工况下的河床高程。
3.1.3 淤积部位数值模拟
在研究三角洲形河口的淤积部位的过程中,除了提取典型断面单点处的水力及泥沙要素外,还提取了平面二维的河床高程图,进而可以从整体上观察不同工况下的冲淤部位的规律。
图12-图14表示是Q=500 m3/s,d50=0.1 mm、d50=0.2 mm、d50=0.3 mm工况下,模拟进行了15 d以后的结果。从图12-图14可知,在三角洲型河口存在比较明显的冲淤区域,当上游来水经过河口三角洲时,三角洲洲头形成低流速区,这个区域中的水流掀沙能力很低,形成淤积区,Q=500 m3/s,d50=0.1 mm工况下淤积较严重,最大淤积厚度为1.2 m。河道断面分汊处造成冲刷,Q=500 m3/s,d50=0.2 mm工况下冲刷较剧烈,最大冲刷深度为0.06 m。水流从分汊河道流出后在三角洲尾部形成滞留区,流速降低产生淤积,Q=500 m3/s,d50=0.1 mm工况下,最大淤积厚度为1.2 m。

图12 Q=500 m3/s, d50=0.1 mm计算15 d后河底高程等值线图Fig.12 The curve of bed level isolines in the time 15 days with the model in Q=500 m3/s, d50=0.1 mm

图13 Q=500 m3/s, d50=0.2 mm计算15 d后河底高程等值线图Fig.13 The curve of bed level isolines in the time 15 days with the model in Q=500 m3/s, d50=0.2 mm

图14 Q=500 m3/s, d50=0.3 mm计算15 d后河底高程等值线图Fig.14 The curve of bed level isolines in the time 15 days with the model in Q=500 m3/s, d50=0.3 mm
3.2 方案二结果分析
在相同来沙中值粒径d50=0.16 mm,不同控制流量Q2=200 m3/s、Q3=10 m3/s条件下,模拟计算A、B、C点的水位、流速及河床高程的变化趋势。
3.2.1 水位流速数值模拟
图15表明,两种工况在流量不同、中值粒径不同情况下,同一时刻水位相差较小,整体变化的趋势与潮水位的变化趋势相同。
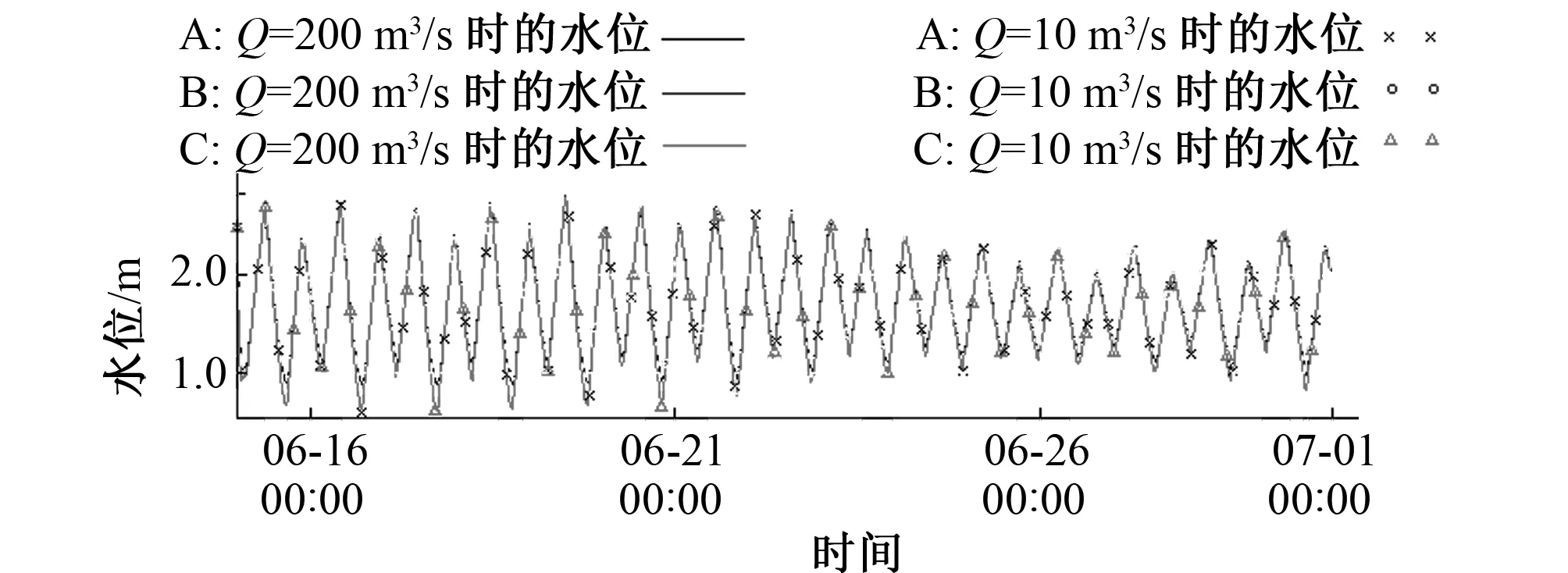
图15 方案二A、B、C点水位曲线Fig.15 The curve of ABC point water level in plan 2
从图16与图17可知,在三角洲型河口中流速变化较为有规律,接近正弦曲线。在同一时刻A点波动范围为0.14~0.34 m/s,B点波动范围为0.04~0.22 m/s,C点波动范围为0~0.14 m/s,A点流速最大,C点流速最小。由于流量的差异,Q=200 m3/s工况整体波动范围比Q=10 m3/s工况流速波动范围大。在Q=10 m3/s工况下,A、B、C流速曲线较为接近,与Q=200 m3/s工况相比较,波动没有明显规律。在同一时刻,B点流速最大,C点流速最小。

图16 Q2=200 m3/s, d50=0.16 mm ABC点流速曲线Fig.16 The curve of A、B、C point Current Speed in Q2=200 m3/s

图17 Q2=10 m3/s, d50=0.16 mm ABC点流速Fig.17 The curve of A、B、C point Current Speed in Q2=10 m3/s
3.2.2 河床高程变化数值模拟
为研究单点处的河床高程变化,提取了A、B、C三点在整个模拟时段内的河床高程值,图18表示的是在以上两种工况下三点的河床高程与时间的变化曲线。
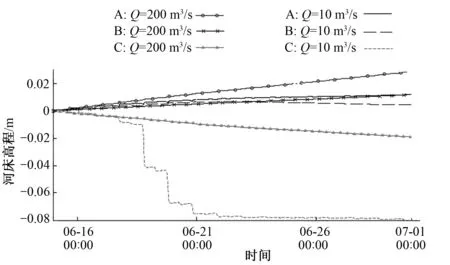
图18 方案二ABC点河床高程Fig.18 The curve of ABC point bed level in plan 2
由图18可知,在中值粒径相同情况下,流量、位置对冲淤规律有一定的影响。在Q=200 m3/s工况下A、B两点为淤积区域,且B点淤积程度较大,C点高程为负值,为冲刷区域。在Q=10 m3/s工况下,流量较前一种工况小,在三角洲挟沙量小,淤积程度较小。分汊流带来的泥沙在三角洲后滞留区的补给量较小,导致在枯水期C点的冲刷程度加大。
3.2.3 淤积部位数值模拟
为研究河口冲刷范围及规律,提取了在模拟开始15 d后对应的河口河床高程等值线图。图19与图20表示Q=200 m3/s及10 m3/s,d50=0.16 mm工况下的两个时间上的平面二维河床高程等值线图。
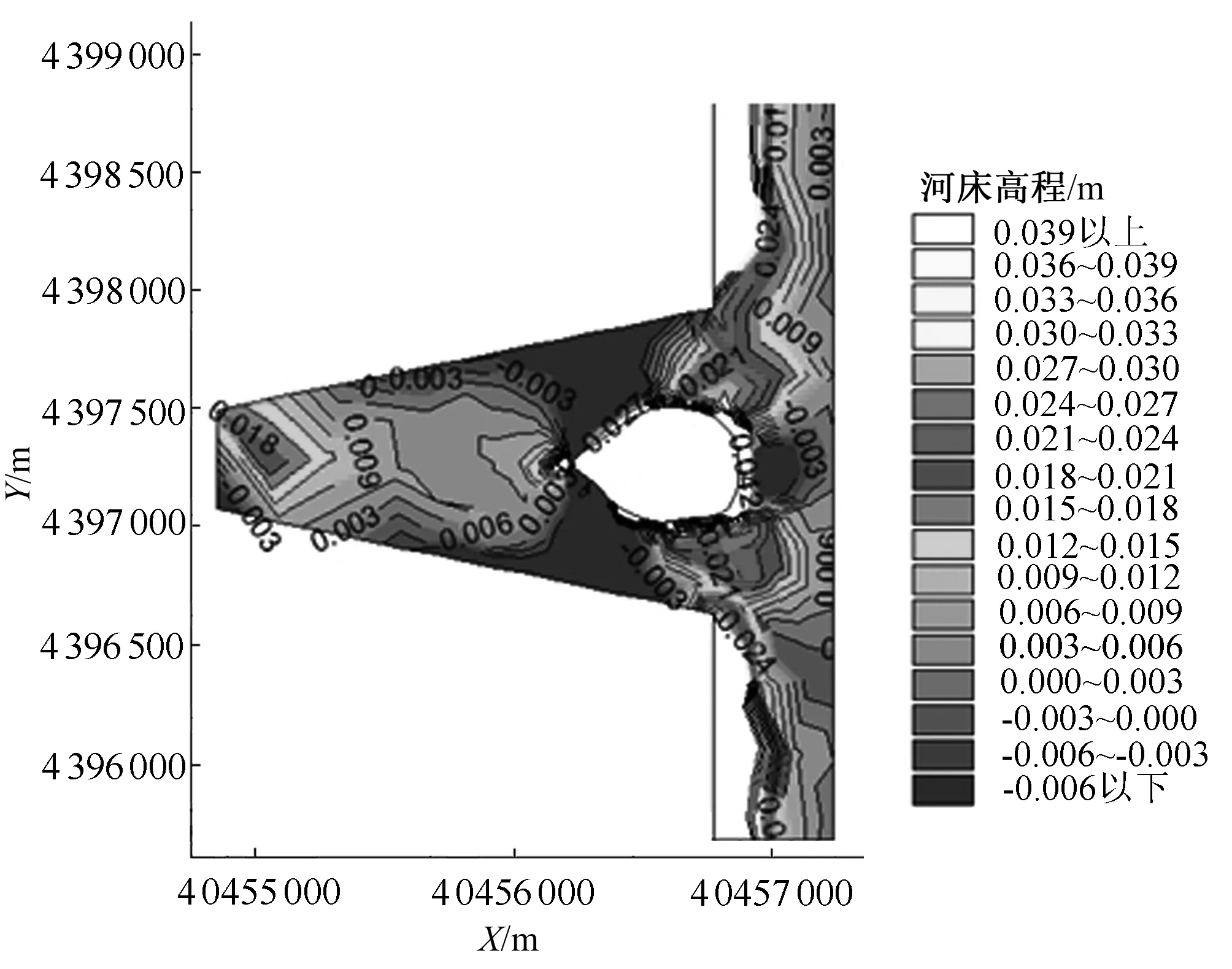
图19 Q=200 m3/s, d50=0.16 mm计算15 d后河底高程等值线图Fig.19 The curve of bed level isolines in the time 15 days in Q=200 m3/s

图20 Q=10 m3/s,d50=0.16mm计算15 d后河底高程等值线图Fig.20 The curve of bed level isolines in the time 15 days in Q=10 m3/s
从图19、图20可知,Q=200 m3/s与Q=10 m3/s工况下的冲淤结果是不同的,在中水期(Q=200 m3/s)河道是在径流和潮流共同作用下,在分汊河道和三角洲尾部正中形成冲刷区域。在洲头和三角洲尾部两端形成淤积区域。在枯水期潮流作用大于径流占主导地位,进水口至洲头区域河床高程存在很小的冲刷,冲刷深度在三角洲至外海区域受海流作用明显。
4 结 语
(1)丰水期不同泥沙中值粒径对河口水位的影响较小,潮水位对河口水位影响较大,起主导作用,但是河口三角洲的存在使得不同点的水位呈现差异。随着时间的变化,波动趋于稳定。在对应的流速曲线和水位曲线成反向关系。三角洲型河口也存在比较明显的冲淤区域,三角洲两侧形成冲刷区,三角洲洲头以及三角洲尾部形成淤积区。
(2)中水期和枯水期,河口水位的变化规律和丰水期是一致的。在中水期,流速变化较为有规律,接近正弦曲线。在同一时刻进口的瞬时流速最大,三角洲后点处流速最小。在枯水期,流速曲线波动范围较大,同一时刻三角洲头处瞬时流速最大,进水口瞬时流速最小。中值粒径相同时,流量及点位对冲淤规律有一定的影响。在中水期,三角洲两侧和三角洲尾部正中形成冲刷区域,在洲头和三角洲尾部两端形成淤积区域;在枯水期,进水口至洲头区域河床高程存在很小的冲刷,在三角洲至外海区域受海流作用明显形成冲刷区域,出口两端是淤积区。
□
[1] 李文丹. 复杂河口海岸地区水动力数值模拟研究[D]. 哈尔滨:哈尔滨工程大学,2008.
[2] 郑国栋,顾立忠,李虎成,等. 珠江三角洲河道地貌变化对网河水情影响研究[J]. 中国农村水利水电,2010,(7):33-36.
[3] 张心凤,李 越. 银湖湾A区围垦规划潮流泥沙数值模拟研究[J]. 中国农村水利水电,2014,(8):62-66,72.
[4] 邵宇阳. 近岸潮流和泥沙运动三维数值模拟[D]. 南京:河海大学,2005.
[5] 郭维东,田茹妍,李东斌,刘冰. 弯曲型感潮河口泥沙输移规律的数值模拟[J]. 人民黄河,2016,(4):1-6.
[6] 赵张益. 河口海岸三维水沙运动的间断有限元模型研究[D]. 天津:天津大学,2014.
[7] 王效远. 考虑波浪破碎影响的近岸三维泥沙数学模型[D]. 天津:天津大学,2009.
[8] 王崇浩,韦永康. 三维水动力泥沙输移模型及其在珠江口的应用[J]. 中国水利水电科学研究院学报,2006,(4):246-252.
[9] 熊绍隆,曾 剑. 潮汐河口分类指标与河床演变特征研究[J]. 水利学报,2008,(12):1 286-1 295.
