使用SCS模型在无历史实测径流资料流域计算场次洪水总量

王加虎，梁菊平，李 丽，吴 辰，罗嘉西，刘玉冰

(河海大学 水文水资源学院，南京 210098)

流域水文模型[1]是指根据流域上所发生的水文过程进行模拟并建立的数学模型。由美国农业部土壤保持局(USDA SCS)[2-4]提出的SCS-CN模型，因为其对输入数据量要求不高、模拟精度高而被许多国家和地区广泛应用，是目前流域水文模型中被应用较为广泛的模型。该模型结构简单，其中径流曲线数(CN)是其需要的唯一综合参数，因而在无资料地区得到了较多的应用。径流曲线数(CN)是用来反映降雨前流域下垫面特征的无量纲参数，与土壤类型、前期土壤湿度、土地利用以及坡度等因素有关[5]，因此确定CN值是SCS模型的重点研究内容。

目前，国内有很多学者利用SCS模型来估算流域径流量。然而，传统的用于确定CN值参数表[6,7]是根据美国各种下垫面情况开发制作的，而我国的气候条件、主要的土壤类型及土地利用情况与美国并不相同，很难找到适用于中国的对应数据集[8,9]。而其他的土地利用/覆盖数据集很多，但是因为不同数据集的数据源、分类和精度不尽相同，所以和SCS模型中的土地利用/覆盖分类不能一一对应，也就无法直接查表得出流域CN值来。

本文根据SCS模型中的土地利用/覆盖分类数据集对常用的UMD数据集(美国马里兰大学建设的全球土地覆盖数据集)进行逐个分析，确定两者之间的对应关系，以适应国内的需求。

1 模型计算原理

SCS-CN值法基于水平衡方程，有两个主要的假设。第一，实际地表径流量(Q)与总降雨量(P)的比例等于实际入渗量(F)与最大潜在滞留水量(S)的比例；第二,降雨初损量(Ia)正比于潜在最大滞留水量(S)，即Ia=λS。

水平衡方程：

P=Ia+F+Q

(1)

假设一，比例方程：

(2)

第二假设，Ia与S的关系：

Ia=λS

(3)

P、Q、S都是长度单位，初损系数λ是无量纲级。产流之前，一部分降雨将被截留、填补洼地面和下渗，这三部分损失的降雨总和，用初损Ia表示。假设一表述了，第一，不用考虑只有部分区域产流；第二，蓄满产流或在湿润的地方产流；第三，忽略了蓄满产流的统计关系。方程(1)和方程(2)合并起来得：

(4)

上述方程就是通常意义上的SCS-CN法，而且只有在P≥Ia的时候有效；P≤Ia时，Q=0。从适用的角度出发，λ一般取值0.2，于是上述方程变为：

(5)

这个是SCS-CN法广泛应用的方程形式。主要从日降雨数据计算地表产流，而且只有一个参数S。SCS-CN法的参数S，取决于土壤类型、土地利用类型、水文条件以及前期湿度条件(AMC)。λ经常也被认为是依赖于地质与气候条件的区域性参数。

由于S的变化范围可以是零到正无穷，无量纲的CN值，变化范围在0≤CN≤100：

(6)

2 用遥感数据确定流域CN值

流域的集水范围很容易确定，从手工圈画[10]到基于DEM的流域特征提取[11]，方法很多[12]。确定流域集水范围后，根据流域内的土地利用/覆盖数据和土壤类型数据，按照面积加权确定流域CN值。

2.1 土地利用/覆盖数据集

SCS模型中的土地利用/覆盖分类，在野外比较概括，只划分了林地、草地、牧场和耕地；在城市、居民区和道路部分划分比较细致，有5种共12个二级分类(见表1)，但是很难找到适用于中国的对应数据集。其他的土地利用/覆盖数据集很多，因为不同数据集的数据源、分类和精度不尽相同，所以和SCS模型中的土地利用/覆盖分类不能一一对应，也就无法直接查表得出流域CN值来。

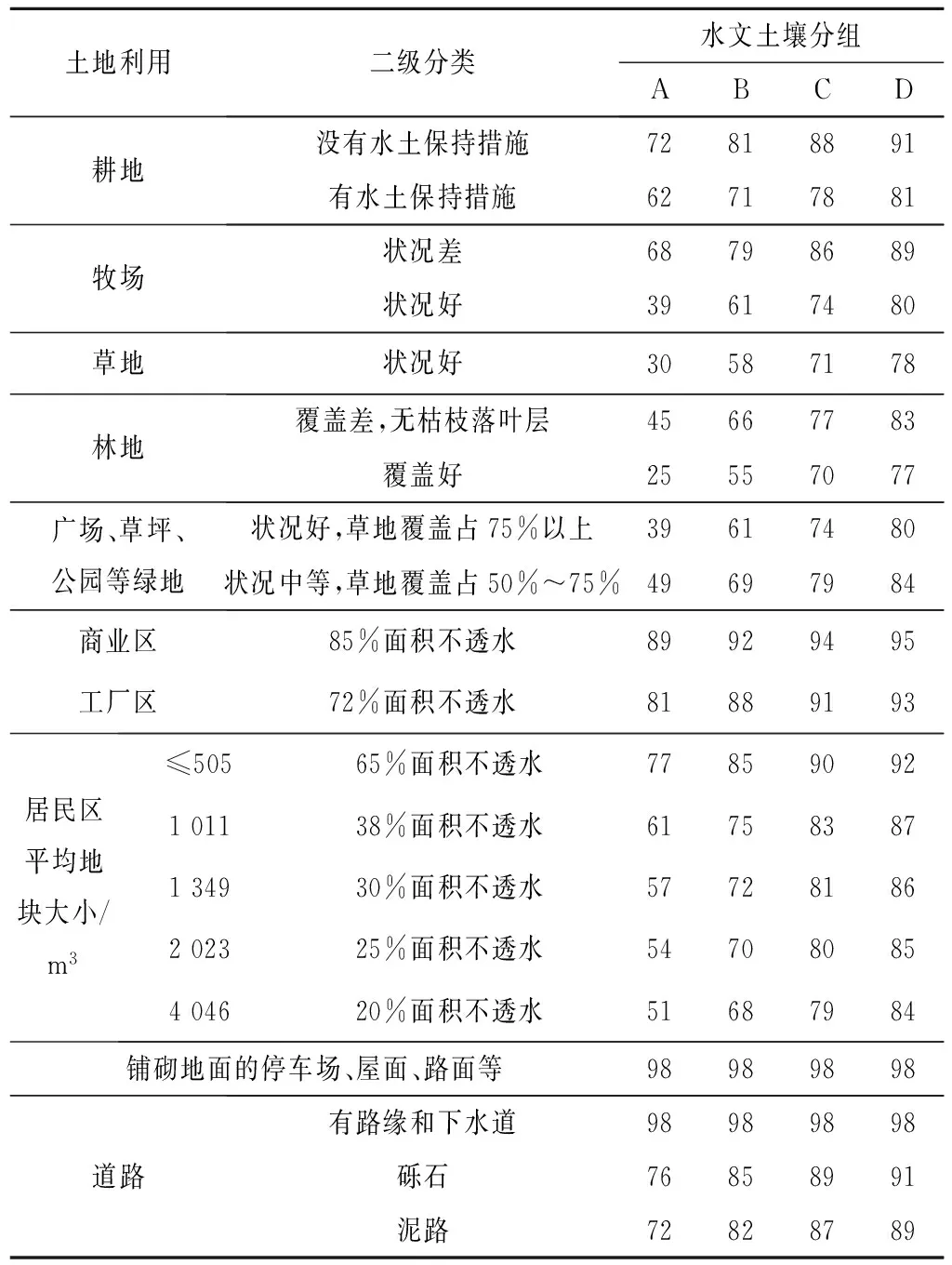
表1 SCS模型土地利用和径流曲线数Tab.1 Land utilization and curve numbers of SCS model

以常用的UMD数据集(美国马里兰大学建设的全球土地覆盖数据集)为例，其分类系统使用了简化的IGBP土地覆盖分类系统，共包括14个类别(见表2)；分类技术采用监督分类术，基于遥感数据，采用的是1992-1993年NDVI和AVHRR(1-5)波段数据组成41维的输入数据，分类精度较低，是以科学研究和环境监测为基本目的，应用目标是全球变化。

两个数据集之间没有明确的对应关系，只能按照描述、凭经验逐个分析UMD的数据并确定CN值，详见表2。

表2 UMD土地利用和径流曲线数Tab.2 Land utilization and curve numbers of UMD

2.2 土壤类型数据集

SCS的土壤类型划分考虑了美国农业部土壤质地分类，依据土壤的入渗率(裸土上长时间灌水后的测定值)将土壤划分为4组(见表3)，同样很难找到适用于中国的空间数据集。国际研究中比较常用的土地利用资料是USDA数据集，它按照美国农业部制定的土壤质地分类标准，其将土地利用分为12种，采用石块、砾石、沙粒、粉粒和黏粒五大类别，其中将粒径小于2 mm的颗粒视为土壤，其只考虑土壤颗粒粒级分布，没有考虑土壤的农业生产特性。这两个数据的土壤质地划分标准一致，可以根据输水率找出对应关系，见表4。

表3 SCS模型中的水文土壤分组Tab.3 Hydrological soil grouping in the SCS model

表4 USDA土壤类型分类Tab.4 Soil Classification of USDA

3 模型应用

本文以北京市北山下站[13]为例，检验上述CN值确定的适用性。该站流域面积135 km2、在30 sDEM中占据176个单元(见图1)。土壤类型全部为壤土；土地利用以稀树草原为主、共6种(见图2)。

图1 地形和站点分布Fig.1 Landform and distribution of stations

图2 土地利用分布情况Fig.2 Distribution situation of land utilization

3.1 查表确定流域综合CN值

本次研究以Hydro 1K 的地形流向、USDA的土壤类型和UMD的土地利用为例，获取各个典型流域的综合CN值，具体步骤如下：

根据流域出口水文站点的经纬度，提取出流域范围；

将土壤类型和土地利用数据叠加，确定对应的CN值。以北京市北山下流域为例，此步骤会得到如表5。

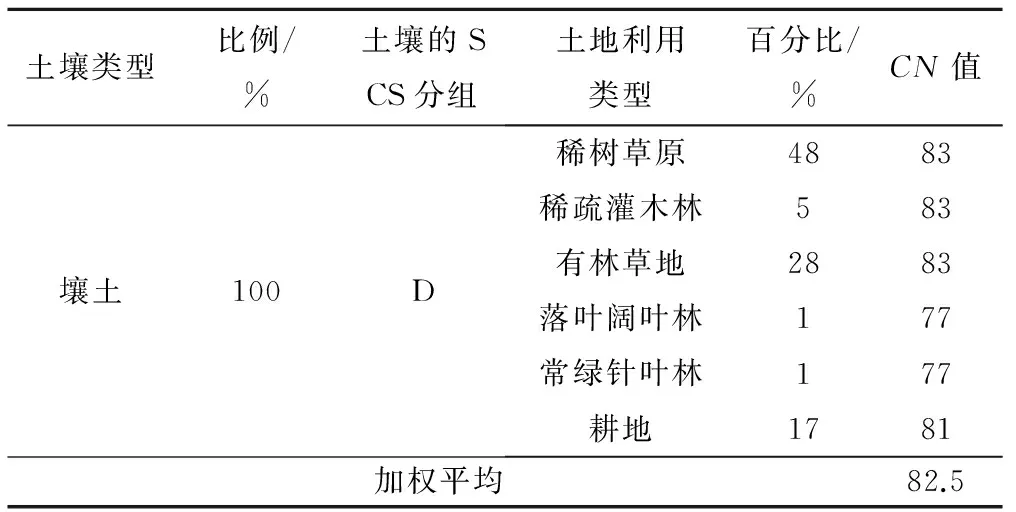
表5 北山下站流域综合CN值计算表Tab.5 Calculation table of integrated CN in theriver basin of Beishanxia station

根据前表5，确定该流域的CN值为82.5。

3.2 模型的应用

流域内有雨量站两个，北山下(权重67.6%)和沙厂水库(权重32.4%)，根据1981-1994年的降水和径流的资料匹配情况，通过人机交互挑选次洪一共17场，见图3。

图3 不同CN值计算场次洪水结果比较Fig.3 Comparisons of calculated flood results under different CN parameters

选用17场洪水反推CN，见表 6，流域平均为88.7。根据北山下站反推/查表的流域CN的修正系数为1.08。

用流域的查表和反推CN值分别计算17场次洪，平均的洪水总量误差分别为-39.6%和-10.8%。

表6 场次洪水不同CN值计算结果比较Tab.6 Comparisons of CN parameters in different flood event

使用上述反推CN值计算额外7场次洪水的逐时段产流过程、汇流模型计算后，峰现时刻合格率86%(标准是±1 h)、洪峰流量合格率57%(标准是±20%)，见表7。

表7 峰现时刻和洪峰流量验证Tab.7 Verification of peak time and peak flow

3.3 额外站应用与验证

本次选择北京锥石口站进行验证，此站只有锥石口一个雨量站。

根据降水和径流的资料匹配情况(见表 8)，一共挑选次洪16场。

表8 资料情况Tab.8 Information of Zhuishikou

流域内全部为壤土，植被以人工林地为主，夹杂少量农田和草地。 见图4、图5。

图4 土地利用分布Fig.4 Distribution stituation of land utilization

图5 地形和站点分布Fig.5 Landform and distribution of stations

查表CNb值为81.6，据此计算出11场洪水的总量误差在-89.4%到+6.4%之间、平均误差为-35.7%。北京市的校准系数取1.08，得到流域校准CN为88.1，计算出的11场洪水的平均误差为-5.0%。见表9，图6。

表9 场次洪水不同CN值计算结果比较Tab.9 Comparisons of CN parameters in different flood event

由北京锥石口站的验证结果可以看出来，根据UMD土地利用表和USDA数据集表确定的CN值用于场次洪水的模拟效果很好，计算出的11场洪水的平均误差为-5.0%，使用上述校准CN值计算额外5场次洪水的逐时段产流过程、汇流模型计算后，峰现时刻合格率100%(标准是±1 h)、洪峰流量合格率100%(标准是±20%)，见表10。

由表11可知将此方法确定的流域综合CN值用于无历史实测径流资料流域计算场次洪水总量是可行的。

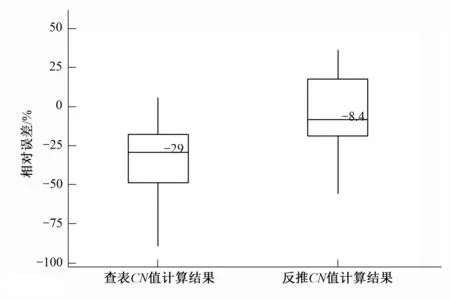
图6 不同CN值计算场次洪水结果比较Fig.6 Comparisons of calculated flood results under different CN parameters

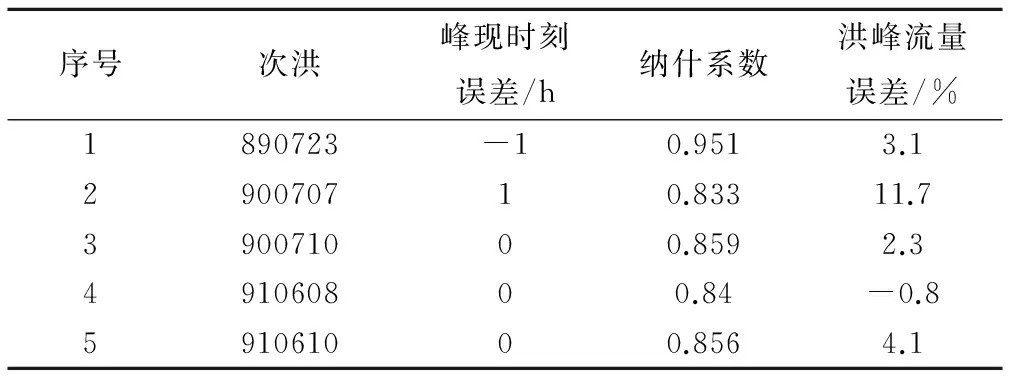
序号次洪峰现时刻误差/h纳什系数洪峰流量误差/%1890723-10.9513.1290070710.83311.7390071000.8592.3491060800.84-0.8591061000.8564.1

表11 在无资料站点计算总水量结果比较Tab.11 Compare the total amount of water at situation without historically actual runoff data

4 结 语

(1)本文随机选择了北京的锥石口站检验本文建立的方法体系。首先检验了流域校准系数对模拟结果的提高(见表11)，流域校准后的模拟结果都有了很大改善，包括平均误差减少以及次洪总量预测洪水的命中率提高、漏报率下降。

(2)其次检验了逐时段SCS产流加上流域汇流单位线在无资料地区的表现：模型较好的模拟出了峰现时刻和洪峰流量。北京锥石口利用改进SCS模型后其峰现时刻与洪峰总量模拟合格率均为100%。故本研究建立的方法体系经检验，可以用于无资料地区。

(3)利用同样的方法验证了北京柏崖厂站，同北京北山下站一样查表CN值计算出的洪水总量比实测值大，故证明了查表得到的CN值存在了系统偏差。可能的原因是：①建立UMD土地利用、USDA土壤类型与SCS-CN值对照表时，缺乏定量依据；②本研究选择的次洪大多是汛期的较大洪水，流域前期状况偏湿润，降雨产流率较大；查表CN值给出的是平均情况下的结果，所以计算结果偏小。

□

[1] 刘家福, 蒋卫国, 占文凤,等. SCS模型及其研究进展[J]. 水土保持研究, 2010,17(2):120-124.

[2] Soil Conservation Service(SCS)'Section 4,hydrology'.national engineering handbook[R].U.S.Department of Agriculture,Washington,D.C.1972:10.

[3] Soil Conservation Service(SCS).Hydroligy in National Engineering Handbook,Supplement A,Section 4,Chap.10, Soil Conservation Service[R].USDA,Washungton,1985:10.

[4] BOUGHTON W C A.Review of the USDA SCS curve number method[J].Australian Journal of Soil Research.1989,27(3):511-523.

[5] 符素华, 王向亮, 王红叶, 等. SCS-CN径流模型中CN值确定方法研究[J]. 干旱区地理, 2012,35(3):415-420.

[6] Soil Conservation Service Engineering Division.Urban hydrology for small watersheds.U.S.Department of Agriculture,Technical Release 55.1986.

[7] Neitsch S L, Arnold J G,kiniry J R, et al. Section 2:hydrology in soil and water assessment tool theoretical documentation[R]. Texas Water Resources Institute, College Station, Texas,2002:98.

[8] 符素华, 王红叶, 王向亮, 等. 北京地区径流曲线数模型中的径流曲线数[J]. 地理研究, 2013,32(5):797-807.

[9] 周翠宁, 任树梅, 闫美俊. 曲线数值法(SCS模型)在北京温榆河流域降雨-径流关系中的应用研究[J]. 农业工程学报, 2008,24(3):87-90.

[10] 王加虎, 郝振纯, 李 丽. 基于DEM和主干河网信息提取数字水系研究[J]. 河海大学学报(自然科学版), 2005,33(2):119-122.

[11] 李 丽, 郝振纯. 基于DEM的流域特征提取综述[J]. 地球科学进展, 2003,18(2):251-256.

[12] 宋晓猛, 张建云, 占车生, 等. 基于DEM的数字流域特征提取研究进展[J]. 地理科学进展, 2013,32(1):31-40.

[13] 王佳丽, 张人禾, 王迎春. 北京降水特征及北京市观象台降水资料代表性[J]. 应用气象学报, 2012,23(3):265-272.