基于MATLAB的FIR滤波器的仿真与设计

刘俊宏+杨晨光+张花普

摘要：在近代通讯系统的发展过程中，人们越来越优先选择通讯性能好、信息传递准确、传递效率高以及通讯工具无其他杂乱信号干扰的装置工具。因为许多装置会混有杂乱无章的其他信号，所以在信号处理过程中，数字滤波发挥着巨大的作用。除无效信号，大部分信号的分析处理都是经过滤波器滤来实现的，其中数字滤波器是最主要的一种信号处理方式，它是通过数值运算实现其滤波功能。比如：处理精度很高、运行相当稳定、数据处理非常灵活。本设计，详细介绍了不同类型的数字滤波技术和MATLAB语言环境下的编程技术，研究了各种滤波技术的现状和应用前景。具体介绍了数字滤波器：确定技术指标-逼近-性能分析-MATLAB仿真的设计方法，设计了FIR数字滤波器分析了他们的基本原理和设计方法，并在MATLAB软件中进行模拟仿真实验。

关键词：数字滤波器；FIR；MATLAB；窗函数

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2016）33-0200-03

数字滤波器是以数字信号为输入与输出方式，以一定的传输特性来传递信号的处理装置。它工作的基本原理是利用离散信号系统的特点改变输入信号序列的频率响应或者波形，阻止干扰信号的输出，从而输出所需要的信号。数字滤波器根据网络特性的结构特点可以分为有限长脉冲响应数字滤波器[FIR]和无限长脉冲响应数字滤波器[IIR]。[IIR]滤波器由在滤波过程中占的空间小，处理效率很高、处理精确，并且保留下一部分模拟滤波器的特点，因此实际应用中还是非常普遍的。对于[FIR]数字滤波器来说，它在滤波过程是以非递归的方式实现，滤波的过程和方式也不易改变，而且它在满足幅频响应特性的同时能够获得非常准确的频率特性，这种滤波器有利于对不同类型滤波器的频率特性进行数据分析与总结。在设计[FIR]型滤波器中，选用汉宁窗函数法设计带通滤波器，选用通带下线截止频率和上线截止频率分别为0.35和0.65，通过MATLAB仿真可以看出来，通带频率之外的其他频率信号削减幅度相当的大，最后使得在带通之外的信号在滤波的过程中过滤不在范围之内的信号，达到了选频滤波的目的。在高精度的信号分析与处理的过程中，比如传递数据、处理图像、音频信号的数字应用等领应用非常的广泛。

从真正的仿真结果可以看出来，MATLAB是一个运用起来非常简便、易于学习、运行速度快且便于操作的一种处理信号传输系统的软件，这个信息发展飞速的时代，数字滤波技术实用性很强，所以会应用在更多的领域，这是一个应用前景非常好的项目。

数字滤波器应用十分普遍，最主要应用在以下五个方面：

其一，可用于语音处理。在语音处理领域可以分为五个内容：A，用于分离多种语音信号；B，用于不同音色的辨别；C，用于共同声音合成；D，用于增强语音；E，用于语音编码等方面。

其二，可用于图像处理。数字滤波技术不但可以去干扰去噪音、恢复静止图像的完整、压缩图像数据，还能够识别图像并对X射线进行层析。与此同时，数字滤波器技术在雷达的检测、声纳的传递、超声波的传输与应用和红外信号的检测和应用方面也有相当重要应用。

其三，可用于电视。数字滤波技术及与之有关的技术，可以用于网络电视信号的发送和接受，是视频压缩技术和音频压缩技术的重要基础，目前应用领域非常广泛。

其四，可用于通信與生物医学信号。现代生活中，对于数字滤波技术的不断研究与数字滤波技术的快速发展，在现代通信技术领域内，数字滤波器在通信领域和生物医学信号处理应用的也相当广泛。通信领域有：多路复用，自适应信道均衡，数据压缩，信源编码和信道编码的调制等都相当多的领域采用了数字滤波技术；医学应用有：病人的身体检查，胎儿的自适应检查，心电图的检测与分析中，这些应用都非常重要。

其五，可用于雷达以及声纳。雷达和声纳都离不开数字滤波器及其技术，并且在军事与民生方面也发挥着重要的作用。

它的应用领域范围远远超过本文们的想象，比如军事上的目标导航、制导和战场的情况侦查；电力系统上的能源分布的情况规划和作为智能机器人系统自动检测；环境保护中可以作为智能系统对空气中的污染物和颗粒进行检测、自动监测各种环境的噪声干扰并进行报警处理；经济市场上可以根据往年的数据资料对股票走向进行预测、分析等。总之，数字滤波器应用的领域大大地超过一般人所能想象的范围。

1 数字滤波器的设计步骤

数字滤波器是以数字信号为输入和输出的信号处理装置系统，此信号系统具有一定的数据传输特性。滤波器可按照其冲击响应的时域特征分为无限长冲击响应（[IIR]）数字滤波器和有限长冲击响应（[FIR]）数字滤波器。在这两种数字滤波器在设计时可分为四个步骤：确定技术指标-逼近-性能分析-MATLAB的仿真四步。

1） 确定技术指标

在此次设计中根据实验所选择的滤波器的具体参数来决定数字滤波器的不同指标，从而根据频率响应给出频域的幅度和线性相位响应关系。幅度的指标分为幅度绝对指标和幅度相位指标两种，一般实验中幅度指标是最好的也是最受欢迎。线性相位通常在系统的通频带中进行实验所需要的响应，运用线性相位响应这个指标对滤波器进行基于MATLAB的设计有以下三个优点，首先算法采用的是及时数算法，没有其他的附属算法；其次，这个算法除了有固定数量的延迟之外，没有其他延迟失真的情况；最后，关于数量级的计算，计算量只需要计算长度为N的滤波器的一半。因此技术指标的确实是非常重要的。

2） 逼近

技术指标的选择好并确定了指标数值之后，在没有任何干扰情况下编写在MATLAB语言下的程序，在此基础下的对数字滤波器基本模型并进行MATLAB程序的编写从而进行模型的仿真与调试；然后根据具体情况与所给定的数值分析设计出数字滤波器的基本模型；最后让调试结果使其慢慢接近设定的理想指标数据。

3） 性能分析

由上述描述可得到一个差分活系统函数活脉冲响应滤波器，由此可得频率特性和相位特性的具体变化过程，用来检验设计结果的精准性。

4） MATLAB的仿真

利用MATLAB软件的Simulink系统进行仿真，通过滤波器仿真显示来观察最终结果并进行仿真结果分析，从而优化数据得到最好设计方案。利用MATLAB软件设计的[FIR]数字滤波器，简单的程序编写不但可以节省许多编程时间，提高了编写程序的效率，而且能够依照不同的条件不断改变参数，从而观察不同数值下的滤波情况并且显示出来，直观的看到不同的地方，使得滤波器达到最优效果。

2 [FIR]数字滤波器的步骤及设计方法

2.1 [FIR]数字滤波器的设计步骤

此实验选用汉宁窗函数的方法来设计FIR数字滤波器并在MATLAB软件上进行仿真。汉宁窗函数的设计步骤如下：

1）确定参数的关系

（1）根据已知的频率参数，来确定最理想情况下的滤波器的频率响应[HdejΩ]；

（2）根据已知数值来确定该滤波器的单位取样响应为[hdn]，其表达式为：

2）选择窗函数[wn]和窗长度[N]

根据设计的指标要求对滤波器的幅度和过渡带宽情况，首先确定阻带的衰减范围，再在这个范围内选择主瓣最窄的窗函数与窗长度[N]，最后计算滤波器的单位取样响应[hn]，表达式关系为：

3）检验函数关系是否正确，并对结果进行分析探索

[hn]的频率响应[Hejω]与[Hdejω]是否满足：

若所得数据满足上述关系，则说明参数比较合适，根据[hn]画出结构图；若不满足，再对第2、3步进行循环计算，不断探索。

2.2 [FIR]数字滤波器的设计方法

[FIR]数字滤波器的设计问题本质是找到题目中要求的脉冲响应常熟和序列的转移问题；[FIR]数字滤波器设计的方法可以分为以下几种：利用采样所得的具体频率来设计、利用示波器将窗函数显示出来的方法进行设计和等波纹最佳值逼近的设计方法等；将[FIR]滤波器的基本结构可形象描述为一个分节的延时线，使每一个的输出值进行加权并累加，将所得结果通过滤波器输出[1]。[FIR]数字滤波器的设计选用窗函数法，窗函数法的设计方法是通过一种用设置的宽度函数截取无限长脉冲响应序列从而获取有限长脉冲响应序列波形的过程。当用一个有限长波形序列[hn]来代替理想情况下没有任何干扰的时候滤波器的单位取样响应[hdn]时，必定产生一些误差，这种误差被称为吉布斯效应。这也可称为截断效应：因为这是将所需的单位脉冲[hdn]直接截下来，这会造成通带和阻带内有波动进而对其造成一定干扰[2]。

窗函数法又叫傅里叶级数法，随着傅里叶级数的项数越多，所得到的结果误差就会越小。但也不是项数越多就越好，随着项数的不断增加，就会使得所需要的成本和储存体积变大，所以本文在满足题目要求条件的基础上尽量减少有限长单位脉冲响应序列[hn]的长度。在现实的实验或者实践里，如果需要得到单位滤波，我们先对参数进行设置，用[N]表示滤波器阶数，[Wn]为窗函数表达式，根据滤波器性能与技术指标所设定的参数按照具体数值进行单位取样。该设计的主要思路是利用频率响应的特点来确定有限长单位脉冲响应[hn]的系数向量，将没有干扰情况下的脉冲响应[hdn]与窗函数[wdn]相乘得到有限長脉冲响应序列[hn]的方法，即[hn=hdn.Wn]。

选用窗函数法设计的条件是：第一，通带要窄；第二，尽量减小阻带内的波动范围来抑制阻带内衰减幅度作用；在进行实际操作时，窗函数可分为：矩形窗、三角形窗、汉宁窗、布莱克曼窗和凯塞窗五种[3]。图1是以上几种窗函数的参数值，如下：

3 [FIR]数字滤波器的MATLAB设计实例

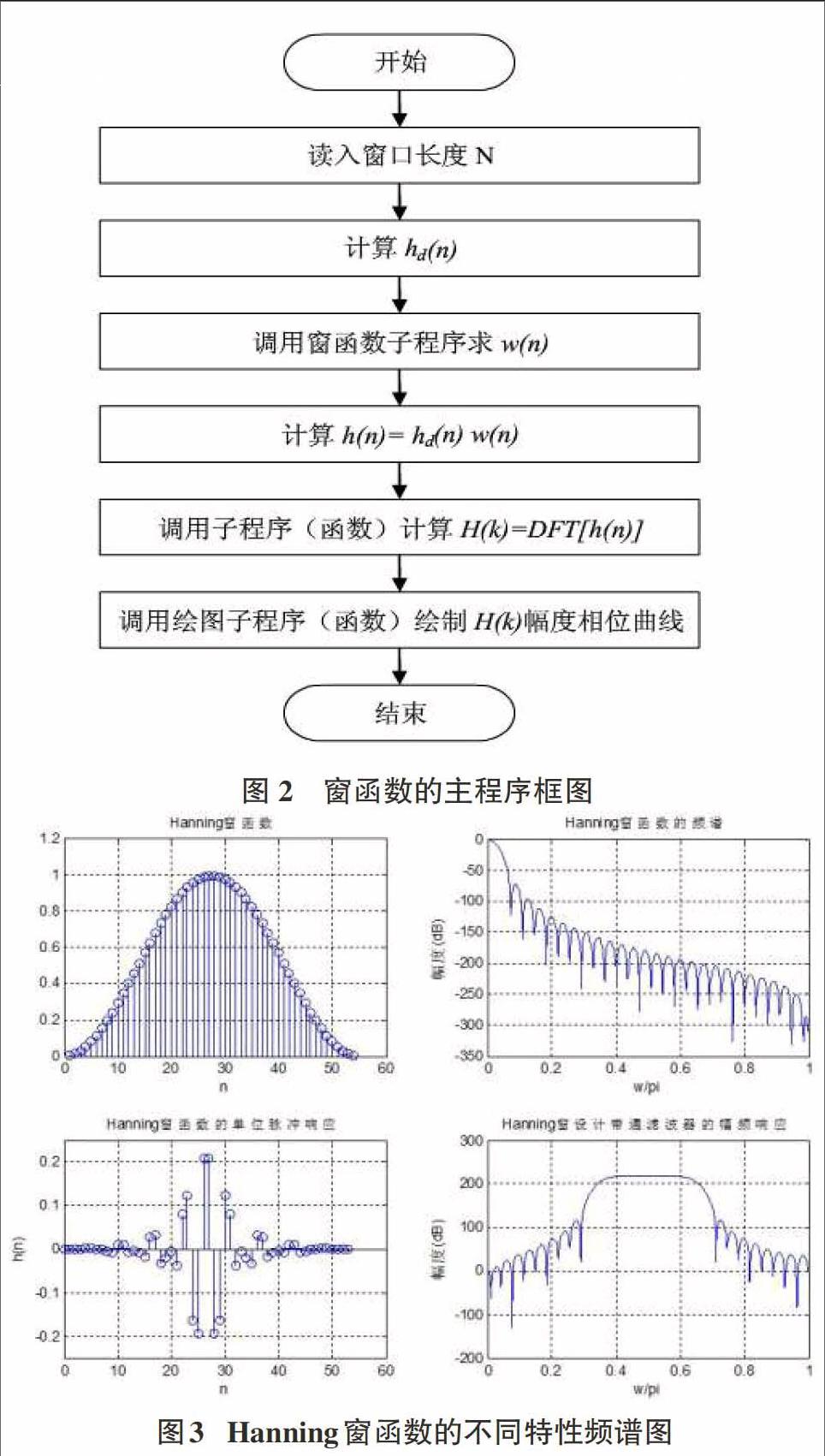
利用MATLAB设计窗函数的主程序框图可以表示如下图2：

在用窗函数法设计[FIR]数字滤波器的方法有很多种，经过考虑选择汉宁窗为例，首先根据具体情况设置各个参数值：低端通带截止频率设为[w1p=0.35π]，低端阻带截止频率设为[ω=0.2π]，高端阻带截止频率设为[whs=0.8π]，高端通带截止频率设为[whp=0.65π]，通带最大衰减设为[Rp=1dB]，阻带最小衰减设为[Rs=40dB]，通过MATLAB编写程序，可得该汉宁窗的幅频特性曲线如图3：

4 数字滤波器的仿真结果分析

上述的设计过程叙述了有限长单位冲激响应数字滤波器（[FIR]数字滤波器）的原理，利用窗函数的设计方法对[FIR]数字滤波器进行了具体的设计与研究。利用窗函数设计[FIR]型数字滤波器时，本文选用汉宁窗进行设计与MATLAB的仿真设，汉宁窗的上线截止频率和下线截止频率分别为0.65[π]和0.35[π]，但是因为通带频率外的信号幅度衰减很大，因此滤波器能够对通带内的波形进行滤除，从而达到过滤通带之外波形的效果。利用MATLAB语言，根据不同情况改变参数来设计[FIR]数字滤波器，这种方法不但简单方便，最主要的是节省时间，便于观察和记录，还可以随时改变不同的参数，从而更直观的去研究各个滤波器的显示结果。因为传统数字滤波器的设计方法非常复杂，运算所得数据庞大，结果表现的也不直观，所以此次设计选择利用MATLAB语言设计一个更为优化的设计方案，对传统的数字滤波器进行改良，利用它强大的科学计算系统和图形显示的特点来去掉传统数字滤波器的缺点，实现对数据计算量的简化、提高了精度、使结果更直观表现出来等优点。

参考文献：

[1] 郭中华，董涌，房卫东，等.基于MATLAB的FIR数字滤波器设计与仿真[J].宁夏大学物理电气信息学院学报，2004，3.

[2] 黎民红.利用MATLAB和窗函数法设计FIR数字滤波器[J].华南大学学报，2007，9.

[3] 徐欢，胡津津，袁媛.基于 MATLAB的FIR数字滤波器的窗函数法设计与仿真[J].通化师范学院学报（自然科学版），2013，4.