基于水平集的纳米颗粒分割方法
2017-03-21吴玥陈志强张澍寰张芳
吴玥+陈志强+张澍寰+张芳


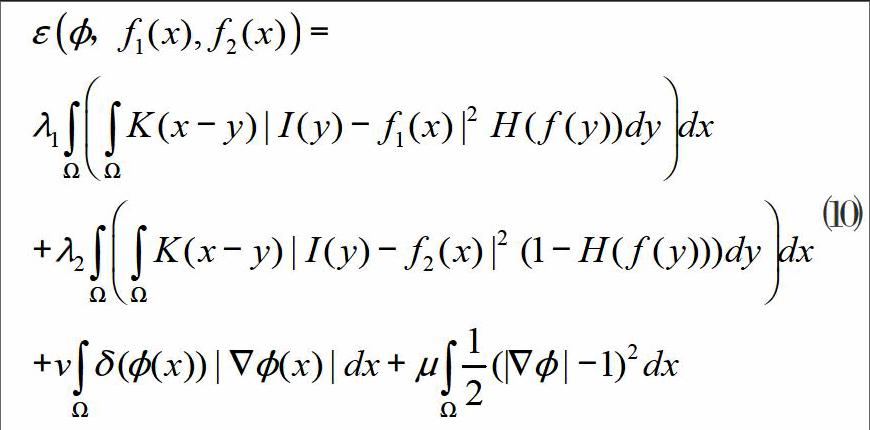
摘 要: 纳米颗粒尺寸测量技术对分析材料性能至关重要,而颗粒分割对纳米颗粒的质量评价有重要的意义。基于水平集图像分割方法对纳米颗粒进行分割。首先,利用偏微分方程对纳米颗粒图像进行预处理,针对不同的纳米图像设计合适的滤波方案。在此基础上,基于水平集图像分割算法分割纳米颗粒,分析了三种水平集模型对纳米颗粒的分割性能。实验结果表明,采用RSF水平集分割模型对灰度不均且具有弱边缘的纳米颗粒具有很好的分割效果。
关键词: 纳米颗粒; 水平集图像分割; 偏微分方程滤波; RSF分割模型
中图分类号:TP391 文献标志码:A 文章编号:1006-8228(2017)03-01-05
Abstract: Size measurement technique of nanoparticles is critical to the analysis of material properties. Particle segmentation is very important for the quality evaluation of nanoparticles. Nanoparticles are segmented with the level set image segmentation method in this article. Firstly, partial differential equation is used for preprocessing of nanoparticles image, and the proper filtering methods are designed depending on the type of nanoparticles. On this basis, nanoparticles are segmented with the level set image segmentation method. The segmentation performance of three level set models is analyzed for nanoparticles. Based on the experimental results, RSF (Region Scalable Fitting) segmentation model is adopted, which can overcome the difficulties such as uneven gray-level and weak edge of nanoparticles.
Key words: nanoparticles; level set image segmentation; partial differential equation filtering; RSF segmentation model
0 引言
納米技术广泛应用于催化科学、医学药物、新材料、电力工业和复合材料等产业,在整个高科技领域有着重要的地位[1]。由于纳米材料的很多特性都与其颗粒粒径的大小、形态等微观结构有着重要的关系,所以纳米材料微观结构的表征对认识纳米材料的特性、寻求纳米材料的应用领域、推动纳米材料的发展有着重要的作用。
基于图像处理技术对纳米颗粒图像进行处理和分析,是纳米颗粒尺寸测量的重要方法,其中颗粒个体分割是颗粒尺寸测量的关键步骤。水平集图像分割方法是把边缘演化曲线隐含地表示为一个更高维函数的零水平集,水平集函数在偏微分方程的控制下进行演化,直到零水平集演化到图像的目标边界为止。Li等人[2]提出了DRLSE模型,Chan和Vese[3]提出了CV模型,但这两个分割模型对具有弱边缘目标的图像分割效果并不理想。Li等人[4-5]后来提出局部区域拟合(Region Scalable Fitting, RSF)模型,将局部区域信息嵌入到区域型变分水平集中,用来驱动曲线的演化,获得了良好的分割效果。本文借助水平集图像分割方法实现纳米颗粒的准确分割。
本文针对透射电子显微镜下的球形纳米颗粒、棒状纳米颗粒和柱状纳米颗粒的分割问题进行研究,为后续对纳米颗粒的尺寸测量和表征提供依据。
1 图像预处理
由于TEM拍摄的纳米颗粒图像包含许多噪声,因此需要先进行滤波处理。由于纳米颗粒图像还具有弱边缘特性,因此在滤波的同时还要防止边缘模糊。为此本文采用偏微分方程滤波方法对纳米颗粒图像进行滤波,在去除噪声的同时很好的保护了颗粒边缘。常规的几种偏微分方程模型有热传导模型、PM模型、平均曲率流模型和选择退化扩散模型。我们将这几种偏微分方程滤波方法与高斯滤波方法进行对比。
图1是对柱状纳米颗粒进行滤波的结果,图1(b)为采用窗口大小为11×11、方差为2的高斯滤波器得到的滤波结果,可以看出滤波后颗粒边缘变模糊。由此可知HCE模型在平滑噪声的同时也模糊了边缘;PM模型滤波结果中在颗粒边缘处出现了锯齿现象,这是该模型在图像边缘处采取很小的扩散速率导致的不平滑现象;平均曲率流模型对边缘的保护情况较好,但颗粒外形的拐角处损失较多;相比而言选择退化扩散模型更能突出颗粒的弱边缘信息,是最佳的滤波方案。
由于颗粒制备的工艺不同,棒状纳米颗粒和球形纳米颗粒的透射电镜图没有柱状纳米颗粒的弱边缘特点,但是其噪声比柱状纳米颗粒的噪声更强,所以采用将平均曲率流模型和PM模型的滤波结果进行像素级相乘的策略,可以很好的去除棒状纳米颗粒的噪声,同时也能保留颗粒边缘。
经实验证明,对柱状纳米颗粒选择退化扩散模型具有较好的平滑效果且能保留颗粒的弱边缘;而对棒状和球形而言,选用PM模型和平均曲率流模型的滤波结果进行像素级相乘所得的平滑效果好,为后续颗粒分割奠定基础。
2 基于水平集的图像分割方法
水平集方法的基本思想是将图像域Ω中的闭合曲线C隐含的表达为三维连续函数曲面的一个具有相同函数值的同值曲线,通常称为水平集函数,称为零水平集。这样二维曲线演化就转化为高维函数曲面的演化,而随时间变化的曲线位置由高维函数的零水平集表征。本文主要介绍三种常用的水平集分割模型。
2.1 DRLSE模型
DRLSE模型是基于图像边缘的水平集模型,能有效地解决水平集基本理论中水平集函数需重新初始化的问题。但是DRLSE模型对初始化位置敏感,初始轮廓必须全部在目标物体的内部或外部,才能得到很好的分割结果。此外,该模型对于具有模糊边缘的图像分割不准确。
2.2 CV模型
假设任意封闭曲线C将图像I分成了外部区域Ωext和内部区域Ωint两部分,则水平集能量泛函表示为:
CV模型是利用图像全局信息来引导曲线演化,将轮廓内外的灰度值近似为一个常数模型,对于任意的初始化位置,最终都能够获得目标物体分割结果,因此CV模型有效地解决了对初始化位置敏感的问题,能有效地克服模糊边缘对分割结果的影响。但是该模型对于亮度不均匀的图像或者具有复杂目标的图像无法得到准确的分割结果。
2.3 RSF模型
RSF模型(基于区域扩展的水平集模型)通过引入局部二值拟合能量函数有效克服了CV模型的缺点。
设定义域为Ω的图像I:Ω→R是灰度图像,一个封闭的轮廓C将图像域Ω分为两个部分:内部区域Ω1和外部区域Ω2,假设在图像上每个点x∈Ω中有一个半径为ρ的圆形邻域,那么在每个点的邻域内,局部强度拟合能量泛函定义为:
其中,λ1和λ2为正数,f1(x)和f2(x)是在区域Ω1和Ω2中的点x的拟合图像强度的两个函数值,K(x-y)是核函数[7]。
根据水平集原理,轮廓C可以用水平集函数的零水平集表示,那么基于水平集的局部扩展拟合能量泛函表示为:
为了约束零水平集曲线,在以上拟合能量函数的基础上,加入轮廓C的长度项;为了使水平集函数稳定的进行演化,防止曲线出现畸变,加入正则化项,该函数项可以用来确保水平集函数在演化时始终近似为一个符号距离函数,避免的重新初始化过程。
綜上所述,最终的基于水平集的局部扩展拟合能量泛函为:
RSF模型主要在局部区域进行拟合,因此对边缘模糊、强度不均匀的图像能够给出很好的分割结果。
2.4 基于水平集的纳米颗粒分割
由于透射电镜采集的图像中,部分颗粒的边缘很弱且整体亮度不均。为准确定位边缘,本文应用RSF水平集分割模型,该模型对于弱边缘的颗粒有较好的分割效果。为了证明此模型的有效性,将结果与CV模型和DRLSE模型的分割结果进行对比。
在纳米颗粒分割实验中,设定最大迭代次数为500次。DRLSE模型效果如图4(a-1)所示,其中的参数为:Dirac函数参数ε=1.5,时间步长Δt=0.1,内部能量系数μ=0.2,曲线长度系数λ=5,面积系数ν=3。CV模型效果如图4(b-1)所示,其中的参数为:Dirac函数参数ε=1,时间步长Δt=0.1,曲线长度系数μ=0.001×255×255,内外能量系数λ1=1,λ2=3,曲线包含面积系数ν=0。RSF模型效果如图4(c-1)所示,其中的参数为:Dirac函数参数ε=1,时间步长Δt=0.1,曲线长度系数μ=1,内外能量系数λ1=1,λ2=5,曲线包含面积系数ν=0.004×255×255。
对于柱状纳米颗粒,DRLSE模型的分割结果中颗粒边界并不能完全分开,这是由于DRLSE模型中依靠边缘停止函数,容易陷入局部极小值,不能停在真正的边缘处,如局部放大图4(a-2)所示。在CV模型的结果中,由于颗粒的亮度不均且CV模型利用了图像的全局信息驱使曲线的演化,使曲线停在灰度值较小的颗粒内部如图4(b-2)所示。图4(c-2)是RSF模型分割结果的局部放大图,此模型利用图像的局部信息,即使是颗粒的弱边缘部分也能准确得到颗粒的边缘。
对于棒状纳米颗粒,DRLSE模型的分割结果如图5(a-1)所示,当颗粒灰度值和背景接近或者出现弱边缘情况,DRLSE模型并不能精确定位到纳米颗粒的真正边缘处,在图5(a-2)中圆形颗粒的右下部分没有定位准确。在CV模型的结果中如图5(b-1)所示,边界曲线停在了灰度值较小的颗粒内部,在局部放大图5(b-2)中的圆形颗粒同样未定位到颗粒的边界。图5(c-1)、(c-2)中RSF模型在弱边缘部分也能实现精确定位。
对于球状纳米颗粒,在图6(a-1)和(a-2)中,DRLSE陷入局部极小值,出现了颗粒粘连现象。CV模型对于图6(b-2)所示的颗粒边缘定位不准,边界曲线误定位到颗粒内部。RSF模型的边缘定位结果如图6(c-1)和(c-2)所示定位精确。
3 结束语
在对纳米颗粒图像处理的过程中,颗粒分割的结果对接下来的测量和统计分析的精度都有很大的影响。实验结果表明,对柱状纳米颗粒选择退化扩散模型具有较好的平滑效果且能保留颗粒的弱边缘;而对棒状和球形而言,选用PM模型和平均曲率流模型的滤波结果进行像素级相乘所得的平滑效果好。最后采用RSF水平集分割模型对纳米颗粒进行分割,这样可有效地克服弱边缘和光照不均对纳米颗粒分割带来的影响,从而为后续颗粒测量奠定良好的基础。但是由于纳米颗粒的形态种类繁多,本文只是针对柱状、棒状和球形单晶纳米颗粒进行测量,具有一定的局限性,对此还需要进一步完善和提高。
参考文献(References):
[1] C.E. Fowler, D. Khushalani, B. Lebeau, et al. NanoscaleMaterials with Mesostructured Interiors[J]. Advanced Materials,2001.13(9):649-652
[2] C.M. Li, C.Y. Xu, C.F. Cui, et al. Level set evolutionwithout re-initialization: a new variational formulation [C].Conference on Computer Vision and Pattern Recognition, San Diego,2005.1:430-436
[3] T. Chan, L. Vese. Active contours without edges[J]. IEEETransactions on Image Processing,2001.10(2):266-277
[4] C.M. Li, C.Y. Kao, J.C. Gore, et al. Implicit activecontours driven by local binary fittingenergy[C]. IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis,2007:339-345
[5] C.M. Li, C.Y. Kao, J.C. Gore, et al. Minimization ofregion-scalable fitting energy for image segmentation[J]. IEEE Transactions on Image Processing,2008.17(10):1940-1949
[6] C.M. Li, C.Y. Xu, C.F. Gui, et al. Distance regularized levelset evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing,2010.19(12):3243-3254
[7] C.M. Li, C.Y. Kao, J.C. Gore, et al. Implicit activcontours driven by local binary fittingenergy [C]. IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis,2007:339-345
