RSA数据加密算法分析与改进

孙赫+李少波

摘要：针对制造物联中数据的安全快速交换问题，该文提出了一种RSA的算法改进方案。RSA算法的核心是模幂运算，保证算法的可靠性。但是由于算法的复杂性导致运行速度慢。该文提出多素数及加速幂乘运算改进算法，并通过一种计算架构（CUDA）实现算法，结果表明，改进算法的效率更高。

关键词：RSA算法；CUDA； 算法改进；模幂运算

中图分类号：TP309.7 文献标识码：A 文章编号：1009-3044（2016）33-0045-04

Abstract： The problem of rapid exchange for manufacturing complex contact data security， this paper proposes a RSA algorithm improvement scheme. The core of the RSA algorithm is modular power algorithm， which ensures the reliability of the algorithm. However， due to the complexity of the algorithm， the running speed is slow. In this paper， we put forward a new algorithm to improve the multi prime and accelerate power multiplication， and the algorithm is implemented by a computing architecture （CUDA）. The results show that the improved algorithm is more efficient.

Key words： Rivest-Smir-Adleman（RSA）algorithm；CUDA；improve Algorithm； mode power operation

隨着工业4.0的迈入，中国制造2025[1]与之不谋而合，应运而生。人们正在全面进入“互联网+”时代，中国制造2025“互联网+工业”是“互联网+”的重要组成部分之一。现阶段通过大规模定制和网络协同配置的各方面资源、数据越来越多，制造业企业的实时数据安全处理、传输和储存的要求也会越来越高，保障数据的实时安全传输是这个时代迫切需要的。可以说加密技术无疑是保障数据安全传输的重要措施之一。RSA公钥密码是1978年Ron Rivest， Adi Shamirh和LenAdleman提出来的，源于三个作者的首字母，该算法是公钥加密的行业标准[2]。RSA加密算法理论基础是两个大素数相乘，然而计算机技术的进步使得比较短的RSA密钥可以被攻破。所以，RSA的密钥在不断的加长。我国山东大学的研究人员季凯和他的破解团队成员刘强等人宣布找到了这样的一种快速素因子分解算法，并且公布了算法，但是并没有得到最终的证实。现在国内外在RSA算法的研究上主要集中在算法的优化和程序的优化上，在算法优化方面主要集中在模幂和模乘的快速算法上，最传统的方法。就是把乘方后求模的运算改为一边乘方一边求模的运算，这种方法最大化避免大数的乘方运算。在一定程度上提高RSA的效率[3]-[5]。

现阶段应用最为广泛的加密算法有MD5算法、DES算法及RSA算法[6]-[8]。MD5是将任意长度的“字节串”变换成一个128bit的大整数，并且它是一个不可逆的字符串变换算法。DES算法把64位的明文输入块变为64位的密文输出块。而RSA算法是第一个既能用于数据加密也能用于数字签名的算法，RSA的安全性一直未能得到理论上的证明，但是它经历了各种攻击，至今未被完全攻破。较之MD5、DES算法，RSA算法的安全性更高，它的安全性基于数论中的大素数分解，该体制是采用足够大的整数作模数。但是大整数分解问题运用了大量的模乘和幂运算时间都比较长，所以RSA密码体制有显著的缺点就是运算效率低下，运算时间过长等缺点。那么提高RSA的算法效率是研究RSA密码体制的重点。

在1976年，W.Diffie和M.E.Hellmam发表了具有划时代意义的“密码学的新方向”一文，提出了公钥密码体制思想，为近代密码学的发展指明了方向。它的出现是密码学研究领域中的一项重大突破，也是现代密码学诞生的标志之一[9]。本文针对物联制造数据的安全快速传输问题，提出了对RSA算法的改进。首先对非对称加密算法RSA进行了原理分析，进而提出了算法的改进和实现。

1 公开RSA加密算法

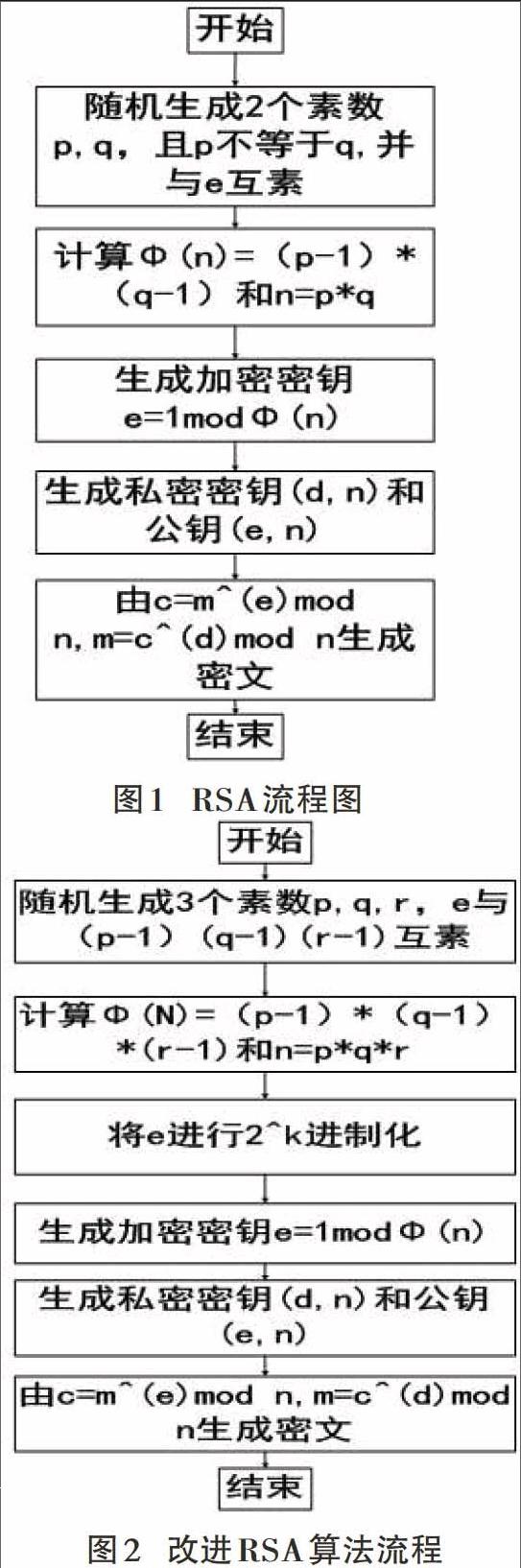
RAS算法是现今普遍使用的一种公开秘钥算法，其本质上是一种基于因数分解的非对称加密算法，其核心原理就是利用两个素数[10]。包含：一个是公钥以及一个是私钥，公钥是唯一解密通过私钥加密的密文，同时，私钥也是唯一解密通过公钥加密的密文，那么这就解决了数据的在传输过程中由于密钥的丢失，导致安全性受到威胁的问题。其加密算法流程如下：

从上述流程中不难看出中不难看出传统的RSA算法采用的公钥是n=p*q；并通过指数e二进制化后迭代，然后求模运算。

2 RAS算法的优化

2.1 RSA算法优化原则

由于传统的RSA的安全性依靠于算法过程中的大素数的因子分解的难度，也就造成了该算法采用的幂指剩余计算太耗时（在加密解密过程要计算大整数模幂乘）[11]。优化原则：（1）提高安全性，最大素数p和q至少应该是在100位以上的十进制数；（2）e的适当减小会加快解密速度，但是太小会威胁安全性。

2.2 优化RSA算法

2.2.1 多因子优化

利用多个素数因子对算法进行加速，此处选取三个素数因子，可以降低素数选取需要的时间，通过中国剩余定理[12]得出适当的减少素数的位数，可以降低计算量。那么基本算法描述如下：

首先选择三个保密大素数：p、q及r。计算n=p*q*r，[φ（n）=（p-1）（q-1）（r-1）]，[φ（n）] 为欧拉函数，选择整数e，有[gcd（φ（n），e）=1] ，计算[d*e=1modφ（n）]，以{e，n}为公开钥，{p，q，r}为密钥，与传统RSA相比较，若明文m大于n，则需将m分块使得每一块数据都小于n-1，进而进行c=m^emod n。

2.2.2 幂指运算优化

传统的RAS算法指数e的比特序列长度很大，需要在计算过程中多次迭代，因此找出最短的指数序列减少迭代次数是加速该算法的手段之一。那么，采用将指数e进行2^k进制化的方式达到加速算法的目的。

3 改进RSA算法实现

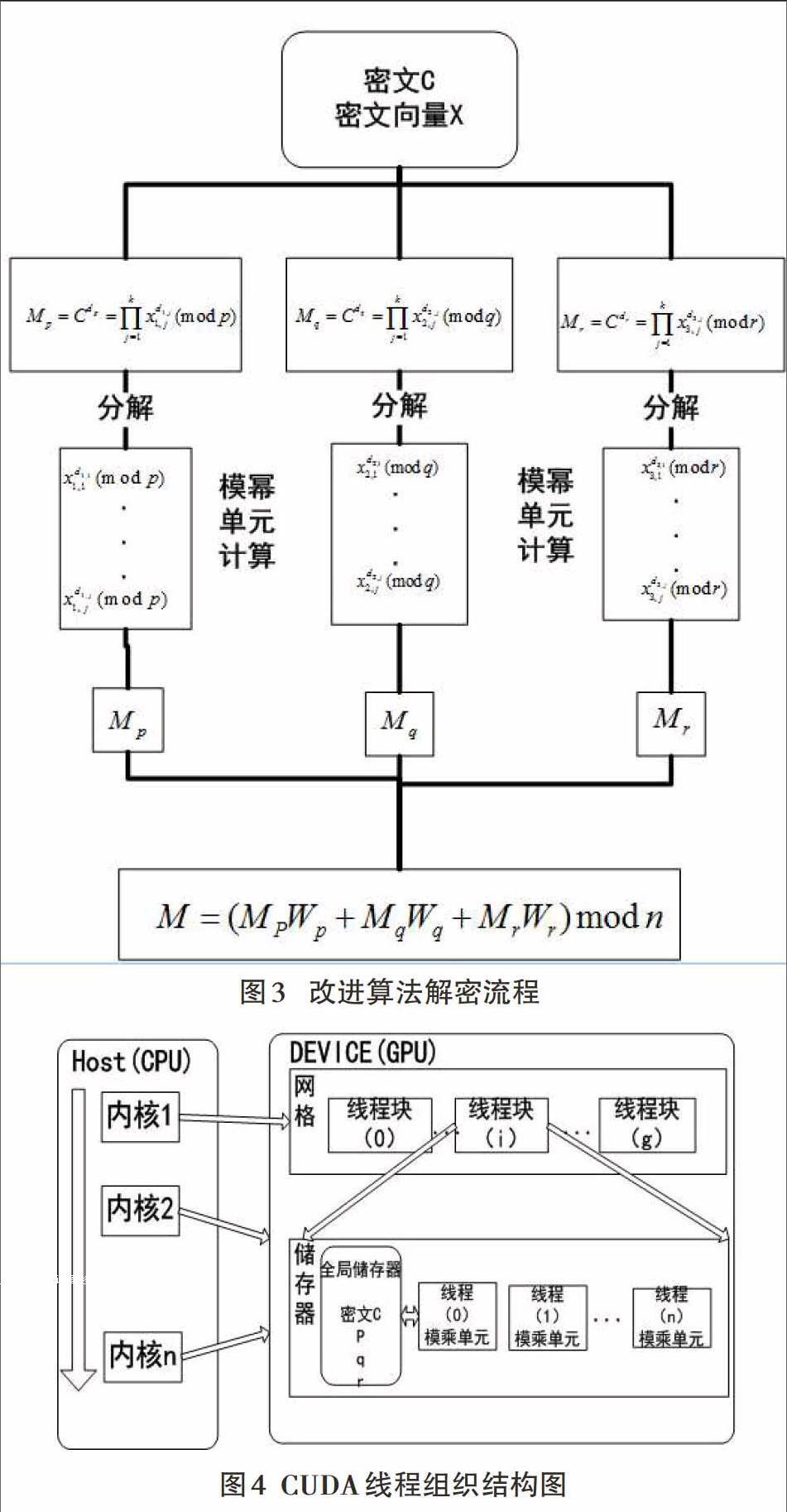
3.1 改进RSA模幂单元分析

3.2 基于CUDA的算法实现

3.3 具体实现方法

4 数据的验证分析

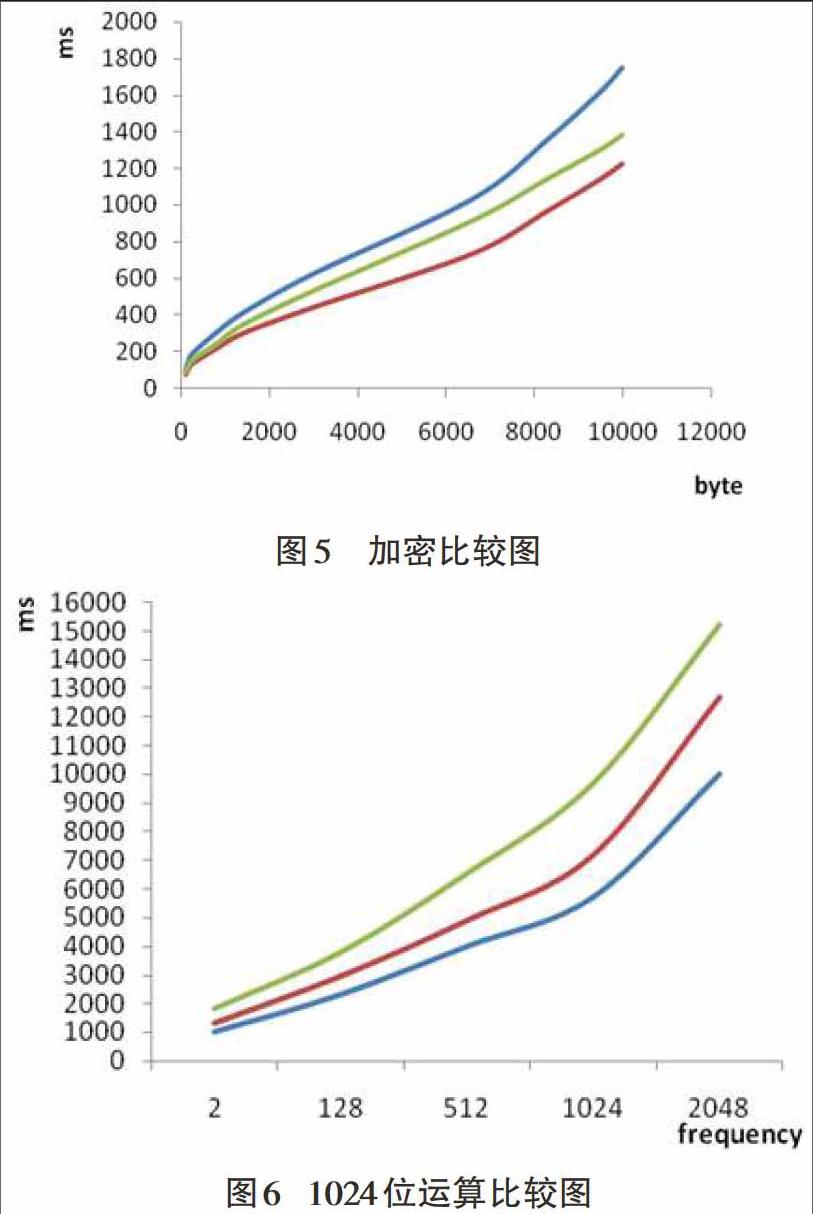
基于物联制造实验室，运用由NVIDIA公司开发的GeForce GTX960对采集的数据进行验证，首先对改进算法的加密过程进行了数据分析如下：

基于CUDA对RSA算法加密进行数据验证。最下方的曲线为所求曲线，从图中可以得出最下方的在加密过程中完全优于另外曲线。所以在采用三因子素数及幂指优化算法可以在很大程度上提高加密效率。

下面将基于CUDA模式下对大整数模幂的运算性能对三种算法分别进行对1024 和2048位从运算次数进行解密分析：

改进RSA算法的解密过程基于CUDA完。在CUDA模式下，令y={2，128，512，1024，2048…}为运算次数。y值的增加会使并行的线程块增加，运算的速度会越来越快。这里达到2048位运算依然流畅进行，但是随着位数的时候会由于GPU本身的最大计算能力而下降。因为线程块越多意味着对储存器的访问次数越多，从而降低计算能力。但是从2张比较图可以看出改进后的RSA算法（最下方曲线）的解密效率同样很高。

5 结束语

在数据与工业的密切结合的时代里，改进加密算法用以保障数据的安全十分重要。本文首先对传统BR算法进行了阐述，然后提出改进RSA算法，并且对改进算法进行了模幂单元分解，然后基于CUDA将模幂单元运算加载到GPU上的线程块进行了解密分析。结果分析表明，通过在GPU上对传统BR和幂指算法的对比，在·改进的RSA算法的运算效率显著提升。

参考文献：

[1] 黄群慧， 贺俊. 中国制造业的核心能力、功能定位与发展战略——兼评《中国制造2025》[J]. 中国工业经济， 2015（6）：5-17.

[2] A distributed algorithm to find safe RSA keys[M]// Distributed Programming Paradigms with Cryptography Applications. Springer Berlin Heidelberg， 1994：37-60.

[3] ALFRED J.MENEZES[加]. 应用密码学手册[M]. 电子工业出版社， 2005.

[4] 周玉洁， 冯登国. 公开密钥密码算法及其快速实现[M]. 国防工业出版社， 2002.

[5] 孙宝林， 杨球， 吴长海. RSA公开密钥密码算法及其在信息交换中的应用[J]. 武汉理工大学学报（交通科学与工程版）， 2000， 24（2）：169-172.

[6] 魏晓玲. MD5加密算法的研究及应用[J]. 信息技术， 2010（7）：145-147.

[7] 夏淑华. 基于DES和RSA加密算法的数据安全传输技术的研究[J]. 制造业自动化， 2011， 33（2）：180-182.

[8] 步山岳. RSA加密算法分析与实现[J]. 信息安全与通信保密， 2007（10）：80-81.

[9] 任伟. 现代密码学[M]. 北京邮电大学出版社， 2014.

[10] Kalpana P， Singaraju S. Data Security in Cloud Computing using RSA Algorithm[J]. 2012.

[11] Xin， Zhou， Xiaofei， et al. Research and implementation of RSA algorithm for encryption and decryption[C]// Strategic Technology （IFOST）， 2011 6th International Forum on. IEEE， 2011：1118 - 1121.

[12] 楊坤伟， 李吉亮， 张瑞丽. 中国剩余定理在密码学中的应用研究[J].计算机技术与发展，2014（1）：238-241.

[13] T?lke B J. Implementation of a Lattice Boltzmann kernel using the Compute Unified Device Architecture developed by nVIDIA， Computing and Visualization in Science 1–11[J]. 2010.

[14] 孙迎红， 童元满， 王志英. RSA算法的CUDA高效实现技术[J]. 计算机工程与应用， 2011， 47（2）：84-87.

[15] Sun D Z， Huai J P， Cao Z F. A comment on “An efficient common-multiplicand-multiplication method to the Montgomery algorithm for speeding up exponentiation”[J]. Information Sciences， 2013， 223（223）：331-334.