内皮调节对小动脉管腔运动影响的模型分析1)
2017-03-20唐元梁
唐元梁 贺 缨
(大连理工大学能源与动力学院,大连116024)
内皮调节对小动脉管腔运动影响的模型分析1)
唐元梁 贺 缨2)
(大连理工大学能源与动力学院,大连116024)
微循环是血液和组织之间发生物质交换的主要场所,它可以通过改变管径实现对血压、血流量的局部调节.血管内皮层对小动脉运动有重要的调节作用.本文基于连续介质假设,建立了内皮调节过程中主要活性物质在管壁中的扩散--反应动力学模型,并分析了非线性黏弹性血管的径向运动特性.利用该模型首先得到了内皮舒张因子一氧化氮(NO)、平滑肌细胞内钙离子(Ca2+)以及磷酸化肌球蛋白(actin-myosin complexes,AMC)在管壁内的的径向浓度分布;为分析内皮调节的动态过程,进一步对小动脉的被动舒张、血流量发生扰动时的管径响应分别进行了模拟.研究结果显示:当没有活性物质参与调节小动脉被动舒张时,管径无振荡发生;当血流量变化引起内皮调节时,内皮舒张因子NO浓度和管径均出现衰减振荡,振荡周期约60s.分析认为内皮调节对壁面剪切力的反馈控制,可能是NO浓度和管径产生周期性振荡的原因.内皮调节过程呈现的频谱特征可以为血管内皮功能障碍的诊断提供帮助.
剪切力,内皮调节,一氧化氮,糖尿病,微循环
引言
人体组织或器官的正常代谢功能需要通过适量的营养和氧的供给,以及代谢废物的及时排出来维持,生理状况下人体通过全身性的神经/体液调节以及微循环的局部血流调节,能够满足组织或器官的代谢需求[1].血管内皮层结构及功能的完整性对于微循环的局部血流调节非常重要.动脉粥样硬化、糖尿病等常伴有血管内皮功能障碍,造成人体局部血流调节机制失效.临床研究表明神经、大血管及微血管病变是两种类型糖尿病患者常见的慢性并发症[2].考察血管活性物质浓度变化对血管运动的影响有助于加深对血管管腔内皮调节机理的认识,进一步为相关代谢、血管疾病的早期诊断及治疗提供帮助.
1980年Furchgott等[3]发现内皮细胞对血管平滑肌细胞的舒张起重要作用.流动剪切力不仅影响和调控了内皮、平滑肌细胞的形状和排列取向,而且能刺激内皮细胞分泌多种信号分子影响平滑肌细胞的生理功能[4].依赖流动剪切力的内皮调节反应主要发生在人体的小动脉及比较大的微动脉[5],该反应可缓解甚至完全消除因肌源性反应造成的下游血管收缩、血流持续下降的问题[6];此外,由于代谢反应主要引起末梢微动脉的有限舒张,不能完全满足周围组织在代谢量增大时的血流需求,因此上游小动脉的内皮舒张反应能极大弥补末梢微动脉代谢调节反应的局限性.
目前一氧化氮(NO)被认为是剪切力诱导内皮细胞释放的最主要舒血管因子,NO的产生、传输及作用是影响血管内皮调节反应机制的关键.细胞内重要的第二信使Ca2+在内皮细胞NO合成过程中起到重要作用,剪切力或其他生化因子引起内皮细胞膜上Ca2+通道打开,内皮细胞合成NO增多.Li等[7-9]对剪切流与ATP(adenosine triphosphate,三磷酸腺苷)协同定量调控血管内皮细胞内Ca2+响应进行了理论和实验研究,通过控制剪切力或ATP信号较好地实现了对内皮细胞内Ca2+信号的定量控制.管壁内皮NO的产生研究方面,Liao等[10]通过实验获得了在无流动及有血流情况下血管不同的肌源性收缩反应,并基于实验数据建立了相关的内皮调节反应经验公式.Cornelissen等[11]建立了内皮分泌NO速率与壁面剪切力的S形函数关系,并进一步发展了NO浓度与冠状动脉树血管紧张度关系的数学模型.关于NO在管壁、管腔及周围组织的传输特性的研究工作方面,Chen等[12]构建了包含小动脉、毛细血管网及组织的三维NO传输模型,对NO在血液、血管壁及周围组织中的分布进行了模拟分析.结果表明壁面剪切力、红细胞压积、血管分叉等因素对NO的生成及分布均有影响.Liu等[13]基于流动模型和对流--扩散--反应方程对NO在狭窄血管中的传输进行了模拟分析.研究结果表明血管狭窄处的流动失稳对NO的传输有显著的影响,可能是造成动脉粥样硬化的重要因素.Tsoukias等[14]则对组织总肌红蛋白、血浆中血红蛋白对微循环周围NO的扩散影响进行了模型分析.
目前阶段研究者多采用唯象模型来研究小动脉血流调节反应,即不考虑具体的调节反应过程,只是概括地去总结和提炼实验结果.如Carlson等[15-17[18]建立了血管平滑肌运动的电化学--化学机械细胞模型,在细胞力学模型中加入了与主动收缩张力元件串联的黏弹性元件,随后Yang等[19]加入了平滑肌细胞内NO/cGMP(cyclic guanosine monophosphate,环磷酸鸟苷)反应模型,考察了NO的舒血管作用.Kudryashov等[20]基于连续介质模型,预测了NO、平滑肌细胞内Ca2+以及磷酸化肌球蛋白在管壁的稳态浓度分布,并通过改变血流量考查了模型的自动调节功能以及血管口径在向新平衡态发展过程中出现的振荡现象.
在人体的许多组织中,小动脉管径及血流的自发振荡现象被观测到,但是其生理意义及振荡机理仍不甚清楚.研究表明血流/皮肤温度振荡信号与相应调节反应间的频率具有对应关系,可以从皮肤温度振荡信号提取出内皮调节信号(0.0095~0.02Hz),(交感)神经调节信号(0.02~0.06Hz)及肌源性调节信号(0.06~0.15Hz)等[21-22].Smirnova等[23]对比了健康组、二型糖尿病组以及糖耐量受损患者的手部皮肤温度信号,发现无血管病变实验对象在手部受到冷水刺激时内皮、神经调节频段的温度波动幅值均减小,冷水刺激结束后波动幅值逐渐恢复;而二型糖尿病和糖耐量受损患者在结束冷水刺激后,相应频段的温度波动幅值并没有及时恢复.其认为这可能是由于微血管内皮功能障碍及神经病变引起的.由于多种调节反应可能共同参与血管的调节过程且互相影响,单纯的实验研究难以准确把握某一调节反应的内在机理,因此结合合适的数学模型对于管径调节机理的研究会有很大的帮助.
由于唯象模型不能够对内皮调节反应机制作出解释,本文将基于Kudryashov等[20]的工作对小动脉内皮调节功能进行模型分析.基于连续介质假设,对内皮调节过程主要介质在管壁中的两层扩散--反应动力学变化进行了建模,并考虑管壁的非线性黏弹性性质计算血管的径向运动.利用该模型本文将对给定血流条件下内皮舒张因子NO以及平滑肌细胞内Ca2+和AMC的径向浓度分布进行计算,进一步模拟血流变化引起的内皮调节反应过程,并对管径振荡的力学机制等进行讨论.
1 研究方法
1.1 小动脉壁力学性质及依赖剪切力的内皮调节反应生理机制
小动脉管壁由几种不同的组织构成.小动脉壁内膜表面是单层内皮细胞,中膜含有大量的平滑肌细胞.小动脉管壁的力学性质表现为非线弹性和黏弹性,同时平滑肌在生理控制下会提供收缩张力.
平滑肌细胞伸缩的初始刺激源是细胞内Ca2+浓度的变化.Ca2+引起平滑肌细胞收缩的过程可以描述如下[24]:平滑肌细胞内Ca2+与钙调蛋白结合;钙调蛋白与Ca2+结合物进一步与肌球蛋白激酶(一种磷酸化酶)结合且将其激活;在肌球蛋白激酶作用下,肌球蛋白头调节轻链磷酸化;轻链发生磷酸化后,肌球蛋白头对肌动蛋白丝进行间歇性的牵拉,从而引起平滑肌紧张并产生收缩力.
流动剪切力调节血管内皮细胞的代谢,使之合成血管活性物质NO等调节平滑肌细胞内Ca2+浓度及血管的紧张度.依赖剪切力的血管内皮舒张过程如图1所示:当血流量增加、管壁剪切力增大时,内皮细胞膜上Ca2+通道打开,内皮细胞合成NO增加;NO合成后扩散进入管壁平滑肌层;NO穿越平滑肌细胞膜进入细胞内部,刺激平滑肌细胞产生cGMP,后者能够引起细胞内Ca2+的外流;如前所述,Ca2+浓度对平滑肌细胞的收缩性和张力起到决定作用,其流失导致细胞内收缩性的肌动--肌球蛋白复合物浓度下降,最终导致平滑肌的松弛和张力的下降.
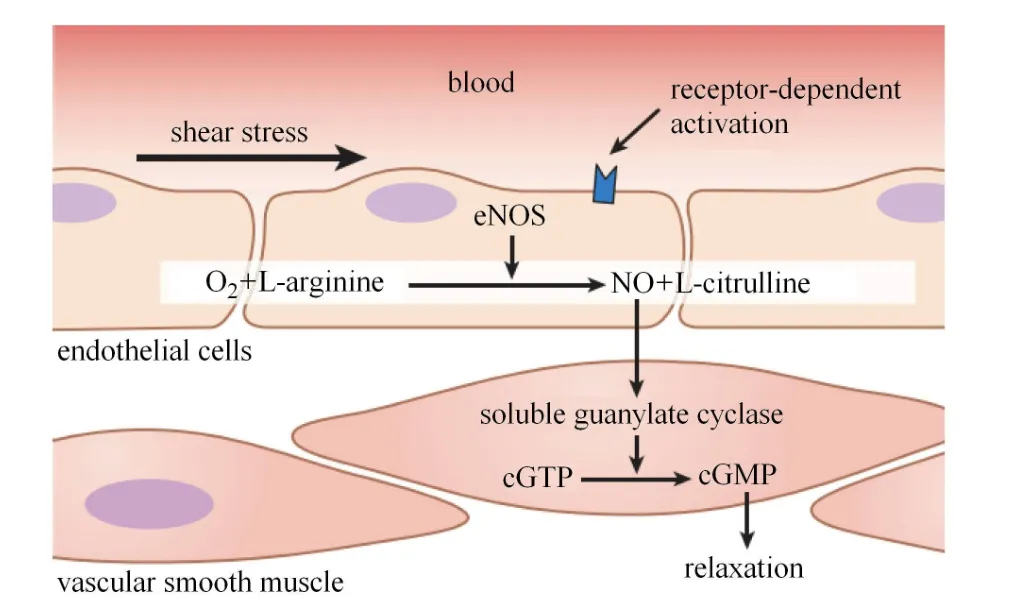
图1 血管内皮调节图示[24]Fig.1 Schematic of endothelial regulation[24]
1.2 数学模型
1.2.1 内皮层NO的产生
内壁面切应力的大小决定了内皮细胞产生NO的速率,轴向血流速度分布采用Hagen--Poiseuille模型,给定血流量Q,则内壁面剪切应力τsh(t)可以表示为
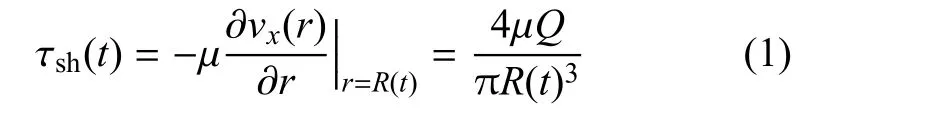
式中,r为径向坐标,R(t)为血管内径,µ为血液黏度,vx(r)为轴向流速,Q为血液体积流量.内壁面切应力的大小决定了内皮细胞产生NO的速率,此外血液--特别是血液中的血红蛋白,会消耗一部分内皮细胞产生的NO,因此内皮层NO浓度的变化可用常微分方程(2)描述

式中ne内皮层NO的浓度,等式右边第1项为血流对NO的消耗率,ke为NO在血液中的消耗系数;右边第2项表示剪切力依赖的内皮NO产生率,其与壁面剪切力τsh(t)成正比,k1为产生系数.也有研究者[11]认为NO的产生率与壁面剪切力成S形曲线关系.血液中消耗NO的主要成分是血红蛋白,其消耗速率与血液的流变学参数相关,在本文中ke与k3均设为常数.将壁面剪切力式(1)代入方程(2)中,并引入管径相对扰动量η=(R-R0)/R0替代管径R,其中R0为参考半径,得到
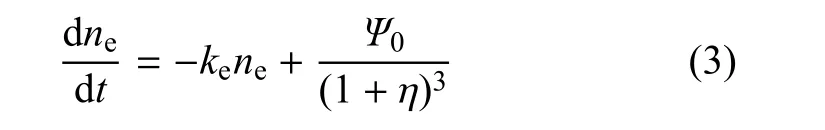
1.2.2 管壁NO的传输
NO在内皮细胞合成后,经过扩散和生物化学反应在管壁中传输.内膜和中膜NO浓度变化的动力学过程可以表示为如下方程
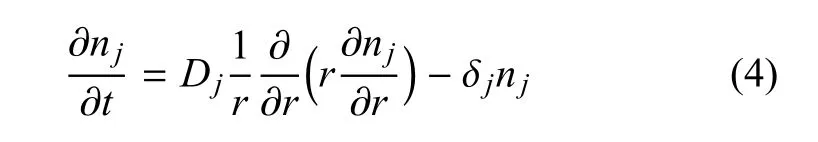
其中,j=1,2时分别表示管壁的内膜、中膜,nj为管壁NO浓度.方程右边第1项为扩散项,Dj为NO在管壁中的扩散系数;第2项为NO在管壁的反应项.与血液对NO的消耗类似,模型认为NO在管壁的反应速率与NO浓度成正比,δj为NO在管壁的反应系数.利用式(3)可以给出内皮层的NO浓度并将其作为管壁内边界(r=Ri)的边界条件;内膜与中膜交界面(r=Rm)上NO浓度及扩散量均保持连续;在中膜外边界(r=Ra)上,假设NO不外扩散.上述边界条件描述为
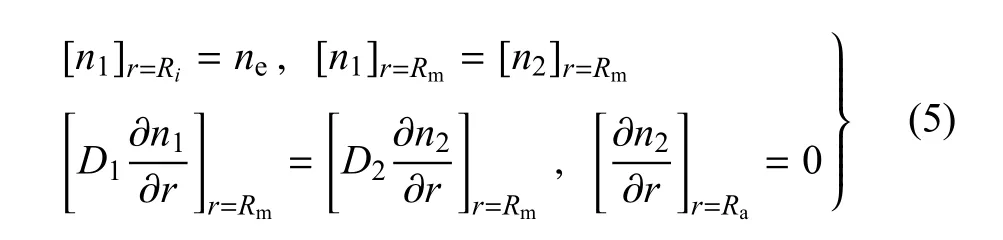
式中D1和D2分别为血管内膜、中膜的NO扩散系数.方程(3)、方程(4)、边界条件(5)及合适的初值条件构成了完整的动脉管壁NO扩散--动力学反应双层模型.
1.2.3 平滑肌Ca2+与磷酸化肌球蛋白浓度
平滑肌细胞内Ca2+的浓度变化由平滑肌细胞质Ca2+的净流量决定.平滑肌细胞质中Ca2+源包括细胞间质、细胞内的细胞器--肌质网.与骨骼肌细胞不同,血管平滑肌细胞的肌质网并不发达,平滑肌细胞质Ca2+的主要来源是细胞间质.由于细胞间质Ca2+浓度远高于平滑肌细胞内(约104倍),Ca2+可通过平滑肌细胞膜上的Ca2+通道进入细胞内.该动力学过程可以用方程(6)描述
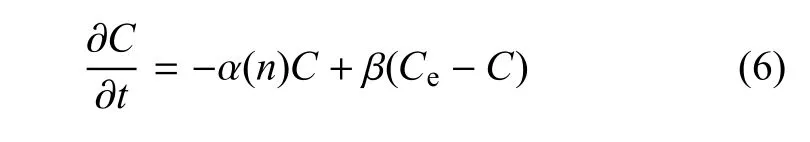
式中,C为平滑肌细胞质内Ca2+浓度,方程右边第一项为Ca2+向细胞外的主动运输,主动运输系数α(n)受平滑肌层NO浓度影响,α(n)=α1+k2n2(r,t);第二项为Ca2+的被动运输过程.β为传输系数,当跨壁压差不变时,β取为常数.Ce为细胞间质Ca2+浓度.因Ce≫C,可将方程(6)简化为
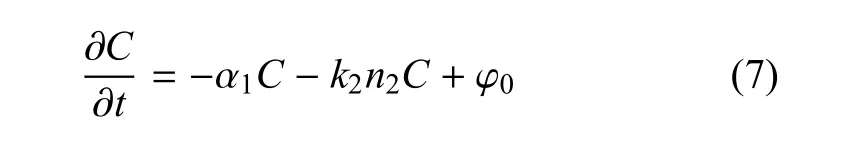
其中φ0=βCe.
平滑肌细胞内磷酸化肌球蛋白的浓度直接决定了平滑肌细胞的收缩性及主动张力的大小.其磷酸化程度(即浓度大小)由细胞内Ca2+浓度、阈值浓度及脱磷酸化速率共同决定.该动力学过程可以描述为
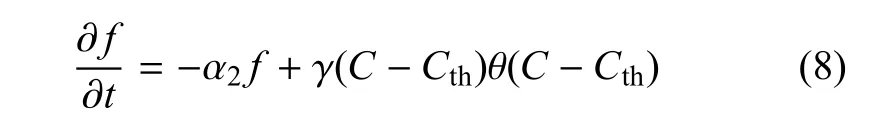
式中f为磷酸化肌球蛋白浓度,方程右边第1项表示肌球蛋白脱磷酸化过程,α2为脱磷酸化系数;第2项表示Ca2+依赖的肌球蛋白磷酸化,Cth为Ca2+阈值浓度,γ为磷酸化系数,θ为Heaviside单位函数
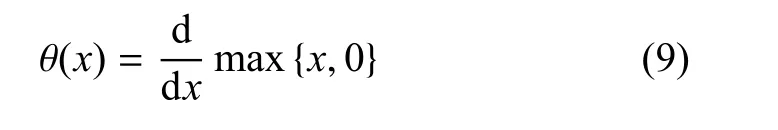
1.2.4 管壁径向运动
图2所示为管壁受力状态,从图2可以看出,小动脉的管径由跨壁压差P0=P-Pe(P和Pe分别为管内、外压力)、管壁周向张力T决定.
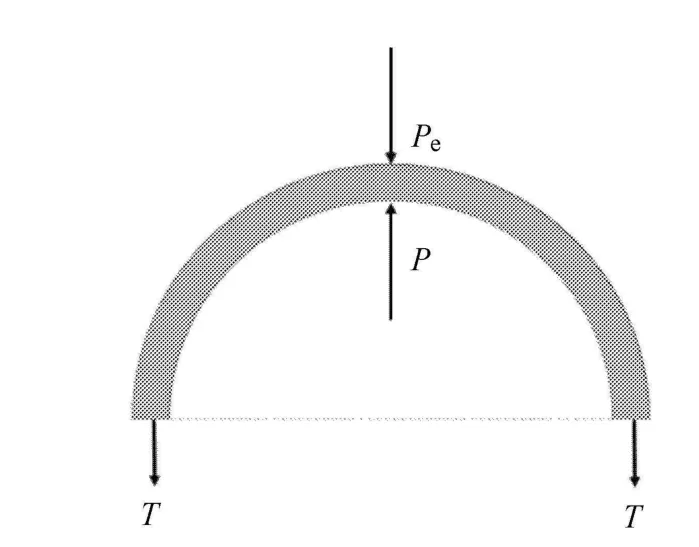
图2 管壁受力状态Fig.2 Stress condition on vessel wall
对于质量为Δm、半径为R的血管单元,根据动量守恒,有
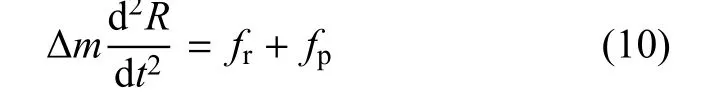
式中Δm=ρw2πRΔxh,ρw为血管密度,h为壁厚,Δx为血管单元的长度,fr和fp分别为管壁周向张力T、跨壁压差P0产生的径向力.fr和fp可分别表示为
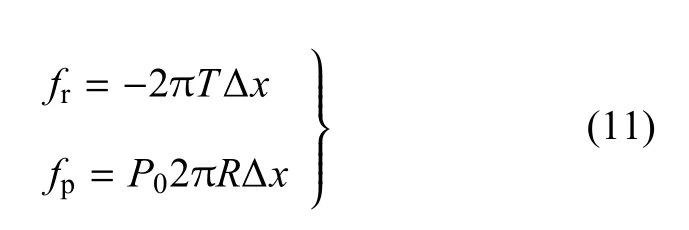
外力平衡时有fr+fp=0,代入方程(11)可得T=PR0,即周向张力与跨壁压差满足拉普拉斯定律.当血管为薄壁管时,管壁周向应力可认为均匀分布,即T=σθθh,其中σθθ为管壁平均周向应力.考虑动脉壁的非线弹性、黏性及平滑肌产生的主动收缩张力等情况,σθθ可以表示为
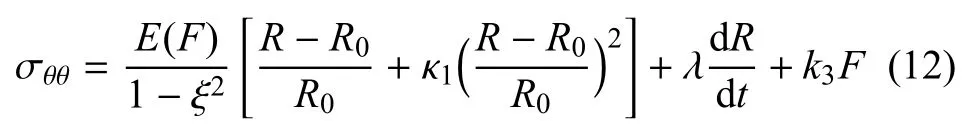
式中ξ为泊松比,κ1为非线性弹性系数,λ为黏性系数.方程右边最后一项为平滑肌主动收缩张力,其与平滑肌磷酸化肌球蛋白的体积平均浓度F成正比,k3为比例系数.管壁杨氏模量E(F)的大小也与F有关(E(F)=E0(1+εF/F0),F0为跨壁压差P0=15.332kPa),Ψ0=0.1µmol/s时磷酸化肌球蛋白的体积平均浓度,E0为不考虑平滑肌主动张力时的杨氏模量.
将式(11)和式(12)代入式(10),并引入血管半径的相对扰动量η=(R-R0)/R0,可以得到关于半径相对扰动量η的方程
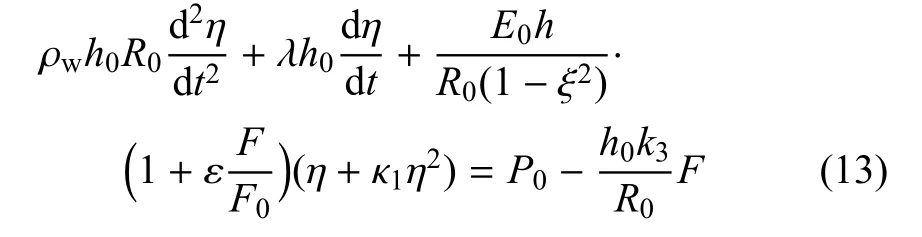
1.3 参数选取与数值方法
式 (13)中的参数 λ = 1.5E0t0/R0单位为kg·m-2s-1,其中t0=10s;k3=P0R0/(F0h0)[20].其他参数的取值及来源如表1所示.

表1 模型参数Table 1 Model parameters
引入如下无量纲参数对模型进行无量纲化处理
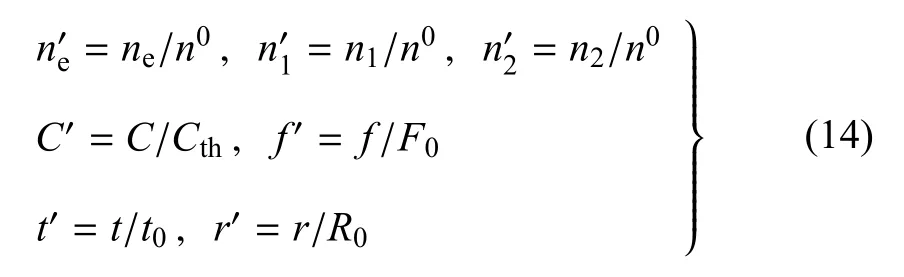
其中特征参数n0=0.1µmol/L,Cth=0.1µmol/L.R0=2mm为跨壁压差P0=15.332kPa,Ψ0=0.1µmol/s时的血管内径.最后得到相应的无量纲模型为
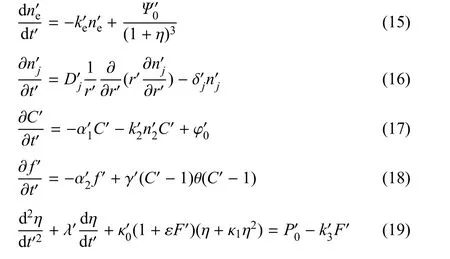
采用有限差分法对上述模型进行数值求解.对方程(16)扩散项进行空间中心差分离散,并进行隐式求解,采用共轭梯度法进行迭代;方程 (15)、方程(17)、方程(18)均采用欧拉隐式格式求解;对方程(19)惯性项、黏性项进行中心差分离散.无量纲时间、空间步长分别为Δt′=3.0×10-5和Δr′=1.2×10-3.
2 结果分析
2.1 内皮调节主要介质浓度的稳态分布
基于上述模型,首先得到了Ψ0=0.1µm/s时内皮调节主要介质浓度在管壁的稳态分布.如图3所示,由于内皮细胞是管壁NO的唯一产生源,在内皮层的NO浓度最高;沿管径向外,随着r′的增大,NO浓度因在管壁的反应消耗而逐渐降低(中膜外层的NO浓度为0.9030).平滑肌细胞内Ca2+浓度沿径向方向略有上升(中膜内层浓度为1.1296,中膜外层浓度为1.1314),这反映了舒血管物质NO的浓度变化与Ca2+变化相反,NO浓度的增大会造成平滑肌细胞内Ca2+浓度的下降.由于Ca2+浓度高于敏感阈值(Cth=0.1µmol/L),Ca2+浓度依赖的肌球蛋白磷酸化作用处于激活态,因此沿径向磷酸化肌球蛋白浓度也随Ca2+浓度的上升而略有增大(中膜内层浓度为0.9969,中膜外层浓度为1.0104).

图3 内皮调节主要介质在管壁内的径向浓度分布Fig.3 Stationary concentration distributions in the arterial wall of the key agents
2.2 血管的被动舒张
当管壁NO或其他舒血管物质浓度上升时,平滑肌细胞内Ca2+浓度会逐渐下降并可能低于阈值浓度Cth.此时平滑肌完全放松,主动收缩张力消失,动脉壁模型退化为完全被动的黏弹性管,此时管径相对扰动变化方程(13)变为
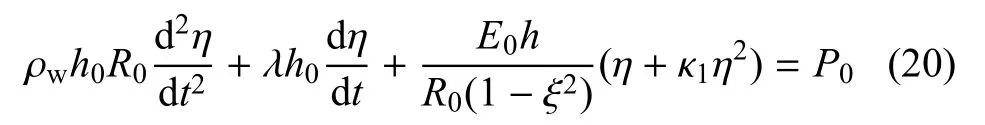
在η(0)=0的初始状态下,管壁周向应力减小使得跨壁压差与周向应力不平衡,管径会发生被动扩张.文献[20]给出了血管被动扩张模型的解析解,其形式为
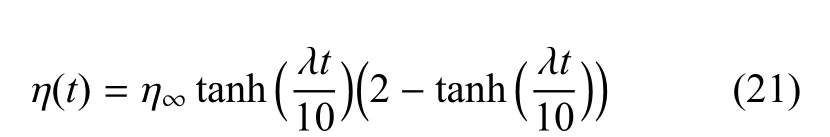
图4为该解析解与我们得到的数值解的比较.结果表明管径从初始状态η(0)=0经过被动扩张过程后达到新平衡态η=1.2511,数值解与精确解吻合较好.
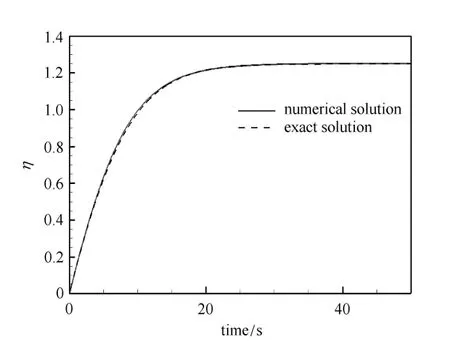
图4 管壁的被动扩张变化Fig.4 Passive dilatation of the artery
2.3 血流量变化时的内皮调节过程
由方程(2)可知,当管内血流量变化时,壁面剪切力依赖的内皮NO合成会发生改变,并影响到血管平滑肌的收缩张力、管径大小.将Ψ0=0.1µmol/s时血管管径、内皮调节主要介质的稳态浓度作为初始条件,对血流量发生变化时管径的内皮调节过程进行了模拟分析.
图5为血流量增加25%时模型的响应情况.管壁NO浓度均从初始态开始经过衰减振荡,逐渐稳定于新的平衡态浓度.血管管径也呈现衰减振荡,最终在新平衡态(η1.25=0.0536)稳定下来,此时跨壁压差与管壁周向应力达到平衡.结果显示NO浓度、管径的振荡周期均为60s左右,这与依赖内皮的血流调节频率相一致(0.0095~0.02Hz[21]).
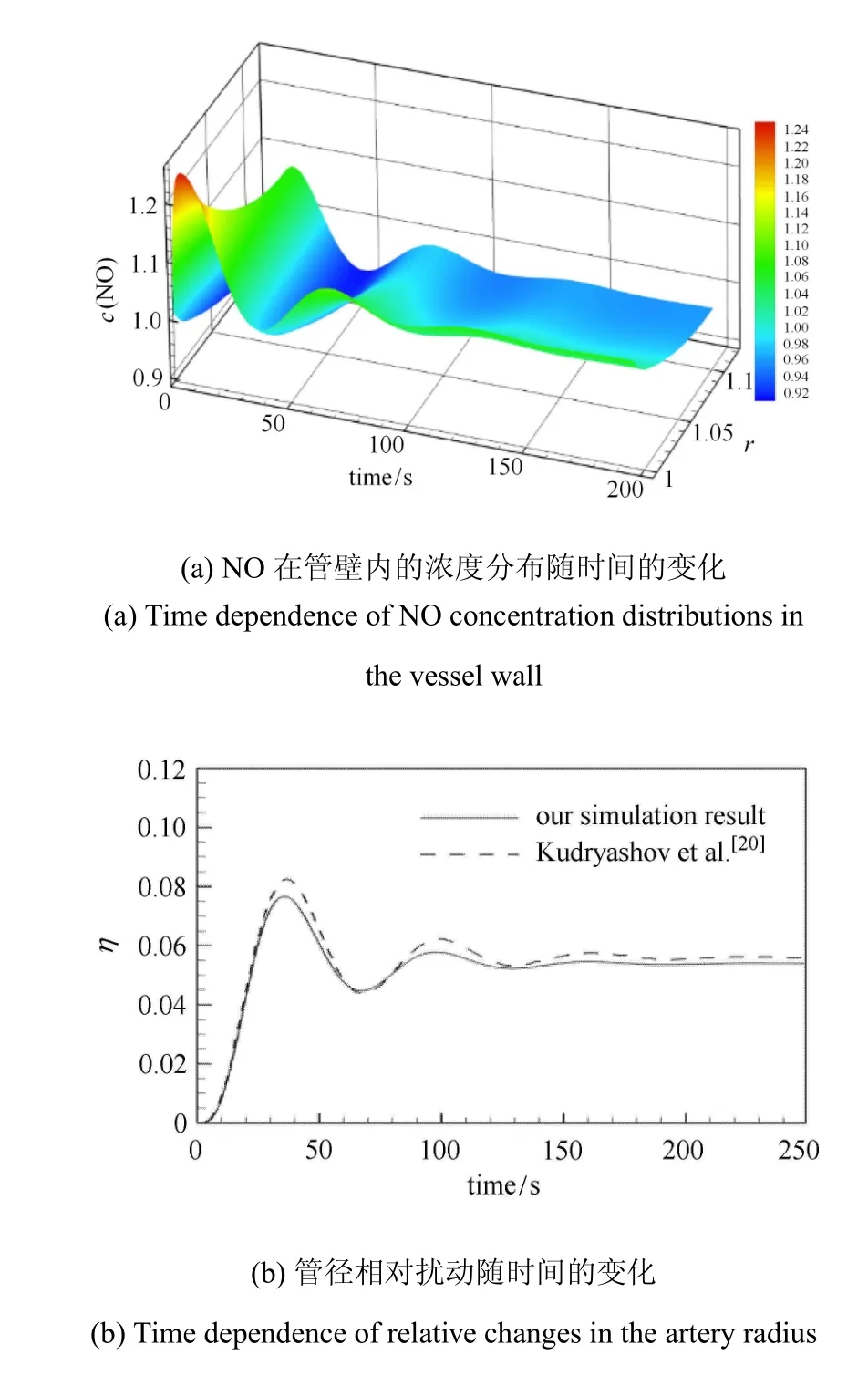
图5 NO浓度和管径随时间的变化Fig.5 Time dependence of the changes of NO concentration and artery radius
表 2列出了不同血流条件下小动脉达到新平衡态时的管径扰动量和壁面剪切力.从该表可以看到,管径扰动和壁面剪切应力随血流量增加呈非线性增加.当血流量Q由0.75Q0增大到1.50Q0时,壁面剪切力τsh只增大了0.20τ0.由式(1)可知,当管径无变化(即η=0)时,壁面剪切力τsh会随血流量Q的增大而线性增大;内皮调节引起的管径增大在很大程度上限制了τsh的快速上升,这对于维持血管内皮受力的相对稳定性非常重要.反之,若壁面剪切力τsh维持不变,由式(1)可得则管径扰动随血流量变化曲线斜率随血流量Q增大而逐渐减小.如图6实线所示,利用内皮调节模型得到的数据也呈现了类似的特征,说明内皮调节的作用是使血管管壁切应力尽量保持稳定.

表2 不同血流量条件下管径和壁面剪切力的响应Table 2 Responses of vessel radius and shear stress under dif f erent fl w conditions
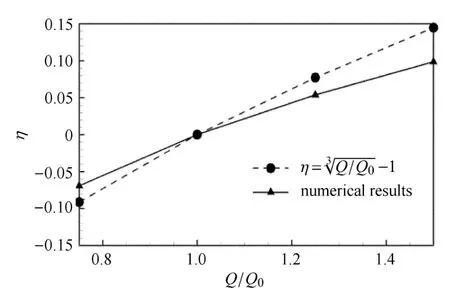
图6 管径扰动随血流量的变化Fig.6 Changes of artery radius under dif f erent fl w conditions
3 讨论
3.1 管径振荡变化的产生机理
通过模型分析可看出,血流量变化时,内皮舒张因子NO和管径会产生大周期振荡.为探究该振荡发生的原因,本文进一步对活性物质动力学特性和血管运动的相互作用进行了分析.
在血管管径运动方程(13)中我们考虑了血管的惯性、黏性及弹性.这些力学性质的组合可能会产生管壁阻尼振荡运动.阻尼运动方程的一般形式为

另一方面,若假设血管管径无变化(η=0),则根据方程(15)~方程(18)得到的平滑肌细胞内NO,Ca2+及磷酸化肌球蛋白浓度变化如图7所示.它们均从初始态平缓过渡至新的平衡态,无振荡出现.
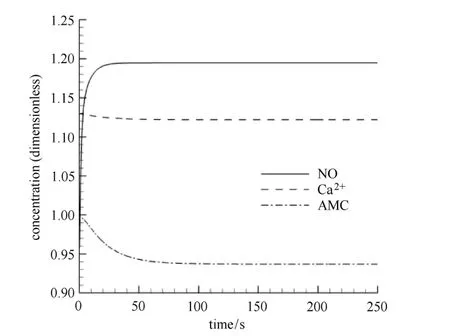
图7 内皮调节介质浓度随时间的变化(η=0,Q=1.25Q0)Fig.7 Variations of key agents’concentrations(η=0,Q=1.25Q0)
上述分析表明,血管管径、内皮调节活性物质浓度均不会独立地产生振荡变化,这种振荡可能是由于对壁面剪切力的负反馈控制作用而产生.图8描述了这一负反馈控制过程示意图,本文所采用模型很好地体现了这一特点.
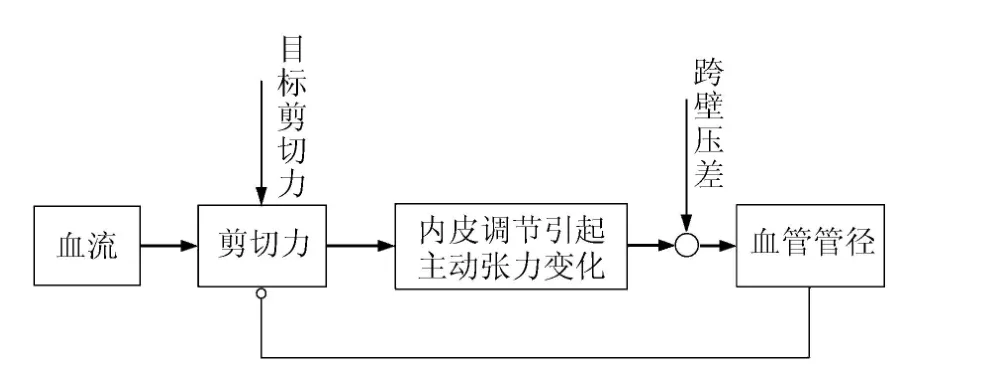
图8 内皮调节过程的剪切力反馈控制Fig.8 Feedback control of shear stress in the process of endothelial regulation
血管的自发振荡现象需要管壁平滑肌紧张度的协同变化,而能够在血管尺度迅速引发这一响应的方式极有可能是电信号在细胞之间的传输[28].有研究认为膜电势及细胞内Ca2+浓度的振荡变化是引起细胞紧张度变化的原因,这些电信号位于血管分叉处少量的特殊“起搏器”细胞内[29].Secomb[30]总结前人工作指出血管自发振动机理的两种可能性:血管壁细胞本身固有振动特性,即“起搏器”性质;管壁振荡运动由细胞反应、管壁力学性质以及血液流动之间的相互作用引起.Kvernmo等[31]认为内皮活动频率或反映了内皮释放血管活性物质的速率,或反映了平滑肌细胞对这些物质的响应频率.本文模型基于宏观连续介质假设,不能从细胞/细胞群尺度分析血管振荡的内在机理,但该模型体现了对壁面剪切力的反馈控制特点,使得内皮舒张因子NO、平滑肌内Ca2+、磷酸化肌球蛋白浓度以及血管管径逐步得到校正.因此我们推测内皮调节过程的反馈控制特点可能是内皮舒张因子NO、管径周期性振荡的原因;反馈环节的缺失使得振荡消失.
3.2 模型的特点和局限性
本文发展的内皮调节模型将活性物质浓度变化与血管周向张力、血管管径变化关联起来.相比于一般的唯象模型,本模型能够体现内皮调节反应过程,而且不涉及过于复杂的单个细胞内的具体反应机理,有助于我们加深对血管管腔内皮调节机理的认识.同时本模型有如下几个方面需要说明和进一步改进.
本文所采用的活性物质反应动力学模型与Kudryashov等[20]的模型相同,但在分析小动脉径向运动时,考虑到方程(13)中惯性力项的作用很小,又发现内皮调节引起的管径大周期波动并不是来自于管壁的机械振荡,因此在模型分析中略去了该惯性项.相较于Kudryashov等[20]的工作,本模型对血管运动振荡特性的分析更深入.
在流体介质方面,本模型假设血液为牛顿流体.采用牛顿流体假设会对壁面切应力的大小有一定影响,但不会影响活性物质在管壁的分布规律和管壁运动特性.
目前,本模型假定内皮NO的释放率与壁面剪切力成正比(k1τsh),且k1假定为定值.当内皮发生功能障碍时,NO的释放减少,模型中对应的比例系数k1也会相应减小,最终会影响血管正常的内皮舒张功能和壁面剪切力的维持.类似地,本模型假定血液对NO的消耗率与内皮NO浓度呈正比其中ke为定值.NO在血液中的传输和反应实际上与血液流速、红细胞压积、红细胞膜的渗透性等因素有关,这些因素的变化会改变ke的取值.在另外的研究中[32],建立了内皮NO在血液和组织中的反应—对流扩散模型,并对ke的影响进行了考察,发现ke的增大会使壁面NO浓度降低;同时,也在考察红细胞运动,变形和压积对NO生成的影响,这些结果会为确定不同状态下血液对NO的消耗率提供很好的数据支撑.
4 结论
本文结合扩散、反应动力学模型和黏弹管模型,对剪切力依赖的小动脉内皮调节反应进行了模拟,并对调节引起的振荡现象进行了分析.基于连续介质假设模型对管壁内皮层NO的产生和NO在管壁中的两层扩散--反应动力学过程、平滑肌细胞内Ca2+及磷酸化肌球蛋白的反应动力学过程进行了数学描述;考虑管壁的黏弹性并结合内皮调节产生的主动张力变化,建立了血管的径向运动模型.研究结果表明小动脉被动舒张过程管径无振荡发生,而血流量变化引起的内皮调节使内皮舒张因子NO浓度和管径均出现衰减振荡.本文认为内皮调节对壁面剪切力的反馈控制,可能是NO浓度—管径产生周期性振荡的原因.
内皮调节过程呈现的频谱特征可以为内皮功能障碍的诊断提供帮助.内皮功能受损常见于糖尿病发病早期.糖尿病内皮功能障碍的确切机制还不明确,高血糖造成的多种因素可能参与了内皮的受损过程,包括NO的产生、传输及效应环节,即:NO合成下降,NO扩散至平滑肌细胞层的功能受损,平滑肌细胞对NO反应性下降或内皮衍生的收缩因子抑制了血管舒张.合适的数学模型可以实现对上述环节的合理描述,通过模型分析可有助于对内皮功能受损原因的排查.
1 Davis MJ,Hill MA,Kuo L.Local Regulation of Microvascular Perfusion.Comprehensive Physiology,2010
2 Bohlen,Glenn H.Microvascular Consequences of Obesity and Diabetes.Comprehensive Physiology,2010
3 Furchgott RF,Zawadzki JV.The obligatory role of endothelial cells in the relaxation of arterial smooth muscle by acetylcholine.Nature,1980,288(5789):373-376
4 任长辉,刘肖,康红艳等.剪切力条件下血管内皮细胞与平滑肌细胞的相互作用.医用生物力学,2015,30(2):185-191(Ren Changhui,Liu Xiao,Kang Hongyan,et al.Interactions between vascular endothelial cells and smooth muscle cells under shear stress.Journal of Medical Biomechanics,2015,30(2):185-191(in Chinese))
5 Pohl U,De WC,Gloe T.Large arterioles in the control of blood fl w:role of endothelium-dependent dilation.Acta Physiologica Scandinavica,2000,168(168):505-510
6 Koller A,Kaley G.Endothelial regulation of wall shear stress and blood fl w in skeletal muscle microcirculation.American Journal of Physiology,1991,260(260):862-868
7 LiLF,ChengX,QinKR.ModelingofTRPV4-C1-mediatedcalcium signaling in vascular endothelial cells induced by flui shear stress and ATP.Biomechanics&Modeling in Mechanobiology,2015, 14(5):1-15
8 陈宗正,覃开蓉,高争鸣等.用于分析剪切力和生化因子对细胞联合作用的微流控装置.水动力学研究与进展,2015,30(6):643-649 (Chen Zongzheng,Qin Kairong,Gao Zhengming,et al.A microflu idic device for analyzing cellular behavior in response to shear stress and biochemical factors.Chinese Journal of Hydrodynamics,2015, 30(6):643-649(in Chinese))
9 高争鸣,覃开蓉,陈宗正等.剪切力和ATP定量调控血管内皮细胞钙信号的数值仿真研究.水动力学研究与进展,2015,30(6):679-684(Gao Zhengming,Qin Kairong,Chen Zongzheng,et al. Numerical simulation research on quantitative regulation of intracellular Ca2+signals in vascular endothelial cells via shear stress and ATP modulation.Chinese Journal of Hydrodynamics,2015,30(6):679-684(in Chinese))
10 Liao JC,Kuo L.Interaction between adenosine and fl w-induced dilation in coronary microvascular network.AJP Heart&Circulatory Physiology,1997,272(4Pt2):H1571-H1581
11 Cornelissen AJ,Dankelman J,Vanbavel E,et al.Balance between myogenic,fl w-dependent,and metabolic fl w control in coronary arterial tree:a model study.AJP Heart&Circulatory Physiology, 2002,282(6):H2224
12 Chen X,Buerk DG,Barbee KA,et al.3D network model of NO transport in tissue.Medical&Biological Engineering&Computing,2011,49(6):633-647
13 Liu X,Fan Y,Xu XY,et al.Nitric oxide transport in an axisymmetric stenosis.Journal of the Royal Society Interface,2012,9(75):2468-2478
14 TsoukiasNM,PopelAS.Amodelofnitricoxidecapillaryexchange.Microcirculation,2003,10(6):479-495
15 Carlson BE,Secomb TW.A theoretical model for the myogenic response based on the length-tension characteristics of vascular smooth muscle.Microcirculation,2005,12(4):327-338
16 Arciero JC,Carlson BE,Secomb TW.Theoretical model of metabolic blood fl w regulation:roles of ATP release by red blood cells and conducted responses.AJP Heart&Circulatory Physiology,2008,295(4):H1562-H1571
17 Carlson BE,Arciero JC,Secomb TW.Theoretical model of blood fl w autoregulation:roles of myogenic,shear-dependent,and metabolic responses.AJP Heart&Circulatory Physiology,2008, 295(4):H1572-H1579
18 Yang J,Jr J C.The myogenic response in isolated rat cerebrovascular arteries:smooth muscle cell model.Medical Engineering&Physics,2013,25(8):691-709
19 Yang J,Clark JW,Bryan RM,et al.Mathematical modeling of the nitric oxide/cGMP pathway in the vascular smooth muscle cell.AJP Heart&Circulatory Physiology,2005,289(2):H886-H897
20 Kudryashov NA,Chernyavskii IL.Numerical simulation of the process of autoregulation of the arterial blood fl w.Fluid Dynamics, 2008,43(1):32-48
21 Kvernmo HD,Stefanovska A,Bracic M,et al.Spectral analysis of the laser doppler perfusion signal in human skin before and after exercise.Microvascular Research,1998,56(3):173-182
22 Sagaidachnyi AA,Usanov DA,Skripal AV.Correlation of skin temperature and blood fl w oscillations//Proceedings of SPIEThe International Society for Optical Engineering,2011,8337(4):83370A-83370A-8
23 Elena S,Sergey P,Irina M,et al.Assessment of endothelial dysfunction in patients with impaired glucose tolerance during a cold pressor test.Diabetes&Vascular Disease Research Of ficial Journal of the International Society of Diabetes&Vascular Disease,2013, 10(6):489-497
24 Hall JE.Textbook of Medical Physiology.13th Edn.Oxford:Elsevier Ltd,2016.203-214
25 Formaggia L,Lamponi D,Quarteroni A.One-dimensional models for blood fl w in arteries.Journal of Engineering Mathematics, 2003,47(3-4):251-276
26 Regirer SA,Nkh S.Mathematical models of nitric oxide transport in a blood vessel.Biofizik,2005,50(3):515-536
27 Snow HM,Mcaulif f e SJ,Moors JA,et al.The relationship between blood fl w and diameter in the iliac artery of the anaesthetized dog:the role of endothelium-derived relaxing factor and shear stress.Experimental Physiology,1993,16(3):278-282
28 Nilsson H,Aalkjaer C.Vasomotion:mechanisms and physiological importance.Molecular Interventions,2003,3(2):79-89,51
29 Goligorsky MS,Colfles D,Gordienko D,et al.Branching points of renal resistance arteries are enriched in L-type calcium channels and initiate vasoconstriction.American Journal of Physiology,1995, 268(2 Pt 2):F251
30 Secomb TW.Theoretical models for regulation of blood fl w.Microcirculation,2008,15(8):765-775
31 Kvernmo HD,Stefanovska A,Kirkeboen KA,et al. Oscillations in the human cutaneous blood perfusion signal modifieby endothelium-dependent and endothelium-independent vasodilators.Microvascular Research,1999,57:298-309
32 Wei YJ,He Y,Tang YL.Finite element analysis on NO transport in system of permeable capillary and tissue//11th Asian Computational Fluid Dynamics Conference.Accepted
MODEL ANALYSIS OF ENDOTHELIUM-DEPENDENT VASOMOTION OF SMALL ARTERY1)
Tang Yuanliang He Ying2)
(School of Energy and Power Engineering,Dalian University of Technology,Dalian116024,China)
Metabolic substance exchange between blood and tissue occurs mainly in microcirculation,which can locally regulate blood pressure and blood fl w by changing their diameters.Vascular endothelium plays an important role in the vasomotor regulation of small artery.In this paper,a model was adopted to study the endothelial regulation mechanism. Based on the continuum assumption,two layers of dif f usion&kinetic processes of key agents in endothelial regulation were modeled,and the nonlinear viscoelastic properties of the wall material were considered in the computation of radial motion of small artery.The stationary distributions of nitric oxide(NO),calcium ion(Ca2+)and the contracting actinmyosin complexes(AMC)concentrations in the wall were firstl obtained;then the process of arterial passive dilation and the autoregulation process to the disturbance of blood fl w were simulated.Numerical results showed that there was no oscillation of arterial diameter occurred during the passive dilation process.However,when there was a change in blood fl w,the whole system transferred from the initial state to a new equilibrium state with slow damped oscillations. The oscillating period was about 60s.It is supposed that the endothelial oscillation of artery diameter and NO concentration occurring during the dynamic regulating process is caused by the feedback control of shear stress.This oscillationcharacteristic can provide useful information for the diagnosis of endothelial dysfunction.
shear stress,endothelial regulation,nitric oxide,diabetes,microcirculation
R318.01
A doi:10.6052/0459-1879-16-171
2016-06-13收稿,2016-09-29录用,2016-10-18网络版发表.
1)国家自然科学基金(51576033)和大连市科技计划(2015F11GH092)资助项目.
2)贺缨,教授,主要研究方向:血液动力学,生物传热传质.E-mail:heying@dlut.edu.cn
唐元梁,贺缨.内皮调节对小动脉管腔运动影响的模型分析.力学学报,2017,49(1):182-190
Tang Yuanliang,He Ying.Model analysis of endothelium-dependent vasomotion of small artery.Chinese Journal of Theoretical and Applied Mechanics,2017,49(1):182-190
