变风量空调系统送风管道静压特性的试验研究

丁 帅，孟庆龙，王博闻，谢安生，赵 凡

(长安大学 旱区地下水文与生态效应教育部重点实验室，陕西西安 710054)

变风量空调系统送风管道静压特性的试验研究

丁 帅，孟庆龙，王博闻，谢安生，赵 凡

(长安大学 旱区地下水文与生态效应教育部重点实验室，陕西西安 710054)

为了解变风量系统静压控制过程，促使变风量空调运行更加稳定，本文参考水系统的水力特性，研究不同位置的末端阀门从开到关，风机频率从大到小的调节下，送风系统主管与支管的静压变化规律。结果表明：被调节支管前一个送风主管段在总送风主管上静压变化最剧烈，主管段静压变化规律与支管推导理论并不吻合；对称支管的静压改变值是否相等，只与被调节阀门位置有关，与风机转速、对称支管阻抗无关；在定管网阻抗，变风机频率时，管网中任意一点的静压值与风机频率呈现二次方抛物线关系。

变风量系统;静压;送风管道;风机频率;末端阀门

1 前言

变风量空调，作为全空气空调系统的一种，相对于风量不变的定风量系统而言，变风量系统可以根据房间负荷的变化调节风机转速，从而改变送入管道中的风量，维持空调区域的温湿度要求，节约风机能源[1]。变风量控制风机转速的主要方式分为3种:变静压控制、定静压控制和总风量控制[2]。前2种控制方式都需要根据送风主管道的静压来调节风机的频率，一般都以自动控制为主导进行，在控制的过程中依赖精准的测量与反馈。造成送风主管道静压变化的原因，一是房间末端VAVBOX的阀门根据房间温度自行调节引起管网阻抗变化[3]，二是为了匹配管道所需静压调节风机频率引起的风机扬程直接变化。

在现实工程当中，变静压的实现难点有以下2点：(1)传感器信号反馈问题；(2)静压稳定值选取问题。前者研究方向为故障研究[4～6]，需要根据大量的经验与统计数据进行故障判断。后者近几年来解决方向有2个：(1)从自控角度出发对控制参数做出优化[7～9]，系统很快能达到稳定，但依赖于传感器和阀门开度的精确反馈；(2)改变静压控制方案，利用前馈—反馈解决提前预测风管压力变化，从而提前调节风机与末端阀门开度，解决了反馈的时滞与震荡问题[10]。无论是哪种方法，反馈还是前馈—反馈的过程中总会给管道静压造成影响，因此研究变风量系统中静压变化规律可以给予判断系统故障方向与选择合适的控制方案以参考。彭红莲与冯萌研究了变风量系统的水力特性[11,12]，但并未提出静压变化规律的原因与不同类型阀门中静压变化的差别。针对上述问题，运用流体输配管网的理论，对风机频率改变或末端风阀开度调节下，送风主管道、支管道中静压值的变化情况进行分析。为设计前期的自动控制的参数选取提供参考，建设后期给系统调试人员加深暖通专业角度上对变风量系统管道静压变化的认知理解，建设完毕后给维护人员提供分析故障或重新调节控制参数的依据。

2 试验对象

2.1 试验平台

试验对象为长安大学市政与暖通试验中心四层的变风量VAV空调系统试验平台，供冷面积106 m2，包含有2个办公室，2个实验室，实验室送风平面图见图1。考虑到不同方位房间与外界换热不同，系统由不同朝向的房间组成，且同一朝向房间面积大小不一。401,406,413房间选用的VAVBOX型号相同，为RSV-TU-1-I-05-L，可用风量范围为0～680 m3/h；405房间的型号为RSV-TU-1-I-07-L，可用风量范围为0～1360 m3/h。系统仅一台组合式空调机组，额定风量为5000 m3/h，机组全静压为300 Pa。

图1 变风量送风系统平面示意

由图1可见，送风主管上共有4个静压测点(测点1～4)，送风支管上的测点有测点5～7，测点4既可以作为送风主管测点，又可以作为401房间支管静压测点，406与413房间支管设计为对称支管，设计风量与支管结构完全相同。定静压的控制原理是在送风管道的某个位置上设置静压传感器，这个位置一般是在送风主管上，距离送风机出口的距离约为2/3送风主管的长度[13，14]。在本系统中，这个点的位置在靠近401房间支管的主管段上，因此，测点3与测点4均设置在最远端的送风主管上。风管总长30.37 m，风机出口端连接一段垂直向上的风管，接入静压箱，送风管长度从静压箱出口开始算起，各个静压测点相对静压箱出口的距离见图1。

数据采集系统中，上位机利用组态王开发人机界面，通过OPC与PLC建立连接，可实现现场所有模拟量和数字量的采集以及现场设备的控制，包括静压传感器所测静压的数据采集。本试验中以1 s为单位采集静压数据，由于风道静压改变的延迟性不大，因此以3 min为采样周期，剔除坏点后以平均值作为最终的静压值。

2.2 各静压测点可信度分析

首先确定每个静压测点的测量精度是否在可接受的范围之内。所有房间阀门全开，风机频率每隔5 Hz测定一次，初始为50 Hz，终止于15 Hz。测量出来的各静压测点的平均值与标准偏差见表1。由图1可知，测点1的位置是静压箱出口，其标准偏差随着风机频率的增大逐渐增大，在50 Hz时甚至达到±10 Pa左右；其余的静压测点无论在哪个频率下，测量标准偏差均在±2 Pa以内。虽然测点1的静压可以直接反应风机出口静压，但波动太大，这种现象可能是由于风机出口处的气流组织并不稳定导致的。在文献[15，16]中，建议用风机出口点作为变静压取点，第一是因为这个点的静压平均值在改变风机工况或改变管网阻抗时，产生的静压差值相对其余各点所产生的值更大，可以提高传送信号质量，第二是该点处于风机出口位置，可以减少传送延迟。但由于其测量的标准偏差比其余的测点大，因此并不建议将风机出口点作为测量静压的选取点。

从测量的精准性考虑，除测点1之外的其余点均可以选为调节风机频率的测量静压的选取点。也证明了该试验平台静压传感器无故障发生，可以进行后续试验操作。

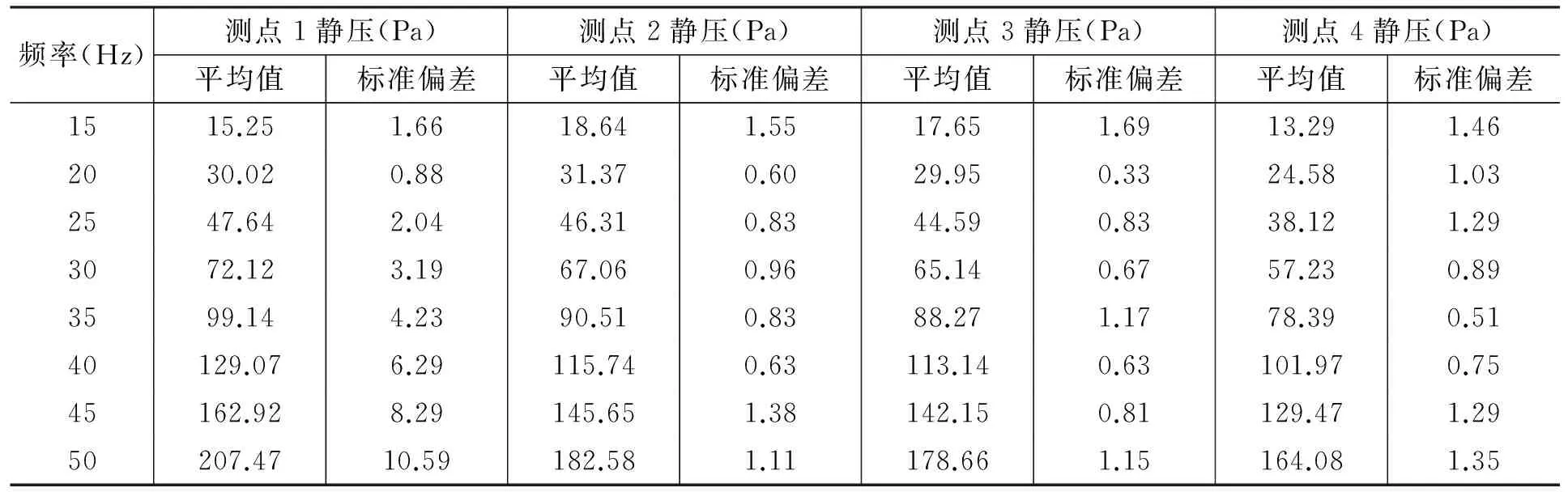
表1 静压测点平均值与标准偏差

3 管网系统水力工况理论分析及试验方案

3.1 水力失调[17]

水系统管网中，管段的实际流量与设计流量的不一致称为水力失调。实际流量与设计流量的比值称为水力失调度，都大于1或都小于1时，称为一致失调，反之，则为不一致失调。水力失调度相等的一致失调称为等比失调，反之称为不等比失调。

3.2 管网系统支管水力工况分析

风系统管网如图2所示。

图2 风系统管网

从流体输配管网水力分析得知：假设阀门C关闭，管网总阻抗增加，总流量减少，此时风机扬程并未改变，因此所有的支路作用压差都会增大，出现一致性失调。支路C后的支管D～N的总作用压差增加，且每个支路的作用压差按相同的比例增大，呈现等比一致性失调，对于支管C前面的支管A和B，呈现不等比一致失调。但理论推导中并未给出管网主管阻抗与流量之间的关系，也未给出对称支管之间的静压变化关系，针对其静压变化规律在试验结果当中进行总结验证。

3.3 试验方案

风机频率为50,40,30,20 Hz时，调节距风机段不同距离的支路阀门开度。保持风机频率不变，调节某个支路末端，保持除被调节阀门以外其余阀门全开(为做对称支管试验，保持413房间VAVBOX阀门开度为50%)。风机初始频率为50 Hz，被调节阀门初始开度为95%，调节单位为5%，调至阀门开度最小后(最小为5%)，重新将被调节阀门打开至95%，更换另一个频率，重复上述步骤，直至4个频率全部完成。更换另一个支路阀门重复上述步骤。模拟在实际的工况中，因为阀门变动或调节风机频率所引起的管道静压变化。

4 试验结果与分析

由于每个频率的试验结果相似，调节以下各阀门时，均以50 Hz为典型工况举例说明，其余频率不再重复赘述。

4.1 调节风机近端房间阀门

调节距风机近端的房间阀门，即406房间，送风主管道测点静压变化情况见图3。

图3 近端阀门调控下送风主管静压的变化

从图3可以看出，406房门阀门开度在5%～25%、80%～95%变化时，各个测点的静压值并无太大变化。这是由于所用VAVBOX的阀门开度特性导致的。该阀门的开度特性为抛物线特性，在开度较小时阀门的流量变化不大，在开度逐渐变大时阀门的流量与阀门两端的压差呈抛物线式上升，在开度达到80%时达到最大，这时即使阀门再开大，流量与压差也几乎不再变化。每改变5%的阀门开度，各测点的静压改变值也是不同的，见图4。横轴为各测点前后阀门开度之差，测点1的差值明显要高于其余3个测点，而其余3个测点的静压差线重叠率很高，即测点2,3,4的静压线在开度为25%～75%时的斜率几乎一致，而测点1的静压在阀门逐渐开大的过程中，静压斜率要比其余各测点大。因此可以判断，主管后3个测点呈现出等比的一致性失调，这与支管的理论推导规律相似。

图4 调节阀门开度产生的静压差值的变化

图5为送风支管的静压变化情况。在406房间阀门开度变化时，406房间支管的测点6静压变化尤其剧烈，其余支管静压斜率一致，与理论推导吻合：调节某个支管其后的其余支管出现等比的一致性失调。413与406房间风管对称分布，但413房间的阀门并未达到全开，因此阻抗与406房间支管并不相同，其测点7的静压也远远高于406房间支管上测点6的静压。

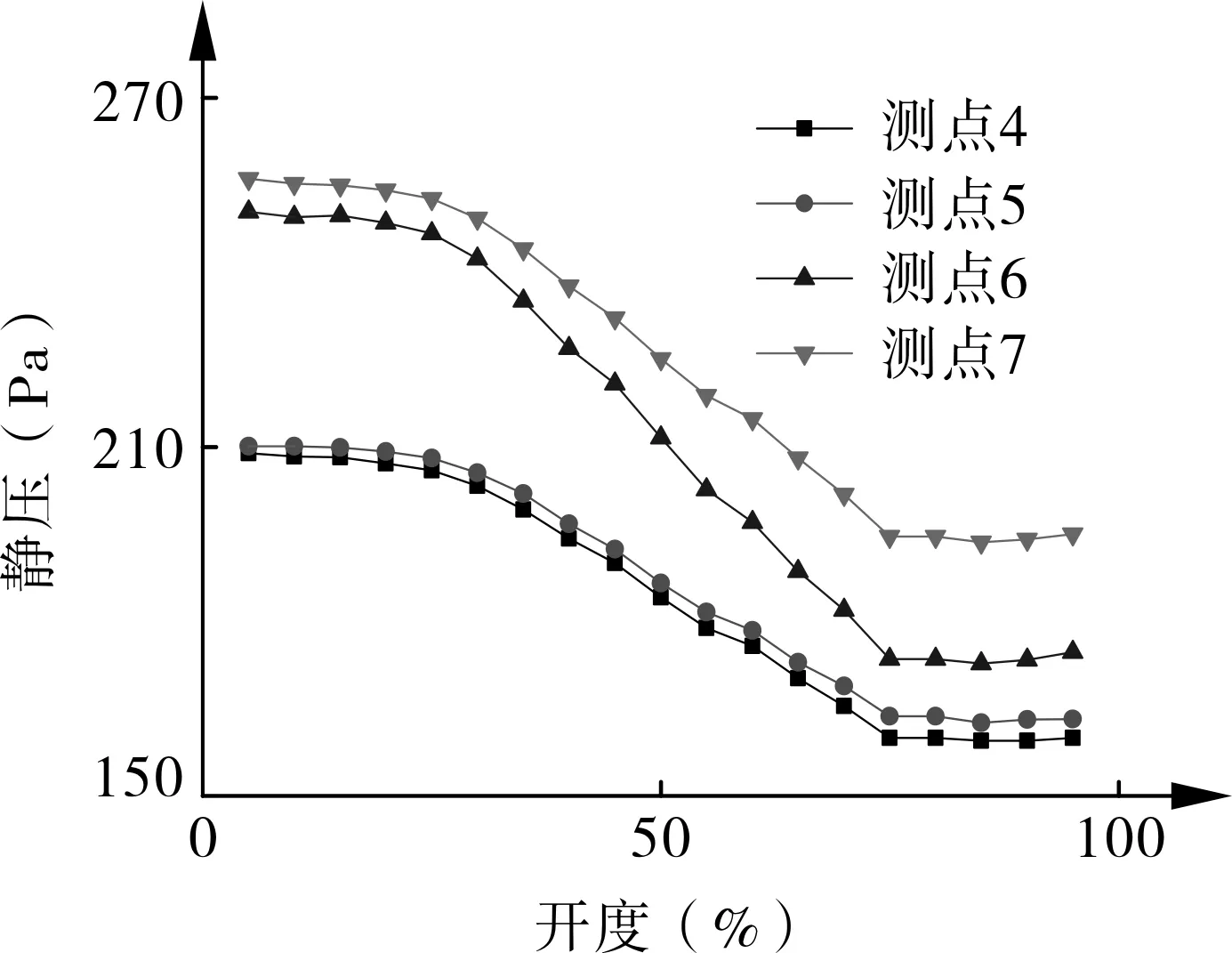
图5 近端阀门调控下送风支管静压的变化

4.2 调节风机中端房间阀门

调节距风机中端的房间阀门，即405房间阀门，送风主管静压结果见图6(a)。从图中静压线的方向与拟合公式看出，测点1,3,4出现一致性失调，405房间支管前一个送风主管的测点2相对于其他主管测点静压变化剧烈。其余测点的拟合公式相似，出现等比的一致性失调，与支管理论推导规律不相符。

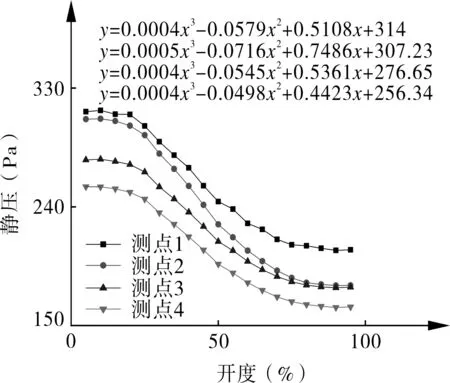
(a) 送风主管

(b) 送风支管

图6(b)为送风支管的静压变化情况。在405房间阀门开度变化时，405支管上测点5的静压变化尤其剧烈，其余支管静压拟合公式各自不同，除对称房间的测点6，7静压拟合公式十分相似，可以看做等比的一致性失调以外，其余支管为不等比一致失调，这与支管理论推导规律吻合。

4.3 调节风机远端房间阀门

调节距风机远端的房间阀门，即401房间阀门，送风主管各测点静压结果见图7(a)。

图7呈现出与上述2个位置的阀门变化时不同的规律，原因在于测点3与测点4在同一个管段上。在远端房间401的阀门从5%～30%变化的过程中，测点3与测点4的静压差别不大，是因为阀门的开度特性在这个过程中并未产生很大的改变，但在开度从40%～80%变化的过程中，由于管道沿程阻力消耗一部分静压，因此测点4的静压比测点3要低。测点2所在管段相当于末端支管前一个送风主管段，在中端阀门(405房间阀门)的变化过程中分析到：某一个支路的阀门开度变化，对紧挨着该支路的送风主管上前一个管道的静压影响，要比其余管道影响大，从拟合的公式可看出，在401房间的阀门开度从35%～80%时，测点2的斜率要比测点1的斜率大。证明了近端与中端阀门改变时所具有的规律，远端阀门也同样适用。由图中拟合的公式可以看出，除测点3与测点4在一个管段上因此出现等比的一致性失调之外，其余测点静压呈现出不等比一致性失调。

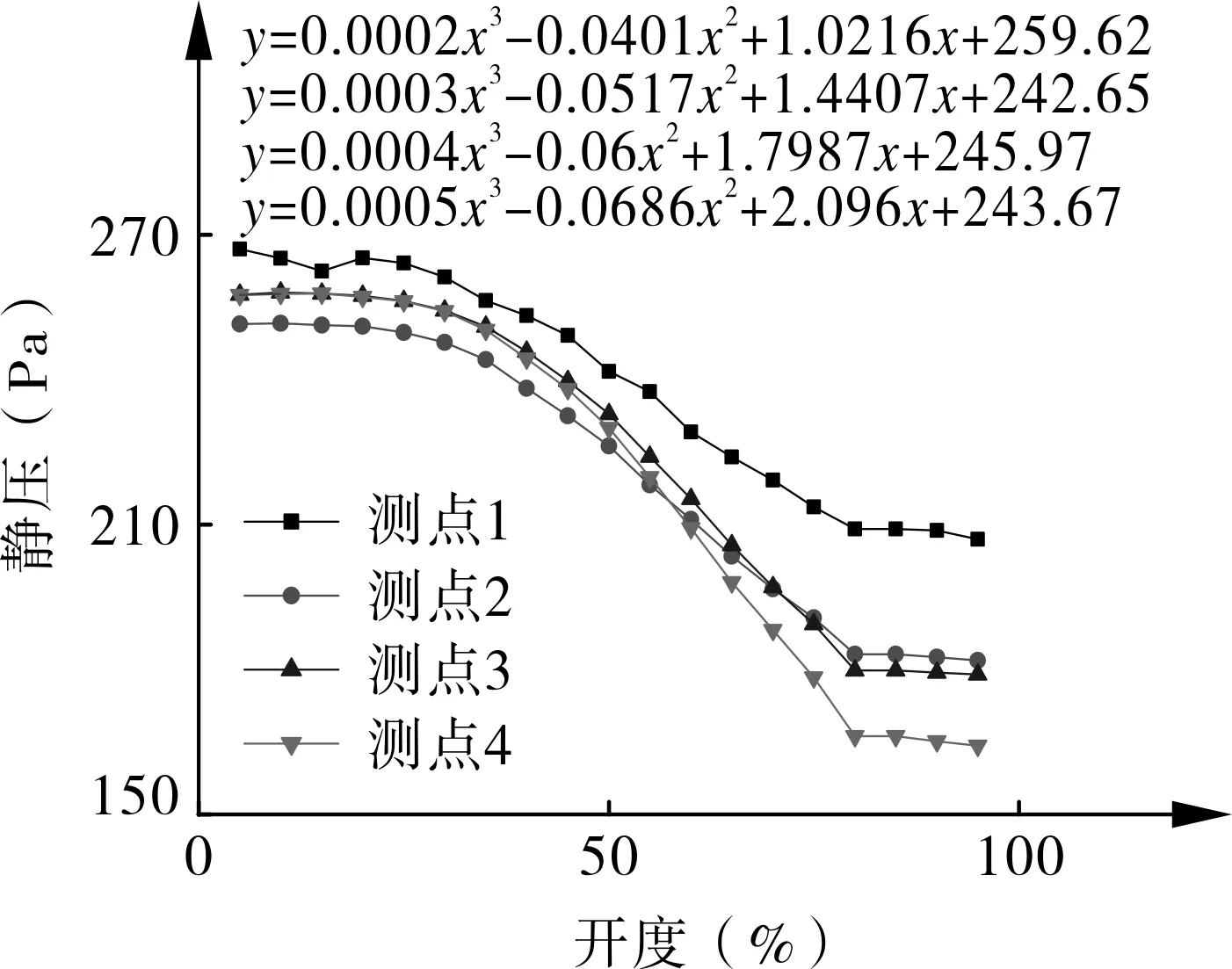
(a) 送风主管

(b) 送风支管

图7(b)为送风支管的静压变化情况。在401房间远端阀门变化时，401房间支管测点4的静压变化尤其剧烈，除406房间支管测点6与413房间支管测点7因为结构对称，静压呈现等比的一致性失调之外，其余支管静压呈现不等比的一致性失调，这与理论分析吻合。

4.4 不同风机频率相同阀门开度下静压结果与分析

在变风量空调系统调节的过程中，在各阀门关闭到最小或开启到最大依旧不能满足房间负荷需求时，应调节风机频率以改变风机扬程，满足各末端需求。试验选取了末端阀门不变的情况下，改变风机频率的管道静压数据进行分析。

图8为远端阀门(401房间支管)开度为60%时，风机频率与各测点静压值的关系图。图中的公式为测点1的静压拟合公式，拟合优度R2≈1，表明在管网阻抗不变的情况下，风机频率与测点静压值呈抛物线关系。其余末端阀门调节时也符合这个规律，不再重复举例。

图8 不同风机频率下测点静压

类比风机在管网系统中的工作状态点，如图9，在管网阻抗S不变、风机频率由n1移动到n2的情况下，风机的工作状态点沿着管网曲线从点A移动到点B。虽然图9的曲线与图8的曲线均表现为抛物线形式，但风机在管网的工作状态点是以全压的方式进行计算与表现的，图8所反应的则是静压的关系图，全压=静压+动压，在动压不确定的情况下，试验证明，静压与全压一样，符合二次方抛物线关系。

图9 风机工作状态点

在管网当中，选取一个管段且假设无漏风。定义该管段初始端的静压值为P0，管段末端静压值为P1，管段内某一点距管段初始端的距离占管段总长的比例为x，该点的静压值为Px。由于管段的横截面不变且无漏风，即管段进口流量与出口流量相等，整个管段的动压不变，沿程阻力的损耗由静压承担，全压损失等于静压损失，即：

P0-Px=ΔP=S0～xQ2

式中S0～x——初始段到该点的管道阻抗

由上式可得：P0=ΔP+Px

在图8中，Px的值在管网阻抗不变的情况下呈二次方抛物线变化。而管网阻抗不变，风机频率变化时，压力与风机频率n平方成正比，即：ΔP=f(n2) ，Px=f(n2)，且两者均为正相关关系，因此可以推断出，P0与频率也呈二次方抛物线变化。管段入口静压与风机出口静压或者局部阻力件的结构有关，因此在知道风机出口静压或局部阻力件对静压分配的情况下，可以推断出管道某一点的静压值。

4.5 对称支管试验结果与分析

上文提到，413房间支管的阻抗比401房间支管大，从图10看出，在调节除406房间以外的其他阀门时，对称支管的测点6与7的静压变化几乎相等，因此可以推断，在不改变风机频率，仅调节除对称阀门本身的其余支管阀门时，对称支管的静压改变值相等，即与调节支管位置有关，与管道阻抗无关。

图10 各频率下各末端阀门从开到关对称支管静压差的变化

图11所示为401房间阀门开度在95%与50%时，改变风机频率，测点6与测点7在不同频率下的静压差的变化。

图11 定阀门开度下改变风机频率时对称支管静压差的变化

从图可见两者并不相等，没有呈现出上述规律。因此对称房间的静压变化值是否相等，只与被调节阀门位置有关，与风机转速无关。

5 结论

(1)末端风阀调节时，送风主管与送风支管静压变化与阀门的开度特性有关。阀门特性为抛物线特性时，测点的静压在5%～25%与80%～95%开度区间内几乎没有变化。主风管静压变化与被调节末端的位置有关，末端调节时，被调节末端所在支风管的前一个送风主管段在总送风主管上静压变化最剧烈，其余送风主管段的测点静压值出现一致性失调，但主管段静压规律并不符合支管静压推导理论；被调节末端所在支管在整个管网的所有支管段中静压变化最剧烈，其余支管静压变化与支管理论规律相吻合。对称支管的静压改变值是否相等，只与被调节阀门位置有关，与风机转速、对称支管阻抗无关。

(2)在风机频率改变，管网阻抗不变时，管网内任何一点的静压值可以根据风机出口静压与局部阻力管件结构所分配的风量计算出来，并且遵循风机工作点的规律，管网内的点也有该点在管网中的工作点，且该点的静压值与风机频率也呈现二次方抛物线关系。

[1] Okochi G S,Yao Y.A review of recent developments and technological advancements of variable-air-volume (VAV) air-conditioning systems[J].Renewable and Sustainable Energy Reviews,2016,59:784-817.

[2] 陈向阳.变风量空调系统的前沿技术[J].暖通空调,2015,45(8):1-10.

[3] 廖丽红.变风量空调系统设计中若干问题的探讨[J].暖通空调,2014,44(8):18-24.

[4] Wang H,Chen Y,Chan C W H,et al.A robust fault detection and diagnosis strategy for pressure-independent VAV terminals of real office buildings[J].Energy and Buildings,2011,43(7):1774-1783.

[5] Du Z,Jin X,Yang X.A robot fault diagnostic tool for flow rate sensors in air dampers and VAV terminals[J].Energy and Buildings,2009,41(3):279-286.

[6] Wang H,Chen Y,Chan C W H,et al.Online model-based fault detection and diagnosis strategy for VAV air handling units[J].Energy and Buildings,2012,55(12):252-263.

[7] 白燕，任庆昌.变风量集中空调变静压广义预测自校正控制与节能技术研究[J].暖通空调，2012,42(12):103-108.

[8] 朱栋华,李肇蕙,田晓曦.蚁群优化控制在变风量空调系统中的应用[J].沈阳建筑大学学报(自然科学版),2012,28(6):1131-1135.

[9] 蒋红梅,李战明,唐伟强,等.变风量空调系统的优化控制研究[J].暖通空调,2016,46(3):84-88.

[10] 刘艳杰,范晓伟,何大四,等.基于预测优化控制的变风量空调系统控制策略的研究[J].中原工学院学报,2015,46(1):71-74.

[11] 彭红莲.压力无关型VAV末端变风量空调系统水力特性研究[D].哈尔滨：哈尔滨工业大学,2008.

[12] 冯萌,李念平,倪吉,等.变风量系统中环状与枝状风道水力特性比较[J].湖南工业大学学报,2007,21(6):15-18.

[13] 武根峰,曹勇.定静压变风量系统静压设定值的确定方法[J].暖通空调,2014,44(7):36-39.

[14] 颜勤伟，丁无极，陈海云，等.基于背压修正的安全阀排量精确计算方法 [J].压力容器，2015,32(6):40-48.

[15] Lorenzetti D M,Norford L K.Pressure setpoint control of adjustable speed fans[J].Journal of solar energy engineering,1994,116(3):158-163.

[16] Steven T Taylor.Increasing efficiency with VAV system static pressure setpoint reset[J].Ashrae Journal,2007,49(6):24-32.

[17] 付祥钊.流体输配管网(第3版)[M].北京：中国建筑工业出版社，2010:171-261.

Experimental Research and Analysis of Static Pressure Regulation in Supply Duct for VAV Air Conditioning System

DING Shuai,MENG Qing-long,WANG Bo-wen,XIE An-sheng,ZHAO Fan

(Key Laboratory of Subsurface Hydrology and Ecological Effects in Arid Region,Ministry of Education，Chang′an University,Xi′an 710054,China)

To understand the process of VAV static pressure control and promote the stability for operation,according to hydraulic characteristics of water system,regulation of static pressure in main and branch pipe of air supply system was researched in experiment by controlling terminal valves in different position from on to off and descending the fan frequency.The results show that the main pipe before the changed branch changes most dramatically.The regulation of static pressure in main pipe does not match the one for branch.Whether or not the static pressure of the symmetric braches are equal depends on the location of changed terminal,not the fan speed or the resistance of symmetric branches.The relationship between static pressure of any point in pipe network and fan frequency is quadratic parabola when the resistance of network is fixed and fan frequency is changed.

VAV;static pressure;air supply duct;fan frequency;terminal valve

1005-0329(2017)01-0066-06

2016-06-22

国家自然科学基金项目(51208059;51508446)；陕西省自然科学基础研究计划(2016JM5076)

TH137;TU831.3

A

10.3969/j.issn.1005-0329.2017.01.012

丁帅(1992-)，女， 在读硕士研究生，主要从事建筑设备自动化方面的研究，E-mail：790843803@qq.com。

孟庆龙(1979-)，男，博士，副教授，硕士生导师，主要从事建筑设备自动化方面的研究，通讯地址：710054 陕西西安市雁塔区南二环中段长安大学环境科学与工程学院，E-mail：mql19@163.com。