刍议苏教版教材集合起始课的思考及调整

顾日新

【摘要】“用教材教”的新课程观既彰显了教材的资源特色，也暗含了教材可变的、发展的、开放的特点.教师应在全面准确把握教材内容的基础上，在不偏离课程标准的前提下，不为教材所束缚，灵活使用教材，积极开发、整合、丰富课程资源，使教材更好地服务于教学，服务于学生.

【关键词】苏教版；集合起始课；例题；习题

【基金项目】教育部人文社会科学研究规划基金项目——我国农村中小学教师的TPACK及其教学表现研究（14YJA880054）；江苏省哲学社会科学一般项目——义务教育均衡发展视域下江苏薄弱学校教师的TPACK状况及其提升路径研究.

教材是课程资源的核心部分，是教师开展教学活动的重要媒介.尽管传统课程观和新型课程观都强调教材的核心地位，但前者“教教材”的思想凸显了教材的权威性，而后者“用教材教”的思想既彰显了教材的资源特色，也暗含了教材是可变的、发展的，也是开放的之特点.新课程观倡导教师不为教材所束缚，在全面准确把握教材内容的基础上，灵活使用教材，积极开发和丰富课程资源.本文是基于苏教版高中数学教材必修1第一章“集合”[1]起始课的教学内容，谈一些粗浅的认识和思考以供借鉴，不当之处，敬请批评指正.

一、“类”是集合的重要特征吗？

苏教版必修1第1章“集合”引言：

蓝蓝的天空中，一群鸟在欢快地飞翔；

茫茫的草原上，一群羊在悠闲地走动；

清清的湖水里，一群鱼在自由地游泳；

……

鸟群、羊群、鱼群……都是“同一类对象汇聚在一起”，这就是本章将要学习的集合.

无论是高声朗读，还是低声慢吟，这段唯美的文字都能给人以一种安谧娴静的意境.但仔细玩味“同一类对象汇聚在一起”这句话，我们不禁要问：“同一类”三个字是集合中元素的重要特征吗？羊群因同类成群而构成集合，那么，草原上羊、牛、狮子、老虎等动物汇集在一起是集合吗？鱼群因同类成群而构成集合，那么，鱼、虾、蟹汇集在一起是集合吗？

关于“类”，石志群教师撰文写到[2]：事实上，将“类”作为集合概念的重要特征的不止斯托利亚尔，著名数学家R·柯朗在其名著《数学是什么》中直截了当地指出：“由对象组成的类或集的概念是数学中最基本的概念之一.”由此可见，“类”的提出是有历史依据的.那么，如何正确理解“同一类”三个字呢？

推敲必修一第5页引入集合定义的方法，笔者认为，“类”的对象是相对的，不是绝对的，如何归类，要看分类的标准是什么.张松年老师认为[3]：苏教版必修1第1章“集合”的章头图是原野上的一群大象.我们可以把象群看作一个整体，其中的每一头象都是这个整体的一个元素；也可以把整个原野系统看作一个整体，其中的每一个物体（一草、一木、一象、一土）都是这个整体的一个元素.正像章首语中所说的，“同一类对象汇集在一起”就成了集合，关键是以什么标准来“分类”，以确定哪些对象“汇集在一起”.

说实话，引言中“同一类”三字确实容易引起初学者对集合元素一般认知上的歧义.为正确理解“类”的内涵，不仅教师自身要对“类”有足够深刻的认识，而且也要让学生弄清楚，这对概念的理解非常必要.

二、“集合”一词的提出到底是哪一年？

苏、沪两个版本的新教材都在正文一侧设置了旁白，创意新颖，有对教材内容作必要补充、提高学生数学认识、拓宽学生数学视野、提升学生数学素养的目的.其中，数学家生平简介是两个版本的共同特色.集合论创始人德国数学家康托尔的生平引起了笔者的兴趣.原文摘录如下（数学家头像省略）：

苏教版必修1第5页

康托尔（G.Cantor，1845—1918），德国数学家、集合论创始人，他于1895年谈到“集合”一词.

沪教版（高一年级第一学期）第5页

康托尔（G.Cantor，1845—1918），德国数学家、集合论创始人.1871年他给集合的说明是：“把一定的并且彼此可以明确识别的事物——这种事物可以是直观的对象，也可以是思维的对象——放在一起，叫作一个集合，这些事物的每一个叫作该集合的一个元素.”

阅读两则旁白，“集合”一词的提出时间分别是1895年和1871年，我们不禁要问：“集合”一词的提出到底是哪一年？查阅文献，关于集合论的诞生有很多记录，主流的说法有三种：

第一种[4]：1873年12月7日，康托尔写信给戴德金，说他已能成功地证明实数的“集体”是不可数的了，这一天也因此成为集合论的诞生日.

第二种[5]：1873年12月7日，康托尔写信给戴德金，说他已能成功地证明实数的“集体”是不可数的，也就是不能同正整数的“集体”一一对应起来.这一天应该看成是集合论的诞生日.

第三种[6]：一般认为，集合论诞生于1873年底.1873年11月29日，康托尔（G.Cantor，1845—1918）在给戴德金（JuliusWilhelmRichardDedekind，1831—1916）的信中提问“正整数集合与实数集合之间能否一一对应起来？”这是一个导致集合论产生的大问题.几天后，康托尔用反证法证明了此问题的否定性结果，“实数是不可数集”，并将这一结果以标题为《关于全体实代数集合的一个性质》的论文发表在德国《克莱尔数学杂志》上，这是“关于无穷集合论的第一篇革命性论文”，在其系列论文中，他首次定义了集合、无穷集合、导集、序数、集合运算等，康托尔的这篇文章标志着集合论的诞生.

从上述三则文献看，尽管“集合”一词的提出没有明确说明是哪一年，但集合论的诞生应该是1873年，那么“集合”一词的提出是19世纪70年代较为客观.

三、Venn图的首次使用是哪一年？

本小节除了以旁白的形式给出集合论创始人康托尔（G.Cantor，1845—1918）的生平简介外，在第6页同样以旁白的形式给出了Venn图的创始人文恩（J.Venn，1834—1923）的生平简介（如下图），但和康托尔（G.Cantor，1845—1918）的简介相比，文字太过简略，以至于Venn图首次使用是哪一年都没有注明.查閱有关文献，关于文恩的个人信息确实非常少.百度百科则引用了《教材完全解读·高一数学必修一》（王后雄主编，中国青年出版社，2014年）关于数学家的简介：1880年，文恩（Venn）在《论命题和推理的图表化和机械化表现》一文中首次采用固定位置的交叉环形式用封闭曲线（内部区域）表示集合及其关系的图形（VennDiagram，也称韦文图或维恩图）.为给学生更多关于Venn图的信息，在原有文字的基础上，加上“Venn图首次使用于1880年”这句话，则显得更为完整.

苏教版必修1第6页

文恩（J.Venn，1834—1923），英国数学家.

四、例题、习题的调整

（一）例题做加法——以固化集合概念的内涵与外延

苏教版教材给出了集合的描述性概念：一般地，一定范围内某些确定的、不同的对象的全体构成一个集合（set）.教學实践中，教师一般在讲授完概念之后会启发学生：从集合描述性概念中，你能得出集合中的元素具有什么性质？学生一般都能顺利地说出“确定性和互异性”.关于集合中元素具有无序性，在讲授完集合相等的概念（如果两个集合所含元素完全相同，那么这两个集合相等）之后，元素的“无序性”也是比较容易得出和理解的.元素的三个性质中，“确定性”比较抽象，若不通过具体的例子对其进行固化.学生是无法形成“确定性”的概念的.所以，可以在原有例题的基础上设计一组题目以加深对集合概念的认识.

如，判断下列各组对象能否构成集合，若能构成集合，指出是有限集还是无限集；若不能构成集合，请你说明理由.

（1）江苏省各地级市；

（2）我们班身高大于1.70米的学生；

（3）末位数是5的自然数；

（4）第一象限内的点.

（二）习题做整合——以突出重点与难点

本课时课后练习由5道题目组成，限于篇幅，不对原文进行摘录（详见教材第7页）：

1，2，4三道题都是集合表示方法的单一应用（一对一的转换），其中，第1题是描述法转换为列举法，第4题的（1）、（2）两小题也是如此；第2题及第4题的第（3）小题则是把文字语言表示的集合用描述法来表示；1，4两题的设置有重复之嫌疑.不如把第1，2，4三题合并为一组题目，以考查学生把自然语言转换为集合语言的灵活性，同时，也能让学生体会到集合表示方法的不唯一性.为突出对集合概念的理解、Venn图的运用及后续学习的需要.在题量保持不变的情况下，对原习题做重新整合，具体如下：

1.试选择适当的方法表示下列集合：

（1）中国国旗的颜色组成的集合；

（2）12的约数组成的集合；

（3）不超过5的自然数组成的集合；

（4）奇数的集合；

（5）偶数的集合；

（6）由方程x2-1=0的所有实数根组成的集合；

（7）不等式x2+1≤0的解集.

（8）平面直角坐标系中第二象限的点组成的集合.

2.教材第3题.

3.数集M={0，x，x2}，那么实数x不能取哪些值？

设计意图：考查集合中元素的互异性.

4.教材第5题.

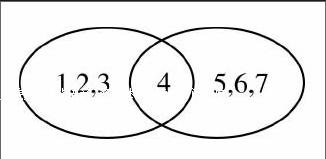
5.如图，Venn图表示哪几个集合？请用适当的方法把所有集合一一表示出来.

设计意图：集合表示方法之间的灵活转换，既为后续学习集合的运算做铺垫，也突出数形结合思想.

总之，在不偏离课程标准的前提下，在尊重教材的基础上，对教材进行思考及合理调整，使教材更好地服务于教学，服务于学生，是我们每一个一线教师的责任.在思考中调整，在调整中前行，也许思考和调整是片面的、狭隘的，甚至是错误的；也许前行的道路是曲折的、艰巨的，甚至是痛苦的.但只要我们不断反思，不断学习，思考和调整的过程一定是美丽的，前行沿途的风景一定是别致的.

【参考文献】

[1]单墫.普通高中课程标准实验教科书·数学[M].南京：江苏教育出版社，2005.

[2]石志群.回归本真深化认识——对“集合”概念教学的思考[J].中国数学教育，2013（6）：2-3.

[3]张松年.寓意深刻匠心独运—例析苏教版高中数学教材的编排结构与设计意图[J].教育研究与评论：课堂观察，2014（4）：22-27.

[4]佚名.集合论[EB/OL].[2014-09-20].http：∥zh.wikipedia.org/wiki/集合论.

[5]佚名.集合论[EB/OL].[2014-09-20].http：∥baike.baidu.com/view/26152.htm？fr=aladdin.

[6]李长杉.集合论与第三次数学危机[J].学周刊，2013（1）：16.