基于模糊物元模型的地表水水质评价

徐继红

(新疆塔里木河流域希尼尔水库管理局，新疆 库尔勒 841000)

基于模糊物元模型的地表水水质评价

徐继红

(新疆塔里木河流域希尼尔水库管理局，新疆 库尔勒 841000)

为解决水质评价中评价指标众多，存在复杂性、模糊性和不确定性等问题，采用基于指标变换值的模糊物元模型对克孜河河流2012年的水质进行评价，并与传统的单因子评价法和灰色关联分析法评价结果进行对比。结果表明：模糊物元评价得出不同时期河流水质级别均为Ⅰ级；基于指标变换值的模糊物元得出的评价结果与灰色关联分析法是一致的，与单因子评价法的评价结果在5月8日的取样值略有不同；基于指标变换值的模糊物元模型应用在该河流水质评价中是合理可行的，且计算简便实用。

模糊物元模型； 指标变换值； 水质评价

水质评价是防治水污染、管理水环境的一项重要的基础性工作，对水资源的可持续发展具有重要意义。目前我国采用的水质评价方法或模型很多，如单因子评价法、内梅罗指数法[1]、六元联系数法[2]、集对分析法[3]、突变理论法[4]、人工神经网络法[5-6]等，这些评价方法都有各自的优点和不足，针对不足，部分学者作出修正并取得了相应的成果。水环境系统是一个多评价指标耦合的动态系统，系统中广泛存在复杂性、模糊性和不确定性等，影响水质评价工作的开展。模糊物元模型是一种在考虑多目标决策的前提下能够很好地处理这几种特性的评价方法，其计算过程中权重的确定特别重要[7]。指标变换值是李祚泳等[8]针对水环境系统中的不确定性问题提出的，将水质评价指标的变换值作为权重进行计算，过程直观、简便。本文选取新疆克孜河河流2012年的水质监测数据，将基于指标变换值的模糊物元模型应用于水质评价，并与单因子评价法和灰色关联分析法进行对比，分析该方法的可行性。

1 基于指标变换值的模糊物元模型

物元分析法是1983年我国学者蔡文创立的，可以解决不相容问题。它的目的在于通过建立的物元模型实现定性到定量的描述和转换，把解决问题的过程形式化，适用于定性、定量相结合的多指标量化问题。物元分析法与模糊理论相结合构成模糊物元模型，可以解决多指标评价过程中的模糊性和不确定性。

1.1 模糊物元模型

设有m个待评价的监测点，每个点有n个评价指标，令xij(i=1，2，…，m；j=1，2，…，n)为第i个点的第j个指标值，建立原始数据矩阵X=(xij)。

a.模糊物元及复合模糊物元。物元分析中将监测点的集合定义为事物M，评价指标的集合定义为特征C，则事物M、特征C和量值x共同组成物元R=(M,C,x)或R=(M,C,C(M))，同时把事物的名称、特征和量值称为物元三要素。如果物元模型中的量值x具有模糊性，便称其为模糊物元。事物M有n个特征C1,C2,…,Cn及其相应的量值x1、x2、…、xn，则称R为n维模糊物元。m(m∈M)个事物的n维物元组合在一起便构成m个事物的n维复合模糊物元R，即

(1)

式中Rmn——m个事物的n个模糊特征的复合物元；

Mi——第i个事物；

Cj——第j个特征。

水质评价指标中，有正向指标和负向指标，正向指标即指标值越大越优型指标，负向指标即指标值越小越优型指标，采用极差变换法计算评价指标的从优隶属度，正向指标公式为

(2)

负向指标公式为

(3)

式中μij——从优隶属度；

maxxij、minxij——为各监测点中每个评价指标的最大值和最小值。

由此可以建立从优隶属度模糊物元：

(4)

b.标准模糊物元和差平方复合模糊物元。标准模糊物元R0n是根据从优隶属度原则，在计算出各评价指标从优隶属度的基础上，根据从优隶属度模糊物元中各评价指标的从优隶属度的最大值或最小值建立的。若以Δij表示标准模糊物元R0n与从优隶属度模糊物元中各项差的平方，则组成差平方复合模糊物元RΔ，即Δij=(μ0j-μij)2，可表示为

(5)

1.2 确定权重

在水质评价中由于各评价指标的重要性不同，对水质的影响也不同，因此在水质评价中应综合考虑各指标的权重，即在评价之前对指标进行赋权。水环境系统中水质指标较多、关系复杂、数据量大，其信息具有高维、非正态和非线性等特征，影响评价结果的诸多指标具有不确定性。针对此问题，李祚泳等[8]依据《地表水环境质量标准》(GB3838—2002)制定了24项地表水质量评价指标的参照值和规范变换式，通过参照值和规范变换式求得各指标的规范值作为权重，这种算法大大简化了水质评价的赋权过程，无须构造众多的评价函数。据此，笔者由选取水质评价指标的参照值和规范变换式计算得到的规范值作为权重。

1.3 贴近度和综合评价

贴近度指被评价样品与标准样品接近的程度，采用欧氏贴近度ρHi作为评价标准，运用模糊算子来计算和构建贴近度复合模糊物元RρH。

(6)

式中ωij——各水质指标在各评价点和水质等级标准中的规范值。

欧氏贴近度ρHi表示第i个评价点与评价标准之间的贴近程度，其值越大表示两者越接近，其值越小表示两者相距越远。从而可以根据贴近度对方案进行优劣排序，也可以根据贴近度进行类别划分。构建出贴近度模糊物元矩阵后，可用各评价点的欧氏贴近度ρHi判断各评价点的水质级别。

2 模型应用

本文以新疆某河流地表水水质监测数据为例(见表1)，利用上述模型进行水质评价。

2.1 模型建立

a.根据实测资料,选择溶解氧(DO，x1)、高锰酸盐指数(CODMn，x2)、化学需氧量(COD，x3)、五日生化需氧量(BOD5，x4)与氨氮(NH3-N，x5)5项指标作为评价因子。以《地表水环境质量标准》(GB 3838—2002)作为水质评价标准，将水质分为五级(见表2)。

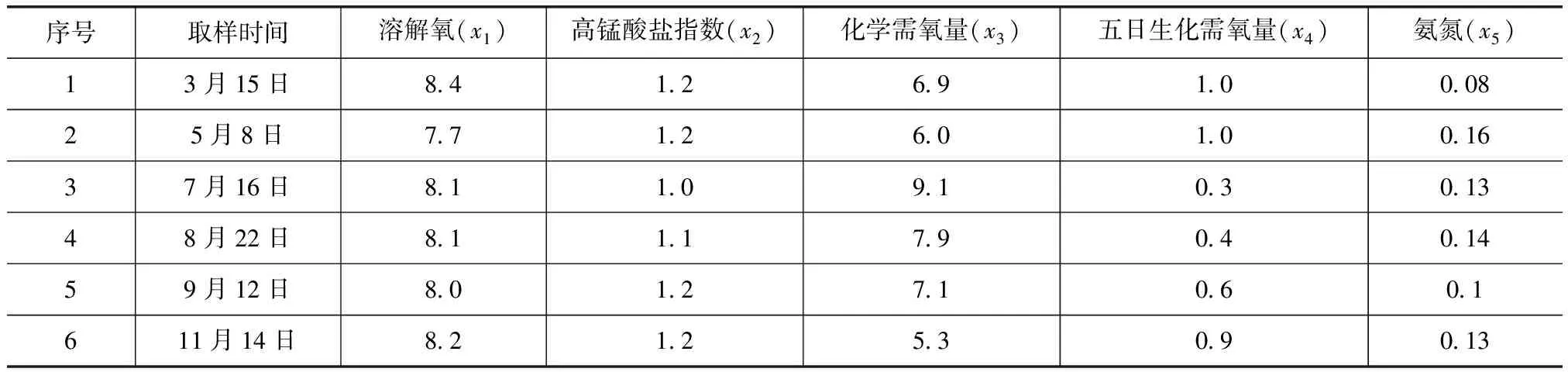
表1 某河流水质监测值 单位：mg/L

表2 地表水环境质量评价标准(GB 3838—2002) 单位：mg/L

b.根据式(2)～式(4)，构建从优隶属度模糊物元(见表3)。

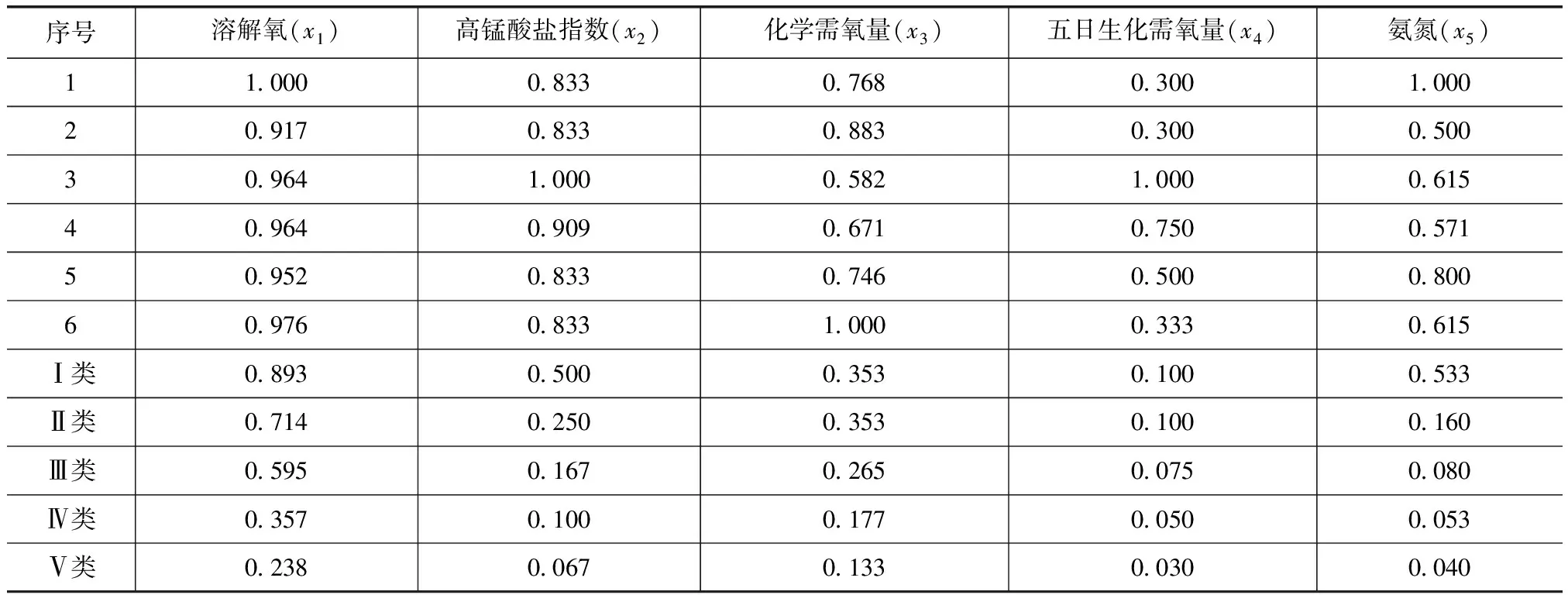
表3 水质评价指标从优隶属度模糊物元

c.根据标准模糊物元，以最大值为最优，计算得差平方复合模糊物元，见表4。

表4 水质评价指标差平方复合模糊物元

d.确定权重。根据文献[8]，确定评价指标溶解氧、高锰酸盐指数、化学需氧量、五日生化需氧量与氨氮的权重分别为0.2586、0.1799、0.1864、0.1715与0.2036。

e.计算贴近度。根据计算得出的贴近度由大到小排列，见表5。根据《地表水环境质量标准》(GB 3838—2002)，与标准贴近度比较可知，6次水质取样，水质级别均为Ⅰ级。

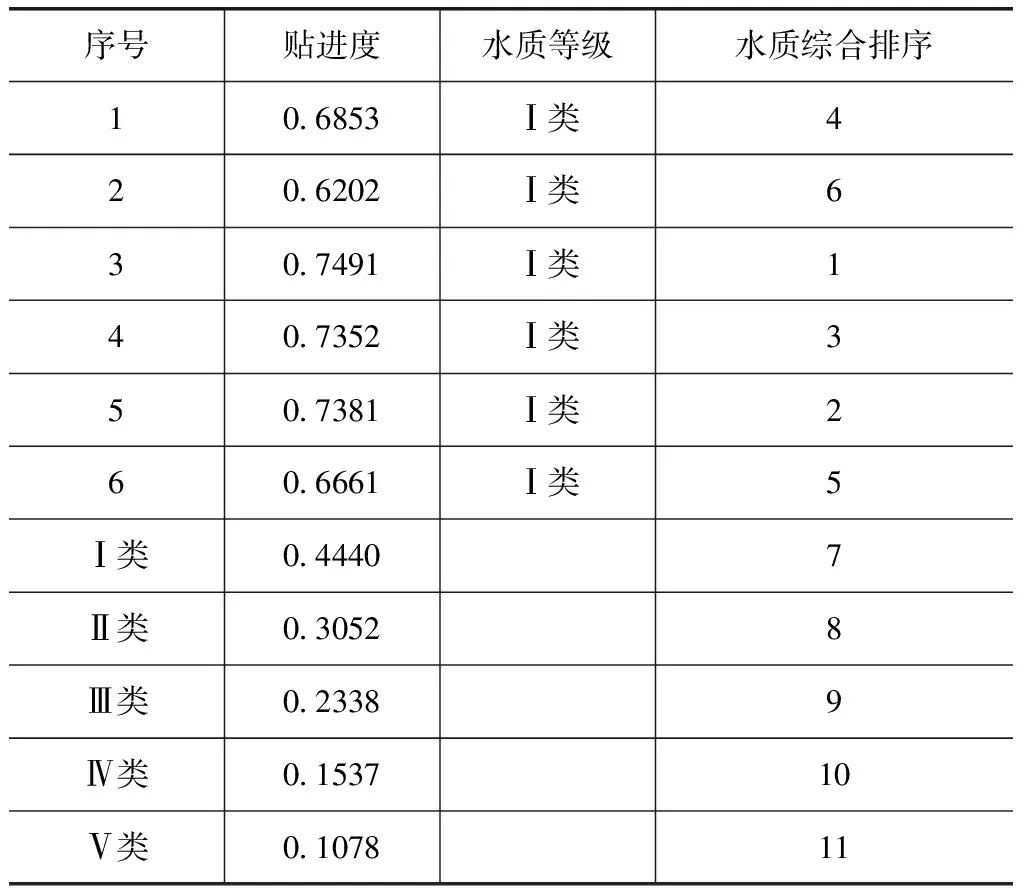
表5 水质综合评价

2.2 结果分析和比较

为了验证基于指标变换值的模糊物元模型的合理性，与传统的单因子评价法和灰色关联分析法评价结果进行对比，见表6。由表6可知，基于指标变换值的模糊物元模型得出的评价结果与灰色关联分析法得出的结果是一致的，与单因子评价法的计算结果在序号2(5月8日)上略有不同，模糊物元模型对该断面的水质评价级别为Ⅰ级，而单因子评价法的为Ⅱ级。实例表明：基于指标变换值的模糊物元模型应用在地表水质评价中是合理可行的，且计算简便实用。

表6 水质评价结果对比

3 结 语

水质评价需要统筹考虑多指标的属性，针对水环境系统中水质指标信息的复杂性和重叠性，将基于指标变换值的模糊物元模型应用于某河流的水质评价中。评价结果表明：该河流不同时期的水质级别均为Ⅰ级。基于指标变换值的模糊物元模型，在权重的计算方面引入指标变换值理论，计算结果更客观，减少了主观性，且计算简便直观，为水质评价提供了一条可行的新途径。但将指标变换值应用于模糊物元模型的权重计算是一种新的尝试，仅为初步研究，尚有很多方面需要进一步探讨。fffffc

[1] 吴彬,减淑英,那晓东.灰色关联分析与内梅罗指数法在克钦湖水体重金属评价中的应用[J].安全与环境学报,2012,12(5):134-137.

[2] 冯莉莉,高军省.基于六元联系数的水质综合评价模型[J].灌溉排水学报,2011,30(1):121-124.

[3] 孟宪萌,胡和平.基于熵权的集对分析模型在水质综合评价中的应用[J].水利学报,2009,40(3):257-262.

[4] 孟晓辰,陶月赞,李晖.基于突变理论的颍河阜颍区段水质评价[J].水电能源科学,2011,29(9):38-41.

[5] Seyam M,Mogheir Y.Application of artificial neural networks model as analytical tool for groundwater salinity[J].Journal of Environmental Protection,2011(1):56-71.

[6] Ioele G,Luca M,Ding E,et al.Artificial neural network combined with principal component analysis for resolution of complex pharmaceutical formulations[J].Pharmaceutical Society of Japan,2011,59(1):35-40.

[7] 张先起,梁川.基于熵权的模糊物元模型在水质综合评价中的应用[J].水利学报,2005,36(9):1-6.

[8] 李祚泳,王文圣,张正健,等.环境信息规范对称与普适性[M].北京:科学出版社,2011.

Evaluation on surface water quality based on fuzzy matter-element model

XU Jihong

(XinjiangTarimRiverBasinNeilReservoirAdministration,Korla841000,China)

Fuzzy matter-element model based on index transform values is adopted to evaluate the water quality of one river in 2012 in order to solve the problems in water quality evaluation index, such as numerous evaluation index, complexity, fuzziness, uncertainty, etc. The results are compared with evaluation methods by traditional single factor evaluation method and grey relation analysis method. The results show that river water quality grade is I at different stages according to the fuzzy matter-element evaluation. The evaluation results concluded from fuzzy matter-element based on index transform values are consistent with that of grey correlation analysis method. The evaluation results of single factor evaluation method are slightly different according to sampling value on May 8. It is rational and feasible to apply the fuzzy matter-element model based on index transform values in river water quality evaluation, and the calculation is simple and practical.

fuzzy matter-element model; index transform values; water quality evaluation

10.16616/j.cnki.10-1326/TV.2017.02.010

TV211.1

A

2096-0131(2017)02- 0033- 04