集对分析自耦合算法在多属性决策中的应用
2017-03-16陆广地
陆广地
(1. 江苏联合职业技术学院 宿迁经贸分院,江苏 沭阳 223600;2. 宿迁学院 数学系,江苏 宿迁 223800)
集对分析自耦合算法在多属性决策中的应用
陆广地1,2
(1. 江苏联合职业技术学院 宿迁经贸分院,江苏 沭阳 223600;2. 宿迁学院 数学系,江苏 宿迁 223800)
区间数多属性决策是一类不确定性决策。针对同一个区间数多属性决策问题可以从不同角度应用集对分析联系数建模决策这一现象,研究了对同一个区间数多属性决策用联系数采用不同算法得到不同的方案排序问题,在此基础上提出集对分析自耦合算法,并用实例说明这种自耦合算法有助于提高区间数多属性决策的科学性和客观合理性。
区间数;多属性决策;不确定性;集对分析;联系数;自耦合算法
0 引言
多属性决策是一类有广泛应用背景的决策。由于存在种种不确定性,常常难以对决策用属性数据作精确的实数刻画,原先用精确的实数表示的确定性决策就演变成不确定性多属性决策。从数学上说,区间数是一种具有不确定性的实数,随机地在给定的一个区间数内部取一实数作为决策用数据,在逻辑上完全允许。迄今为止,一些学者是对区间数多属性决策中的方案按某种特定的规则作出唯一确定的优劣排序,并建议决策者择优方案作决策[1-8];文献[9-15]研究了同一个区间数多属性决策问题中不同方案在不同条件下的不同排序,以集对分析联系数为工具研究了区间数多属性决策;文献[16]研究了同一区间数多属性决策采用不同的集对分析联系数算法导致不同结果时,如何择优决策的问题。本文借鉴文献[12]的思想,提出集对分析自耦合算法用于区间数多属性决策研究,实例表明了集对分析自耦合算法有一定的实用性和优越性。
1 集对分析及其联系数
1.1 集对
集对是指由一定联系的2个集合组成的对象。设有集合E和集合F,若记E和F组成的对象用H表示,则有
H=(E,F)
(1)
集对的实际模型可以是决策中的2个不同的属性(指标)、同一决策问题中的2种方案排序、系统中的确定性和不确定性、区间数的2个端点、区间数2个端点组成的集与区间数内点组成的集等等。
1.2 集对分析
在一定的问题背景下,分析集对中2个集合的全部关系,并把这些关系分成确定性的关系和不确定性的关系2类,用联系数刻画这2类关系的数量或比例,得到一个集对的特征函数,再对特征函数展开分析或有关数学建模与运算解决给定的问题,这是集对分析的基本思路。
1.3 联系数
联系数是集对分析的特征函数。当集对H中的2个集合E和F的全部关系仅分成确定的关系和不确定的关系两大类且不计关系的权重时,则用
U(H)=A+Bi
(2)
作为集对H的 特征函数。式(2)也称为二元联系数,因其有A,B两个联系分量,A是确定的关系数,B是不确定关系数,i作为B的系数,在[-1,1]中视不同情况取值,即i∈[-1,1],具有不确定性,从而使B表示不确定关系数的内涵得到形式上的外显。
对式(2)作归一化处理时,可令N=A+B,a=A/N,b=B/N
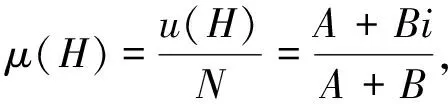
μ(H)=a+bi
(3)
式(3)也称为二元联系度,a为H中2个集合的确定性测度,b为不确定性测度;当给定以确定性测度为参考测度时,a称为(与a的)同一度,简称同一度;b为(与a的)差异度,简称差异度,这时也称式(3)为同异联系度。若把i取值-1的情况单独列出,并用j=-1加以表示,则由式(3)得
μ(H)=a+bi+cj
(4)
式(4)为同异反联系度,或3元联系度,其中a+b+c=1,c称为与a性质相反的对立度。
1.4 联系数的运算
对于2个或2个以上联系数,可以进行普通的加减、乘除、方幂和开方运算,为简明不一一加以说明。
2 集对分析自耦合算法
2.1 联系数的伴随函数
联系数是一种结构函数,携带着相应的结构信息,联系数的伴随函数就是这种结构信息的数学表达,由文献[9-16]可知,目前常用的联系数伴随函数有:
(1) 势函数
设μ为联系数,则势函数记为Shi(μ),其定义为一个联系数的首项与末项之比。
对于二元联系数
μ=a+bi,Shi(μ)=a/b
(5)
对于三元联系数
μ=a+bi+cj,Shi(μ)=a/c
(6)
(2) 相互作用函数
设μ为联系数,则其相互作用函数记为In(μ),其定义
对于二元联系数
μ=a+bi,In(μ)=ab
(7)
对于三元联系数
μ=a+bi+cj,In(μ)=abi+bicj
(8)
(3) 偏联系数
设μ为联系数,则其偏正联系数记为∂μ,
对于二元联系数
(9)
对于三元联系数
(10)
此外,还有偏负联系数和全偏联系数等概念,因与本文关系不大,这里略过。
(4) 态势函数
设μ为联系数,则其态势函数通常用矩阵表示,对于二元联系数,有
a>b对应同势
(11)
a=b对应均势
(12)
a (13) 共有三种状态势(映射结果)。 2.2 自耦合方法 所谓联系数的伴随函数,是指对于同一个联系数中的2个或2个以上联系分量作不同的运算而得到的函数。对于同一个联系数施行不同运算的方法,本文称之为基于集对分析的联系数的自耦合方法,简称为集对分析自耦合方法。与集对分析自耦合方法相对应的是集对分析非自耦合方法,也即是把集对分析与非集对分析方法相结合的综合方法,见文献[17]。 3.1 区间数 定义:设a、b是两个实数,且a x=[x-,x+] (14) 由区间数的定义易知区间数的上、下界有以下性质。 性质1(确定性) 区间数的上、下界确定。 性质2(不确定性) 在给定区间数的内部有无穷多个值可以任意地选取。 区间数的上述2条性质为区间数向联系数的转换提供了客观条件和保证。 3.2 区间数向联系数的转换 鉴于区间数x的内部有无穷多个值x1,x2,…,xn(n→∞),可以任意选取,为此参考概率统计理论,令x的期望值 (15) a与x的上界x+的离差为b,即 b=x+-a (16) 称式(15)-(16)为区间数向联系数的转换公式。 一大学的5个学院S1,S2,S3,S4,S5的教育、科研、服务状况的多属性综合评估问题,各属性数据及其属性权重均为区间数,见表1,其中的教育Q1,科研Q2,服务Q3都是越大越好的效益型属性。试对这5所学院作综合评估和给出优劣排序。 表1 5个学院的属性值与属性权重区间数 第1步 利用式(15)~(16)把表1的属性权重及属性值转换成基于期望的二元联系数,见表2。 表2 5个学院的属性值与属性权重联系数 第2步 将表2中各属性权重计入到各属性值中得到决策矩阵,见表3。 表3 5个学院的综合评估决策矩阵 第3步 运用二元联系数的加法规则和表3的各学院属性值求得各学院的综合评估联系数。 μ(S1)=0.1913+0.0111i μ(S2)=0.2067+0.0139i μ(S3)=0.2047+0.1168i μ(S4)=0.1897+0.0115i μ(S5)=0.1919+0.0113i 第4步 对5个学院作出初排序。 (1)按照μ(Sk)(k=1,2,3,4,5)中同一度最大值排序优劣得 S2(0.2067)>S3(0.2047)>S5(0.1919)>S1(0.1913)>S4(0.1897) (2)对5个学院的μ(Sk)作不确定性分析:为方便计,分别计算当i=0,i=-1,i=1,i=ak/(ak+bk)时,μ(Sk)的值,按值从大到小作出优劣排序,结果在表4中。 (3)分别对5个学院的μ(Sk)求相互作用联系数In(μ(Sk))=akbk,模函数p(μ(Sk))=,势函数Shi(μ(Sk))及偏正联系数∂(μ(Sk)),并按这些伴随函数值的从大到小作方案排序,见表5。 (4) 对5个学院的属性值作加权计算,用关于i的2次幂函数表示,见表6。 记为μ2(Sk),对μ2(Sk)作不确定性分析,分别取i=0,i=1,i=-1计算,结果在表7中。 第5步 对5个学院作出终排序。分别统计对μ1(Sk)和μ2(Sk)不确定性分析(i的不同值)时,每个学院的序数和,见表8。 表4 5个学院μ(Sk)几种不确定性分析及排序 表5 5个学院μ(Sk)按照几种伴随函数值及排序 表6 5个学院计入属性权重后的2次幂属性联系数 表7 对μ2(Sk)中的i直接赋值结果 表8 5个学的μ(Sk)(1次和2次联系数)作不确定性分析时呈现的排序变化 表8汇集了5个学院在μ(Sk)为1次联系数和2次联系数作不确定性分析7种情况下的排序号变化情况,容易看出,5个学院的综合评估为S2>S3>S5>S1>S4是合理的。表9则是按μ(Sk)伴随函数值的大小作排序的序数和。 表9 5个学院基于μ(Sk)伴随函数的排序 表9汇集了5个学院作基于μ(Sk)伴随函数(相互作用函数,模函数,势函数,偏联系数,二次联系数及其不确定性分析)几种情况下的排序号变化情况,容易看出,5个学院的综合评估排序为S2>S3>S5>S1>S4。这一排序与根据表8作出的排序完全相同,尽管各学院的序数和不同。 (1)对于同一个区间数多属性决策问题,可以选择不同的角度应用集对分析联系数建立决策模型,如一次幂的二元联系数决策模型和二次幂的三元联系数决策模型,对模型中的决策用联系数又可以采用不同算法,从而产生不同的方案排序,最终可以借助统计学的思路来确定出最为客观合理的方案排序,确定出最优方案。 (2)在同一个区间数多属性决策问题中所应用到的集对分析方法,是相互联系着的一组方法,它们从不同角度刻画区间数多属性决策属性值与属性权重不确定性。在本质上是自耦合的,因此,称之为是集对分析自耦合方法。 (3)表9显示,S2在基于μ(Sk)伴随函数所作的排序中有2次排在第5位,对照表5可知,分别是在μ(Sk)的势函数Shi(μ(Sk))和偏正联系数?(μ(Sk)=ak/(ak+bk)条件下排在第5位的,这说明,联系数μ的势函数Shi(μ)和偏正联系数?(μ)是刻画联系数中联系分量联系趋势的函数,而不是刻画联系数中联系分量联系状态的函数,所以,联系数的这2个伴随函数不适宜用来作状态评估,而只能做趋势评估。 (4)区间数多属性决策的不确定性说明了区间数多属性决策问题的复杂性。从仅用一种方法把区间数多属性决策问题转换成确定性的决策问题,给出唯一确定的方案排序供决策选用,到集对分析区间数决策的不确定性“客观承认系统分析,定量刻画,具体分析”无疑是认识上的一大进步,这种进步的现实价值在于经不确定性分析后作出的决策将更符合实际,但也有更多的问题需要深入研究,集对分析自耦合方法的提出,显然是这种深入研究的一条可行途径。 从不同角度应用集对分析理论建模,用联系数的不同算法分析和处理同一个区间数多属性决策问题的不确定性,为作出最优决策提供数学保证和决策支撑,在此基础上提出集对分析自耦合方法,其重要性在于把集对分析用于其它领域,其它问题研究中也有参考价值。作为全新的概念,还有待作进一步的深入和系统性研究。 [1] 朱方霞,陈华友. 区间多属性决策问题研究综述[J]. 模糊系统与数学,2013(3): 149-159. [2] 高峰记. 可能度及区间数综合排序[J]. 系统工程理论与实践,2013(8): 131-138. [3] 高峰记,杨文哲. 指标排序条件下的多指标区间决策[J].数学的实践与认识,2014(21): 179-185. [4] 刘万琳,屈春丽. 基于AHP和区间数排序可能度法的工程项目综合评估法研究[J].数学的实践与认识,2014(21): 100-106. [5] 刘健.刘思峰. 属性值为区间数的多属性决策对象排序研究决策[J].中国管理科学,2010(3): 90-94. [6] 王坚强,吴建文. 基于区间灰色不确定语言的多准则决策方法[J].中国管理科学,2010(3): 107-111. [7] 张方伟,王炜,赵德. 一种基于分层法的区间数多属性决策方法及应用[J]. 系统工程理论与实践,2014(11): 2881-2884. [8] 孙海龙,姚卫星. 区间数排序方法评述[J].系统工程学报,2010(3): 304-312. [9] 叶跃祥,糜仲春,王宏宇,等. 一种基于集对分析的区间数多属性决策方法[J]. 系统工程与电子技术,2006(9): 344-1347. [10] 王坚强,龚岚. 基于集对分析的区间概率随机多准则决策方法[J]. 控制与决策,2009(12): 1877-1880. [11] 盛文平,杨明军,王威. 基于联系数的空中目标威胁评估模型[J]. 舰船电子工程,2010(7): 39-41. [12] 谭乐祖,杨明军. 采用区间数的集对分析目标威胁判断模型[J]. 电光与控制,2011(2): 73-76. [13] 刘秀梅,赵克勤. 基于联系数复运算多多属性决策方法及应用[J]. 数学的实践与认识,2008(23): 57-64. [14] 赵克勤. 基于集对分析的不确定性多属性决策模型与算法[J]. 智能系统学报,2010(1): 41-50. [15] 王万军. 一种基于三元联系数的语言区间信息集结方法[J]. 计算机工程与应用,2014(17): 219-222. [16] 刘秀梅,赵克勤. 区间数决策集对分析[M]. 北京:科学出版社,2014. [17] 汪明武,全菊良,周玉良. 集对分析耦合方法与应用[M]. 北京:科学出版社,2014. (责任编辑:孙文彬) Set Pair Analysis from the Coupling Algorithm in the Application of the Interval Number Multiple Attribute Decision Making Lu Guang-di1,2 (1. Suqian Economic and Trade Branch,Joint Vocational and Technical college of Jiangsu, Shuyang Jiangsu 223600, China; 2. Mathematic Department, Suqian College, Suqian Jiangsu 223800, China) The interval number multiple attribute decision making is a kind of uncertainty decision making. The same interval number multiple attribute decision making problems can contact application of set pair analysis from different angles for modeling decision, this phenomenon is studied to the same interval number multiple attribute decision making with contact number using different algorithms to get different ranking problem, based on this, set pair analysis from the coupling algorithm is put forward, and the example is given to illustrate that the coupling algorithm helps to raise the scientific nature of the interval number multiple attribute decision and the objective rationality. interval number; multiple attribute decision making; uncertainty; set pair analysis; contact number; since the coupling algorithm 2016-12-25 江苏省“333”工程基金资助;江苏省高校哲学与社会科学资助课题(2014SJB333);江苏省陶研会“十三五规划”2016年重点课题(JSTY088) 陆广地(1969-),男,江苏沭阳人,副教授,硕士,宿迁学院兼职教授,主要从事管理决策、联系数学、数学教育及数学文化等研究。 C931.1;C A 1009-7961(2017)01-0089-063 区间数向联系数的转换
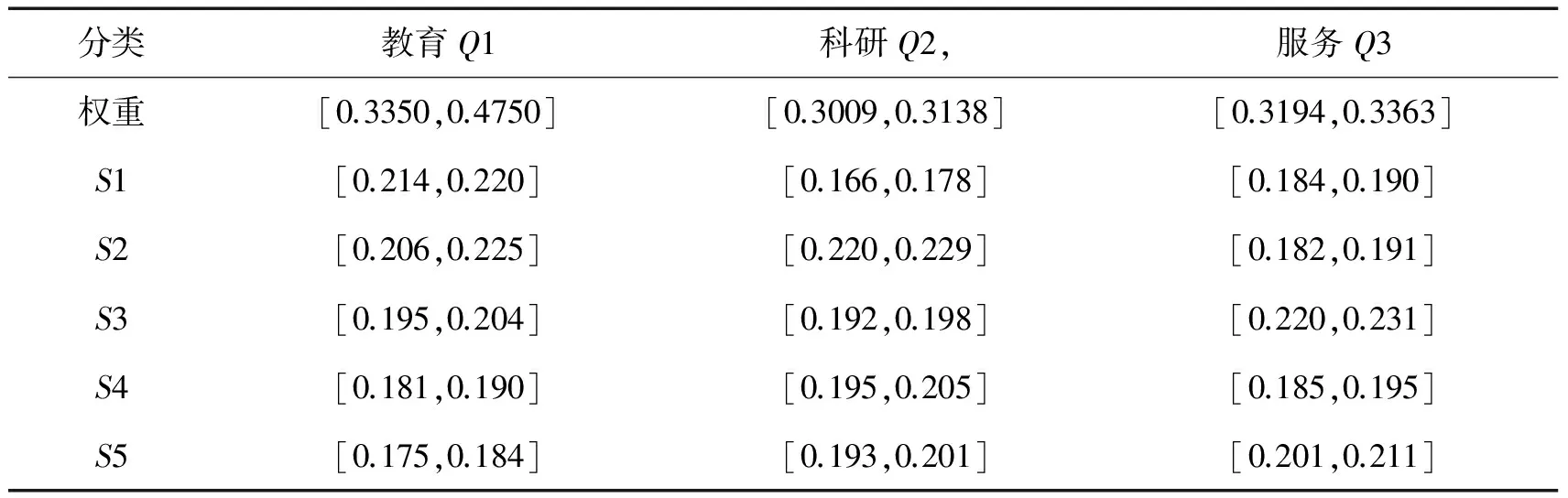
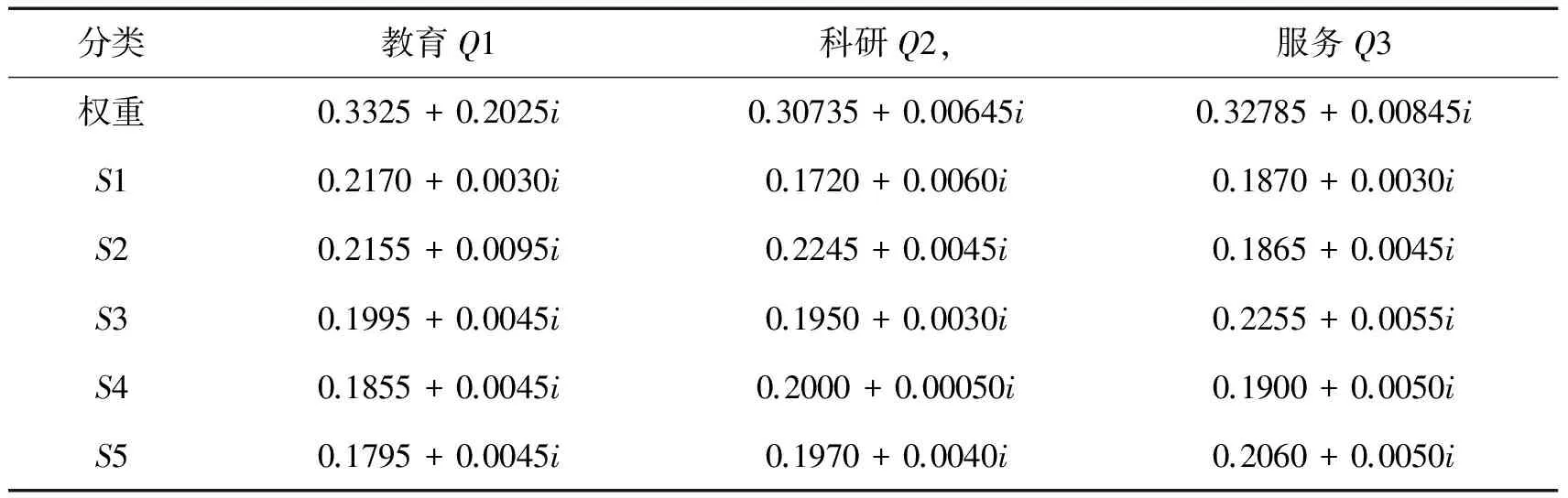
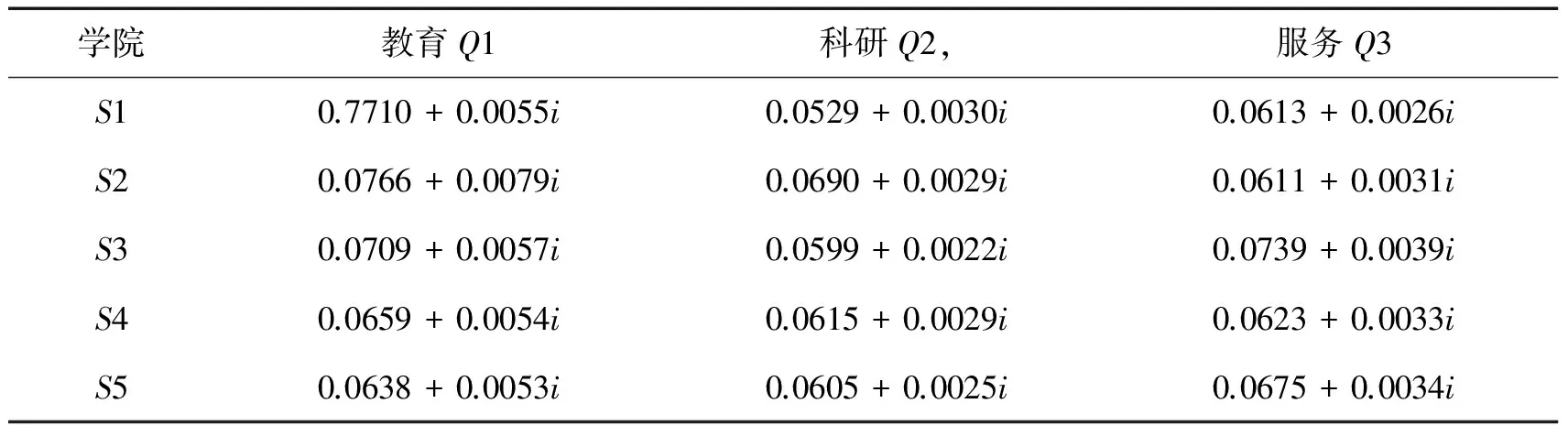
4 应用实例
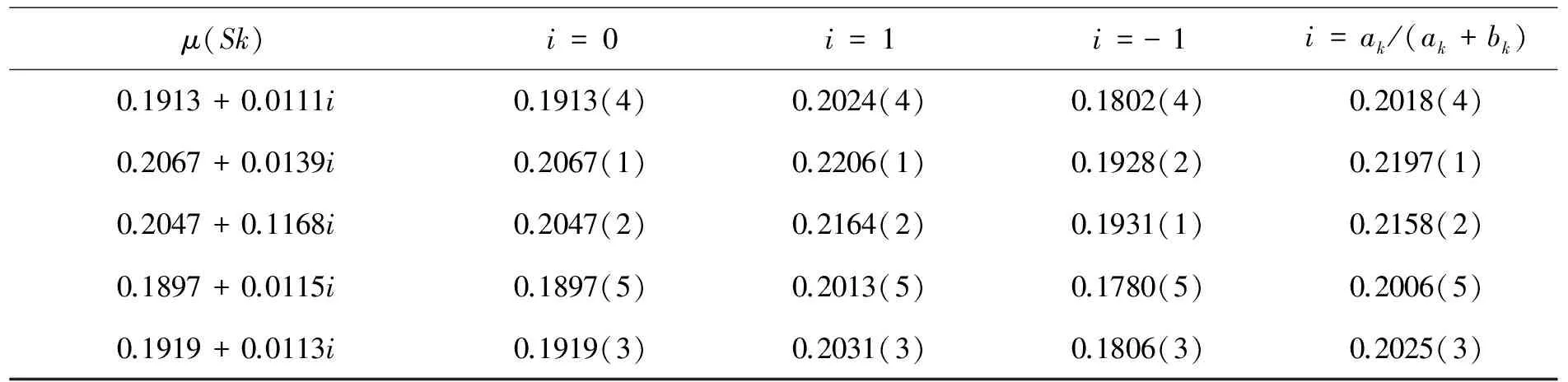
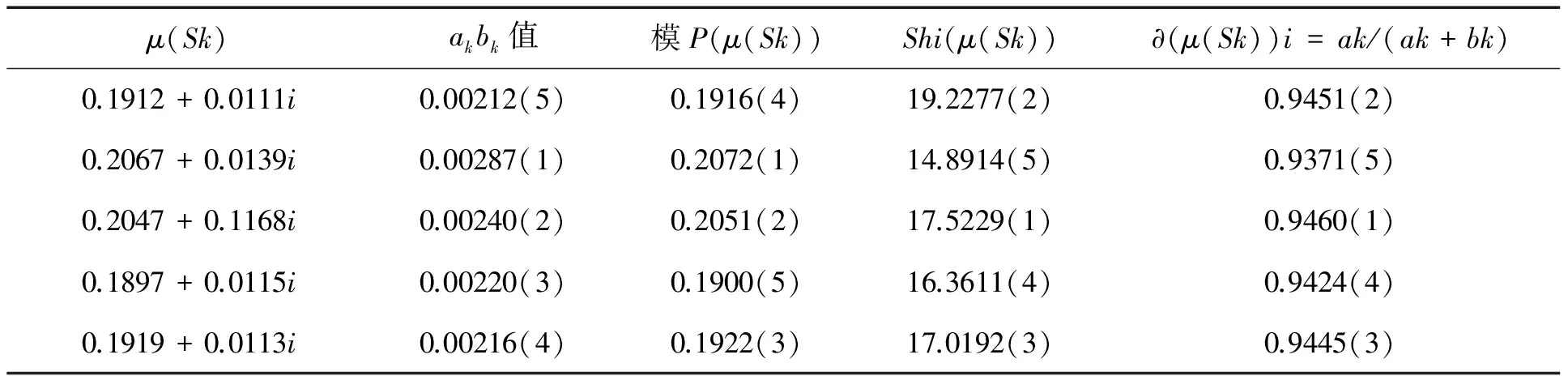
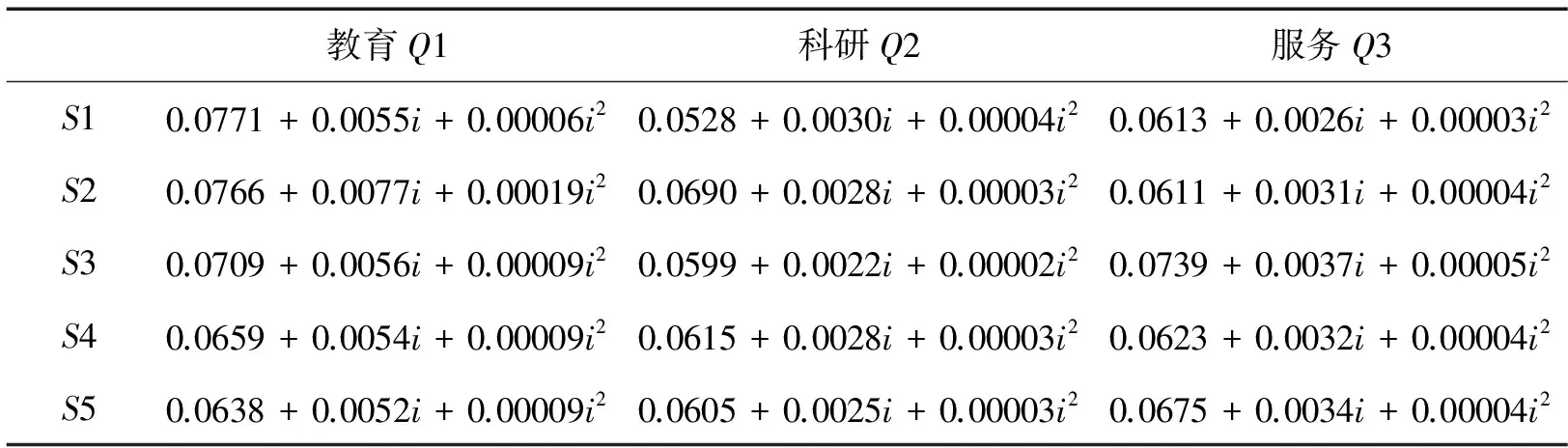


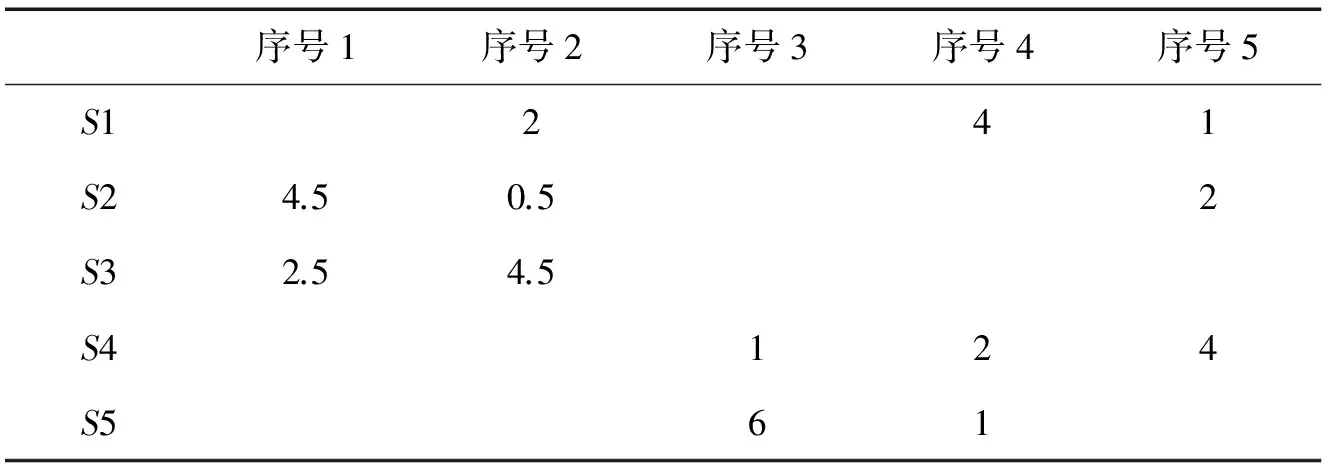
5 讨论
6 结语
