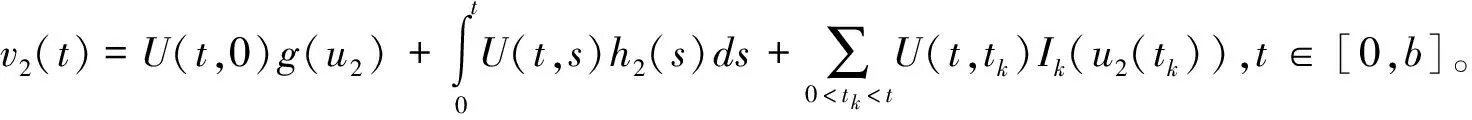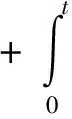一类脉冲积分微分包含的Lipschitz扰动
2017-03-16嵇绍春钱树华
嵇绍春, 钱树华
(淮阴工学院 数理学院,江苏 淮安 223003)
一类脉冲积分微分包含的Lipschitz扰动
嵇绍春, 钱树华
(淮阴工学院 数理学院,江苏 淮安 223003)
利用Nadler不动点定理,讨论了一类具有积分条件和非局部条件的脉冲微分包含问题。本文主要使用多值分析和多值映射不动点定理,在Lipschitz条件下给出微分包含系统解的存在性结论,改进了相关结果。
微分包含;脉冲条件;解的存在性
0 引言
微分方程一般用来描述确定性系统,但在一些经济现象和控制理论中总会存在不确定现象,此时微分包含(也称为多值微分方程)成为研究这类问题的有效模型,见文献[1,2]。近些年,微分包含已发展成多种类型,如发展型微分包含、脉冲型微分包含和中立型微分包含等[3-5],其中文献[5]以非紧性测度为工具,研究了非紧半群条件下脉冲微分包含解的存在性。本文通过多值映射不动点定理,讨论一类具有脉冲条件和非局部条件的积分微分包含在Lipschitz条件下解的存在性。
具体地,在实Banach空间中X讨论如下脉冲微分包含的初值问题:
u'(t)∈A(t)u(t)+F(t,u(t),Gu(t)),t∈[0,b],t≠tk,
△u(tk)=u(tk+0)-u(tk)=Ik(u(tk)),
(1)
u(0)=g(u),


K∈C(D,R+)(从集合D=(t,s)∈R2:0≤s≤t到正实数集R+的连续函数全体)。
1 预备知识

SF(u)={f∈L1([0,b];X):f(t)∈F(t,u(t),Gu(t)),a.e.t∈[0,b]}。
令X,Y是拓扑空间,记P(Y)={A⊆Y:A是非空的},Pkv(Y)={A⊆Y:A是非空的凸闭集}。若算子F的F图graph(F)={(x,y):y∈F(x)}是X×Y的闭子集,则称F是闭算子。
定义1[6]一个双参数算子族{U(t,s),t,s∈△},△={(t,s)∈[0,b]×[0,b]:0≤s≤t≤b},U(t,s):X→X是有界线性算子,如果满足以下两条:
(1)U(s,s)=I,U(t,r)∪(r,s)=U(t,s),其中0≤s≤r≤t≤b;
(2)(t,s)→U(t,s)在△上是强连续的。
则称{U(t,s),t,s∈△}是一个发展系统。
定义2 若函数u∈PC([0,b];X),且满足积分方程
其中f∈SF(u),t∈[0,b],则称u是方程的适度解。
2 主要结果
在算子F,g,Ik是Lipschitz连续的条件下讨论系统(1)的适度解。回顾集合A,B间的Hausdorff距离:
dH(A,B):=max{supa∈Ad(a,B),supb∈Bd(A,b)}。
其中d(a,B)=inf{d(a,b):b∈B},d(A,b)=inf{d(a,b):a∈A}。
作出以下假设:
(H1) 算子A(t)生成一个发展系统{U(t,s),t,s∈△},且supt,s∈△U(t,s)=M。
(H2)F:[0,b]×X×X→Pkv(X)满足
(i)F是Caratheodory上半连续的,即∀x,y∈X,映射F(x,y):[0,b]→Pkv(X)决定一个强可测选择;对a.e.t∈[0,b],集值映射F(t,·,·):X×X→Pkv(X)是上半连续的。且对任意的u,SF(u)是非空的。
(ii) 存在常数l1,l2>0,使得
dH(F(t,x1,y1)),F(t,x2,y2))≤l1‖x1-x2‖+l2‖y1-y2‖。
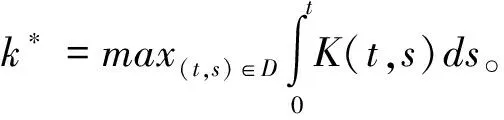
(H4)Ik:X→X是连续函数且存在常数l3>0,使得对任意x,y∈X,k=1,…,m,有‖Ik(x)-Ik(y)‖≤l3‖x-y‖;
(H5)g:PC([0,b];X)连续,且存在l4>0,使得‖g(u)-g(v)‖≤l4‖u-v‖∞,u,v∈PC([0,b];X)。
引理1[7]令X是Banach空间,F是多值映射且满足条件(H2)(i)。设算子Γ:L1([0,b];X)→C([0,b];X)是线性且连续的,则
Γ∘SF:C([0,b];X)→Pkv(C[0,b];X)),
x→Γ∘SF(u):=Γ∘(SF(u)),是空间C([0,b];X)×C([0,b];X)中的闭图算子。
定理1 若假设H1~H5成立, 则脉冲积分微分包含问题(1)在条件
bl1+bl2k*+ml3+l4<1
(2)
成立时, 一定有适度解。

算子K的不动点就是方程(1)的解,下面用Nadler不动点定理证明这一结论。
首先,证明K是闭图算子,且对任意的u∈PC([0,b];X),Ku具有凸闭值。设u∈PC([0,b];X),对任意的v1,v2∈Ku存在f1,f2∈SF(u),使得t∈[0,b]时,
对λ∈[0,1],
由SF(u)是凸集,因此λv1+(1-λ)v2∈Ku,即Ku有凸值。
下面证明K是闭图算子,即graph(K)是闭集。令
(3)
此时,考虑广义的Cauchy算子Γ:L1([0,b];X)→C([0,b];X),
显然Γ是线性且连续的算子。由引理1可知Γ∘SF(·)是闭图算子。因为
vn(·)-U(·,0)g(un)-∑0 且un→u,vn→v,由Γ∘SF(·)是闭图算子可得, v(·)-U(·,0)g(u)-∑0 于是存在f∈SF(u),使得 下面证明K是压缩映射。令u1,u2∈PC([0,b];X),v1∈Ku1,则存在h1∈SF(u1)使得 由假设(H2),(H3), dH(F(t,u1(t),Gu1(t)),F(t,u2(t),Gu2(t)))≤l1‖u1(t)-u2(t)‖+l2‖Gu1(t)-Gu2(t)‖≤(l1l2k*)‖u1-u2‖∞。 再由假设(H2)和选择定理可知,存在可积函数h2∈F(t,u2(t),Gu2(t)),使得 ‖h1(t)-h2(t)‖≤(l1l2k*)‖u1-u2‖∞。 ≤Ml4‖u1u2‖+Mb(l1+l2k*)‖u1-u2‖+mMl3‖u1-u2‖∞ ≤M(bl1bl2k*+ml3+l4)‖u1-u2‖∞ 交换v1,v2的位置,可得 dH(Ku1,Ku2)≤M(bl1+bl2k*+ml3+l4)‖u1-u2‖∞。 根据条件(2)可知K是压缩映射,于是由著名的Nadler不动点定理[8]得到,K有不动点,此不动点就是微分包含问题(1)的解。证明结束。 [1]AubinJP,CellinaA.DifferentialInclusions:Set-valuedmapsandViabilityTheory[M].Berlin-Heidelberg-NewYork-Tokyo:Springer-Verlag,1984. [2]BenchohraM,HendersonJ,NtouyasSK.ImpulsiveDifferentialEquationsandInclusions[M].NewYork:HindawiPublishingCorporation, 2006. [3]CardinaliT,RubbioniP.Ontheexistenceofmildsolutionsofsemilinearevolutiondifferentialinclusions[J].JMathAnalAppl,2005(2):620-635. [4]JiSC,LiG.Existenceresultsforimpulsivedifferentialinclusionswithnonlocalconditions[J].ComputMathAppl, 2011(2):1908-1915. [5] 嵇绍春,李刚.脉冲型算子微分包含解的存在性[J].扬州大学学报:自然科学版, 2015(4):24-27. [6]PazyA.SemigroupsofLinearOperatorsandApplicationstoPartialDifferentialEquations[M].NewYork:Springer-Verlag,1983. [7]ThiemsH.IntegratedsemigroupandintegralsolutionstoabstractCauchyproblem[J].JMathAnalAppl,1990,152:416-447. [8]NadlerNB.Multi-valuedcontractionmappings[J].PacificJMath,1969(2):475-488. (责任编辑:孙文彬) A Class of Impulsive Integro-differential Inclusions with Lipschitz Perturbations JI Shao-chun, QIAN Shu-hua (Faculty of Mathematics and Physics, Huaiyin Institute of Technology, Huai'an Jiangsu 223003, China) By using Nadler's fixed point theorem, a class of impulsive differential inclusions with integral conditions and nonlocal conditions is discussed. The main methods are multivalued analysis and multivalued fixed point theorem. Some existing results of differential inclusions are given under Lipschitz conditions, which extend the existing results. differential inclusions; impulsive conditions; existence of solutions 2016-09-26 江苏省自然科学基金项目(BK20150415);国家自然科学基金项目(11601178) 嵇绍春 (1981- ),男,江苏淮安人,副教授,博士,主要从事非线性分析与泛函分析的研究。 O175.15 A 1009-7961(2017)01-0085-04