关于模糊关系合成运算一个性质的商榷

沈进中，邓留保

(1. 安徽理工大学 电气与信息工程学院，安徽 淮南 232001；2. 安徽财经大学 金融学院，安徽 蚌埠 233030)

关于模糊关系合成运算一个性质的商榷

沈进中1，邓留保2

(1. 安徽理工大学 电气与信息工程学院，安徽 淮南 232001；2. 安徽财经大学 金融学院，安徽 蚌埠 233030)

针对清华大学出版社出版的教材《智能控制基础》，给出的模糊关系合成运算一条性质，经过实例验证，发现该性质并不成立。于是对该问题进行严格的数学分析和推导，得出正确的结论，并将其推广到更一般的情形，同时也表明《智能控制基础》中的部分结论是错误的。最后，举出两个实例，计算结果进一步验证所得出的结论的正确性。

模糊关系；模糊合成；模糊包含

0 引言

在《智能控制基础》[1]的32页，对所给出的模糊关系合成运算性质进行了逐一验证。验证研究发现，无论如何也得不出模糊关系合成对“交运算”满足分配律，于是查阅专著[2]，在专著[2]的33页，其给出的结论与[1]中相同，即模糊关系合成对“算”满足分配律，专著[3-5]没有给出模糊关系合成的运算性质，仅仅给出模糊关系合成的定义。本文就这一问题进行分析。

1 预备知识

定义[1-2]如果R和S分别是笛卡尔空间U×V和V×W上的模糊关系，则R和S的合成是定义在笛卡尔空间U×W上的模糊关系，记为R∘S。其隶属度函数的计算方法如下：

∀(u,w)∈U×W，其对于R∘S的隶属度为

2 主要结论

定理2.1 若R是U×V上模糊关系，S和T是V×W上的模糊关系，则成立

R∘(T∩S)⊆(R∘T)∩(R∘S)

(1)

证明：根据模糊合成运算的定义，∀(u,w)∈U×W，其对于R∘(T∩S)的隶属度为

(u,w)对于(R∘T)∩(R∘S)的隶属度为

显然，有

因此成立

μR∘(T∩S))(u,w)≤μR∘T∩R∘S))(u,w)

这表明

R∘(T∩S)⊆(R∘T)∩(R∘S)

成立，证毕。

定理2.2 若R和T是U×V上模糊关系，S是V×W上的模糊关系，则成立

(R∩T)∘S⊆(R∘S)∩(T∘S)

(2)

证明：∀(u,w)∈U×W，其对于(R∩T)∘S的隶属度为

其对于(R∘S)∩(T∘S)的隶属度为

显然，

μ(R∩T)∘S(u,w)≤μ(R∘S)∩(T∘S)(u,w)

这表明

(R∩T)∘S⊆(R∘S)∩(T∘S)

成立，证毕。

注：在文献[1]和[2]给出的相关结论是

R∘(T∩S=(R∘T)∩(R∘S)

(3)

(R∩T)∘S=(R∘S)∩(T∘S)

(4)

这是显然是不对的，在下面即将给出的反例中，可以很好地验证本文所给的结论的正确性。同时也说明文献[1]和[2]给出的相关结论是不对的。

定理2.1和定理2.2的结论是对两个模糊关系的交运算成立，如果是对多个模糊关系的交做合成，结论是会如何呢？我们有如下定理。

定理2.3 若是U×V上模糊关系，St(t∈T)是V×W上的模糊关系，则成立

(5)

证明：根据模糊集合(关系)相等的定义，只需证明等式(5)中左右两边的两个模糊集合的隶属度函数相等即可。

对任意的v,t,显然成立

即

定理2.4 若Rt(t∈T)是U×V上模糊关系，S是V×W上的模糊关系，则成立

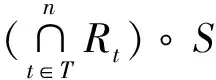
(6)

证明：类似定理2.4，略。

3 反例

例1 已知论域，

可计算得

可见，R∘(T∩S)⊆(R∘T)∩(R∘S)且R∘(T∩S)≠(R∘T)∩(R∘S)。

例2 已知论域U={u1,u2},V={v1,v2},W={w1,w2},

经计算，可得

可见，(R∩T)∘S⊆(R∘S)∩(T∘S)且(R∩T)∘S≠(R∘S)∩(T∘S)。

4 模糊关系合成对交运算成立的条件

一个问题：什么情况下，模糊关系从包含变为模糊相等？即式子(3)、(4)成立，下面将给出两个定理。

定理4.1 若R是U×V上模糊关系，S和T是V×W上的模糊关系，若S⊆T或T⊆S。则成立

R∘(T∩S)=(R∘T)∩(R∘S)

证明：若S⊆T，则(R∘S)⊆(R∘T)，显然成立R∘(T∩S)=(R∘T)∩(R∘S)。同理，若T⊆S，定理4.1结论成立。证毕。

定理4.2 若R和T是U×V上模糊关系，S是V×W上的模糊关系，若R⊆T或T⊆R，则成立

(R∩T)∘S=(R∘S)∩(T∘S)．

证明：类似定理1，略。

5 结语

本文针对文献[1]和[2]中模糊关系合成运算的性质展开了细致讨论，指出了其中一条性质的错误性，并经过严格的数学分析和证明，给出了正确结论，同时以两个实例，验证了本文所得结论的正确性，进一步表明了[1]，[2]中的结论是错误的。本文最后给出两个定理，以此说明在满足一定的条件之下，定理5.1和定理5.2中的模糊包含可以改成模糊相等。

[1] 韦巍,何衍.智能控制基础[M].北京：清华大学出版社,2008.

[2] 黄卫华,方康玲.模糊控制系统及应用[M].北京: 电子工业出版社,2012.

[3] 韩峻峰,李玉惠.模糊控制技术[M].重庆：重庆大学出版社,2003.

[4] 廉小亲.模糊控制技术[M].北京: 中国电力出版社,2003.

[5] 刘金琨.智能控制(第三版)[M] 北京: 电子工业出版社,2014.

[6] 梅加强.数学分析[M].北京: 高等教育出版社, 2011.

(责任编辑：孙文彬)

A Discussion on the Property of Composition of the Fuzzy Relations

SHEN Jin-zhong1, DENG Liu-bao2

(1. College of Electrical and Information Engineering, Anhui University of Science and Technology, Huainan Anhui 232001, China; 2. School of Finance, Anhui University of Financial and Economics, Bengbu Anhui 233030, China)

The monograph Fundamentals of Intelligent Control published by Tsinghua University Press gave a property of composition of the fuzzy relations, however, the author of this article found that this property was not true by calculation from some practical examples. Then the study on this problem is carried out by strict mathematical analysis and derivation, and some new conclusions are obtained, and these new results are extended to a more general case, it shows that some corresponding conclusions are incorrect in Fundamentals of Intelligent Control. In the end, two examples are given to verify that the new results are correct.

fuzzy relations; fuzzy composition; fuzzy inclusion

2016-09-30

安徽省高校自然科学研究重点项目(KJ2015A076); 安徽理工大学硕博基金(ZY022)

沈进中(1985-)，男，湖北黄冈人，讲师，博士，主要从事模糊控制、系统稳定性和非线性系统研究。

TP273

A

1009-7961(2017)01-0038-04