一种一维弹道修正弹自适应落点控制算法
2017-03-16丁翔洲李银伢
丁翔洲,李银伢
(南京理工大学, 南京 210094)
【装备理论与装备技术】
一种一维弹道修正弹自适应落点控制算法
丁翔洲,李银伢
(南京理工大学, 南京 210094)
针对在发射前预先装定弹道信息的传统弹道修正弹控制方法存在易受外界因素扰动的问题,提出了一种一维弹道修正弹自适应落点控制算法;通过建立弹道滤波模型外推弹道,利用自适应落点控制算法,得到阻尼器修正参数修正弹道,并根据弹丸飞行参数每隔特定时间循环上述过程实现自适应修正,直到引信引爆;仿真结果表明:滤波外推后的弹道更接近于实际弹道,经过多次弹道修正可以有效减小落点弹目偏差,与传统弹道修正方法相比较,改进弹道修正方法可较大幅度提高对静态目标的打击精度。
弹道修正弹;弹道滤波;自适应;落点控制;打击精度
弹道修正弹作为一种新型的精确打击弹药,以其低廉的造价,相比常规弹药具有对目标更高的命中概率和毁伤效能而备受各国青睐。
弹道修正弹是利用弹道修正引信对原有榴弹、迫击炮、火箭炮等常规武器发射的常规弹药用引信进行替换,根据弹道修正引信上的探测模块测量得到修正弹的飞行位置、姿态、速度等参数,经由解算模块解算得到修正弹飞行弹道轨迹并与预先装订飞行弹道轨迹进行比较,控制器根据比较差值控制阻尼器修正弹道,使其按照预定弹道打击目标[1]。
一维弹道修正弹是对射程进行修正的修正弹,是弹道修正弹发展的初级阶段,其技术相对简单,易于实现,是目前弹道修正弹发展的主流方向[2]。
由于传统一维弹道修正弹的修正原理是弹丸实测飞行弹道与预先装订弹道对比修正,但是这种修正原理过多依赖于雷达实测飞行弹道参数的精度和预先装订的方案;且在修正过程中仅作一次修正,然而修正弹修正后仍然需要飞行一段时间,则在此阶段外界扰动对修正弹落点产生的干扰无法有效抑制,使落点产生较大偏差。文献[3-4]对弹道修正弹落点预测中通过建立弹道滤波方程,采用扩展卡尔曼滤波方法外推弹道,预测弹丸的落点。但是,其采用的扩展卡尔曼滤波在线性化过程中会引入线性化误差。文献[5]为了研究进一步提高弹箭密集度,对“当前”动态运动线性模型卡尔曼滤波和非线性质点弹道模型的扩展卡尔曼滤波在GPS量测数据下进行了比较,说明了两种弹道滤波模型在不同条件下的优缺点。文献[6]对采用阻力环装置的一维弹道修正弹在弹道不同位置的作用对弹道修正能力的影响进行了数值计算和炮射试验,为一维弹道修正弹的弹道设计提供了依据。文献[7]利用阻力环进行一维弹道修正的能力以及阻力环张开时刻与射程修正量之间的关系,提出了阻力环张开时刻的算法。文献[8]为了简化终端弹道修正弹参数设计,提出了基于自适应惩罚函数的弹道参数优化设计方法,验证了该方法在弹道修正弹的参数设计理论上的优化能力和鲁棒性。
综合上述文献,传统弹道修正弹的弹道修正方法存在着两个问题:采用预先装订弹道方案,过多依赖于雷达实测飞行弹道参数的精度和预先装定的方案,不适用于修正弹根据目标射程自适应修正弹道;采用一次弹道修正,其修正后仍然需要飞行较长一段时间,此阶段无法有效抑制外界扰动对修正弹落点产生的影响,使落点产生较大偏差。
本文针对上述问题提出了两点改进:一是通过采用无迹卡尔曼滤波外推弹道方法代替预装订弹道;二是根据修正弹飞行参数采取多次弹道自适应修正。通过以上两点改进,在消除扩展卡尔曼滤波引入的线性化误差的同时,可以让修正弹在飞行过程中自适应目标射程修正弹道,可以大幅度降低修正后阶段外界扰动对其落点的影响程度,提高修正弹落点控制精度,使修正弹对目标射击具有更高的命中概率。
1 弹道滤波模型
考虑只要解算弹丸的空间位置与速度等参数兼顾弹道修正弹落点推算的快速性、实时性的要求,采用质点弹道方程模型[9]。质点弹道方程表述如下:
(1)
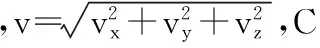
雷达测量方程如下:
(2)
d,β,ε分别为修正弹与发射点的距离,方位角,高低角。
设状态变量
X=(x,y,z,vx,vy,vz)Τ
设观测变量
Z=(d,ε,β)T
则离散状态方程可写为
X(k+1)=f(X(k))*Δt+X(k)+W(k)
(3)
其中,
(4)
量测方程记为
Z(k)=h[X(k)]+V(k)
(5)
W(k),V(k)为零均值高斯白噪声,且分别服从协方差为R,Q的正态分布。
2 无迹卡尔曼滤波解算步骤
为了解决扩展卡尔曼滤波带来的线性化误差问题,本文采用无迹卡尔曼滤波[10]。
无迹卡尔曼滤波步骤:
1) 获得一组采样点及其对应的权值:
2) 计算2n+1个Sigma点集的一步预测
X(i)(k+1|k)=f[k,X(i)(k|k)]
3) 计算系统状态量的一步预测及协方差矩阵

4) 根据一步预测值,再次使用UT变换,产生新的Sigma点集
5) 将由步骤4)产生的Sigma点集代入观测方程,得到预测的观测量
Z(i)(k+1|k)=h[X(i)(k+1|k)]

7) 计算卡尔曼增益矩阵
3 弹道修正弹落点控制算法
已知阻尼器对弹道修正弹的飞行过程中的受力变化等效为弹道修正弹的弹形系数与阻尼器增阻系数的乘积的变化,以下称此二者的乘积值为等效弹形系数。等效弹形系数减小,实现弹道修正弹的正向修正;等效弹形系数增大,实现弹道修正弹的反向修正。
弹道修正弹自适应落点控制算法流程如下(图1):

图1 弹道修正弹自适应落点控制算法流程
1) 雷达跟踪修正弹一段时间后,得到一组修正弹的弹道轨迹诸元参数,滤波外推弹道,估计修正弹的落点。
2) 根据得到的预测落点,估计弹目偏差距离。
3) 在等效弹形系数的变化范围内,根据修正弹飞行参数每隔一定步长进行迭代计算,求取最小弹目偏差距离。
4) 依据得到最小弹目偏差距离对应的等效弹形系数控制阻尼器对弹道进行修正。
5) 弹道修正后,根据飞行参数设定特定的时间重复步骤(1)。
6) 若在飞行过程中,探测模块探测到修正弹进入引信引爆位置,则引爆修正弹。
4 仿真实验
已知某型号修正弹,初速1 000 m/s,射角45°,弹形系数0.6,质量10 kg,弹径100 mm,等效弹形系数变化范围为0.4~0.8,风速扰动为均值5 m/s呈正态分布。每30 s修正弹道1次。目标在31 km处。
图2为在上述发射初始条件下,t=0 s时等效弹形系数的变化对射程修正的影响曲线。

图2 初始时刻等效弹形系数对射程修正量的影响曲线
图3给出了等效弹形系数为0.4~0.8,其射程修正量随修正时刻的变化曲线。
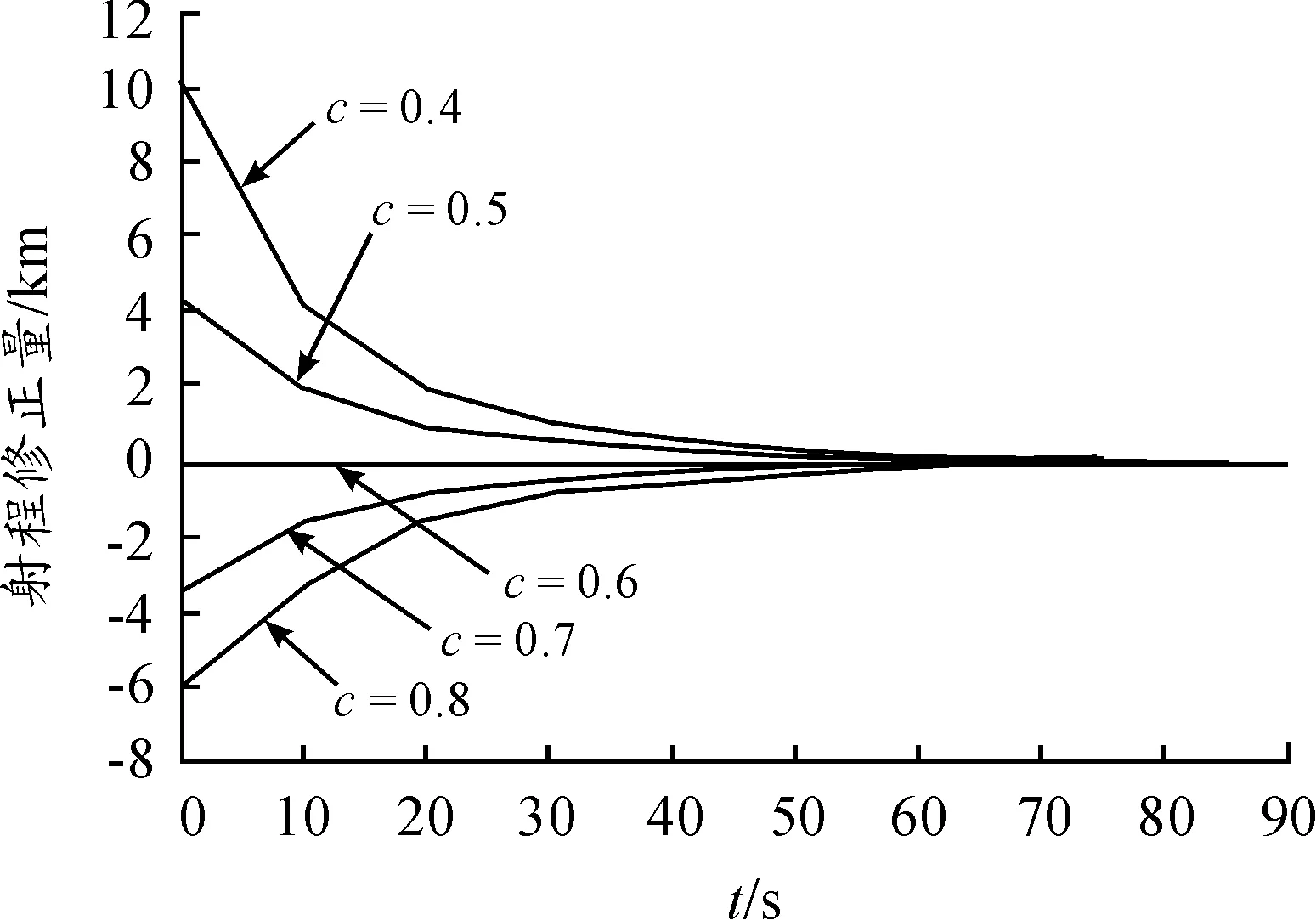
图3 射程修正量随修正时刻的变化曲线
图4给出了一次弹道修正弹道轨迹变化;图5、图6分别为飞行30 s后一次修正的外弹道轨迹的实际值、测量值,以及滤波值所描绘的一段外弹道轨迹和雷达量测误差与滤波后的误差对比。

图4 一次弹道修正弹道轨迹变化
图4说明了修正弹弹道经过一次修正后,落点精度得到大幅度提高。图5、图6说明了通过无迹卡尔曼滤波可以有效抑制雷达噪声对修正弹落点位置预测的干扰。经过滤波后的弹道,比雷达量测值更接近于实际弹道。

图5 一次弹道修正各值变化

图6 一次修正测量误差与滤波后误差
图7给出了二次弹道修正外弹道轨迹变化; 图8、图9分别为飞行60 s后,两次修正弹道轨迹的真实值、测量值与滤波值描绘的弹道轨迹图和测量误差与滤波误差对比图。

图7 二次弹道修正轨迹变化
图7说明与一次弹道修正相比,经过二次弹道修正后的落点位置更接近于目标位置。图8、图9说明了无迹卡尔曼滤波有效抑制了噪声带来的干扰,滤波误差相比于量测误差明显下降。
表1中数据是在上述初速,射角条件下,对距离31 km静态目标射击,仿真10次,传统弹道修正方法(采用EKF滤波,一次弹道修正)与本文改进弹道修正方法(采用UKF滤波,二次弹道修正)的落点弹目偏差距离。

图8 二次弹道修正各值变化
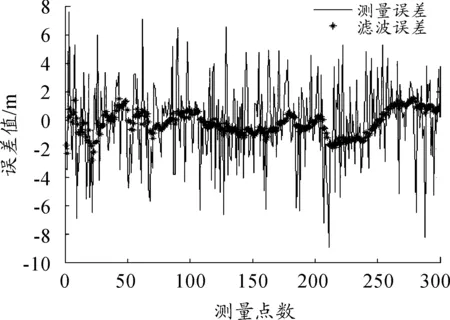
图9 两次修正测量误差与滤波后误差

m
表1的数据表明:在对静态目标射击时,改进后的弹道修正方法在控制修正弹落点精度上比传统方法明显提高。
5 结论
实验结果表明:等效弹形系数的改变越大,修正时间越长,弹道修正的程度越大。通过采用弹道滤波外推和多次弹道自适应修正对传统修正方法进行改进后,在减小修正弹落点弹目偏差距离,提高命中概率方面具有明显的效果。通过减小循环时间,增大修正次数可以进一步提高弹丸落点精度,并可以在一定程度上对慢速(速度在0 但是,随着迭代次数的增加,由于雷达本身存在测量误差以及其他不可消除误差的影响,弹目偏差距离的减小趋势变缓,解算时间明显增加。有待解决寻求射击精度与迭代次数的最佳匹配,以及实现弹道二维修正使其具有二维打击能力。 [1] 张民权,刘东方,王冬梅,庞艳珂.弹道修正弹发展综述[J].兵工学报,2010,31(2):127-130. [2] 赵金强,龙飞,孙航.弹道修正弹综述[J].制导与引信,2005,26(4):16-19. [3] 史金光,徐明友,王中原,张冰凌.卡尔曼滤波在弹道修正弹落点推算中的应用[J].弹道学报,2008,20(3):41-43. [4] 史金光,刘猛,曹成壮,王中原.弹道修正弹落点预报研究[J].弹道学报,2014,26(2):29-33. [5] 李岩,任睿,王旭刚.两种卡尔曼滤波模型在修正弹弹道数据处理中的应用比较[J].弹道学报,2011,23(1):27-30. [6] 王中原,史金光.一维弹道修正弹气动布局与修正能力研究[J].南京理工大学学报(自然科学版),2008,32(3):333-336. [7] 陶陶,王海川.一维弹道修正弹阻力环修正控制算法研究[J].指挥控制与仿真,2009,31(3):88-90. [8] WANG Gang,LI Chenming,LIU Yixin.A new method of optimal design on terminal trajectory correction projectile[C]//Signal Processing,Communication and Computing (ICSPCC),2013 IEEE International Conference on,2013. [9] 韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2014. [10]黄小平,王岩.卡尔曼滤波原理及应用:Matlab仿真[M].北京:电子工业出版社,2015. [11]张丽艳,杜忠华,张志安,等.一维弹道修正弹分段解算控制算法的研究[J].火力与指挥控制,2015(8):143-145. (责任编辑 周江川) One Dimensional Trajectory Correctional Projectile Self-Adaptive Impact Point Control Algorithm DING Xiang-zhou,LI Yin-ya (Nanjing University of Science and Technology, Nanjing 210094, China) In view of the traditional trajectory correctional projectile loading trajectory information before launch was easy to be disturbed by external factors, this paper put forward an one dimensional trajectory correctional projectile self-adaptive impact point control algorithm. Through establishing the ballistic filter model extrapolated trajectory and using the self-adaptive impact point control algorithm, we got the trajectory correctional parameters to modify the trajectory. Based on the flight parameters of the projectile, we cycled the above processes at a specified time to realize the self-adaptive correction until the fuse is detonated. Simulation results show that the trajectory after filter is more close to the actual trajectory, and it can reduce the impact of projectile target deviation effectively by several times of trajectory correction. Compared with the traditional trajectory correctional method, the improved trajectory correctional method has a greater improvement in the precision of the static target. trajectory correction projectile; ballistic filter; self-adaption; impact point control; attack precision 2016-09-11; 2016-10-25 国家自然科学基金项目(61273067) 丁翔洲(1991—),男,硕士研究生,主要从事武器制导研究。 10.11809/scbgxb2017.02.012 丁翔洲,李银伢.一种一维弹道修正弹自适应落点控制算法[J].兵器装备工程学报,2017(2):48-52. format:DING Xiang-zhou,LI Yin-ya.One Dimensional Trajectory Correctional Projectile Self-Adaptive Impact Point Control Algorithm[J].Journal of Ordnance Equipment Engineering,2017(2):48-52. TJ41 A 2096-2304(2017)02-0048-05
