混合粒子群OIF—Elman神经网络系统辨识

黄伟+谢威+付家兴

摘 要：本文提出了一种基于混合粒子群优化算法的OIF-Elman递归神经网络辨识方法。混合算法融合了粒子群算法与差分进化算法的优化能力并加入了在群体最优位置附近的高斯变异操作。与三种典型差分进化算法的仿真对比结果说明了，通过以上改进加快了算法的收敛速度，提高了优化精度。将该辨识方法用于实验室加热炉换热器系统双入双出耦合对象的辨识中，获得的对象模型较之标准的Elman神经网络辨识精度更高，且结果表明本方法与采用反向传播算法作为学习算法的OIF-Elman模型相比，基于改进粒子群算法优化的模型具有更高的精度和更简单的网络结构。

关键词：差分进化；粒子群；高斯变异；OIF-Elman；系统辨识

DOI：10.16640/j.cnki.37-1222/t.2017.05.119

1 概述

神经网络因具有强大的并行处理能力、自组织和自学习能力、非线性映射能力，在系统辨识领域受到了广泛的重视[1]。采用神经网络对系统进行辨识时，无需知道系统的具体结构，通过对相关数据进行训练可以得到辨识模型的网络结构，使得辨识更加简便易行，且可用于闭环辨识。在工程实际中，辨识对象大多为动态系统，且具有较强的非线性，一般的静态前馈神经网络虽然可以采用增加外部迟延的方法辨识动态系统，但会使网络结构复杂化，导致收敛速度变慢。具有内部反馈结构的递归神经网络，因自身具有反馈结构，网络本身便是一个非线性动态系统，成为辨识动态系统的有效方法之一[2]。本文在OIF-Elman[3]递归网络模型的基础上，结合改进的粒子群算法对其进行优化，并用于加热炉换热器对象的辨识，辨识的结果证实了该方法的可行性和优越性。

2 OIF-ELman神经网络

2.1 OIF-Elman网络结构

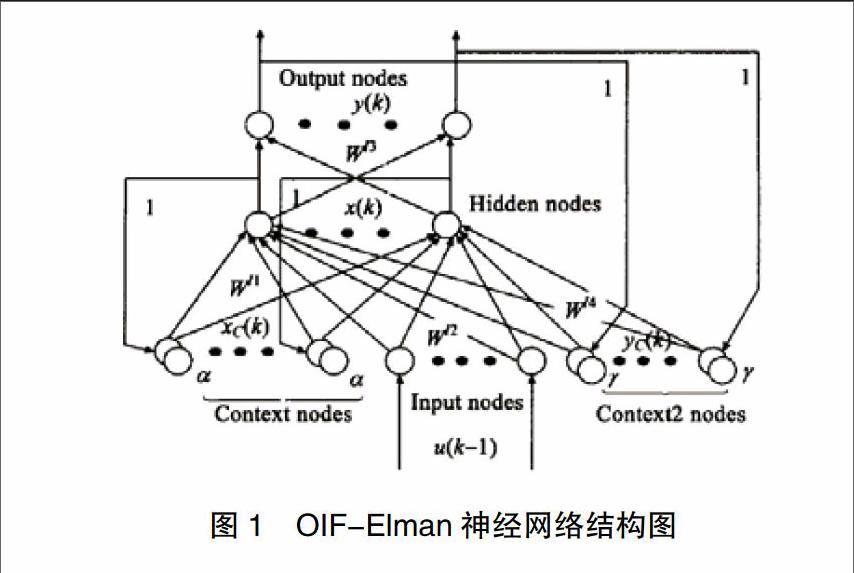
基本的Elman神经网络在BP神经网络基础上加入了局部反馈链接和局部递归单元，具有了动态系统的结构。OIF-Elman网络在Elman网络的基础上增加了输出层节点的反馈，强化了对动态系统的拟合能力，被称为具有输出-输入反馈机制的改进Elman网络[4]。其结构图如图1所示，网络的两个关联层的表达式分别为[5]：

，

2.2 OIF-Elman网络动态系统仿真

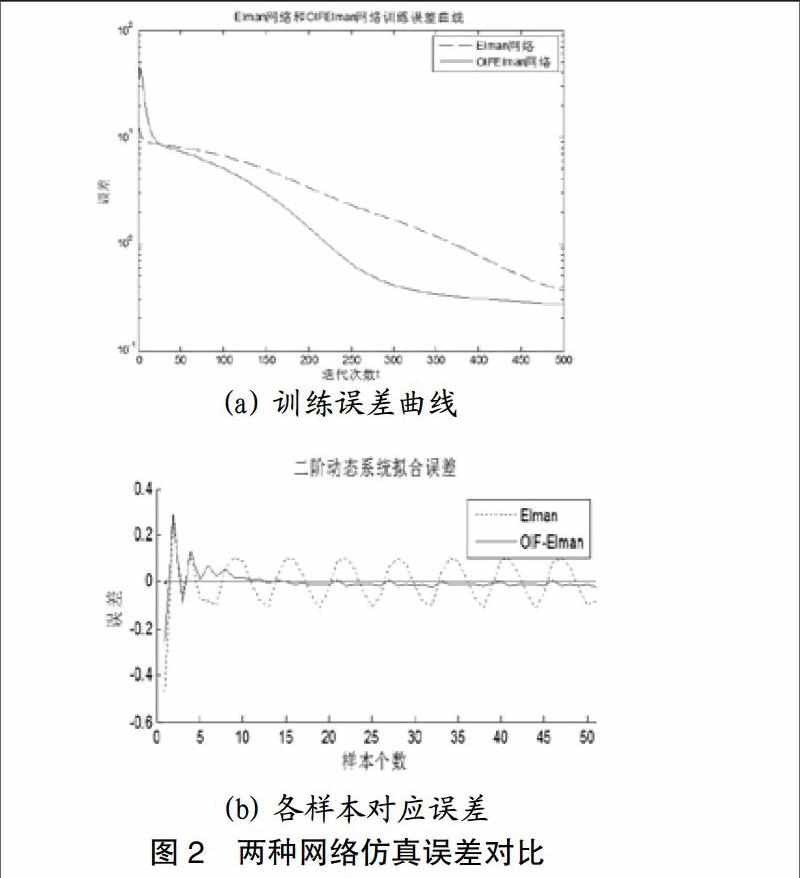
分别采用Elman网络及OIF-Elman网络对二阶动态系统：，输入信号为，取样本个数为50。学习算法均采用误差反向传播（BP）学习算法并比较两种网络的拟合精度，如图2所示。图2（a）為两种网络的训练误差曲线，图2（b）为两种网络输出对应每一个样本的误差，可见OIF-Elman网络相比于Elman网络误差更小，精度更高，在动态系统辨识上更加有效。

3 混合粒子群优化算法

由于传统的BP学习算法收敛速度慢易陷入局部最优等缺陷，本文提出一种改进的混合粒子群优化算法作为OIF-Elman神经网络的学习算法。改进的算法在标准粒子群算法模型的基础上，融入了高斯变异以及差分进化算法的交叉变异机制，并将本文算法与典型的三种差分进化粒子群算法（DEPSO）在不同目标函数上进行仿真对比。

3.1 算法思想

算法保留了粒子群模型的速度向量，采用常用的一种差分变异策略，增加粒子的多样性，保证全局搜索能力，但由于目标向量是速度向量，故在此基础上将基向量改为，并加入基于群体最优的差分向量，加速种群收敛速度，加强了对群体最优附近区域的挖掘能力[6]。文献[11]中采用了对于最优向量中某一维分量变异的策略得到了很好的效果，在本文算法的高斯变异操作中，只对速度向量的某一维分量进行变异。另外为了进一步加强算法在群体最优附近的挖掘能力，引入高斯变异在最优位置附近进行搜索。有研究指出，全局最优解易出现在粒子群的群体最优位置与个体最优之间[7]，受此启发，本文算法中取群体历史最优位置和历史次优位置之间的区域进行高斯变异。这么选择首先使高斯变异的范围根据搜索进程进行变化，搜索前期范围较大，搜索后期范围会缩小。其次是因为在算法收敛后期问题的解多在群体最优位置附近，当粒子位置（由于算法的选择操作，粒子个体最优即是粒子当前位置）未越过最优解时，算法会使粒子向最优解移动并记录上次最优位置，当粒子由于速度惯性越过最优解时，问题的解便在历史最优位置和历史次优位置之间，所以说这个范围是最具价值的搜索空间。实验证明这种方式对于单峰及多峰函数起到了局部挖掘，促进收敛的作用。

根据上述原理，本文算法步骤如下：

（1）初始化。初始化种群个数，迭代次数，以及所有粒子的位置和速度。

（2）计算每个粒子的适应度值，初始化种群个体历史最优和群体最优。

（3）判断是否达到结束条件，如是则输出当前全局最优值，否则执行下面步骤。

（4）对粒子速度向量中随机选择的一维，按照下面公式进行变异。更新粒子位置后采用差分进化算法的选择机制，与之前粒子位置的适应度值进行比较，若当前粒子比之前粒子的适应度值更优，则用当前粒子进行替换，否则保留前一代粒子到下一代。

（5）记录粒子群的历史最优及历史次优，采用下式进行高斯变异，在历史最优与历史次优之间进行挖掘，寻找更优的粒子对当前最优粒子进行替换，并更新次优粒子位置。

（6）返回步骤（3）。

3.2 数值仿真

将本文提出的算法与标准粒子群算法（PSO）、差分进化算法（DE）以及三种典型的差分进化与粒子群的结合算法[8]（本文将其称为：I辅助式[9]、II集成式[10]和III协作式[11]）进行对比，选用Ackley多峰函数、Griewank函数、Rastrigin函数、Rosenbrock函数四种测试函数作为算法的目标函数，仿真结果如图3及表1所示。

由图3可知，本文改进算法在Rastrigin多峰函数优化上的优势显著，PSO算法和DE算法以及类型II均陷入了局部最优，类型I和类型III的改进算法依然继续搜索趋势，但与本文所提算法相比速度极慢。在其他函数如Rosenbrock函数仿真结果上，相比于其他算法，本文改进算法达到更高精度，表现出在此单峰问题求解中的优势。

4 对加热炉-对流换热系统辨识

4.1 加热炉换热器控制系统的组成

将本文的辨识方法应用到加热炉换热器双入双出耦合对象，控制系统的方框图如图4所示。其输出为内胆温度T1和换热器冷却水出口温度T2，輸入为控制器1和控制器2的输出信号即加热器与变频器的开度信号U1和U2。故设计神经网络辨识模型的输出为T1和T2，输入为U1和U2。

训练样本以5秒的采样间隔取控制回路闭合时加入换热器冷却水出口温度设定值后500秒内的100组控制器的输出以及温度数据，所有试验数据做归一化处理，训练次数为300次。

4.2 仿真对比及结果分析

将本文方法与采用BP学习的OIF-Elman网络及采用上述类型III优化算法的OIF-Elman网络进行对比，如图5所示。经过训练，三种网络模型均收敛到了一定的精度，本文提出的网络模型相比于BP算法OIF-Elman网络及类型III-OIFElman网络以较少的训练次数收敛到了较高精度。表2为三种模型的辨识误差，同时也加入了标准Elman神经网络的辨识误差作为对比，可以看出采用本文算法的OIF-Elman网络的辨识精度更高。

图6为三种网络模型对训练样本输出信号的拟合曲线，更加直观地展现出网络模型的辨识效果，由图可见，同样是采用本文算法的OIF-Elman网络模型相比其他两种模型对于样本的拟合效果更好。

5 结束语

加热炉换热器对象是一个多入多出的动态过程，采用OIFElman这种递归型神经网络对加热炉换热器对象闭环调节过程的实验数据进行了辨识，得到具有一定精度的神经网络模型。采用BP算法，网络的隐层节点较多，收敛速度慢，且精度不高。采用粒子群等智能算法优化神经网络权值、阈值、关联系数、关联层初始值，较之BP算法，智能优化算法表现出了较快的收敛速度与精度，省却了人为给定关联系数及关联层初值这一步骤，同时表现出了较强的搜索能力，简化神经网络的复杂性，得出了在同样规模的神经网络结构下BP算法无法搜索到的解。本文提出的混合算法较之多种改进的差分进化粒子群算法在仿真结果上表现出较好的搜索能力，并应用到神经网络对象辨识中，针对加热炉换热器对象得到了一种结构简单，精度更高的神经网络模型。

参考文献：

[1]茹菲，李铁鹰.人工神经网络系统辨识综述[J].软件导刊， 2011，10（03）：134-135.

[2]章国升.基于递归神经网络的非线性系统辨识研究[D].兰州： 兰州大学，2010.

[3]时小虎，梁艳春，徐旭.改进的Elman模型与递归反传控制神经网络[J].软件学报，2003，14（06）：82-91.

[4]王琛.超超临界机组非线性动态模型的研究[D].北京：华北电力大学（北京），2010.

[5]姚柳.超超临界机组的建模与仿真[D].北京：华北电力大学（北京），2011.

[6]宋锦，师玉娇，高浩等.基于新型变异策略的差分进化算法[J].计算机工程与设计，2016，37（05）：1285-1290.

[7]Gao H，Xu W. Particle Swarm Algorithm with Hybrid Mutation Strategy[J]. Applied Soft Computing， 2011， 11（8）： 5129-5142.

[8]辛斌，陈杰.粒子群优化与差分进化混合算法的综述与分类[J]. 系统科学与数学，2011，31（9）：1130-1150.

[9]Zhang W，Xie X.Depso：Hybrid Particle Swarm with Differential Evolution Operator[C]//Proceedings of the Ieee International Conference on Systems，man，and Cybernetics， [S.l.]：[s.n.]，2004：3816-3821.

[10]Jun S，Jian L.A Hybrid of Differential Evolution and Particle Swarm Optimization for Global Optimization[C]//Proceedings of the 3rd International Symposium on Intelligent Information Technology Application，[S.l.]：[s.n.]， 2009：138-141.

[11]Niu B，Li L.A Novel Pso-de-based Hybrid Algorithm for Global Optimization[C]//Proceedings of the 4th International Conference on Intelligent Computing，[S.l.]：Springer Berlin Heidelberg，2008：156-163.

作者简介：黄伟（1966-），女，副教授，研究方向：智能控制、系统辨识、电气设备状态检测与故障诊断。

*为通讯作者