变压器绕组温升试验不确定度评定

2017-03-16乐洋铄

山东工业技术 2017年3期

关键词：不确定度变压器

乐洋铄

摘要：结合绕组温升试验和不确定度评定和标示公式，本文就电阻法测变压器绕组温升项目涉及到的部分影响结果的因素进行了归纳和不确定度的计算。

关键词：绕组温升；不确定度；变压器

DOI：10.16640/j.cnki.37-1222/t.2017.03.039

1 测试概况

电器安全测试中的温升试验是比较常见的，变压器因为其绕组特性，工作时温度较高，影响变压器安全性。测量绕组温升一般有热电偶法和电阻法，预埋热电偶比较复杂而且某个点的温度也不能代表绕组整体水平，所以标准规定除非绕组是不均匀的，或是难于进行必要的连接，才使用热电偶法，一般采取电阻法测绕组直流电阻再换算成温升。

绕组法测温升的原理是：铜、铝等金属，因其电阻随温度的改变会有特定的规律的变化。实验之前需对样品和环境进行预处理，使之均达到热平衡状态。根据电阻法公式，需要测得试验开始时的电阻、室温，试验结束时的电阻室温，并确定k值。由于无法在断电瞬间测得试验结束时电阻，所以在断开开关后需要通过短时间间隔多次测量的电阻值，采用倒推法拟合曲线或绘图等方式，确定开关断开瞬间的热态电阻电阻值。

由于电阻法测绕组温升试验能同时考核实验室在样品处理、测试方法、环境控制能力等几个方面的能力，所以经常运用在跨实验室的能力验证比对中。而又由于不同实验室在试验技术、样品制备、实施过程中的不同，甚至一些偶然因素也会影响试验结果，所以部分能力验证组织方要求在提供试验结果的同时还需要提供不确定度影响因素及不确定度的要求。

2 预处理

对样品和环境进行标准要求的预处理是测量绕组温升得到准确结果的先决条件。根据选择的标准GB4706.1-2005实施和能力验证组织方的有求，在把实验室环境温度控制在23℃±1℃范围内，设置好测试角，连接好负载，测试用导线和监测环境和绕组温度的热电偶，在试验开始之前变压器样品在符合要求的环境下摆放至少24h，确保热平衡。

3 试验流程

（1）变压器样品热平衡后，测初始绕组阻值R1及对应环境温度t1。

（2）仔细阅读作业指导书，按要求连接电源，负载，调节负载阻值，使用功率计监测变压器初次极两端电压电流符合作业指导书要求。

（3）使用热电偶监测环境温度和变压器绕组温度，确保环境温度在23℃±1℃范围内，绕组工作至符合作业指导书要求且温度达到最高且稳定，即变压器在1h时之间温度变化不超过1℃，就认为是热平衡状态。

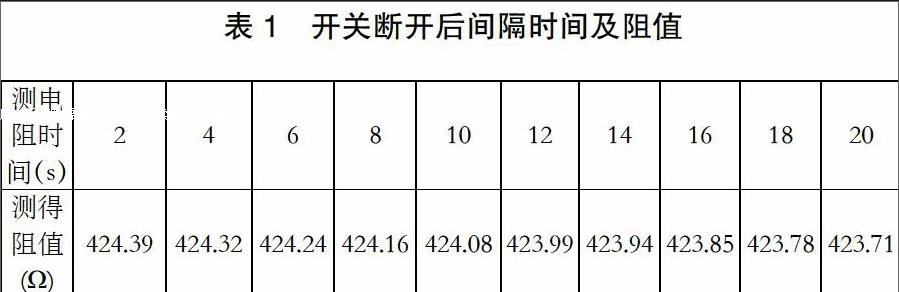
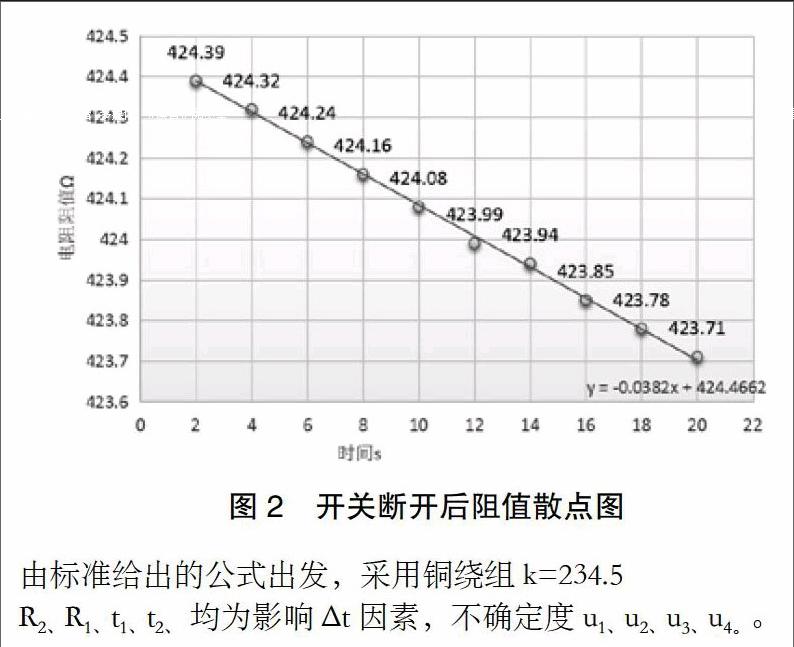
（4）断电后，使用直流电阻测试仪记录短时间内间隔的多个电阻阻值，并画热态电阻阻值散点图并通过曲线拟合的方式确定开关断开瞬关阻值R2。

由标准给出的公式出发，采用铜绕组k=234.5

R2、R1、t1、t2、均为影响Δt因素，不确定度u1、u2、u3、u4。。

4 不确定度评定

4.1 开关断开瞬间热态电阻引入不确定度分量u1

断电后，隔一段时间测得的一系类阻值y与取值得时间t可作散点图，并根据最小二乘法进行线性回归，此方法引入的不确定度采用A类评定。

设方程为

设xi=（ti-2），则方程体现为：