物流服务供应商选择的组合赋权—灰色综合决策

陈可嘉 李烜楠

(福州大学经济与管理学院， 福建省金融科技创新重点实验室, 福建福州 350116)

物流服务供应商选择的组合赋权—灰色综合决策

陈可嘉 李烜楠

(福州大学经济与管理学院， 福建省金融科技创新重点实验室, 福建福州 350116)

为了提高港口企业选择物流服务供应商的科学性，提出一种用于解决供应商选择问题的组合赋权—灰色综合决策方法。该方法首先将网络分析法和熵值法相结合以确定评价指标的组合权重，接着引入改进中心点三角白化权函数对备选方案进行聚类并判断其所属的灰类，再利用综合加权决策向量求得灰色综合决策系数向量，然后通过计算灰色综合聚类决策系数对备选方案进行综合决策排序。最后以某家港口企业对物流服务供应商的选择进行实证研究以验证该方法的有效性。

物流服务； 供应商选择； 组合赋权； 灰色综合决策

在市场环境下，企业对物流服务供应商的合理选择是其所需要面临的重要问题之一。由于评价过程的不确定性，使得该问题呈现出灰色性，并导致其成为一个复杂的多属性决策问题。[1]当前我国各地港口企业的物流服务供应商基本以中小型企业为主，这些企业的整体实力和运作规范程度都不够高，其提供的物流服务的品质有时也很难让港口企业满意。因此，对港口企业物流服务供应商的选择策略进行研究，对于港口企业提高运作效率和运营水平都具有一定的现实意义。

针对该问题，已有许多学者做了相关研究。Jharkharia和Shankar在评价指标体系中引入了物流服务供应商的兼容性，最后通过网络分析方法(ANP)进行供应商选择。[2]Xu和Zhang在供应商选择问题当中引入了灰色聚类方法，建立了灰色聚类的决策模型，来进行供应商的评价工作。[3]邹平和袁亦男认为可拓学中可拓集合和物元概念的可拓层次分析法能很好地弥补AHP这个缺陷，并且在评价过程中考虑了灰色关联法，构建了一种EAHP和GRAP相结合的供应商评价模型。[4]王旭等构建了一种双层的规划模型，分别以物流成本和顾客满意度为优化目标，并用熵值法求出各指标的权重，最后采用云自适应遗传算法求解该模型。[5]陈虎以物流成本和服务质量为出发点构建了双层规划模型，在此基础对QFD模型进行了重新构建，并运用AHP对物流服务供应商进行综合评价。[6]王燕和谢蕊蕊首先对供应商的物流实力、成本价格、服务质量、合作风险四个部分采用ANP方法求得相应权重，再运用VIKOR进行最后的排序。[7]Chen等将灰关联与topsis方法相结合，提出了一种组合赋权GI-TOPSIS方法用于解决物流服务供应商选择问题。[8]刘荣娟和赵道致使用熵权法，对低碳经济模式下的供应商选择问题进行了考察。[9]Zhou提出了灰色聚类和熵权法相结合的多目标决策模型，用于最优供应商的选择。[10]袁宇等通过转换和规范化处理多种混合数据，将信任度函数和熵权法进行结合来对决策者和决策准则进行客观赋权，由此构建了基于混合信息的VIKOR方法来对供应商进行评价。[11]伍星华等根据评价指标的灰色特征和指标间的关联性，将灰色系统理论和网络层次分析法相结合，运用于物流服务供应商的评价和选择。[12]Rajesh和Ravi使用灰色关联法对供应商进行选择，并通过权重的变化，来对选择结果变化的敏感性进行研究。[13]Pitchipoo等采用熵值法和主成分分析法相结合的方式求解组合权重，接着采用灰色关联法进行供应商的选择。[14]2014年，刘思峰等改进了原有的中心点三角白化权函数，针对灰类1取下限测度白化权函数，而对于灰类s则取上限测度白化权函数，经过改进的中心点三角白化权函数有效地解决了评价指标在进行构建时的延展困扰。[15]

综上所述，现有的物流服务供应商选择研究存在一定的不足之处，如指标体系不能很好地反映指标间相互依赖的作用关系；指标权重的求解方式过多地依赖专家判断等主观因素，对客观因素的重视程度不够高；对问题的灰色性处理的方式不够恰当等等。此外，在现有的文献中，关于灰色综合决策方法在港口企业的物流服务供应商选择问题当中的应用研究较少。因此，本文在供应商的评价指标权重确定上不仅考虑到专家判断等主观因素，还考虑了评价指标数据的客观信息以及问题的灰色性，提出了组合赋权—灰色综合决策方法来帮助企业解决物流服务供应商选择的问题，并且以一家港口企业作为实证研究的对象，来验证该决策方法的有效性。

一、港口企业物流服务供应商的评价指标体系

(一)评价指标体系的构建

本文基于已有研究成果，构建了港口企业选择物流服务供应商的评价指标体系，如表1所示。

(二)评价指标体系的信度效度结果分析

根据以上构建的评价指标体系，采用问卷调查的方式，来对各个评价指标的重要程度进行评分。

1. 信度分析

通过信度分析得出该问卷的整体信度系数为0.738。说明该问卷的内部一致性和信度较好。

2. 效度分析

根据效度分析的结果，将二十组二级评价指标归纳到五组一级评价指标之中，如表1所示。

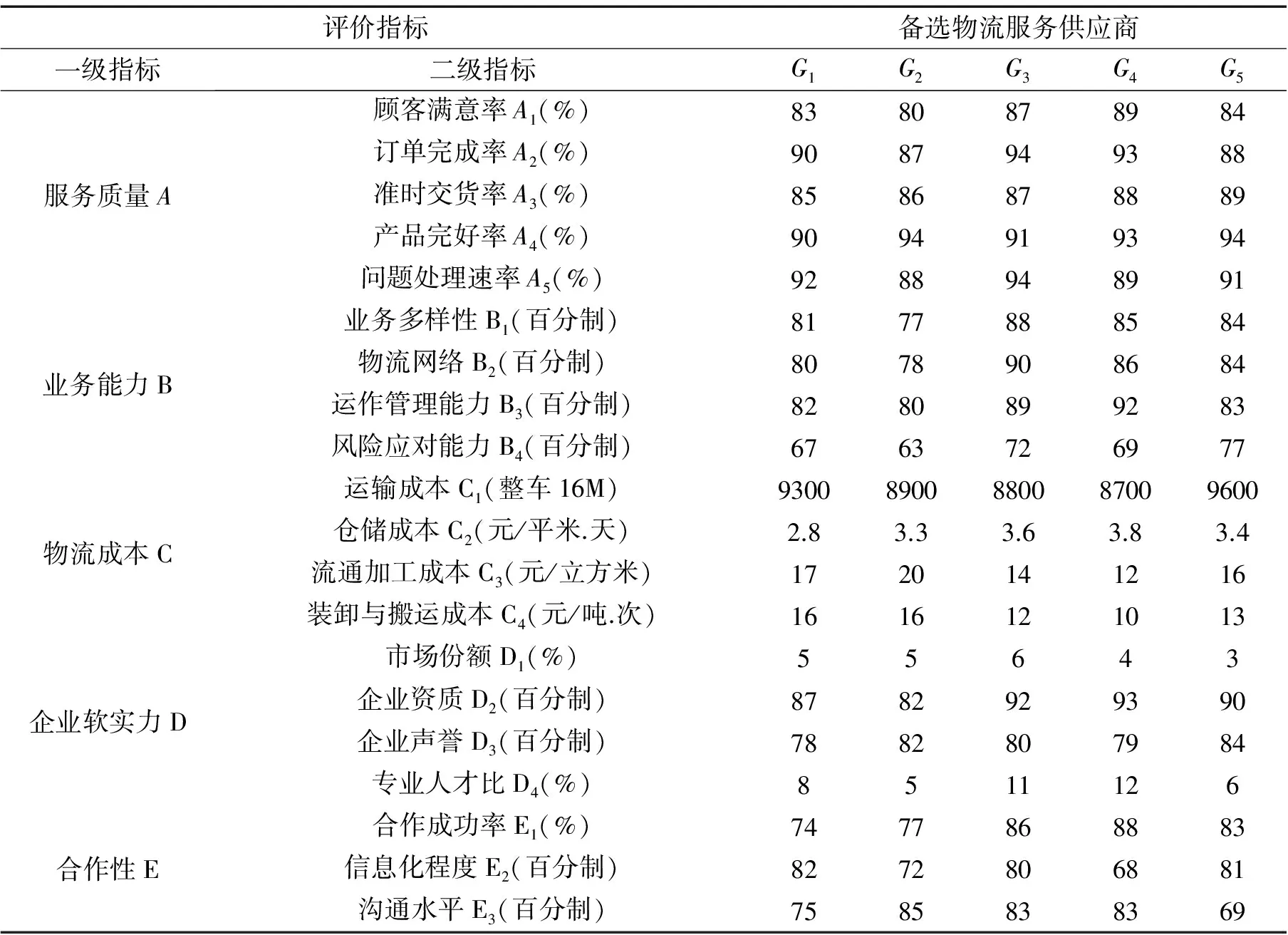
表1 物流服务供应商评价指标体系及其评价数据

二、组合赋权—灰色综合决策方法

对于某一物流服务，假设市场上总共有m个备选方案。企业用来对备选方案进行评价的评价指标总共有n个。备选方案i(i=1,2,…,m)关于评价指标j(j=1,2,…,n)的评价数据为xij(i=1,2,…,m;j=1,2,…,n)。本文总共划分了s个灰类，灰类k(k=1,2,…,s)。wj=(w1,w2,…,wn)代表各评价指标的权重。本文所提出的组合赋权—灰色综合决策方法的决策步骤如下所示。

(一)组合赋权

1. 基于ANP的主观权重确定

ANP的网络结构主要由两个部分组成：控制层与网络层。元素之间可以分为外部影响、内部影响和相互影响三种关系。最后，对极限矩阵进行求解，以得出各个评价指标的主观权重sj。

2. 基于熵值法的客观权重确定

由于各个评价指标的量纲存在一定的差异性，因此，在使用熵值法求解客观权重之前，有必要先对评价数据xij进行相应的规范化处理。当评价指标为正向型指标时或逆向型指标时，分别采用规范化公式(1)、(2)将评价数据xij转换成无量纲的评价数据rij。

(1)

(2)

经过规范化处理后，再采用熵值法求解出各个评价指标的客观权重oj。

3. 组合权重的计算

通过公式3来对主客观权重进行组合赋权。计算公式如下所示：

(j=1,2,…,n) (3)

(二)灰色综合决策方法

1. 评价指标灰类的转折点或中心点的确定

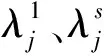
2. 相应的灰类白化权函数的构建

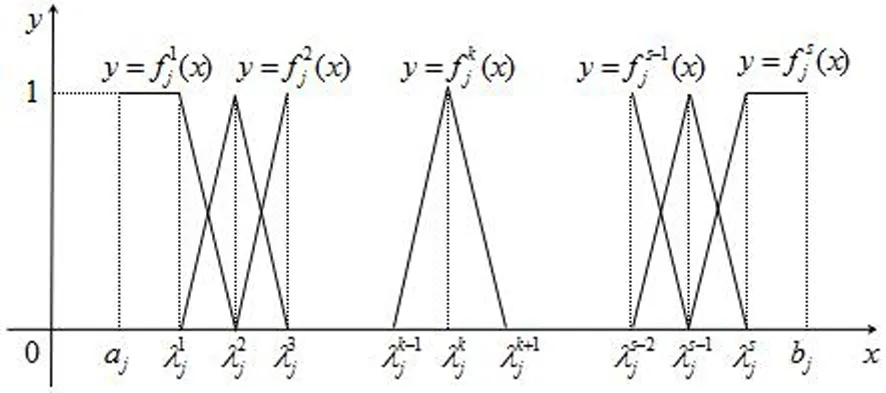
图1 改进中心点三角白化权函数示意图

3. 灰色聚类系数的计算

采用公式(4)可以求出备选方案i(i=1,2,…,m)关于灰类k(k=1,2,…,s)的灰色聚类系数为：

(4)

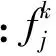
4. 备选方案所属灰类的判断

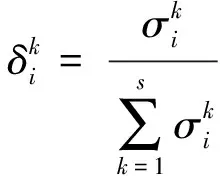
5. 综合加权决策向量的计算

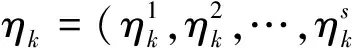
(5)

6. 灰色综合决策系数向量的计算

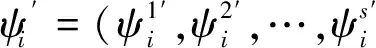
(6)

7. 灰色综合聚类决策系数的计算

令灰色综合聚类决策系数的权向量为γ=(1,2,…,s-1,s)T，则可以通过公式(7)得出备选方案i的灰色综合聚类决策系数：

(7)

与此同时，可以求得该决策系数矩阵如下所示：

为s，最小值为1。所以，1≤πi≤s。

8. 综合决策排序

通过对比灰色综合聚类决策系数的大小来对同一个k灰类内的备选方案进行综合决策排序。

三、实证研究

某港口企业主要生产各种混凝土垫块以及水运工程建设中所使用的小型混凝土预制构件等材料，其所生产的产品被广泛应用于水运工程、楼房、道路等建筑。由于该港口企业战略目标和资金分配的限制，企业决定选择物流服务供应商帮助其处理物流业务。现采用组合赋权—灰色综合决策方法来对备选供应商进行选择和评价，其中，各个备选供应商的评价数据如表1所示。

(一)港口企业物流服务供应商选择的评价指标组合赋权

采用前文的组合赋权方法，求得物流服务供应商评价指标的组合权重，结果如表2所示。

(二)港口企业物流服务供应商选择的灰色综合决策

1. 评价指标灰类的转折点或中心点的确定

依据评价要求，将该企业选择物流服务供应商的各个评价指标划分为差、中、良、优4个灰类，如表2所示。

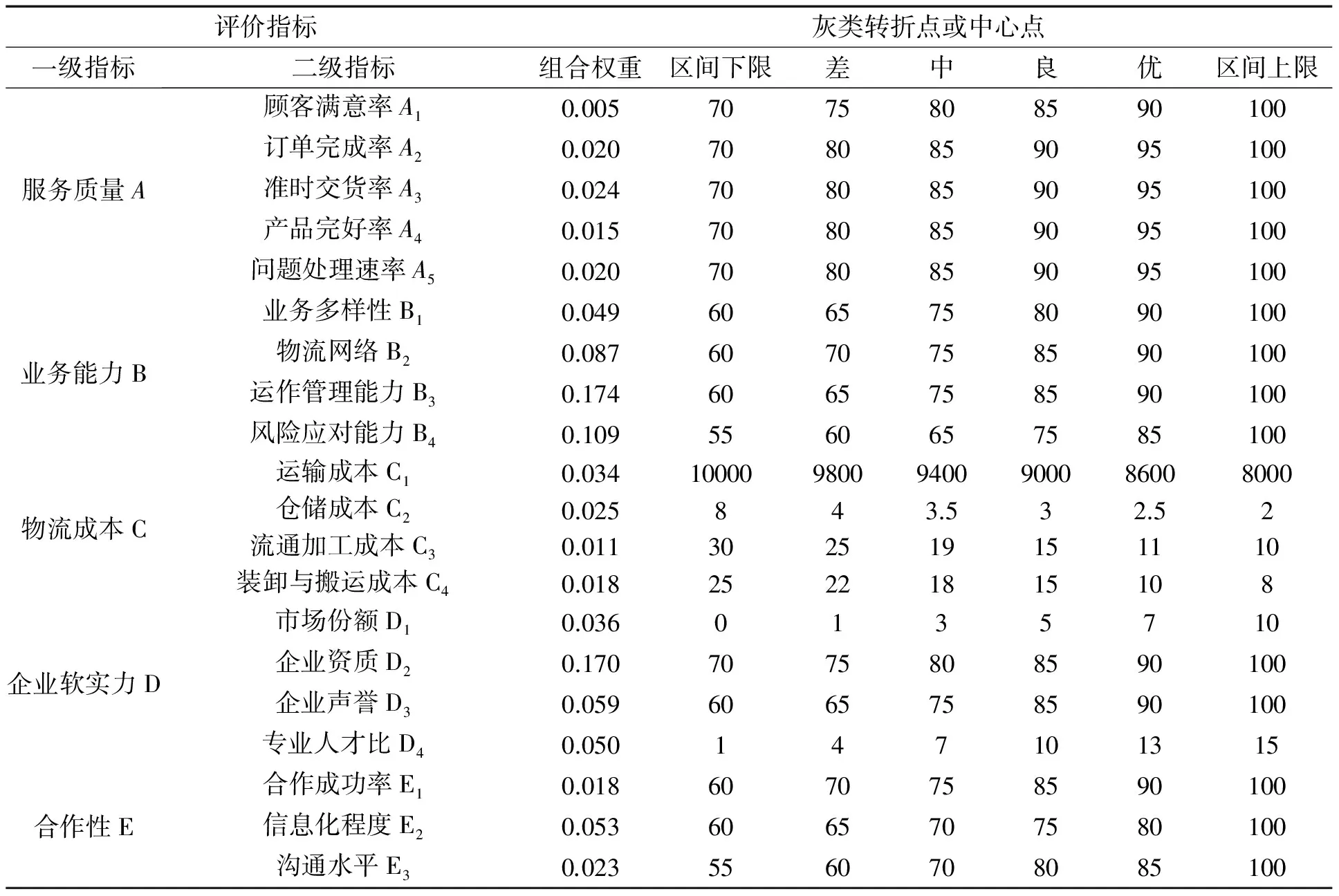
表2 物流服务供应商评价指标组合权重及其灰类划分

2. 相应的灰类白化权函数的构建

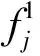
3. 灰色聚类系数的计算

对各个备选供应商的灰色聚类系数进行计算，并将结果进行汇总，如表3所示。

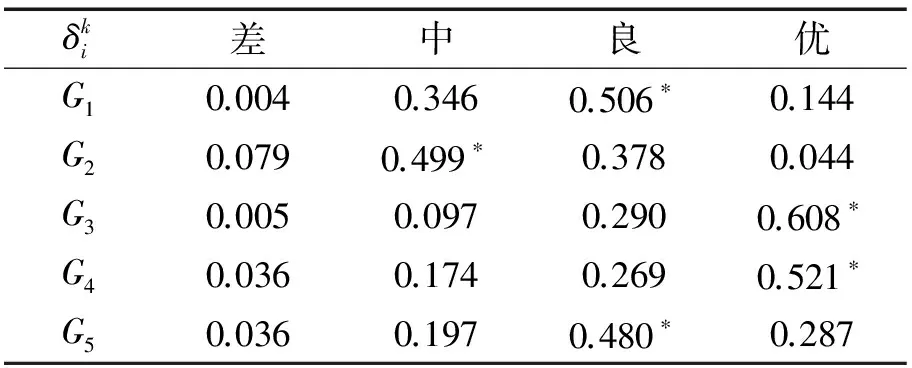
表3 供应商灰色聚类系数计算结果汇总

4. 供应商所属灰类的判断

通过观察各个备选供应商灰色聚类系数的最大值，可以判断出该供应商所属的灰类，结果如表4所示。

表4 供应商所属灰类判定

5. 综合加权决策向量的计算

因文中共涉及4种灰类，可以计算得出灰类k的综合加权决策向量为：

6. 灰色综合决策系数向量的计算

计算各个备选供应商关于灰类k的初始灰色综合决策系数，并对其进行归一化处理后可以得到灰色综合决策系数矩阵如下：

7. 灰色综合聚类决策系数的计算

通过计算求得各个备选供应商的灰色综合聚类决策系数πi，如表5所示。

表5 供应商灰色综合聚类决策系数

8. 综合决策排序

根据表4和表5的结果可以得知：G2属于中灰类；G1和G5属于良灰类，由于2.673>2.593，所以可知G5优于G1；G3和G4属于优灰类，由于2.840>2.760，所以可知G3优于G4。最后的备选供应商排序为：G3>G4>G5>G1>G2。结果表明，供应商G3具有最大的灰色综合聚类决策系数，供应商G4次之，而供应商G2则相对较差，因此，该港口企业应选择供应商G3作为其合作伙伴，帮助其处理物流业务。

而在实际情况中，供应商G3是集物流方案策划、货运代理、普通货物运输、仓储配送、货物包装分拣和汽车维修检测功能为一体的第三方物流企业。其经营场所70多万平方米，自有运输车辆1300多部，员工6700多人，并于2011年获得国家物流企业的最高资质等级5A级。由于该供应商在订单完成率、问题处理速率、业务多样性、物流网络、市场份额以及企业资质上，相较于其他供应商，表现得较为突出，对于委托方的需求满足程度较高。因此，该家港口企业选择物流服务供应商G3，与其实施物流战略联盟。

通过上述结论可知，组合赋权—灰色综合决策方法所得结果与该港口企业的供应商选择实际情况相符，证明了该方法可以对港口企业的各物流服务供应商进行有效的区分与排序。

(三)可靠性分析

可靠性分析是将文中构建的评价方法与其它方法得到的评价结果进行比较，以验证评价结果是否具有较好的一致性。[16]为了验证所建立的组合赋权—灰色综合决策方法的可靠性，本文还用网络层次分析法和灰色聚类法对该问题进行物流服务供应商的选择，其对比结果如表6所示。

表6 排序结果对比

根据对比结果，本文所提出的方法与另外两种方法的评价结果高度吻合，使得该评价方法的可靠性得到了验证。

四、结论

1. 随着行业专业化分工的逐步细化与深入，许多企业选择把公司的非核心业务交由合作供应商来完成，这样可以让企业把主要精力放在关键的业务上，使其能更好集中优势资源，增强核心竞争能力，扩大经营规模以及开辟新的市场。因此，对物流服务供应商的正确选择，是企业在供应链管理中必须考虑的重要问题。对于一家港口企业来说，正确地选择出合适的物流服务供应商，能够让物流业务成为企业的竞争优势，促使企业快速发展；否则，会影响企业的经营状况，导致企业的资金、时间和人力的浪费。

2. 关于物流服务供应商的选择问题，由于在评价过程中呈现出的灰色性，使得该类问题成为了一种复杂的多属性决策问题。为了使评价过程更加科学和合理，本文首先建立了港口企业物流服务供应商选择的指标体系，通过信度和效度分析，对所建立的评价指标体系的合理性进行检验，并且将这些指标归纳为服务质量、业务能力、物流成本、企业软实力和合作性等五个一级指标。接着，提出了一种用于解决港口企业供应商选择问题的组合赋权—灰色综合决策方法。使用网络分析法(ANP)与熵值法相结合的方式来对评价指标的主客观权重进行组合赋权，以求得各指标的组合权重，接着引入改进中心点三角白化权函数对备选方案进行灰色聚类和灰类判断，通过计算综合加权决策向量来求得灰色综合决策系数向量，然后求解灰色综合聚类决策系数对备选方案进行决策排序。

3. 以一家港口企业的物流服务供应商选择案例，作为实证研究的对象，验证了该评价指标体系与评价方法的有效性和稳定性。

注释：

[1] Thakur V. , Anbanandam R. , “Supplier selection using grey theory: a case study from Indian banking industry”,JournalofEnterpriseInformationManagement, vol.28, no.6 (2015), pp. 769-787.

[2] Jharkharia S. , Shankar R. , “Selection of logistics service provider: an analytic network process (ANP) approach”,Omega, vol.35, no.3 (2007), pp. 274-289.

[3] Xu P. , Zhang Q. S. , “Decision - making model of grey clusterng for supplier selection”,JournalofHarbinInstituteofTechnology, vol.39, no.12 (2007), pp. 2006- 2008.

[4] 邹 平、袁亦男:《基于EAHP和GRAP的供应商选择》,《系统工程理论与实践》2009年第3期。

[5] 王 旭、石 琳、葛显龙:《物流服务供应商选择的双层规划模型及云遗传算法》,《计算机应用研究》2011年第8期。

[6] 陈 虎:《基于QFD和双层规划的物流服务供应商选择研究》,《计算机工程与应用》2012年第27期。

[7] 王 燕、谢蕊蕊:《物流外包合作伙伴选择的两阶段混合决策方法——基于DEMATEL-ANP-VIKOR混合决策模型》,《中国流通经济》2012年第8期。

[8] Chen K. J. , Yu X. K. , Yang L. X. , “GI-TOPSIS based on combinational weight determination and its application to selection of reverse logistics service providers”,TheJournalofGreySystem, vol.25, no.3 (2013), pp. 16-33.

[9] 刘荣娟、赵道致:《低碳经济发展模式下供应商选择问题研究》,《北京交通大学学报》(社会科学版)2014年第1期。

[10] Zhou Y. W. , “The research on supplier selection model of the third party logistics based on grey clustering”,InternationalJournalofModelingandOptimization, vol.4, no.6 (2014), pp. 489-492.

[11] 袁 宇、关 涛、闫相斌等:《基于混合VIKOR方法的供应商选择决策模型》,《控制与决策》2014年第3期。

[12] 伍星华、姚 珣、李思寰:《低碳物流服务供应商选择的GST-ANP模型研究》,《科技管理研究》2015年第20期。

[13] Rajesh R. , Ravi V. , “Supplier selection in resilient supply chains: a grey relational analysis approach”,JournalofCleanerProduction, no.86 (2015), pp. 343-359.

[14] Pitchipoo P. , Venkumar P. , Rajakarunakaran S. , “Grey decision model for supplier evaluation and selection in process industry: a comparative perspective”,TheInternationalJournalofAdvancedManufacturingTechnology, no.76 (2015), pp. 2059-2069.

[15] 刘思峰、方志耕、杨英杰:《两阶段灰色综合测度决策模型与三角白化权函数的改进》,《控制与决策》2014年第7期。

[16] 马 毅、王希良、朱秀嫚:《基于联系数的定量与定性分析方法在调车作业安全评价中的应用》,《系统工程理论实践》2013年第6期。

[责任编辑：黄艳林]

2016-09-14

国家自然科学基金项目(71601050); 教育部新世纪优秀人才支持计划(NCET-11-0903)。

陈可嘉， 男， 福建福州人， 福州大学经济与管理学院教授、 博士生导师， 博士； 李烜楠， 男， 福建福州人， 福州大学经济与管理学院硕士研究生。

F274

A

1002-3321(2017)01-0028-06