基于改进模糊神经网络算法的炮兵火力运用方案评估*

刘 铜,李小全,王永良,王 键

(1.南京炮兵学院,江苏 南京 211132;2.解放军65565部队,辽宁 丹东 118105)

基于改进模糊神经网络算法的炮兵火力运用方案评估*

刘 铜1,李小全1,王永良1,王 键2

(1.南京炮兵学院,江苏 南京 211132;2.解放军65565部队,辽宁 丹东 118105)

针对炮兵火力运用方案评估中的主观性和不确定性等问题,将模糊理论融入到BP神经网络对其进行评估,并通过多种群自适应遗传算法对神经网络进行优化以提高评估的效率。构建了炮兵火力运用方案评估指标体系、评估流程和评估模型。最后,结合实例进行了仿真验证分析,得出了较为可靠的结论,为炮兵火力运用方案评估提供了有效方法。

炮兵火力运用方案;评估;神经网络;模糊理论

联合作战下,炮兵作为对地火力突击的主体力量,火力运用的正确与否直接影响到指挥员的战斗决心。面对瞬息万变的复杂战场情况,要求炮兵指挥员必须快速准确地进行炮兵火力运用决策。而炮兵火力运用方案即预先制定的炮兵火力计划,是炮兵火力运用的书面形式,它的优劣将直接影响炮兵火力打击效果,甚至影响整个作战全局。因此,炮兵火力运用方案评估在炮兵作战指挥决策中非常关键。

目前,针对炮兵火力运用方案评估的研究较多,文献[1]运用非结构模糊决策与AHP法相结合的三标度层次分析法对炮兵火力计划进行评估优选,考虑到了评估中半结构化的问题,但是没有解决主观因素的影响;文献[2]建立模糊物元理想解模型优选炮兵火力计划方案,采用层次分析法求取指标权重,借助欧氏范数计算相似贴近度,得出较高可信度的评估结果,但仍然会受到主观因素的影响。文献[3-5]针对炮兵火力计划方案评估中存在的不确定性,提出使用灰色局势理论对其进行评估,但是最终没有能够避免主观因素的影响。文献[6]采用神经网络的算法对炮兵火力运用方案进行评估,避免了主观因素的影响,但是没有考虑到算法的评估效率和炮兵火力运用方案的不确定性问题。针对这些问题,本文提出采用改进模糊BP神经网络算法对炮兵火力运用方案进行评估,以提高评估的效率,为研究炮兵火力运用方案评估提供指导和借鉴。

1 炮兵火力运用方案评估

1.1 炮兵火力运用方案评估流程

炮兵火力运用方案的评估是炮兵指挥员进行作战决策的关键环节。评估主要分为三个阶段：第一阶段是拟制方案前的准备工作；第二阶段是拟制方案；第三阶段是评估优选阶段。准备阶段主要完成的工作包括受领任务、根据任务收集侦察目标情报、分析判断情况,完成拟制方案前的准备工作。评估优选阶段主要工作包括构建评估模型和进行评估优选,其中构建评估模型包括建立评估指标体系、选择评估算法和评估实施三个过程。具体流程,如图1所示。

图1 炮兵远程火力毁伤评估流程图

1.2 炮兵火力运用方案评估指标体系

科学的评估指标体系是进行评估的前提。结合炮兵火力运用的相关作战原则和要求,确定的评估指标包括合理性、适应性、完整性、一致性、效益性和经济性几个方面。合理性包括打击目标的选择、分配和射击任务确定的合理性;适应性是指方案能够适应不断变化的战场的程度;完整性是指方案内容的完整性和要素齐全程度;一致性主要是指与上级任务和本级任务一致的程度;效益性是指计划完成的任务量满足作战任务的程度;经济性主要是指在火力打击过程中消耗弹药的多少,具体指标体系如图2所示。

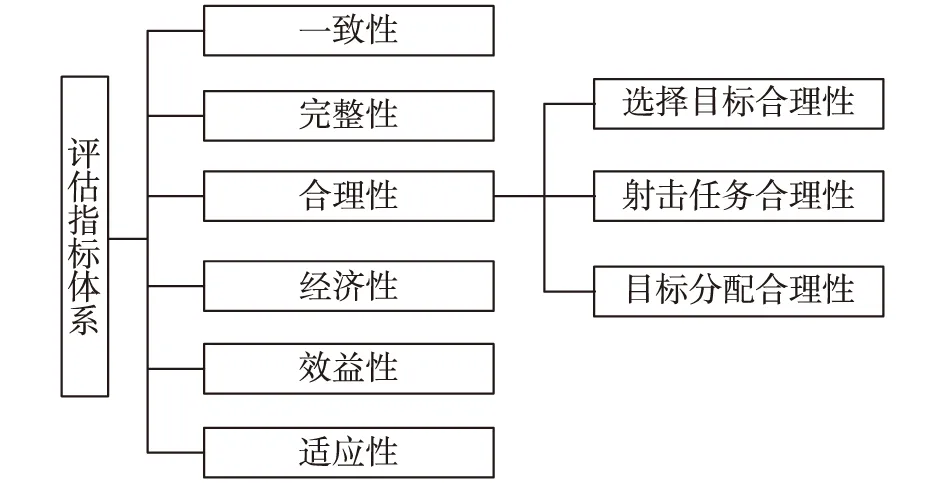
图2 评估指标体系

2 关键算法及理论

2.1 模糊BP神经网络算法

图3 模糊BP神经网络结构图

模糊BP神经网络第一层为输入层,同普通的神经网络相同,它的输入值与输出值不变,如下式所示。

第三层为模糊推理层，在模糊神经网络中往往是通过一系列if-then的模糊推理规则形式来描述输入同输出之间的映射关系。设共有M条模糊规则,则其中第i条规则为:

Rulei:ifχ1isA1Iandχ2isA2i…andχmisAmi,

theny=fi(χ1,χ2,χ3…χm)

其中,χi,i=1,2,3…M为模糊推理的输入变量,y为模糊推理的输出变量,Aki,k=1,2,3…M为输入变量在论域中的语言标志模糊集合的子集,Aki的隶属函数是可选的。fi(χ1,χ2,χ3…χm)为输出结果。

第三层的节点数为N个,可以根据具体的网络结构进行调整,这一层的节点输出经过模糊运算后得出,可以选择模糊交集或者选择连乘算子作为模糊推理规则来进行计算,其输入输出式为:

i=1,2…M,jk=1,2…mk,k=1,2…M

第四层为输出层,即去模糊化层,该层只有一个节点,该节点计算所有传来的输入变量之后并作为最终的输出,如下式所示。

2.2 自适应遗传算法

在自适应遗传算法中,采用多子群的结构可以通过将动态选择过程中的选择与保存概率、交叉和变异概率进行适当的改进,使它们的值随着个体适应度的变化而相应发生变化,而不是固定不变的,这样可使个体更好地向极值方向收敛。

在进行遗传过程中的优秀个体选择时,可以通过带约束参数的动态选择概率与最优个体保存策略的混合选择机制来实现优秀进化个体的选择。通常,遗传算法的选择策略是与适应度值成比例的,如下式所示。

其中,pj表示个体在下一代的遗传进化中被选中的概率,fα(χj)表示个体χj在种群中的适应度值,N表示种群的大小，即种群中个体的数量,0<α<∞。当α=1时,选择算子被称为等比例算子,轮盘选择算子就属于这一类,可以证明,当α的值越大时,参与遗传进化的适应度函数值越大的个体被选择的几率越大,当α的值越小时,参与遗传进化的各个个体被选中概率会非常接近,从而导致个体选择的随机性变大。同时,α的值很大时,仅会在参与遗传进化的适应度函数比较大的个体中选择,选择的空间会比较小,可能丧失掉收敛到最优解的机会,而当α的值很小时,整个选择的过程会在种群的所有个体中进行,会导致进化的搜索效率非常低,因此α的选取是非常重要的。在改进的算法中,采用α=e-t,其中t表示进化的代数,以此来进行个体的选择,然后再进行个体的交叉与变异操作。

在遗传中的交叉和变异概率改进时,针对每一次的进化计算出每一个种群适应度值的标准差,根据其标准差的分布情况动态地调整交叉变异的概率,如下式所示。这样改进可以提高算法的收敛效率,避免人工选择控制参数所带来的主观随意性,能够有效地克服未成熟收敛现象。

2.3 基于自适应遗传算法优化模糊BP神经网络算法

为了能够使评估预测的算法能够达到其最优化的性能并兼顾问题求解的不确定性和随机性,首先将模糊集合理论融入BP神经网络算法以解决问题求解的模糊性问题,同时采用遗传算法对BP神经网络的权值和模糊逻辑的隶属函数等进行优化,以提高BP神经网络的运行效率和收敛速度,最后通过将遗传算法进行多种群自适应性改进,解决遗传算法的未成熟收敛问题。通过算法的改进,能够使算法获得较好的运行效率和较好的评估预测能力,其具体执行流程如图4所示。

图4 改进遗传算法的模糊BP神经网络计算流程图

3 实例分析

3.1 设计网络结构

BP神经网络输入层和输出层神经元数目,是由输入和输出向量的维数来确定的。由炮兵火力运用方案的评估指标体系可知,输入层的神经元数目为8个。输出层表示炮兵火力运用方案的评估值,输出层的神经元数目为1个。对于模糊化层,设各个指标的模糊子空间为5,则模糊化层的神经元个数为40个。由于神经网络中模糊推理层的节点个数的确定是一个很复杂的问题,目前还没有明确的、统一的解析式,通常的做法是根据经验公式来具体地计算并确定出神经网络中模糊推理层的神经元个数,本文采用n≤n1+1,其中n为模糊推理层神经元个数,n1为模糊化层神经元个数,取n=n1+1=26。

3.2 选取学习速率和目标精度

在神经网络的拓扑结构确定之后,需要利用已有的样本数据在一定的学习规则约束下对神经网络进行学习训练来提高神经网络的适应能力。在神经网络的训练过程中学习的速率是根据经验和训练的稳定性来确定的,一般学习速率的取值是固定的,它的值也可以随着神经网络学习误差的变化而变化,一般学习率取值范围为(0,1),这里取学习速率的值为0.05。

神经网络是通过迭代更新的方法来确定神经网络各条连接神经的权值,因此神经网络的训练需要设定一个权值初始值。初始权值和阈值一般是随机确定的,它的取值会影响到神经网络的学习性能,通常将其确定为一个较小非零随机值,通常取值范围为(-2.4/F,2.4/F),其中F为神经元权值输入端所连接的神经元的数量。误差精度是指训练神经网络适应能力的精度标准,当误差达到该精度,则表示训练神经网络达到训练要求,可以停止训练,这里取值0.0001。

3.3 改进遗传算法优化权值和阈值

在建立了8-25-26-1的四层神经网络结构后,设置了神经网络的初始权值、阈值、学习速率等,根据如图4所示的改进遗传算法优化BP神经网络的流程,在神经网络中还需要设置对神经网络训练效率具有重要影响的初始权值和阈值等。根据遗传算法的参数设置,有初始的种群大小为NID=40,子种群的数量为NCD=4,遗传的最大代数为MAXG=50代,初始交叉概率Pci=0.7,初始变异概率Pmi=0.01,选择概率为SAP=0.9,交叉概率变化范围为(0.65,0.85),变异概率变化范围为(0.005,0.025)。由于输入神经网络的权值个数为702个,推理层的阈值为26,且推理层同输出层的连接权值个数为26,输出层阈值为1,因此将权值和阈值的二进制编码长度定为10位。

3.4 结果分析

程序的设计在Matlab2013a中进行,基于Matlab中模糊工具箱和神经网络工具箱,并采用谢菲尔德遗传算法工具箱编写改进模糊BP神经网络算法。根据以往评估数据作为本次评估算法的样本数据和测试数据,具体的指标数据值及其样本方案的评估值见表1。

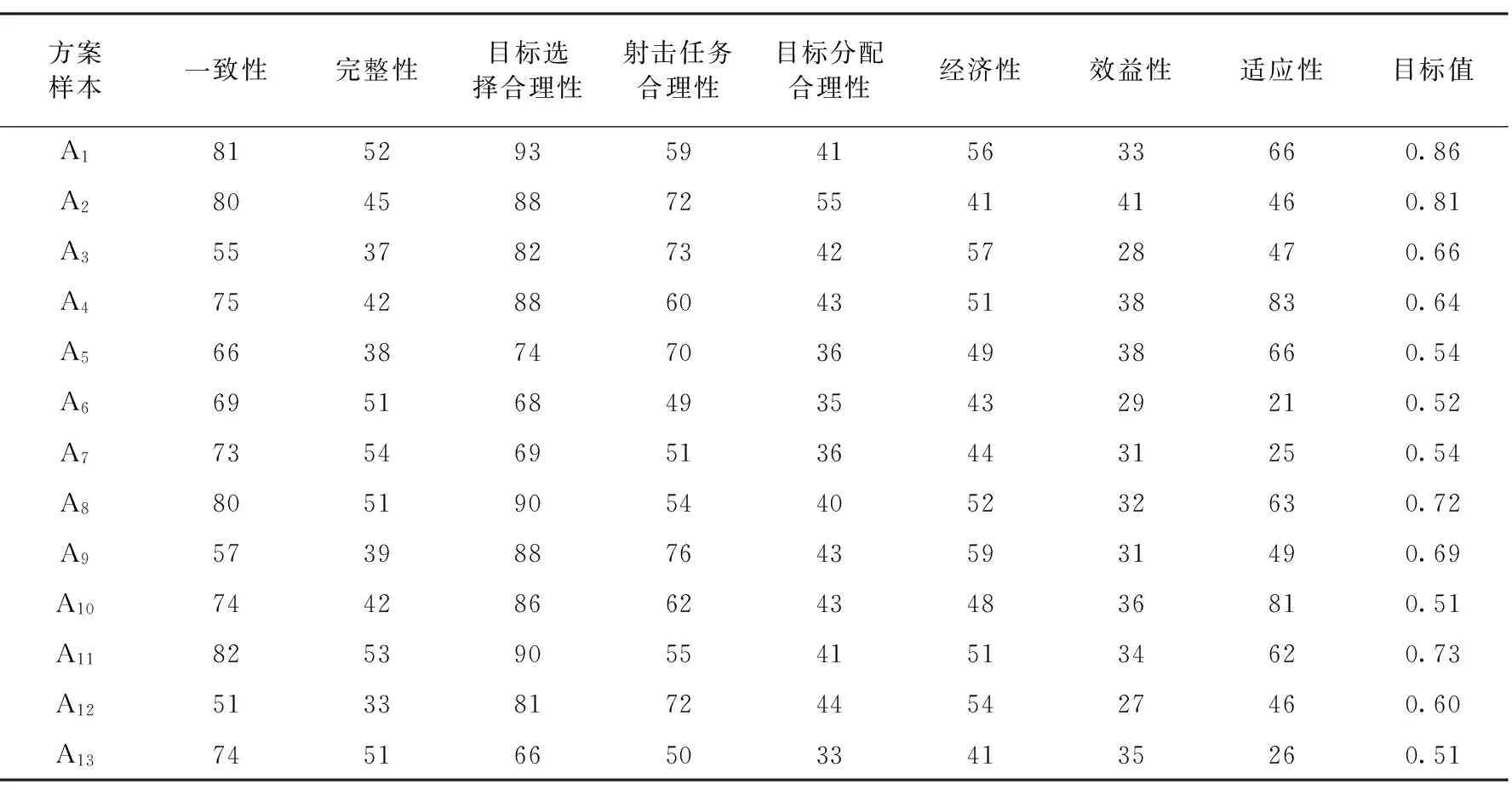
表1 样本的指标值及方案评估值

图6 改进遗传算法运行4次的进化过程图

分别运用遗传算法优化神经网络和改进遗传算法优化神经网络,得到如图5、图6所示的进化过程。

可以看出,遗传算法很不稳定,在500代时仍然没有完全稳定下来,而改进遗传算法则在41代时4次运行结果就完全一致,最优值为1.5394e-05,收敛速度快。可见,改进遗传算法利于进行BP神经网络的权值和阈值的优化处理。

将样本数据分别代入模糊BP神经网络、遗传算法优化的模糊BP神经网络、改进遗传算法优化的模糊BP神经网络可以得到如图7-9所示的神经网络误差收敛曲线。

图7 未优化BP神经网络误差收敛曲线

图8 遗传算法优化BP神经网络误差收敛曲线

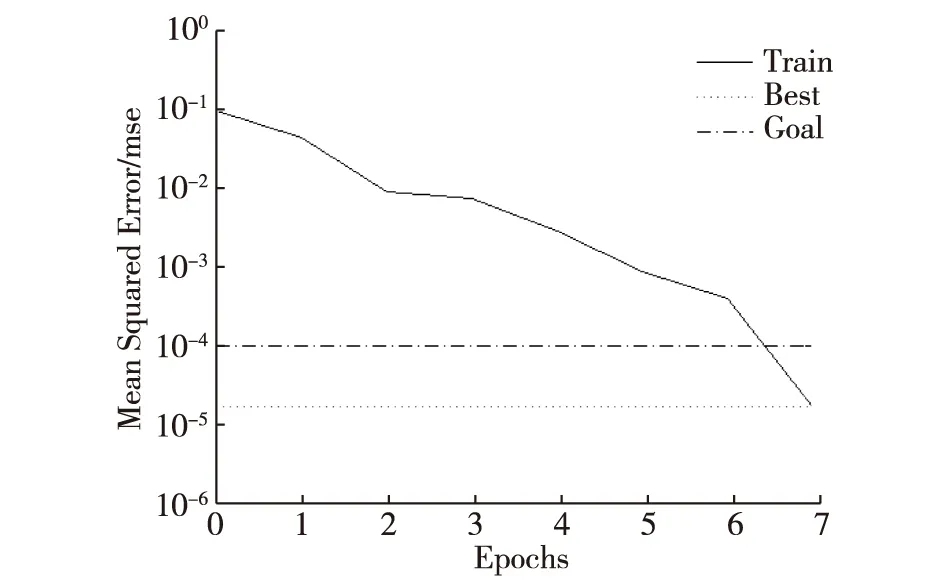
图9 改进遗传算法优化BP神经网络误差收敛曲线

分析可知,通过遗传算法和改进遗传算法优化的BP神经网络收敛速度更快,均在10代以内收敛,并且改进遗传算法相对遗传算法收敛速度有所提高。总体来看,改进遗传算法更加稳定可靠,对BP神经网络的优化效果更加明显,这说明通过改进遗传算法优化的BP神经网络算法能够对炮兵火力运用方案进行有效可靠地评估。该方法同样适用于各类作战方案的评估工作,能够提供有效的理论支撑。

设有三个炮兵火力运用方案,分别为B1,B2,B3,它们的指标值如表2所示。

表2 备选方案指标值

将三个方案的指标值分别通过改进遗传神经网络n=5次评估运行后,其结果如表3所示。

表3 方案结果

由表3可以看出,B2为最佳方案,B1为次优方案,B3为最劣方案。

4 结束语

人工神经网络具有天然的分布式信息存储和并行计算能力,从而提高网络的容错性和鲁棒性,是处理复杂的非线性问题的有效工具。目前,将人工神经网络同模糊系统、遗传算法等机制结合,成为研究人工智能并通过人工智能解决实际问题的一个重要方向。文中通过建立改进的模糊BP神经网络模型对炮兵火力运用方案进行评估,对评估中的复杂非线性问题有独特的优势,较好地克服了在评估过程中的模糊性和主观性的问题,为下一步研究炮兵火力运用方案评估问题提供了新的参考和科学的理论指导,同时也可以为实际作战和训练中炮兵火力运用方案的评估提供借鉴。

[1] 彭博,许劲松,刘开刚.基于三标度层次分析法的炮兵火力计划方案评估与优选[J].四川兵工学报,2010,31(8):119-122.

[2] 宋占岭,王亚莉.炮兵火力计划方案优选的模糊物元理想解模型[J].四川兵工学报,2011,32(12):128-130.

[3] 袁宏伟,张杨.灰色局势决策理论在炮兵火力计划优选中的运用[J].指挥控制与仿真,2008,30(6):29-31.

[4] 杨宇飞,汪洋,许劲松.基于灰色局势决策的炮兵火力计划方案优选[J].舰船电子工程,2010,30(9):62-64.

[5] 黄贡献,王晓兵,汪运禄.利用灰色局势决策法优选炮兵火力方案[J].兵工自动化,2012,31(2):31-33.

[6] 李杰,秦喜庆,尚保禄，等.基于神经网络的炮兵火力计划评估与优选研究[J]. 舰船电子工程,2012,32(4):28-29.

[7] 熊志斌.基于自适应遗传模糊神经网络的信用评估建模[J].系统仿真学报,2011,23(3):490-496.

[8] 周文明,范踊跃,宋吉星，等.基于遗传神经网络算法后勤指挥决策能力预测[J].火力与指挥控制,2015,40(7):51-56.

Assessment of Artillery Fire Application Plan Based on Improved Fuzzy BP Neural Network

LIU Tong1, LI Xiao-quan1, WANG Yong-liang1, WANG Jian2

(1.Nanjing Artillery College, Nanjing 211132;2.Unit 65565 of PLA, Dandong 118105, China)

To solve the subjection and uncertainty problems in the assessment of artillery fire application plan, the fuzzy theory is used in the BP neural network to assess them. The multiple population self-adaptive genetic algorithm is used to optimize the neural network to improve the efficiency of assessment. The index system, process and the model of the artillery fire application plan assessment are structured. In the final, an example is given to set up an analysis of simulation and validation, which proves an liable result and provides an effective way to assess the artillery fire application plan.

artillery fire application plan; assessment; neural network; fuzzy theory

2016-11-26

国防预研基金项目

刘 铜(1987-),男,重庆铜梁人,硕士研究生,研究方向为军事运筹学。 李小全(1976-),男,副教授,硕士生导师。 王永良(1964-),男,教授,硕士生导师。 王 键(1986-),男,参谋。

1673-3819(2017)01-0025-05

TJ810.3+7；E917

A

10.3969/j.issn.1673-3819.2017.01.006

修回日期： 2016-12-01