基于多尺度融合插值算法的风资源监测方法

蒋何++沈润杰++陈将威

摘 要 在可持续发展的背景下，风力发电规模迅速增大，风电基地占地面积迅速扩大，导致风资源监测愈发困难。原有的测风塔已很难满足对大型风电基地中细节风速分布的监测，为风电场运维管理带来一定困难。本文主要研究一种多尺度风资源立体监测网络。

【关键词】风资源 多尺度 数据融合 大型风电基地

1 引言

风力是风力发电的基础，对风电场风资源分布的有效监测是风电场理论出力评估和预测准确性的保障。过往的风电场中简单利用少量几个测风塔监测整个风电场的风资源情况，在大型风电基地中会导致风电场群内部大部分区域的风资源情况与实际情况存在一定误差，对风电场发电分析造成很大的影响。为解决上述问题，本文提出了风电场风资源多尺度立体监测网络。

为更好地实现对大型风电基地的风资源监测，建立了基于测风塔、风机机头监测系统及雷达的多尺度立体监测系统。

根据侧风塔数据、风机机头数据、雷达测量数据、地形数据、天气数据等环境因素，利用多时空尺度的融合插值等算法，对大型风电基地整体风场进行模拟分析，构建环境因素在实际风机位置点的插值模型。风电基地监测环境构架如图1所示。

2 并行多尺度数据融合

风资源多尺度立体监测系统是一个较简单的分布式检测系统，三种类别的监测节点使用不同的监测方法、原理和装置，所以在集中分析之前会分别对三种类型的监测数据进行预处理，例如数据最优局部处理和融合处理等，以减小多尺度分布式监测系统的性能损失。

2.1 检测级融合并行结构

并行结构分布式监测系统结构如图2所示，当三种类型的监测节点收集到未经处理的原始数据，需在各自的分处理中心作出局部检测判决等处理；最后，监测中心对所有集中后的数据进行融合处理，得到相应的全局数据。

2.2 基于并行结构的数据融合算法

在并行结构局部判决融合处理中，使用贝叶斯假设检验获得极小化系统运行的平均代价R（Γ），其判决规则集合为Γ={γ0，γ1，L，γN}，其中γ0表示融合规则，γ0（g=1，2，L，N）代表局部检测的判决规则。

新的融合估算值基于以前的融合估算以及新的测量值，小波变换被用来连接不同尺度之间的测量数据。该算法对于多尺度数据滤波融合是很有效的。

4 基于多尺度数据的Kriging插值方法

经多尺度数据融合处理，几种采集时间间隔不同、范围不同的数据被融合为相同时间、空间刻度上的数据，并得到插值方法所需要的风资源基础数据。大型风电基地地形较为复杂，Kriging插值在该类三维空间插值分析中得到了广泛的应用。

4.1 时空协方差函数

时空域随机过程满足二阶平稳或固有假设时，其协方差函数可表示为：

式中，U（s，t）表示定义在时空域的随机过程，且U（s，t）∈Rk×T，其中Rk表示k维的欧氏空间，T代表时间；（s，t）为时空场中任意监测节点的位置，△s为监测节点空间中的距离，△t为时间上的距离。

同时，对应的变差函数可表示为：

实际中多采用简化的样本变差函数，如式（10）所示：

4.2 Kriging插值

Kriging方法假定采样点之间的距离和方向可以反映一些空间相关性，对周围的测量值进行加权分析得出未测量位置的预测，与反距离权重法类似。Kriging插值是一种线性的无偏估计，并且要求估计误差的方差最小。在风资源监测环境中，监测节点的空间位置是三维的，所以监测位置参数可表示为si={xi，yi，zi}，Kriging插值公式为：

式中，U*（s，t）为待测点（s，t）处的插值；λi为相应监测点的加权系数，当然应满足∑λi=1，该参数的计算式为：

5 实验结果

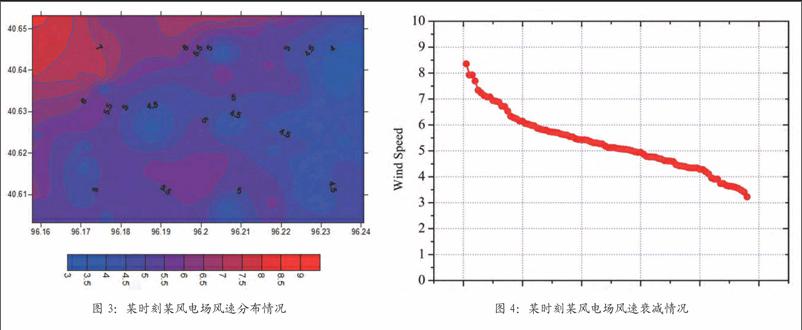
使用上述多尺度插值融合算法，基于某一时刻（2015年1月22日03时10分）雷达监测数据、风机机头处监测数据和测风塔测量数据，对某一样本风电场中的风速分布进行分析，整个风电场中的风速的分布情况如图3所示。从整体上可以看出，风电场上游为强风速区，下游为弱风速区；同时在距离上游一定的距离处，风电场中心的风速明显小于风电场边缘两侧的风速，一般风速差能达到1-2m/s。

选取该时刻该风电场的风场数据对整个风电场中风机尾流效应造成的风速衰减现象进行分析。如图4所示，对该时段整个风电场中所有风机的机头风速从大到小的排列，结果显示风速从上游风机机头风速的8.5 m/s 衰减为下游的3.2 m/s，风速下降率为62.4%。

6 结论

风资源立体监测网络使用多个尺度的监测数据对大型风电基地风资源进行监测，与过往单一的测风塔监测方法相比更能监测风电基地中风电群场内部细节处的风资源分布情况，使风资源监测的精度大大提高。

参考文献

[1]胡毅，张建.风资源评估中风速分布方法研究[J].内蒙古科技与经济，2010（12）：76-78.

[2]Yiahak Feliks，Ehud Gavze，Reuven Givati.Optional Vector Interpolation of Wind Fields.Journal of Applied Meteorology，1996，35：1153.

[3]王鹏伟，吴秀清，孙福明.基于多尺度Kalman数据融合滤波[J].光电工程，2008，35（01）：110-115.

[4]司长哲，任松.基于Kalman滤波的数据处理多尺度融合算法[J].计算机测量与控制，1999，25（05）：627-632.

[5]N.Cressie，G.Johannesson. Fixed rank kriging for very large spatial data sets[J].Journal of the Royal Statistical Society： Series B（Statistical Methodology），2008，70（01）：209-226.

[6]周彬彬，蔡建國，冯健.基于ARMA模型和时空Kriging插值联合模拟大跨结构的脉动风速时程[J].脉动与冲击，2014，33（03）：29-34.

作者简介

蒋何（1992-），男，四川省人。硕士学位。研究方向为控制科学与工程。

作者单位

同济大学电子与信息工程学院 上海市 201804