基于遗传算法的机舱管路自动布置研究

高跃峰+张均东

摘 要 船舶机舱管路分布密集、且走向复杂，目前在生产设计中仍然主要依靠经验丰富的专业人员来完成管路的布局。为实现船舶机舱管路的自动布置，基于遗传算法设计了一种自动寻找最优路径的算法。算法通过将机舱空间分割为三维网格节点，将各个坐标点编码，产生初始种群，建立个体适应度函数，根据路径总长、路径弯头数、路径能量值来评价个体的适应度，从而评价路径的优劣，从中选择适应度高的个体作为父代进行交叉变异，经过一定代数的遗传进化可使种群收敛到全局最优解，得到最优路径。仿真实验证明该算法在寻找最优路径方面可行、有效，并将其应用于虚拟船舶机舱视景仿真的管路布置设计中，对船舶生产设计中的管路布置有一定参考价值。

【关键词】船舶制造 机舱管路 自动布置 遗传算法

0 引言

船舶机舱是典型的复杂室内场景，舱内管路纵横交错，设备繁多，高效地管路布置是实现船舶设计制造和虚拟船舶机舱视景仿真的关键环节。机舱管路的布置是船舶制作设计中的重要一环，但由于机舱管路较为复杂，目前还主要依靠管路设计经验丰富的专业人员来完成，自动化程度较低，并且使船舶整体的设计周期延长。因此，在整个机舱管路设计中，自动化技术的运用对于提高船舶设计效率、降低设计成本具有重要的意义。

在实船中，对管路的布置和敷设必须要满足很多约束条件。在本研究中，认为对以下的几个条件是必不可少的：

（1）空间方面：所布置管路要能够自动避开机舱设备、管路及舱壁等。

（2）成本方面：所设计出的管路要求在经济方面达到最优，即在管路能够避开机舱设备的前提下，其总长度最短（耗费材料最少），管路的弯折次数即法兰数量最少。

（3）安装方面：管路应尽量贴舱壁或舱顶布置，不能离舱壁太远，同时应不出现斜管。

大部分文献在判断障碍物时采用在目标函数中加入罚函数法，这种一贯的做法表面上看能够剔除种群中适应度值较低的个体，但实际上在初始化种群时产生了很多非法个体；文献[3]的选择算子在利用最优保存策略时替换个体数量略少，算法参数选取所得结果并非最优。据此本文提出一种遗传算法，在初始化种群时采用逐点判断的方法来减少非法个体的产生，并且增加最优个体保存数量，将其用于船舶虚拟机舱的管路自动敷设，仿真实验证明该方法可行、有效。

1 遗传算法概述

遗传算法（Genetic Algorithm）是借鉴达尔文生物进化论中自然选择和遗传学原理来模拟优化计算的模型算法，通过不断进化逐渐搜索出过程最优解。遗传算法种群中的每一个体代表一个可行解，通过这些个体模拟自然界中生物染色体的交叉变异过程，产生新的种群，使个体的适应度值（优秀程度）越来越大，当进化到一定代数时，最佳个体被保留，即得到解决问题的最优解。

2 算法设计

2.1 管路编码设计

编码操作是运用遗传算法解决实际问题的重要一环，整个算法是否能够成功在很大程度上取决于编码操作。在本例中，用长方体空间来简化模拟实船机舱，并将其均匀切割为A×B×C个坐标的节点，每个节点的坐标即固定为（a，b，c），例如一个长、宽、高分别为1、2、3的长方体型三维空间，其总的节点数为24（2×3×4）个，节点采用十进制方式进行编码。在三维空间中，若给定起点和终点，那么能够连接这两个点的任意一条管路就是一个染色体，也就是一个个体，这个个体的基因即为其上的每个坐标点，在上例中管路{（0，0，0），（1，0，0），（1，0，1），（1，0，2），（1，0，3），（1，1，3），（1，2，3）}就是满足条件的种群中的一个个体（染色体），路径上的坐标点即为其基因。由于管路可能存在反复、回折等现象，因此对于符合条件的管路其长度是不确定的，这就导致每条染色体上的编码长度不一定，因此必须采用变长度的编码方式进行编码。在实际编码中，管路节点从起始点出发，每次前进一个节点，直至到达终点，为了避免产生斜线，下一个节点的坐标只能与上一个坐标在某一个坐标轴上相差1，比如前一个节点坐标为（i，j，k），那么后一个节点坐标就必须为（i+1，j，k），（i-1，j，k），（i，j+1，k），（i，j-1，k），（i，j，k+1）和（i，j，k-1）中的一个，使用这种策略得出的管路可使其路径任意一段始终平行于长方體空间的棱。

2.2 种群的初始化

所布置管路构成的种群初始化就是指在整个算法的起始随机生成多条满足条件的路径，这些路径都能够从起始点到达终止点。但如果缺乏导向，管路在机舱三维空间的移动就具有相当大的随机性，这会导致管路在空间中出现折返、交叉等现象，与实际不相符合，为避免这种情况发生，在使用算法搜索路径时，若管路是向终点方向移动，那么规定此时向这个方向移动的概率将大大超过向其他方向移动的概率，使用这种方式可使种群中优良个体的比例大大提升。

管路按照概率大小由起始点向终止点移动，每相邻两个节点的距离为1，此时初始化生成的种群中一定有许多管路穿越障碍物，不满足要求。文献[3]在解决此问题时采用了罚函数的办法，当生成的管路穿越障碍物时，立即将此管路的适应度值将至最低，而此个体由于适应度较低无法进入下一代，这种办法有效但带来的后果是使种群中生成的有用个体减少，并且使整个算法的计算效率下降。所以本文在初始化种群个体过程中，管路在由上一个节点向下一个节点移动时，则判断下一个节点是否在障碍物中，若在则直接将此点剔除，重新向其他方向移动，而这点是一定存在的，若这点不在障碍物中则继续向下一点搜寻，直至完成管路的初始化，使用这种办法得到的个体一定是已经避开障碍物的管路。

另外，在初始化过程为避免管路折返，特采用截断机制，如初始化可能生成回路如（0，0，0），（0，0，1），（0，0，2），（0，1，2），（0，1，1），（0，0，1），（0，1，1），采用截断机制后直接简化为（0，0，0），（0，0，1）， （0，1，1）。

2.3 目标函数和适应度函数的设计

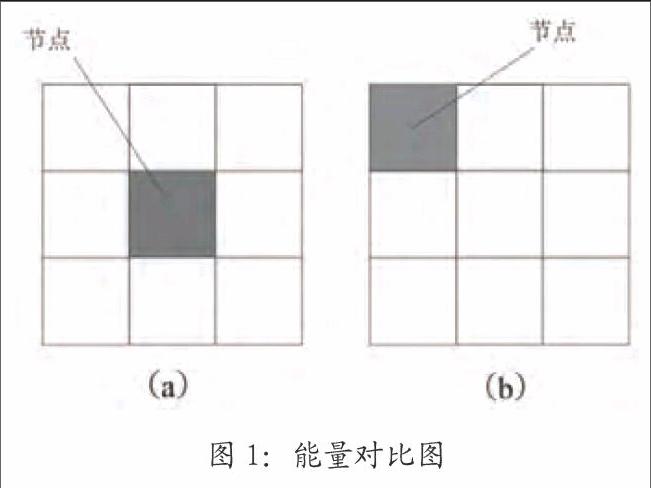
在设计初期，需要对障碍物模型进行简化，将机舱简化为立方体空间，设备、已有的管路等障碍物简化为长方体空间。引言中的（1）条件已经在种群的初始化中实现，对于条件（2）可以通过编程时计算和比对坐标实现管路总长度和弯头数的统计；对于条件（3），本文引入能量值的概念，也就是将空间各个节点赋予一定的能量值，搜索管路的过程也就是将所经过的节点能量值累加的过程。规定距离舱壁近的坐标点能量值低，而距离舱壁较远的坐标点则能量值较高，规定能量较低的个体适应度高，这样即可使所产生的管路个体大部分为贴舱壁布置。在图1中（b）节点较（a）节点离舱壁更近，故其能量值较低，经过该节点的个体由于适应度值较高而易于保留并进入下一代种群。本文使用E（r）表示管路总的能量值，在不断的进化过程中使E（r）值最低，从而使管路尽量贴舱壁布置。

综上所述本文中遗传算法的目标函数取为式（1），适应度函数可取为式（2）或式（3）。

表示一条管路的总长度，l（nodei，nodei+1）表示管路路径中相邻两个节点之间的距离，在本文中都为常数1；B（r）表示管路路径总弯头数；E（r）为所得管路的能量值；其中，A为适当大的正常数，需保证F（r）的取值为非负数；a，b，c均为正常数系数。

2.4 选择算子的设计和改进

本文结合排序选择思想和最优保存策略思想，在进化过程中首先将种群的所有个体按照适应度的大小由高到低依次排列，然后将适应度最高的3个个体替换适应度最低的3个个体，种群中其他个体保持不变，这样一方面可以保留比较优秀的个体，另外也不会使部分个体在早期就占据全部种群空间，从而保持了种群多样性，避免了遗传算法中“早熟”的现象发生。算法的整个选择过程如图2所示。

2.5 交叉与变异算子的设计

在本算法中，染色体为所生成的管路，基因则为管路上的各个坐标点，个体的杂交就是各自染色体的配对和交叉，本算法采用基本的随机组合杂交策略，也就是将初始化产生的全部个体两两配对，经过交叉遗传产生2个新个体。本算法由于其特殊性必须采用十进制进行编码，因而交叉操作也基于十进制完成，经过试验，算法运用交叉点杂交结合随机点杂交来完成染色体的配对。杂交原理如图3和图4所示。

文獻[3]采用交叉点杂交和随机点杂交结合的办法，但并未详细说明种群何时以及如何采用交叉点杂交，文献[4]只探讨了随机点杂交，这样在一定程度上降低了种群的多样性。本文基于文献[3]和文献[4]设计出改进的杂交算子，将两种杂交方式相结合，在开始进行交叉操作时就将每条管路上的坐标点（基因）进行一一比对，如果有相同坐标，则采用交叉点杂交办法进行杂交，如果有多个相同的坐标点，就多次运用交叉点杂交操作，生成一对新的个体，运用这种办法可能在一定程度上降低了程序的运行效率，但可使种群的多样性大大增加，对最终产生符合条件的个体非常有利。另外，产生的子代个体中还有可能出现管路坐标点相同的情况，此时依然采用截断策略来对个体进行保留。

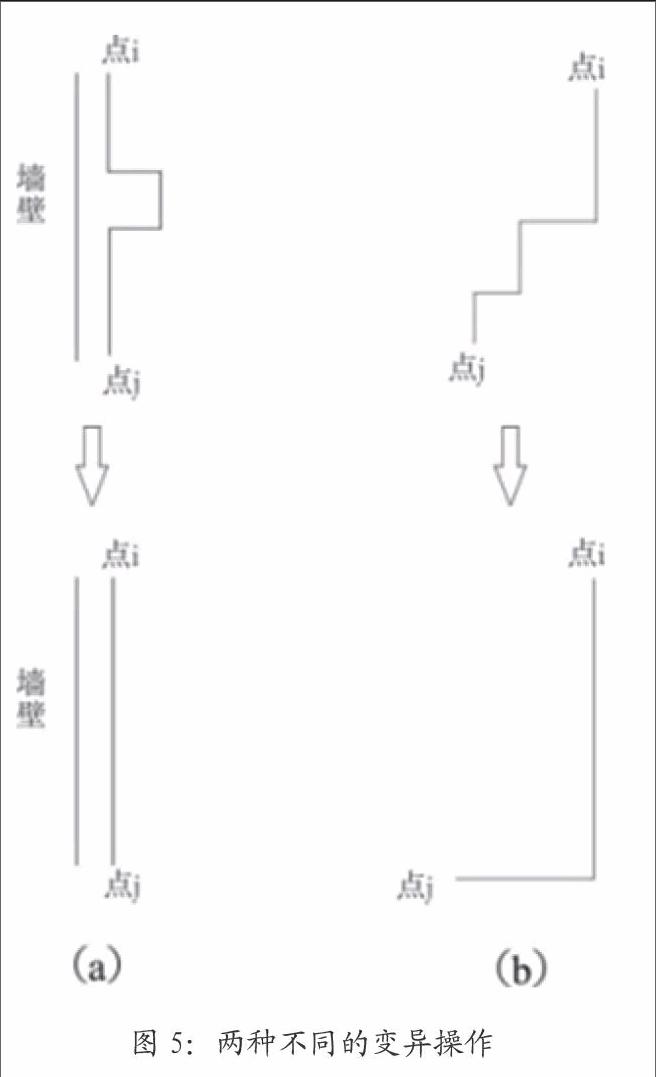
为了尽量减少遗传算法的局部收敛现象，本文采用如图5的贴墙壁操作和去弯头操作来实现变异操作，从而对个体的基因进行局部改造。

图6为运用遗传算法解决管路自动布置问题完整的流程图。

3 仿真实验

本文在Windows7环境下，用MATLAB R2013a软件实现遗传算法应用与船舶管路布置的仿真实验，并分析其结果。本文使用相对顶点坐标为（0，0，0）和（30，30，30）的立方体来模拟船舶的机舱三维空间，在其中设置3个长方体障碍物用来模拟机舱中的设备或管路，使用相对顶点坐标为（0，15，0）和（5，25，25）的长方体来模拟第一障碍物，用相对顶点坐标为（25，0，0）和（30，5，30）的长方体空间来模拟第二障碍物，使用相对顶点坐标为（10，25，25）和（20，30，30）的长方体来模拟第三障碍物。为了简化，规定机舱空间的相对顶点为所布置管路的路径起始点和终止点，即（0，0，0）为管路布置的起点，（30，30，30）为管路布置的终点，整个模型空间如图7所示。

在遗传算法解决实际问题的过程中，参数的设定会对算法的性能产生较大的影响，这些参数包括种群大小、进化代数、交叉概率和变异概率等。但到目前为止还没有定论能够指导如何选择合适的参数能够使算法最优，在解决实际问题中基本还依赖前人的经验和大量的重复试验。

本文在已有文献基础上进行了大量的试验，确定了能够使结果达到最优的参数，规定初始化产生种群中的个体数量为300个，使其进化完成交叉变异过程120代，即种群进行120次的交叉变异操作，交叉的概率经过试验0.7为最优，变异操作由于视情况不同故不设定变异概率；另外设定其他参数A=1000，a=0.004，b=0.005，c=0.003。

通过计算机仿真实验计算100次后，产生的种群中个体大部分管路总长度为90左右，总的弯折数（即法兰数）在10个上下，从中选出一条各方面均较为满意的管路为{（0，0，0），（0，2，0），（0，2，30），（0，3，30），（7，3，30），（7，15，30），（16，15，30），（16，23，30），（28，23，30），（28，30，30）， （30，30，30）}。该管路的总长度为90，总弯头数为9。图8展示了该管路路径的三维空间走向。从图中可以看出，该管路基本满足了我们的各项需求，总长度最短，弯头数最少，并且能够避开空间内的多个障碍物，也基本能够贴舱壁布置。但经观察后发现，管路在几个位置存在连续弯折两次的问题，这是遗传算法的特性使然，此时需要对所得管路进行适当的微调，使其更加符合要求，将其调整为如图9的{（0，0，0），（0，2，0），（0，2，30），（7，2，30），（7，23，30），（28，23，30）， （28，30，30），（30，30，30）}，这条管路的总长度仍然没有变化，但管路总的弯折数（法兰数）减少至6个，经济性更加良好，也使管路的走向更加美观。在解决实际问题时，自动化的算法设计出的管路能够为我们在机舱管路布置中提供一定的导向作用，但由于算法本身存在一定随机性，导致生成的管路难免会有不合理或不经济的情况，那么这时候船厂的技术人员可适当对生成的管路进行微调，使其更加满足需求。

算法运行结束后，运用MATLAB分析整个算法的进化过程，图10为最终生成的所有管路的适应度值，其按照由高到低排列，可以看出在最终产生的种群中大部分个体的适应度值都能接近最大值，其中最高的适应度值为999.7。

图11与图12为运用该算法时个体适应度值随遗传进化代数变化的趋势图，从图中可以看出，该算法在进化到约80代左右时实现收敛，收敛时的迭代时间大约8分钟左右。

将该算法应用于虚拟船舶机舱视景仿真中，同时对多条管路进行布置，实际证明取得了良好的效果，能够避开障碍物，并且使管路长度较短，同时也节约了管路布置的时间，图13为该算法应用于30万吨VLCC虚拟船舶机舱管路布置的实际效果图。

4 结论

本文着重研究了一种基于遗传算法的船舶管路自动布置方法，在一定的立体空间内，将染色体的编码、选择、交叉和变异操作应用于船舶管路的节点连接，自动寻找出一条能够避开障碍物，不走斜线，尽量贴近墙壁，且管路总长度和弯头数最少的路径。

经过仿真实验表明：算法切实有效可行，能够在初始化时即排除进入障碍物的个体，最终基本生成符合条件的管路路径，操作简单方便，外加对管路适当地微调，能够使管路的路径完全符合实际的要求。这种方法再经更深入的研究和推广后，能够应用于船厂的管路布局设计环节，从而提高船舶的设计效率。

参考文献

[1]曾鸿，任光，苏玉龙.虚拟船舶机舱场景中的快速自动漫游算法研究[J].大连海事大学学报：自然科学版，2012，38（04）：39-42.

[2]鄒玉堂，任光，路慧彪.船舶管路布置仿真模型简化[J].上海海事大学学报，2010，31（01）：72-76.

[3]白明.船舶管系路径优化算法研究[D]. 哈尔滨：哈尔滨工程大学，2010，45-65.

[4]刘少卿.基于维修性的船舶管路布局优化研究[D].武汉：武汉理工大学，2010：20-52.

[5]姜银焕.基于遗传算法的液压支架管路优化布置[J].煤矿机械，2013，34（11）：24-25.

[6]沈龙泽，刘衍聪，王文超，等.海洋石油平台自动化管路布局优化算法设计[J]. 石油机械，2014，42（02）：34-39.

[7]卢永进，华志刚.基于FORAN的船舶管路三维设计研究[J].船海工程，2012，41（05）：77-80.

[8]贾金，宋永庄， 张闯，等.船舶管路综合布局优化[J].科技资讯，2013（23）：90-90.

[9]闫兴亚，吴加贺，石云平.基于遗传算法的虚拟校园漫游路径规划[J].西安邮电大学学报，2013，18（06）：80-84.

[10]赵柏萱，宁汝新，刘检华.虚拟环境下的管路布局与装配仿真系统关键技术[J].北京理工大学学报，2010，30（08）：895-900.

[11]范小宁.船舶管路布局优化方法及应用研究[D].大连理工大学，2006.

[12]Wang Y，Wang C，Peng F，et al. Intelligent layout design of ship pipes based on genetic algorithm with hu-man-computer cooperation[J].Ship Building of China，2015，56（01）：196-202.

[13]Ito T.Genetic algorithm approach to piping route path planning[J]. Journal of Intelligent Manufacturing， 1999，10（01）：103-114.

作者简介

高跃峰（1989-），男，山西省忻州市人。硕士学位。现为大连海事大学轮机工程学院实验教师，助理实验室。主要研究方向为轮机工程。

张均东（1967-），男，浙江省金华市人。博士学位。现为大连海事大学轮机工程学院教师，教授。主要研究方向为轮机自动化与智能化。

作者单位

大连海事大学轮机工程学院 辽宁省大连市 116026