基于Reflected Sigmoid激励混沌神经元的图像加密技术研究

◆许 楠 李树政

基于Reflected Sigmoid激励混沌神经元的图像加密技术研究

◆许 楠1李树政2

（1.黑龙江八一农垦大学信息技术学院 黑龙江 163319；2.黑龙江省大庆市红岗区信息中心 黑龙江 163000）

选取径向基函数的一种即Reflected Sigmoid函数作为激励函数构建了混沌神经元新模型，通过神经元倒分岔图像以及最大Lyapunov指数的分析，说明该模型具有混沌动力学特性。当撤销模拟退火策略的作用后，通过对几个重要的混沌时间序列参数的考查，证明该新型神经元动力系统可以永久处于混沌搜索状态不变；利用混沌与密码学的相关特性，将该模型应用于图像加密，说明了密钥产生的方法及过程，通过观察直方图是否分布均匀，体现该混沌加密算法的抗统计分析能力。

Reflected Sigmoid函数；动力学特性；时间序列；统计分析

0 前言

混沌理论上述诸多特点与密码学的很多要求都是相互吻合的，正因为这样的密切联系，所以混沌密码学得到了越来越多的关注以及研究，本文将Reflected Sigmoid激励混沌神经元模型与图像加密相结合，对其加密可能性以及加密效果进行阐述。

1 Reflected Sigmoid激励混沌神经元动力系统

1.1 Reflected Sigmoid激励混沌神经元模型

选取对称的Reflected Sigmoid函数（它是径向基函数的一种典型函数）作为激励函数，构建一种新型简称“Reflected Sigmoid激励混沌神经元模型”，可以表示为:

其中x（t）为激励函数，这里采用的是Reflected Sigmoid函数，δ为径向基函数的宽度系数；I0为一正参数；y（t）为神经元的内部状态；k的取值范围为0≤k≤1，称为神经隔膜阻尼因子，k越大说明网络保留内部状态的能力越强，k越小网络遗忘内部状态的能力越强；z（t）称为自反馈连接项，它是不断衰减的，采用模拟退火策略控制其变化的快慢；β是模拟退火参数。

1.2 Reflected Sigmoid激励混沌神经元模型的动力学特性分析

通过上图不难看出:β值越大收敛速度越快，混沌搜索持续时间较短，容易陷入局部极小点，而无法找到全局最优解；而β值越小收敛速度越慢，混沌搜索持续时间较长有利于跳出局部极小点的限制，找到全局最优解。

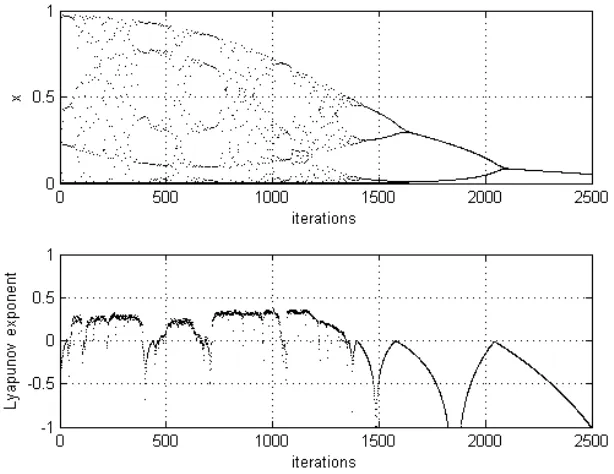
图1 时神经元倒分岔与最大Lyapunov指数演化图

图2 时神经元倒分岔和Lyapunov指数演化图

通过Lyapunov指数演化图可知:该神经元模型采用模拟退火策略，逐步消除混沌搜索过程，当倒分岔图形收敛到平衡点的时候，系统达到稳定状态，此时体现在图中的Lyapunov指数值稳定在0值左右。

1.3 永久保持混沌搜索的Reflected Sigmoid激励混沌神经元动力系统

将Reflected Sigmoid激励混沌神经元的模拟退火策略去除，即将原公式（3）去掉，公式（2）改为以下公式（4）:

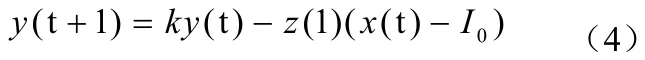
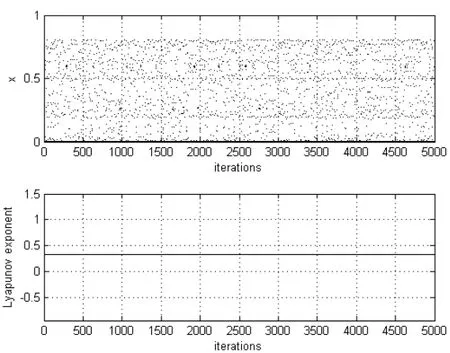
图3 永久保持混沌搜索的Reflected Sigmoid激励混沌神经元状态图

从图3看出，在没有采用梯度下降策略[2]的情况下，Reflected Sigmoid混沌神经元系统永久处于混沌搜索状态，而不能收敛到稳定的平衡点，没有产生倒分岔过程，这样前面的假设就可以得到了证实。

图4 高斯激励混沌神经元的功率谱

该高斯激励混沌神经元系统的功率谱无明显的峰值，而且峰值连成一片，出现“宽锋”是系统处于混沌状态的重要依据，由此证实系统能够永久保持混沌搜索状态不变。

图5 混沌时间序列的关联维

图中存在直线的区域，说明此区域内客体具有自相似性[4]，即局部的结构或功能与整体相似，可视为“分形”，分形理论可对混沌吸引子的结构和形态进行刻划，由此说明该神经元系统能够永久保持混沌状态不变。

2 图像加密

2.1 混沌加密原理及加密算法

基于ReflectedSigmoid激励混沌神经元系统的图像加密算法[5]的具体过程可以描述如下:

（1）对原图像各像素点的明暗程度进行量化，将原始图像按照分辨率转化为M行N列的二维矩阵，如公式（5）所示:

（2）将上述的永久保持混沌状态的Reflected Sigmoid激励混沌神经元模型作用于原图像矩阵，由此可以将密钥映射为二维混沌序列，模拟实验参数初值情况为:，其中key为根据实际图片确定的辅助密钥；

（3）加密因子序列是通过将混沌序列映射到0～255的8位二进制整数序列得到；

（4）将原图像矩阵各元素值同加密因子序列按位进行异或运算，从而得到加密图像的各像素加密值；

（5）加密后的图像由公共通道输出。

利用上述方法对原图如图6所示进行加密，加密后图像如图7所示。

此次加密过程是成功的，加密后的密文图像没有体现任何明文图像信息，仅仅是杂乱无章的黑白图像，满足的扩散和混乱的效果，可以说明通过此新模型构造的加密密钥，能够有效的应用于图像加密过程。

图6 原始图像

图7 加密图像

2.2 统计性能分析

图8是明文图像灰度值的柱状分布图，可以看出该图重点体现了原图像的中间色调信息，而且分布不均匀；而图9是密文图像的直方图，可以看出无论是阴影、中间色调及高亮信息都很均匀，0～255各个像素值出现的次数都在600～1000之间，这表明了该混沌加密序列将明文图像有效的掩盖，而且具有较强的抗统计分析能力。

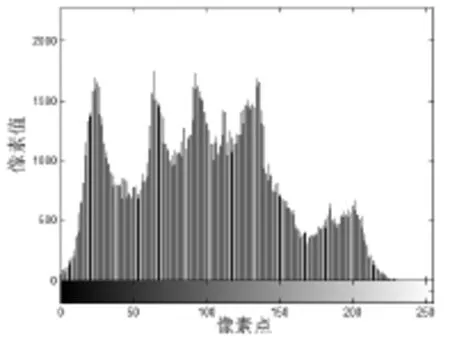
图8 明文图像的直方图

图9 加密图像的直方图

3 结束语

采用单一的Reflected Sigmoid函数作为激励函数，构建一种新型的混沌神经元模型[6]，通过对时间序列特征量的考查，验证了它永久保持混沌搜索状态的可行性；利用该新模型生成二维混沌序列，通过异或运算对灰度图像进行加密，通过仿真实验证实此方法的可行性，通过对明文密文的直方图的考查，说明了该算法具有较强的抗统计分析的能力。

[1]许楠，宁常鑫，徐耀群.一种径向基混沌神经网络分段退火策略及应用[J].计算机应用与软件，2014.

[2]杨涛，刘文杰，丁宁.基于梯度下降算法的神经网络模型研究[J].网络安全技术与应用，2013.

[3]王福杰，潘宏侠.MATLAB中几种功率谱估计函数的比较分析与选择[J].电子产品可靠性与环境试验，2009.

[4]王江涛，杨建梅.复杂网络的分形研究方法综述[J].复杂系统与复杂性科学，2013.

[5]刘乐鹏，张雪峰.基于混沌和位运算的图像加密算法[J].计算机应用，2013.

[6]Controlling Chaos in Neuron Based on Lasalle Invariance Principle[J].Communications in Theoretical Physics，2011.

2016年黑龙江省大庆市指导性科技计划项目，项目编号:zd-2016-012。