村镇生活垃圾中转站选址优化研究*

李倩茜，马慧民，陈一军，毕珠洁

（1.上海市市容环境质量监测中心，上海 200085；2.上海电机学院商学院，上海 201306；3.上海市环境工程设计科学研究院有限公司，上海 200232）

村镇生活垃圾中转站选址优化研究*

李倩茜1，马慧民2，陈一军1，毕珠洁3

（1.上海市市容环境质量监测中心，上海 200085；2.上海电机学院商学院，上海 201306；3.上海市环境工程设计科学研究院有限公司，上海 200232）

针对村镇生活垃圾收运系统中中转站选址问题，从垃圾收集系统总费用、中转站个数及规模、中转站服务范围、中转站建设对居民区产生的环境负效应等方面考虑，以成本最小、环境负效应最小为目标函数建立了多目标规划模型，并以上海市青浦区部分村镇为例，运用遗传算法进行求解。

村镇生活垃圾；选址；遗传算法

1 村镇生活垃圾中转站选址优化模型

1.1 问题提出

长期以来，国内在对生活垃圾管理系统的研究上［1-4］，主要集中于生活垃圾的末端处置，对生活垃圾收运系统的研究比较滞后。本研究主要考虑村镇生活垃圾中转站的选址问题，在垃圾收集点及垃圾处理场的位置和数量确定的情况下，垃圾收运过程中所有的费用与垃圾中转站的位置及其规模有关。同时，中转站如果离居民区太近，可能会影响到周围村民的身体健康，若中转站离居民区过远，又会导致垃圾运输成本增加。因此，本研究建立了一个双目标动态规划模型，通过最小化经济成本和中转站对居民区产生的负效应，从而确定建立中转站的最合适选址、容量以及服务等范围。

1.2 模型建立

关于环卫设施建设风险的度量方法，国内外的许多学者已经做了相关的研究，Erkut和Neuman［5］提出风险的度量方式可用（S）ip（di）jq来表达，Si表示污染源i所包含的污染物总量，dij表示污染源i与居住区j之间的欧氏距离。Melachrinoudis等［6］指出，污染物不均地向周围各处扩散，因此提出了污染扩散因子的表达式为，其中，dij表示污染源i与居住区j之间的欧式距离，θij是指污染源i与居住区j之间连线与x轴的夹角，φi是指污染源i中的污染物最大扩散方向与x轴间的夹角。

1.2.1 模型假设

为方便说明问题，对村镇生活垃圾中转站选址问题作如下假设：①所有垃圾中转站备选点已通过某些重要指标的论证，且符合相关法律法规；②新建垃圾中转站仅在已知的备选点中选择；③中转站建设费用、生活垃圾单位运输费用已知；④生活垃圾总运输费用与垃圾运输距离及垃圾运输量成简单线性关系；⑤计划期内居民人口数与各垃圾收集点垃圾量是确定的，并在一定时期内保持不变。

1.2.2 参数和决策变量

1） 下标：i为垃圾收集点（即居民区） 集合i∈{1，2，…，I}；j为中转站备选点集合j∈{1，2，…，J}；m为中转站容量等级集合m∈{1，2，…，M}；k为垃圾处理厂集合k∈{1，2，…，K}。

2）参数：Fjm为在中转站备选点j建设m容量等级的中转站所需的固定成本（元）；T为中转站计划运营年限（a）；t0为中转站建设期（a）；r为现值转化贴现率；Vjm为在中转站备选地j建设m容量等级中转站所需的年运营成本（元）；Cij为从垃圾收集点i到中转站j的单位垃圾量单位运输距离的运输费用（元/（t·km））；Di为垃圾收集点所产生的垃圾量（t）；dij为垃圾收集点i到备选中转站j的距离（km）；djk为备选中转站j到垃圾处理厂k的距离（km）；Bjk为从备选中转站j到垃圾处理厂k单位垃圾量单位运输距离的运输费用（元/（t·km））；qj为备选中转站j的负效应指数；θij为备选中转站j与垃圾收集点i之间连线与x轴的夹角；φj为备选中转站j的最大扩散方向与x轴之间的夹角；Wjm为容量等级为m的备选中转站j的处理能力（t）；Wk为垃圾处理厂k的日平均处理能力（t/d）；Pi为居民区i的人口数（人）；Ri为备选中转站对居民区i所产生的环境负效应。

3）决策变量：

1.2.3 数学模型

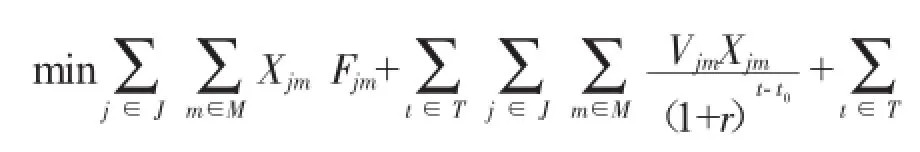
本模型是一个多目标整数规划模型，目标函数（1）为最小化规划使用年限内的费用现值，包括建设中转站的固定投资费用、运营费用，以及各级处理设施之间的垃圾运输费用，通过贴现率进行转换（每年以365 d计）。目标函数（2）为最小化所有居民点所承受的环境总风险。公式（3） 确保每个垃圾收集点的垃圾只被运至1个中转站。公式（4）确保每个中转站的垃圾只被运至1个处理厂。公式（5）表示只有开放的中转站才能接受从垃圾收集点运来的垃圾。公式（6）表示1个中转站备选点只能建立1个某种容量等级的中转站。公式（7）表示中转站处理能力限制。公式（8）表示处理厂处理能力限制。公式（9） 定义了负效应度量Ri。公式（10）约束了各决策变量的取值范围。

2 基于遗传算法的多目标中转站选址问题的求解

2.1 中转站选址问题的遗传算法设计

2.1.1 基因编码

本研究采用基于序数的实数对染色体进行编码。对各垃圾收集点、备选中转站及所有的垃圾处理厂进行实数编号，根据解的特点来确定其染色体的构成：决策变量 Xjm的编码矩阵为 TMT= [1，2，…，M]，对应基因段gene_v=Xjm·TM是J×1整数向量。决策变量Yjk的编码矩阵为TMT=[1，2，…，K]，对应基因段gene_w=Yjk·TK是J×1正整数向量。决策变量Zij的编码矩阵为TJT=[1，2，…，J]，对应基因段gene_u=Zij·TJ是J×1正整数向量。

2.1.2 约束条件处理和适应度值分配

在中转站选址问题中，引入罚函数来处理约束条件，罚函数的构造方法是：

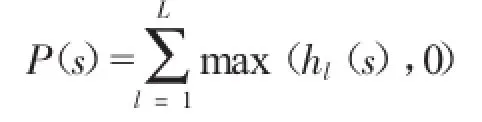
其中：hl（s）为约束函数，L为约束条件总数。

罚函数为：

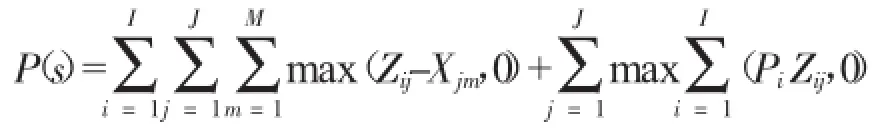
则构造如下的函数：

g1（s）=f1（s）+pn1P（s）

g2（s）=f2（s）+pn2P（s）

其中：pn1、pn2为惩罚项系数，它们随着进化代数的增加而逐渐增加，根据每个个体的函数值用适应度值函数计算他们的适应度值F。

2.1.3 选择操作

本算法中使用轮盘赌机制来进行遗传父代的选择。首先计算个体的适应度总和S=SUM（f1，f2，…，fm）；然后计算各样本的相对概率集R={R1，R2，…，Rm}，其中Ri=fi/S；最后将R进行累加，并随机获取1个0～1的实数r，使得r小于累加的R，输出被选中的个体。

2.1.4 杂交和变异

研究采用的杂交方法是两点均匀杂交，杂交概率设置为Pc=0.9，2个不同的杂交父代，杂交后随机产生2个不同的杂交点，如：

父代一868104828|425672555544|876776673

父代二113102272|776656556549|947776662

随机产生介于0和1之间的1个数ε，如果ε∈[0，1/3]，则2个父代在第1个杂交点之前的部分相互交换第1段；如果ε∈（1/3，2/3]，则在两点之间的部分交换第 2部分；如果 ε∈（2/3，1]，则交换第3部分。例如当ε=1/2时，可以得到2个新的后代：

后代一7868104828776656556549876776673

后代二3811310227242567255554494777666

研究的变异率设定为Pm=0.001，根据变异概率选择某个个体染色体，并将其中的一个基因位取为相反的数字。

2.1.5 算法流程

Step 1：初始化相关参数，给定整个种群规模N、归档集规模M、最大迭代次数Gmax、杂交概率Pc及变异概率Pm；

Step 2：设置当前算法迭代次数Gc=0，随机产生初始种群p0，设置全局最优适应度值fbest（C）=0，最优适应度个体Cbest=C0；

Step 3：设置当前算法迭代次数Gc=Gc+1，通过适应度函数算出种群中个体适应度值；

Step 4：根据上一步计算的个体适应度值，使用适应度值大优先的轮盘赌方法选择个体来作为遗传父代；

Step 5：对于被选中的个体，根据交叉概率及变异概率进行交叉变异操作，产生新的种群；

Step 6：计算新种群中个体适应度值，选择适应度值最高的个体c，将其与全局最优适应度值fbest（C）进行比较，若其适应度值优于全局最优适应度值，则更新全局最优适应度值fbest（C）=fbest（C'），并记录适应度值最高的个体fbest（C）=C'；

Step 7：判断当前迭代次数是否满足要求，若不满足，执行第3步，否则执行下一步；

Step 8：根据记录的最优适应度值的个体Cbest，将其解码为所求问题的全局最优解，并输出结果。

2.2 仿真数据分析

青浦区现有8个镇和3个街道办事处，辖内184个行政村。以青浦城区为分界线（如图1所示），可以将青浦区村镇分为北部片区和南部片区。截止2015年，青浦区共有垃圾收集点1 371个，其中青浦城区有垃圾收集点332个，北部片区村镇垃圾收集点583个，南部片区村镇垃圾收集点456个。青浦区现有垃圾中转站6个，垃圾处理厂1个。

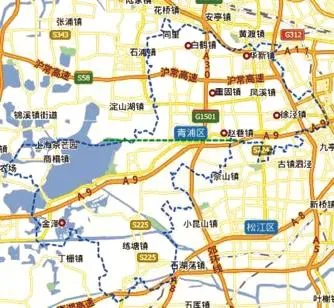
图1 上海市青浦区垃圾中转站分布

由图1可以看出，对于南部片区的村镇，现只有1个垃圾中转站，然而南部片区的垃圾产生量却占总垃圾量的32.28%，由于现有中转站的能力也已经不能满足转运的需求，需要再新建中转站以保证生活垃圾及时得到清运。现假定3个中转站备选点，新建中转站的建设周期为t0=3 a，贴现率r=0.4%，中转站使用年限T=18 a。

为便于计算，将南部片区的相邻4个收集点的垃圾量作为1个收集点的垃圾量，整理后的各垃圾收集点的垃圾量如表1所示。

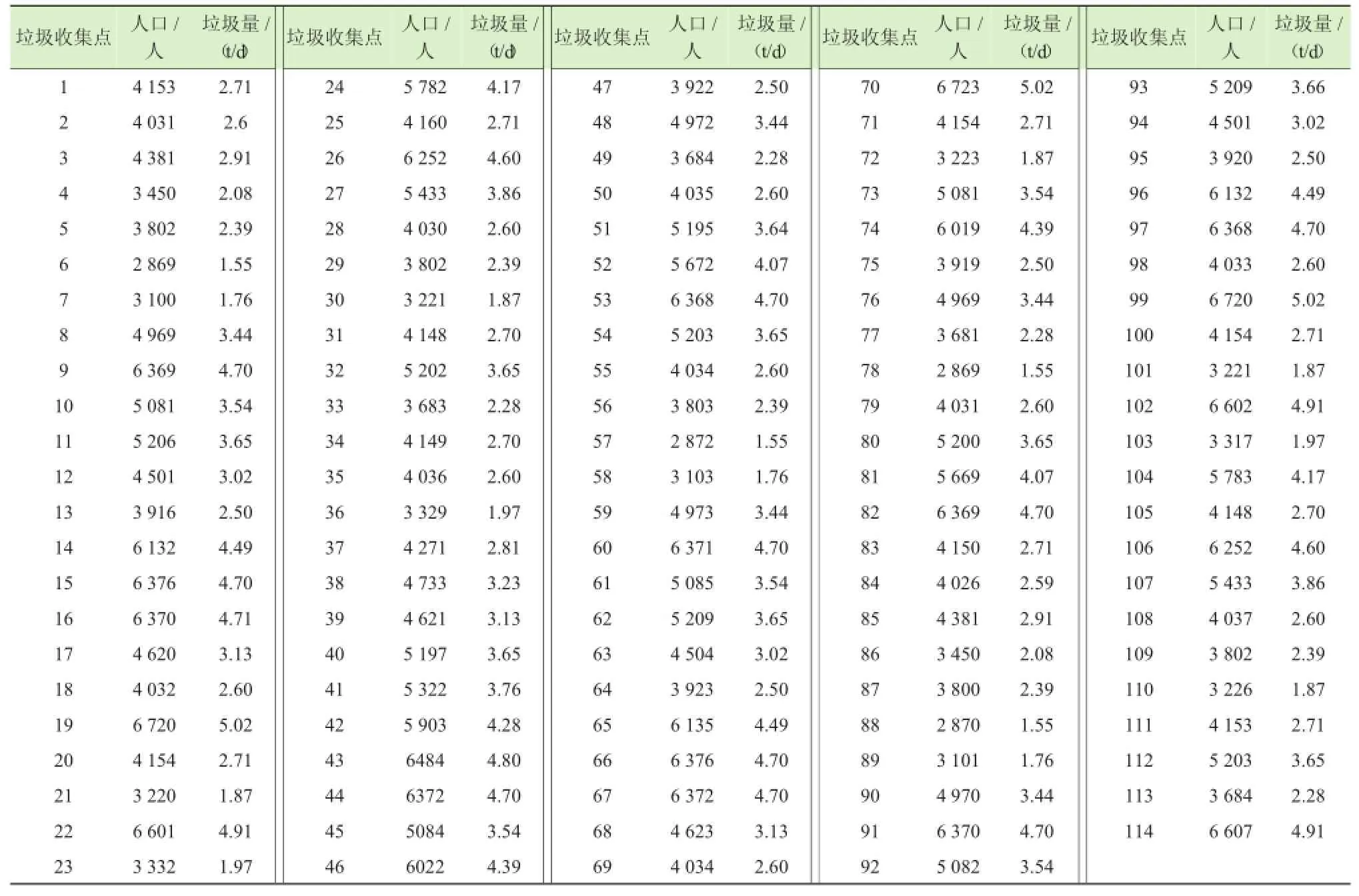
表1 垃圾收集点人口数及日产垃圾量

采用matlab2015a编写模型求解程序，各参数设置如下：种群规模N=80，杂交概率Pc=0.9，变异概率 Pm=0.001，进化代数为 220代，耗时31.211 8 s，最后求得相对最优解如表2所示。

表2 中转站选址优化结果

由上述结果可以看出，应在青浦区南部片区村镇新建1个容量等级为1级的垃圾中转站，以保证南部片区村镇的垃圾能够及时被清运处理。

3 结论

针对村镇生活垃圾中转站选址问题，以成本最小、环境负效应最小为目标函数建立了生活垃圾中转站选址的多目标规划模型，并以上海市青浦区部分村镇为例，基于遗传算法通用性强、容易实现等特点，选择遗传算法进行求解，实验数据也很好地验证了问题求解的有效性，为村镇之后的收运系统规划提供了一定的理论借鉴。

［1］黎磊.村镇生活垃圾收运系统研究［D］.武汉：华中科技大学，2009.

［2］邱江，吴文庆，成效良，等.城市生活垃圾转运站的建设［J］.环境卫生工程，2003，11（3）：159-161.

［3］贾传兴，彭旭亚，刘国涛，等.城市垃圾中转站选址优化模型的建立及其应用［J］.环境科学学报，2006，26（11）：1927-1931.

［4］李萍.西安市三民村生活垃圾中转站的建设［J］.环境卫生工程，2007，15（1）：57-59.

［5］Erkut E，Neuman S.A multiobjective model for locating undesirable facilities［J］.Ann Operat Res，1993，40：275-291.

［6］Melachrinoudis E，Min H，Wu X.A multiobjective model for the dynamic location of landfills［J］.Location Sci，1995，3（3）：143-166.

Site Selection Optimization of Rural Domestic Waste Transfer Station

Li Qianqian1，Ma Huimin2，Chen Yijun1，Bi Zhujie3
（1.Shanghai City Appearance and Environmental Quality Monitoring Center，Shanghai 200085；2.Business School，Shanghai Dianji University，Shanghai 201306；3.Shanghai Institute for Design&Research on Environmental Engineering Co.Ltd.，Shanghai200232）

In view of the problem of the site selection of rural domestic waste transfer station，the total cost of the waste collection system，the number and scale of the establishment of the transfer station，the service area of the transfer station，and the negative effect of the environment in the residential area were considered.With the minimum cost and environmental negative effect as the objective function，a multi-objective programming model was established.Taking part of villages in Shanghai Qingpu district asan example，we used genetic algorithm to solve the problem.

rural domestic waste；site selection；genetic algorithm

X705

A

1005-8206（2017）01-0066-04

李倩茜（1990—），主要从事物流系统规划理论与方法。

国家科技支撑计划课题《村镇生活垃圾城镇一体化处理与资源化利用技术及工程示范研究》（2014BAL02B03）

2016-07-29