基于矢量谐振控制的负荷补偿装置研究

王祺，杨宇，韩肖清

（1.太原理工大学电力系统运行与控制山西省重点实验室，山西太原030024；2.国网山西省电力公司，山西太原030001）

基于矢量谐振控制的负荷补偿装置研究

王祺1，杨宇2，韩肖清1

（1.太原理工大学电力系统运行与控制山西省重点实验室，山西太原030024；2.国网山西省电力公司，山西太原030001）

通过对某地区居民、工业两类典型负荷数据的采集，利用电压不平衡和电压偏差两项指标分析了该地区在不同时间段内的负荷数据。针对分析结果所体现的电能质量问题，提出了一种基于矢量谐振控制的三相四线制有源电力滤波器控制策略，同时对比分析了矢量谐振控制器与传统比例谐振控制器的幅频特性和相频特性，仿真结果表明，所提的矢量控制器能在较大范围内保持较高的增益，有良好的频率选择性和较大的稳定裕度。最后，采用提出的控制策略完成了一台实验样机，经现场实测验证了该策略的可行性，电能质量有所改善，实验结果达到预期效果。

电能质量；矢量谐振控制器；比例谐振控制器；三相四线制APF

0 引言

随着现代科学技术的发展，造成电能质量问题的因素越来越多，非线性负载、三相负荷的不平衡等因素对电能质量有一定影响。非线性负载使电网谐波含量增多，三相负荷不平衡会使电压不平衡度、电压偏差增大，进而影响电能质量[1-2]。

传统改善电能质量的方法有局部并联电容器组、无源滤波器等。局部并联电容器组可补偿系统无功功率，解决电压偏低的情况，但无法解决轻载电压偏高的电能质量问题；无源滤波器通过电感电容谐振(LC谐振)改善谐波电流，但只能抑制某固定频率谐波，同时可能造成系统谐振[3-5]。

1 电压质量分析

三相电压不平衡是指在电力系统中各相之间电压不相等或相角不相等，且幅值差超过规定范围。电网正常运行时，负序电压不平衡度不超过2%，短时不得超过4%；电压偏差指的是供电系统在正常运行方式下，某一节点的实际电压与系统额定电压之差对系统额定电压的百分数，20 kV及以下三相供电电压偏差为标称电压的±7%，220 V单相供电电压偏差为标称电压的＋7%、－10%。

1.1 数据采集

选取山西某电网内居民、工业两类典型负荷作为数据采集点。采集时间为2013年10月至2014年9月总计12个月，每月选择11日至15日共5 d，总计60 d。每天24 h中，每间隔5 min采集数据1次，每小时采集12点。

电压偏差数学表达式为

式中，δV为电压偏差；V为实际电压，kV；VN为系统额定电压，kV。

相电压计算三相电压不平衡度计算公式为

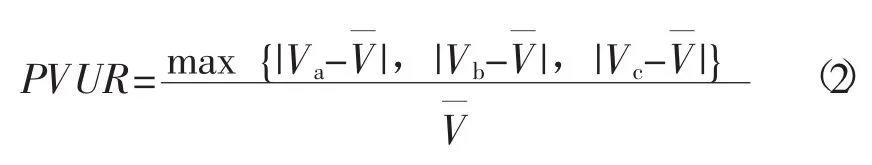
式中，Va、Vb、Vc为相电压有效值，V¯为三相相电压平均值。

1.2 数据处理及分析

1.2.1 居民负荷

以10 kV科海开闭所变电站10 kV母线Ⅰ751断路器（科海Ⅰ回）为居民负荷数据采集点。采集的数据类型为10 kV配电网末端的A、B、C三相的相电压，AB、BC、CA两相间的线电压。

1.2.1.1 三相电压不平衡

根据公式（2），计算得出每个采集时刻的220 V侧的A、B、C三相电压的不平衡度，取平均值，作为该点三相电压不平衡度的代表。以日期为横坐标，电压不平衡度为纵坐标，作出三相电压不平衡度的折线图如图1所示。

图1 220 V相电压不平衡度平均值折线图

根据220 V侧的三相电压不平衡度的折线图可知，不平衡度的平均值在0.25%到0.45%之间波动。观察220 V相电压不平衡度平均值折线图，有一点不平衡度高达1.87%，对应日期为2014年2月13日，农历正月十五元宵节，不难理解过大的用电负荷导致三相电压不平衡度的增高。

1.2.1.2 电压偏差

根据公式(1)，并由采集到的点分析出，A相电压为三相电压的中间值，故选取每个采集点的10 kV侧的A相电压和220 V侧的A相电压值，计算电压偏差，其中10 kV侧的额定电压UN=10/≈5.774 kV，220 V侧的额定电压UN=220 V。以天为单位，选取平均值，作为该点电压偏差的代表，做出A相电压偏差的折线图如图2所示。

图2 220 V侧A相电压偏差平均值折线图

根据220 V侧的A相电压偏差的折线图可知，平均值在2.5%到5%之间波动。全年A相电压偏差最大值出现在2014年1月15日，电压偏差最小值出现在2014年7月14日，当天对应的电压偏差平均值分别为4.60%和2.80%。

1.2.2 工业负荷

以110 kV维尼纶变电站10 kV母线Ⅰ586断路器（一高配）为工业负荷数据采集点，采集的数据类型为10 kV配电网末端的A、B、C三相的相电压。

1.2.2.1 三相电压不平衡

根据公式（3），计算得出采集点每个采集时刻的10 kV侧的A、B、C三相电压不平衡度，以天为单位，取平均值，作为该点三相电压不平衡度的代表。以日期为横坐标，电压不平衡度为纵坐标，做出三相电压不平衡度的折线图如图3所示。

图3 三相电压不平衡度平均值折线图

根据三相电压不平衡度的折线图可知，平均值在0.2%到1.4%之间波动。三相电压不平衡度较大值出现在4月份到6月份，较小值出现在10月份到12月份，其余月份较为平稳，说明了该工厂在第三季度生产量较高，第一季度生产量较低，第二季度和第四季度生产平稳。

1.2.2.2 电压偏差

根据公式(1)，仍选取采集点每个时刻的A相电压值，计算得到电压偏差，其中额定电压≈5.774 kV。以天为单位，取平均值，作为该点电压偏差的代表。以日期为横坐标，电压偏差为纵坐标，做出A相电压偏差的折线图如图4所示。

图4 A相电压偏差平均值折线图

根据A相电压偏差的折线图可知，平均值在3%到6%之间波动。全年A相电压偏差最大值出现在2014年6月14日，电压偏差最小值出现在2013年11月14日，当天对应的电压偏差平均值分别为5.99%和3.99%。

2 控制策略

2.1 三相四线制APF的结构及小信号模型

2.1.1 主电路拓扑结构

图5所示为电容中点型三相四线制有源电力滤波器APF（active power filter）的主电路结构图，APF可以等效为电压源型逆变器。为了抑制配电系统的零序电流，从APF直流侧分裂电容中点引出中性线构成回路，对零序电流进行补偿。

图5 三相四线制APF主电路结构图

其中，ism、ifm、ilm、em、vm(m=a，b，c)分别为三相电网电流、APF输入补偿电流、负荷电流、三相电网电压、逆变器出口电压，vdc1、vdc2分别表示直流侧电容C1、C2上的电压，L为三相四线制APF的连接电抗器，R为考虑连接电抗器内阻、开关器件损耗、逆变器死区效应的等效电阻。

2.1.2 小信号模型

传统的APF数学模型，通常选取APF的补偿电流为状态变量，本文直接以电网电流ism为控制目标、直流母线电压vdc为状态变量，负荷电流ilm为扰动变量，建立公式（3）所示的三相四线制APF的交流小信号模型。

稳态运行中，直流电压vdc波动性小，惯性大，忽略直流侧电压中含dd、dq、d0项，对公式（3）进行拉普拉斯变换，可得公式（4）。

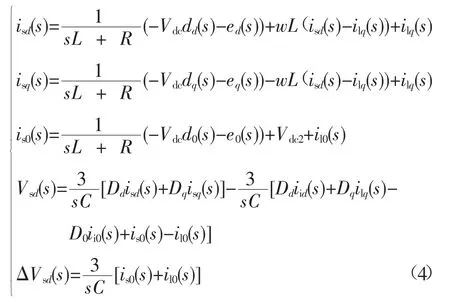
结合两式可得如图6所示的三相四线制APF的简化电流环，此时，被控对象的传递函数可近似为一阶惯性环节，影响系统的相位响应。解耦后的d轴电流环控制结构如图6a所示，简化、合并后的d轴电流环控制结构如图6b所示。

根据上述分析，vd*、vq*、v0*的控制方程可以表示为

其中，Gc(s)、Gc0(s)分别表示相应的电流控制器。

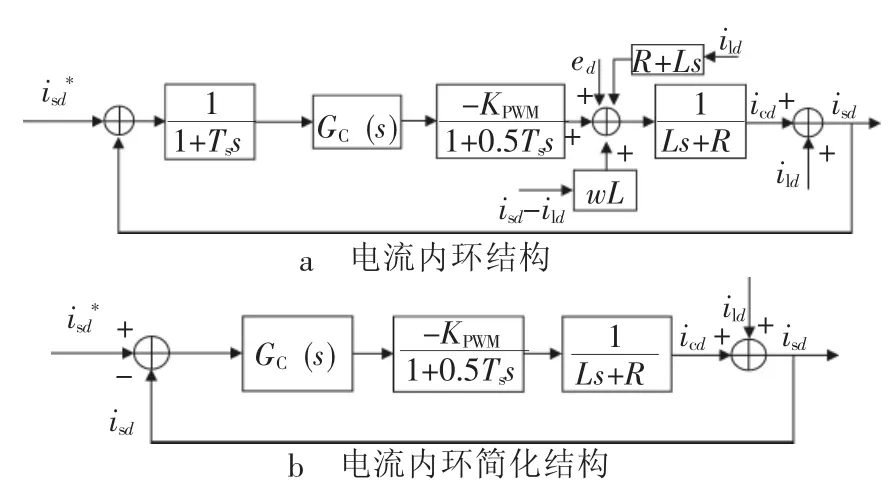
图6 系统电流环控制图

2.2 矢量谐振控制VRC

公式(6)、(7)分别为比例谐振控制PRC (proportional resonant controller）、矢量谐振控制器VRC（vector resonance controller）的传递函数。

其中，KPR、KVR分别为比例谐振控制PRC、矢量谐振控制VRC的增益系数，Kp代表比例谐振控制PRC、矢量谐振控制VRC的比例系数，nω0为对应的谐振频率点，ωc为拓展带宽引入的阻尼因子，R、L分别为被控对象的等效电阻、电感。如图7所示，为公式(6)、(7)的bode图。

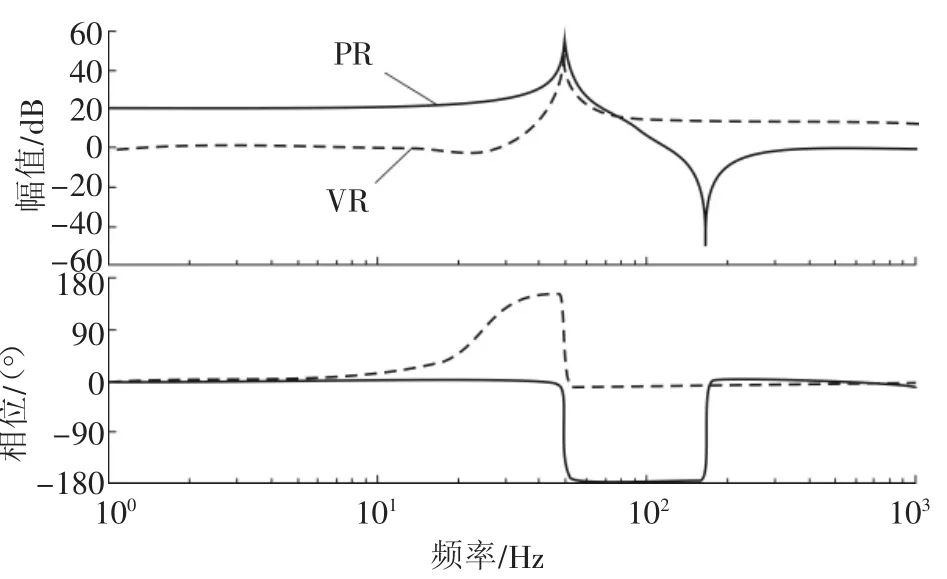
图7 比例谐振控制PRC、矢量谐振控制VRC的bode图

从PRC、VRC性能比较图中可以看出，在谐振点处，PRC、VRC均可获得较大增益，VRC谐振过后增益平稳，PRC谐振过后增益先减小后趋于平稳，两者均可快速跟踪、控制交流信号，有良好的选择性。由相频特性可知，PRC在谐振点处，相位滞后近90°，而VRC在谐振点处的相位保持稳定。可见采用VRC控制时，并不影响系统的相位，有较好的稳定性和相位裕度。

2.3 电流控制器的性能分析

在旋转坐标系下，d、q轴电流内环具有对称性，以d轴电流id控制为例，进行电流控制器Gc(s)的设计；电网电流的0轴谐波含量与d、q轴不同，因此，0轴电流控制器Gc0(s)需要参考d轴的电流控制器Gc(s)进行单独设计[6-7]。

首先忽略采样及脉宽调制PWM(pulse width modulation)环节延时影响，电流控制器分别采用PRC、VRC时，三相四线制APF控制系统的开环传递函数如公式（8）、（9）所示。

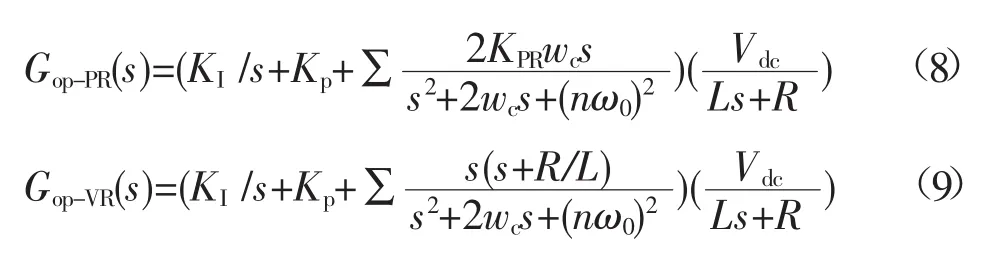
如图8a所示，对PRC、VRC的开环特性进行比较，其中基频ω0=100π，R约等于0.1Ω，L=1 mH，KP=1，KPR=1 000，KVR=5，阻尼因子ωc=5n，取nmax=10为例进行分析。由图的幅频特性可见，两者在谐振频率点出获得较大增益。由相频特性可见，在谐振点处PRC相位滞后90°～ 180°，VRC相位几乎无滞后，说明VRC的相位稳定裕度更高。在闭环比较图（图8b）中，两者相频特性在谐振点处增益接近于0，PRC闭环系统在谐振频率点附近产生非期望高频增益，恶化了APF的补偿性能，VRC则在较大范围内保持了较高的增益，使得APF具有较好的补偿性能和稳定裕度[8]。

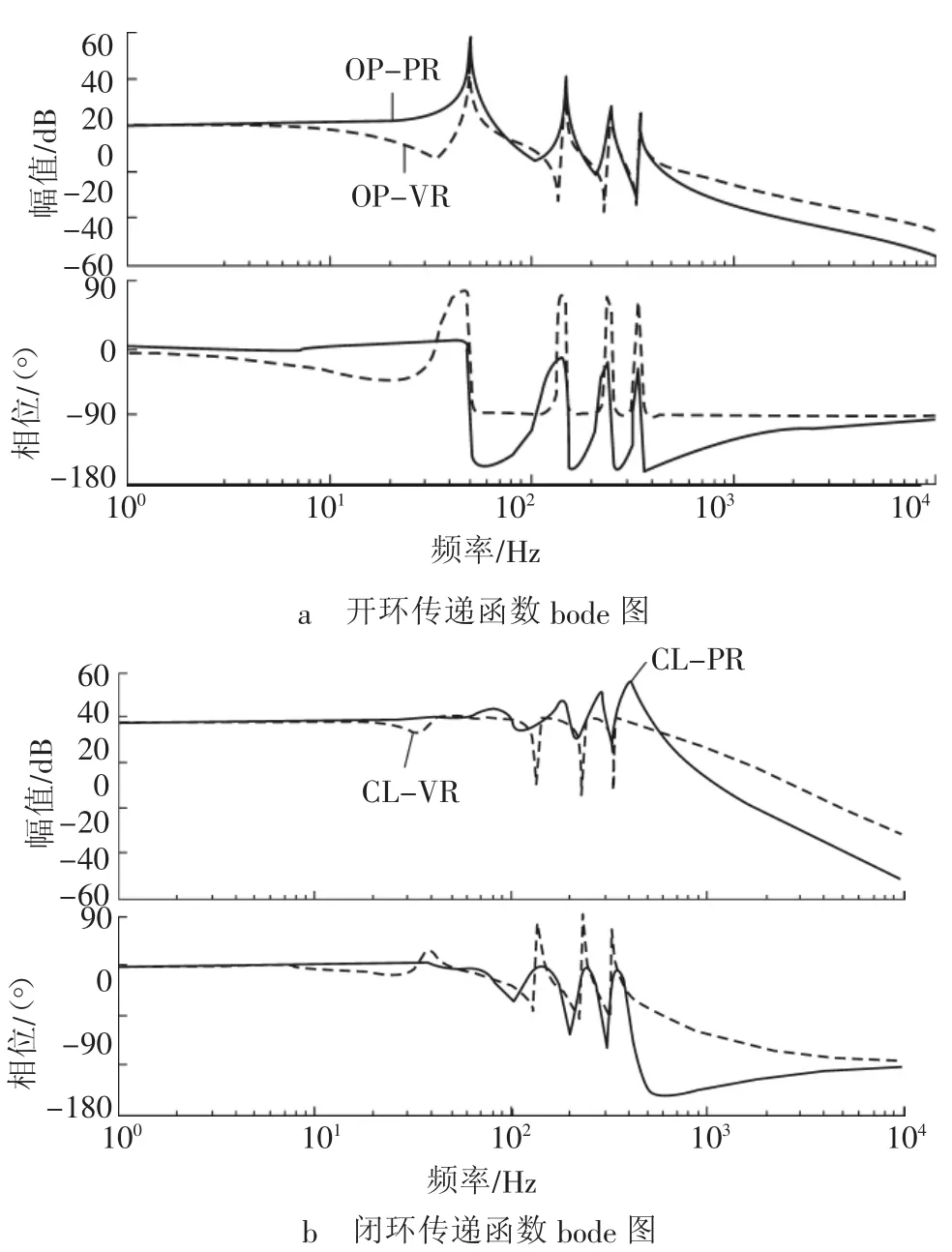
图8 控制系统的bode图

综上，VRC相比于PRC具有更好的选择性，有较高的稳定裕度，故选用矢量谐振控制VRC作为电流环的主控制器。

2.4 仿真与实验结果

为进一步验证上述控制方案的有效性与正确性，在上述分析的基础上，分别进行仿真与样机实验验证。表1所示为三相四线制APF的相关仿真实验参数。

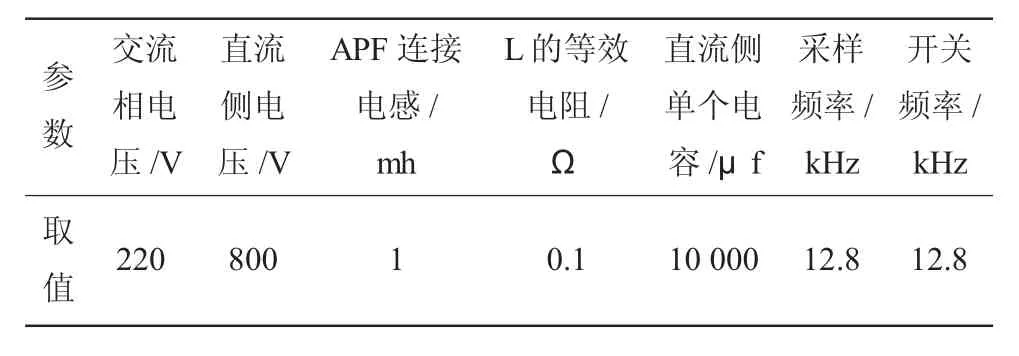
表1 APF仿真实验参数

如图9、10所示，为模拟某一时刻某高校实验楼0.4 kV配电系统APF投入前后电网电流、负荷电流、补偿电流及各自对应的傅里叶FFT（fast Fourier transform）分析结果。APF在0.08 s投入运行，同时负荷在0.3 s时发生突变，对负荷电流及补偿后电网电流进行FFT分析。APF未投入时，负荷谐波畸变为42.68%、37.22%、26.76%，幅值为169.4、119.7、247.5，电能质量不符合相关标准，严重影响电网的安全稳定运行，需加入APF进行补偿。加入矢量谐振控制VRC三相四线制APF补偿后，考虑负荷突变，电网侧电流波形的畸变率从61.12%、59.60%、25.83%变为8.54%、7.67%、7.2%，幅值从79.49、156.1、191.5变为88.53、92.17、91.76，对电网的不平衡度、谐波等有良好抑制作用，电能质量有所改善。

在上述分析、验证的基础上，开发了实验样机，并进行实测。实验样机除实现APF补偿功能外，还具有电能质量检测、通讯等功能，综合考虑核心处理器选用TI公司的32位双核DSPTMS320F28377D作为主件，采用合利时的人机界面作为上位机，通过modebus总线与DSP进行通讯。功率模块采用英飞凌公司的FF150R12RT4作为主电路开关器件，直流侧电容选取2个10 000μf/450 V电解电容串联，APF连接电抗器选取为1 mh/50 A，实验参数与仿真参数一致。

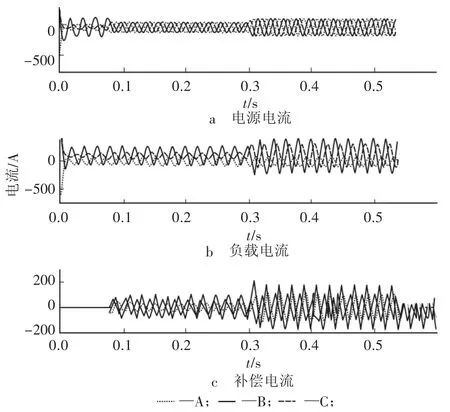
图9 APF投入前后的电流波形

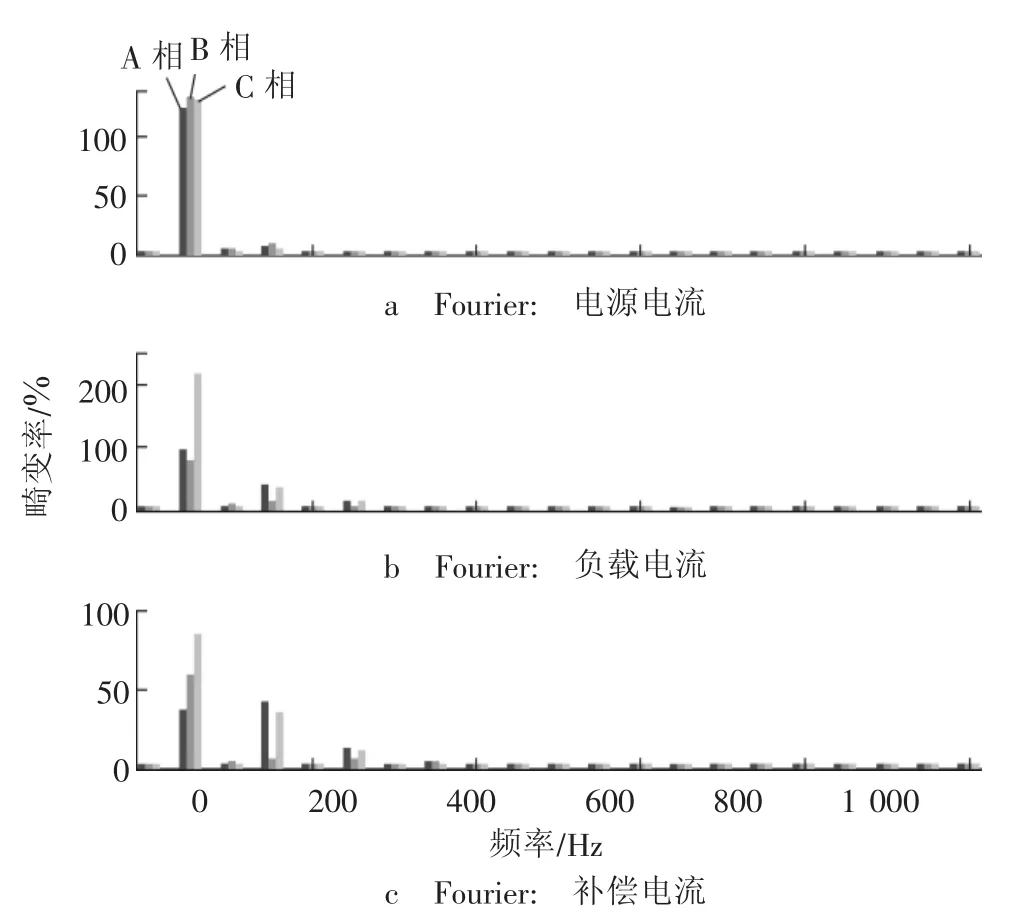
图10 电流FFT分析

图11 APF治理后的电流波形和FFT分析

图11 a、c所示为实验楼实测负荷电流波形及FFT分析结果，畸变率分别为：20.45%、17.3%、27.95%。图11b、d为采用delta变换的改进型矢量谐振控制VRC的三相四线制APF补偿后[9]，电网电流的控制效果及傅里叶(FFT)分析结果，电流畸变率降为6.09%、5.79%、3.44%，基本满足国家标准。

4 总结

本文通过对某地区居民、工业两类典型负荷数据的采集，利用电压不平衡和电压偏差分析了该地区在不同时间段内的负荷数据，针对分析结果所体现的电能质量问题，制定了一种基于矢量谐振控制的三相四线制APF控制策略，并采用此策略开发了一台实验样机，经现场实测验证了该策略的可行性，电能质量有所改善，实验结果达到预期效果。本文所提出的控制策略将对工程中三相四线制APF的设计有指导意义。

[1]赵莉华，雷晶晶，荣强．民用负荷对配电网电能质量的影响[J]．电测与仪表，2015，52(08)：50-55.

[2]陈允平，王旭蕊，常青，等．电力系统三相非线性元件的谐波序网等效研究[J]．中国电机工程学报，2001，21(4)：31-35.

[3]Buso S,Malesani L,Mattavelli P.Comparison of current control techniques for active filter applications[J].IEEE Transactions on Industrial Electronics,1998,45(5):722-729.

[4]Lascu C,Asiminoaei L,Boldea I,et al.High Performance Current Controller for Selective Harmonic Compensation in Active Power Filters[J].IEEE Transactions on Power Electronics.2007,22(5):1826-1835.

[5]Lascu C,Asiminoaei L,Boldea I,et al.Frequency Response Analysis of Current Controllers for Selective Harmonic Compensation in Active Power Filters[J].IEEE Transactions on Industrial Electronics.2009,56(2):337-347.

[6]张树全，戴珂，谢斌，等．多同步旋转坐标系下指定次谐波电流控制[J]．中国电机工程学报，2010，30(3)：55-62.

[7]宋亦鹏，年珩.谐波电网电压下基于矢量谐振控制的双馈异步发电机集成控制策略[J]．电工技术学报，2014，29(7)：187-199.

[8]Yepes A G,Freijedo F D,Doval-Gandoy J,et al.Effects of Discretization Methods on the Performance of Resonant Controllers[J].IEEE Transactions on Power Electronics.2010, 25(7):1692-1712.

[9]Kanaan H Y,Hayek A,Georges S,Al-Haddad K,et al.Averaged Modeling,Simulation and Linear Control Design of a PWM Fixed Frequency Three-Phase Four-Wire Shunt Active Power Filter for a Typical Industrial Load[J].The 3rdIET International Conference on Power Electronics,Machines and Drives,2006：252-256．

Research of Load Compensator Based on Vector Resonance Control

WANG Qi1,YANG Yu2,HAN Xiaoqing1
（1.Shanxi Key Lab of PSOC,Taiyuan University of Technology,Taiyuan,Shanxi 030024,China；2.State Grid Shanxi Electric Power Corporation,Taiyuan,Shanxi 030001,China）

The residential and industrial load data were collected from a region,and the load data during different period are analyzed by referring voltage deviation and voltage unbalance degree.According to the power quality problem reflected from the results of the analysis above,this article puts forward a vector-resonance-control-based control strategy for three-phase four-wire APF.Meanwhile,the amplitude-frequency characteristic and phase frequency characteristics of vector resonance controller and proportional resonant controller were compared.The simulation results showed that the proposed vector controller can keep high gain on a wider range and better frequency selectivity and stability margin.Finally,an experimental prototype was made through the proposed control strategy.Through field test,the feasibility of the strategy was verified and power quality was then improved,so that the experimental results had achieved the desired effect.

power quality;vector resonance controller；proportional resonant controller；three-phase four-wire APF

TM761

A

1671-0320（2017）01-0058-06

2016-10-11，

2016-11-29

王祺（1991），男，山西山阴人，2015级太原理工大学电气工程及其自动化专业硕士在读，研究方向为新能源发电、微电网的运行与控制；杨宇（1975），男，山西运城人，2007年毕业于西安交通大学电气工程及其自动化专业，博士，研究方向为电力系统的运行与控制、电力电子在电力系统的应用；韩肖清（1964），女，山西太原人，1985年毕业于太原工业大学电力系统专业，教授，博士生导师，研究方向为电力系统运行与控制、新能源与微电网运行。