基于超快多维振动光谱技术解析分子体系的三维空间构型

2017-03-13陈海龙边红涛郑俊荣

物理化学学报 2017年1期

陈海龙边红涛郑俊荣

(1北京大学化学与分子工程学院，北京分子科学国家实验室，北京100871；2中国科学院物理研究所，北京凝聚态物理国家实验室和中科院软物质物理重点实验室，北京100190；3陕西师范大学化学化工学院，西安710119)

陈海龙2边红涛3郑俊荣1,*

超快多维振动光谱技术目前已经被广泛应用到各种凝聚态分子体系中分子的结构以及快速变化动力学过程的测量之中，并有望成为新一代解析分子体系微观结构及超快行为的常规手段。本文从两个主线出发，介绍如何利用超快多维振动光谱技术解析分子体系的三维空间构型。一方面通过测量分子内各个振动模式跃迁偶极矩间的夹角来获得分子体系内不同基团的相对空间取向，并最终确定分子的空间构型。另一方面，通过详细解析分子间振动能量转移的机理，进而将实验中测得的振动能量转移速率转化为分子之间的距离信息。

多维振动光谱仪；超快光谱；二维红外光谱；分子构象；振动能量传递

1 引言

超快多维振动光谱技术是通过多束波长在中红外的超短脉冲激光(通常是从几十个飞秒到几个皮秒)对分子各个化学键的振动模式进行顺序激发，从而获得关于分子动态及静态结构信息的方法。这种方法可以在飞秒到皮秒的时间尺度上检测分子体系中原子核的振动行为，并可以得到分子内以及分子间不同振动模式的相互关联。因此，与原子核运动相关的各种分子体系微观结构信息以及快速变化动力学过程，例如化学键或氢键的形成及断裂，分子或化学键的转动，振动能量的传递等，都可通过这一技术来进行研究1－29。目前这一方法已经被广泛应用于化学反应机理1－3，水及水溶液微观结构和动力学过程30－36，蛋白质、多肽动力学及结构19－21,37－46，氢键动力学及热动力学25,26,47－50，分子振动耦合及能量弛豫51－55，电荷转移56,57，等等各类分子体系中重要科学问题的研究。

陈海龙，1984年生。2002年本科毕业于北京大学物理学院物理学系，2011年博士毕业于中国科学院物理研究所光学专业。2011－2016年在美国莱斯大学化学系从事博士后研究。现为中国科学院物理研究所软物质物理重点实验室副研究员。主要研究方向为各类先进超快激光光谱技术的发展以及应用，分子体系微观结构及分子间能量传递过程的测量，二维材料及各类光电材料中超快光电转换过程机理的研究。主持国家自然科学基金1项。

边红涛，1982年生。2003年本科毕业于西安交通大学理学院应用化学系，2009年博士毕业于中国科学院化学研究所物理化学专业。随后在美国莱斯大学和埃默里大学从事博士后研究。2016年加入陕西师范大学化学化工学院。主要从事超快激光光谱新技术应用和新方法的建立，在分子层次上开展各种凝聚相体系和各种界面/表面的分子构象和取向结构、分子间能量传递物理化学过程等方面的研究。参与国家自然科学基金3项。

郑俊荣，1973年生。1997年本科毕业于北京大学化学系，2000年北京大学高分子化学硕士。2003年美国伦塞勒理工高分子物理硕士。2007年美国斯坦福大学物理化学博士。2008－2009年分别在美国斯坦福大学和加州大学伯克利分校从事博士后和访问学者研究。2009－2015年在美国莱斯大学化学系任教。2015年加入北京大学化学与分子工程学院。主要研究方向为各类先进超快激光光谱技术和二次电池的开发、应用及商品化。美国斯隆奖和帕卡德奖获得者。主持美国及中国自然科学基金、美国空军及美国化学会等组织科研项目13项。

近几年来，原美国莱斯大学(Rice University)郑俊荣教授课题组一直致力于将超快多维振动光谱技术发展成为解析分子体系三维空间构型的常规手段58－75。在凝聚态分子体系中，分子构型的快速变化对于很多重要的化学和生物学过程有着非常重要的意义，例如化学反应的选择性、蛋白质折叠、生物膜融合、以及分子识别等76－82。目前，人们已经发展出多种技术手段以用于分子空间构型的解析。其中，X射线衍射(XRD)方法以及核磁共振(NMR)方法是目前最为常用的，同时也是非常有效的分子结构测量手段。但是这些方法自身的一些特点限制了它们的适用范围，例如NMR方法的时间分辨率较低，通常只能达到微秒的量级，因此也就无法用来测量一些快速涨落的分子构型以及一些寿命较短的化学反应中间态61,83,84。而XRD方法则通常要求待测体系有一定的空间周期结构，极大地限制了它的应用范围。因此在实际情况中，会有很多分子体系的空间构型无法利用传统的方法进行解析。举例来说，为了研究一些化学反应的分子机理，我们最好能够对这些催化反应中间产物的分子结构进行直接观测。但是由某些酶参与的催化反应的中间产物通常具有顺磁性以及较短的寿命，甚至有时很难溶解，这些特点都限制了传统的NMR方法对其结构进行解析。此外，这些分子往往都很难制备成单晶，因此也限制了XRD方法的应用。即便有时可以结成晶体，也大都非常脆弱，容易被高强度的X射线所损伤。电子顺磁共振(EPR)也被广泛应用到这些分子体系中电子自旋的探测，并从中得到许多重要的分子信息，但是EPR方法也无法用来直接解析分子的三维空间结构。同样的问题也存在于对其它各类有机化学分子或生物体系中含金属分子结构的测量。由于无法对化学反应中间产物的分子结构进行直接观测，因此也很难从实验上直接证实人们所假设的各种反应途径，使得很多化学和生物催化机理一直都无法得到很好的解答。

而多维振动光谱技术，经过过去几年我们的研究，现在可以比较定量地通过测量分子内各个振动模式跃迁偶极矩间的夹角来获得分子体系内不同基团的相对空间取向，以及通过振动能量转移过程测量分子之间的距离。其时间分辨率可以达到飞秒的量级，并可以适用于几乎所有的凝聚态体系，从而有着更为广泛的适用范围，并有希望成为新一代解析分子体系三维空间构型的有力手段。在本篇综述中，将首先简要介绍超快多维振动光谱技术的实验装置与原理，之后通过两个主线详细介绍我们相关的一些工作：(1)如何通过测量分子内各个振动模式跃迁偶极矩间的相对取向来获得分子体系的三维空间结构信息；(2)如何测量分子间的振动能量传递过程，并将实验中测得的传能速率转化为分子之间的距离。

2 实验装置简述

分子体系中振动模式之间的夹角以及振动能量传递过程都可以通过超快多维振动光谱仪来测量。传统的多维振动光谱技术，即二维红外方法，在实验上有多种手段可以实现7－10,61,85－89。而近几年来，我们通过对传统的二维红外技术进行的一系列改进，逐步发展了一种独特的“窄带高能量激发-超宽谱带探测”的超快多维振动光谱测量手段，并拥有传统方法所无可比拟的诸多优点63－65。

首先，激光光源由传统的一台飞秒激光放大器扩展为一对时间同步的飞秒及皮秒激光放大器。进而将窄带高能量的皮秒激光光源独自作为样品的激发光，以对分子体系中任意的振动模式进行选择性地激发，并因此获得极高的激发效率。而传统的二维红外方法，无论采用的是光子回声(photon echo)技术90,91，还是借助于声光调制器等8,86－89，都只能选取飞秒激光放大器的部分能量作为激发光。并在对激发光的处理过程中，例如通过声光调制器，能量还会进一步损失。更重要的是，由于其激发源采用的是宽谱带的飞秒激光，因此在对分子的激发过程中，分配到单个振动模式上的能量也只是其中的一小部分，进而导致产生的三阶非线性信号较小。因此在实际运用中，传统的二维红外方法通常只能局限于对一些较强的振动吸收峰进行测量，所得到的分子结构信息也非常有限。而利用独立的皮秒激发光的方法，对单个振动模式的激发效率至少要提高一个数量级以上，因此极大地提高了所产生的三阶非线性信号的强度，进而获得大量传统方法所无法测量到的分子振动模式间的相互耦合信息61。其测量范围几乎涵盖了分子体系中所有重要的化学键所参与的振动模式，因此可以获得充足的分子结构及动力学信息，最终解析出分子的三维结构及其动态变化。

另一方面，将传统的由光参量放大器产生的中红外探测光源改为超连续中红外-太赫兹飞秒脉冲光源。通过将高强度的800 nm/400 nm混合飞秒激光脉冲聚焦在空气中将空气电离产生等离子体，可以从中获得同时覆盖整个中红外乃至远红外太赫兹光谱区域的超宽光谱63－65,92,93。而传统中红外探测光源的谱宽通常仅有约100－200个波数，为获得更宽的探测范围，只能通过不断改变中心波长来实现，并且也无法将探测延伸到低频振动模式，如远红外区振动模式的测量。超宽光谱的探测光源，结合可独立调频的窄带高能量的激发光源也使得对多维振动光谱的采集时间极大地缩短。具体在实验中所采用的光路以及超连续探测光源的光谱如图1所示。

具体来说，首先将一个重复频率为76 MHz的飞秒振荡器产生的飞秒脉冲激光分为两个部分，分别作为一对同步的皮秒和飞秒放大器的种子光。皮秒放大器所产生的激光(~1 ps，1 kHz)经由一台光参器放大器产生约0.8 ps的中红外脉冲，其频率在500 cm－1到4000 cm－1之间连续可调，带宽为10－35 cm－1，能量为每个脉冲约1－40 μJ。而飞秒放大器所产生的激光(~40 fs，1 kHz)经由β相偏硼酸钡(BBO)晶体倍频后聚焦在空气中产生一个脉冲宽度小于100 fs，频率范围从小于10 cm－1覆盖到大于3500 cm－1的中红外-太赫兹超连续脉冲光源63,64。在超快多维振动光谱实验中，皮秒红外激光聚焦在样品上用来激发样品，其光斑大小约100－500 μm，能量的大小根据实际需求可进行调节。而飞秒超连续光源作为样品的探测光，透过样品后被光谱仪收集。探测器通常采用碲镉汞(MCT)阵列元件，其光谱分辨率与探测的中心波长有关，约为1－3 cm－1。

图1 超快多维振动光谱实验装置及超连续探测光光谱图64Fig.1 Laser setup of ultrafast multiple-dimensional vibrational spectroscopy and the measured spectra of detection beam64

通过调节光参量放大器以及光谱仪可以分别扫描激发光以及探测光的频率，而通过改变两束光的时间延迟可以得到样品激发态随时间变化的信息。图2所示为一典型的多维振动光谱图69，激发光的频率记为ω1，作为多维振动光谱的x轴；探测光的频率记为ω3，作为多维振动光谱的y轴，时间固定在0.2 ps附近。通过对其中各个信号峰进行分析，便可以获得样品的分子构型信息。

此外，在探测光的路径中还需插入一对偏振片以改变探测光相对于激发光的偏振状态。通常在实验中，需要分别测量在二者偏振平行以及垂直情况下信号强度的大小，分别记为I‖与I⊥，由此得到信号的各向异性信息R(t)=(I‖－I⊥)/(I‖+ 2I⊥)。通常会有两个原因导致R(t)值随时间进行衰减：分子转动与共振能量转移61，其中后者可以用来测量共振能量传递的速率。而在非共振能量转移的测量实验中，用Ilife(t)=I‖+2I⊥来表示各向同性信号的大小，可以排除分子自身转动的影响。

3 分子体系三维空间构型的解析

3.1 4′-甲基-2′-硝基乙酰苯胺(MNA)分子构型的测量

分子体系的三维空间构型，可以利用多维振动光谱技术通过测量分子内各个振动模式跃迁偶极矩间的相对取向来获得62－64,68,69。我们首先选择MNA作为模型分子来测量它在不同环境下的三维空间构型64。通过与XRD结果比较来标定这个新方法的准确度，MNA分子可以在不同的溶液中形成不同的结晶，例如，在饱和水-乙醇混合溶液中会析出白色的晶体，而在其它一些非极性饱和溶液中会析出黄色的晶体，二者分别对应于不同的晶体结构以及分子空间构型94。利用XRD方法，人们已经测量了这两不同晶体的分子结构95，如图3所示。MNA分子的主体构型可由三个分子平面的相对夹角所确定，分别是：(1)苯环所形成的平面；(2)硝基所形成的平面；(3)酰胺所形成的平面。在MNA分子晶体中，硝基上的氢原子既可以与相邻另一个MNA分子氨基上的氧原子结成氢键(白色晶体)，也可以与同一分子内氨基上的氧原子结合成氢键(黄色晶体)，进而形成不同的分子空间构型，对应于三个平面形成不同的夹角，如图3所示。其中，在白色晶体内，MNA分子只有一个空间构型，标记为MNA-W；而在黄色晶体内则有两个，分别标记为MNA-Y1和MNA-Y2。接下来将以MNA分子在不同环境下(白色晶体，黄色晶体，溶液，以及熔融状态)三维构型的解析为例，介绍一下利用多维振动光谱方法测量分子空间构型的基本原理。

图2 氰基乙烯乙酸酯在0.2 ps时刻的多维振动光谱图69Fig.2 Multiple-dimensional vibrational spectrum of 1-cyanovinyl acetate at a waiting time of 0.2 ps69

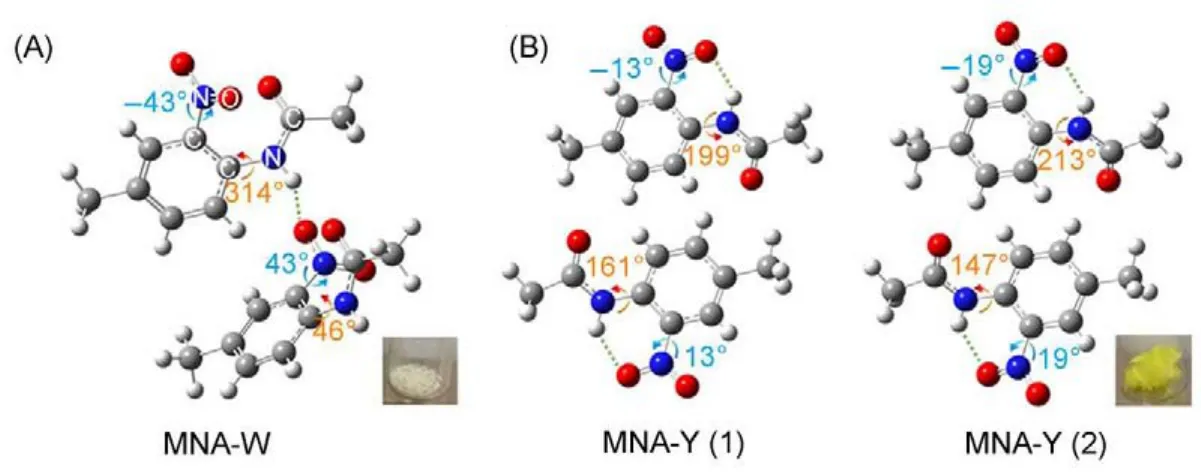
图3 MNA分子在(A)白色晶体与(B)黄色晶体中的分子构型64Fig.3 Molecular conformations of 4′-methyl-2′-nitroacetanilide(MNA)in(A)the white crystal,and (B)the yellow crystal64

图4 (A)MNA白色晶体的分子傅里叶变换红外光谱；(B)振动跃迁偶极矩夹角测量方法示意图64Fig.4 (A)Fourier transform infrared(FTIR)spectrum of MNAin the white crystal; (B)illustration of how the vibrational cross angle between two modes being experimentally determined64

3.1.1 振动跃迁偶极矩夹角的测量

图4(A)所示为MNA白色晶体的分子红外吸收光谱，其中几乎每一个峰都对应于MNA分子的一个振动模式。例如在1362 cm－1处的吸收峰对应于硝基上NO2基团的拉伸振动vs(NO2)，而1672 cm－1处的吸收峰对应于酰胺上C＝O键的拉伸振动v(CO)。这些振动模式分布在分子不同的化学基团上，并且每一个振动模式都对应于一个有特定空间取向的跃迁偶极矩。跃迁偶极矩之间的相对空间取向则由分子的整体三维空间构型所唯一确定。这也就意味着，如果我们能在实验上确定每对振动跃迁偶极矩间的相对夹角，便可以得到分子的空间构型信息。以测量vs(NO2)与v(CO)之间的相对夹角为例，如图4(B)所示。由于分子内两个振动模式之间往往存在着一定的非简谐耦合96，其中一个振动模式的激发往往会导致另外一个振动模式的频率发生一定的位移，进而反映在多维振动光谱的信号中。因此，在实验中，我们首先采用一束中心波长在1362 cm－1附近的线性偏振脉冲激光去激发样品中NO2基团的拉伸振动。紧接着，在非常短的时间内(约0.1－0.2 ps)，用另外一束中心波长在1672 cm－1附近的线性偏振脉冲激光同样去照射样品，便可以探测C＝O键拉伸振动的响应，得到两个振动模式之间的耦合信号。信号强度的大小与两束激光的相对偏振以及两个振动跃迁偶极矩之间的夹角直接相关。因此，通过改变两束激光的偏振，便可以确定vs(NO2)与v(CO)之间的夹角大小。进一步地，通过分别扫描激发脉冲和探测脉冲的频率，便可以得到一幅覆盖有多个振动模式的多维红外光谱图，见图5(A)。图中每一对红峰和蓝峰都代表一对振动模式的耦合信号，从中可以得到这两个模式的空间夹角。通过分析这些大量的夹角信息，便可以构建出分子的三维空间构型。

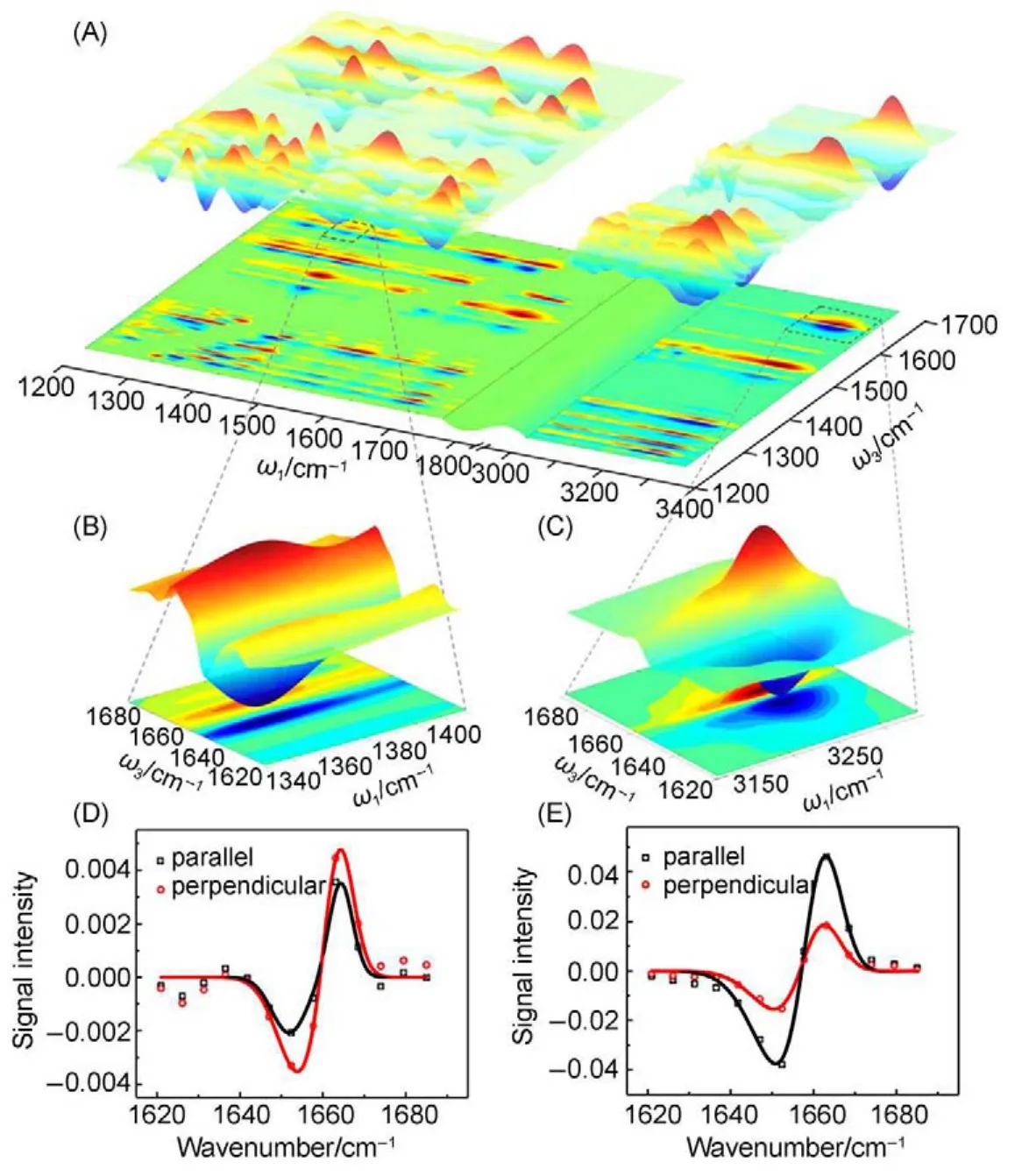
图5 测量不同振动模式的相对空间夹角64Fig.5 Determine cross angles between different vibrational modes64

首先，让我们分析图5(B)所示的一对耦合峰。其中红峰的激发频率对应于ω1=1362 cm－1，即vs(NO2)的0－1(基态到第一激发态)跃迁，而探测频率对应于ω3=1672 cm－1，即v(CO)的0－1跃迁。说明了此信号来源于激发硝基上NO2基团的拉伸振动后，因与酰胺上C＝O键的拉伸振动之间的相互耦合所引起的后者频率发生位移。而蓝峰的探测频率对应于ω3=1555 cm－1，表明了频率位移的方向与大小。如图5(D)所示，耦合峰的信号强度大小与激发光和探测光的相对偏振有关。如果假设在激光探测范围内(光斑直径约几百微米)的样品分布是各向同性的，我们便可以直接得到在不同相对激光偏振下测量得到的信号强度的大小与相应的两个振动跃迁偶极矩空间夹角的关系式61,97：

其中，I‖与I⊥分别代表在激发光与探测光的偏振平行或垂直条件下所测得的信号强度。θ为信号所对应的两个振动模式跃迁偶极矩的相对空间夹角。这样，如图5(D)所示，通过分别测量偏振平行及垂直条件下耦合信号的大小，并利用公式(1)，我们就可以计算出，NO2基团的拉伸振动与C＝O键的拉伸振动之间振动夹角为70°±2°。进一步地，利用同样的方法我们可以得到分布在MNA分子上各个化学键和基团的振动模式(如v(CO)、vs(NO2)、v(NH)、vas(NO2)、vs(C＝C)，等等)在空间上的相对夹角64。

3.1.2 将振动夹角转为空间夹角

由于MNA分子的空间结构主要取决于前面所述三个分子平面的相对夹角，因此下一步需要将实验中所测量得到的振动模式空间夹角转化三个平面相交所形成的两个二面角，即图3中定义的两个二面角∠CC/NO和∠CC/NC。基于密度泛函(DFT)方法，可以通过将两个二面角固定为任意数值来计算出相应分子构型下每个振动模式跃迁偶极矩的空间取向。并且对任一分子构型，每一对振动模式之间的夹角是唯一确定的。理论计算结果表明，分子振动模式的空间夹角非常依赖于分子三维空间构型的选取。具体来说，当将NMA分子中两个二面角∠CC/NO和∠CC/NC从0°变换到360°时，一些振动模式之间，如v(CO)与vs(NO2)，的夹角可以从0°变换到90°。但两者之间的关联并不是一一对应的：尽管每对固定的二面角对应于唯一的振动夹角，但是不同的二面角有可能会对应于相等的振动夹角64。因此，为了尽量得到唯一的分子构型，我们需要同时考虑尽可能多的振动夹角，尤其是那些对分子构型依赖性很强的振动夹角。基于这些振动夹角对分子构型的依赖性不同，当选取的数量足够多的时候，便可以唯一确定出分子的空间构型。从图5所示的测量结果中，我们共选取了15对振动模式，包含有CH、NO2、C＝O、C＝C及NH等化学键的振动，它们对两个二面角的变化有着截然不同的依赖关系。通过将这15个角度数值与理论计算的结果相对比，就可以确定出分子的构型。在实际操作中，考虑到分子的对称性，我们将二面角∠CC/NO从－80°变换到90°，而二面角∠CC/NC从0°变换到350°，步长间隔都为10°。对于每一对固定的二面角，分别计算相应分子构型下所有振动夹角的数值，并代入到如下公式64：

结果如图6(A)所示，通过代入15对振动模式夹角的计算以及实验数值，我们得到了对应于不同二面角∠CC/NO与∠CC/NC下的Er(x,y)数值分布。图中用白色方块所标记出来的位置即表示两个全局数值最小点，分别对应于两个彼此镜面对称的分子构型(∠CC/NC,∠CC/NO)=(50°,40°)和(310°,－40°)。由此认定，这两对二面角所对应的分子构型即为实验测量得到的MNA白色晶体中最可能的分子构型。而利用XRD测量的结果表明，这两个二面角的数值为(46°,43°)和(314°,－43°)，与上述数值非常接近，表明了利用多维振动光谱技术测量分子三维空间构型的可行性以及准确性。

利用同样的方法，我们也可以测量MNA黄色晶体中分子的构型。但这里需要额外考虑的是，在这种晶体中有两种不同分子构型的存在，MNAY1和MNA-Y2。如果直接采取上述方法，我们将得到的是两种分子的平均构型。但是通过对样品红外吸收光谱的测定可以发现，晶体中这两种分子所对应的NH键的振动频率和C＝O键的振动频率是不同的：MNA-Y1对应于(3360 cm－1,1709 cm－1)；MNA-Y2对应于(3383 cm－1,1720 cm－1)64。由于在实验中所测量得到的信号峰将主要来自于分子内的振动耦合62，因此，所有测量到的与这两个振动模式有关的夹角都可以通过激发或探测频率的差异被明确指认为来源于哪种分子的贡献，进而可以将实验测得的所有振动夹角分为两组，并分别利用上述方法求解各自的分子构型。图6 (B)和(C)分别表示在MNA-Y1和MNA-Y2中对应于不同二面角∠CC/NO与∠CC/NC下的Er(x,y)数值分布图。从中我们可以确定MNA-Y1所对应的两个最可能的构型为(∠CC/NC,∠CC/NO)=(150°,20°)和(210°,－20°)，而MNA-Y2所对应的两个最可能的构型为(∠CC/NC,∠CC/NO)=(160°,30°)和(200°,－30°)。同样，与利用XRD方法得到的结果(图中红点所示)非常相近。

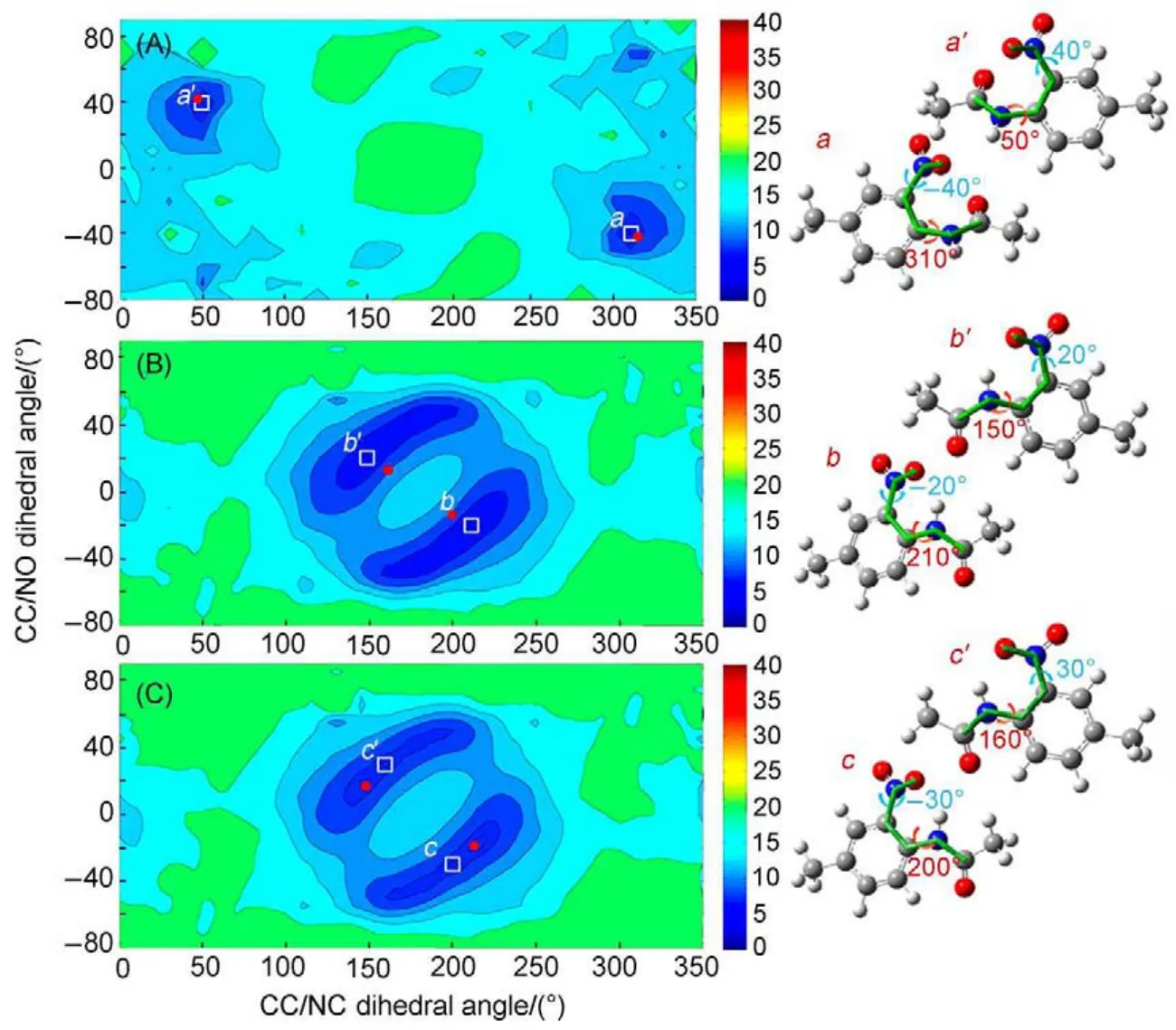
图6 样品(A)MNA-W，(B)MNA-Y1以及(C)MNA-Y1中对应于不同二面角∠CC/NO与∠CC/NC的Er(x,y)的数值64Fig.6 Average Er(x,y)values with different∠CC/NO and∠CC/NC dihedral angles for(A)MNA-W, (B)MNA-Y1,and(C)MNA-Y264

在这里我们需要注意的是，上面所用到的振动夹角都是指分子内简正模式的振动夹角，也即对应于利用DFT计算所得到的各个简正振动模式，与分子的红外吸收光谱相对应(费米共振等特殊情况除外)。但由于振动耦合强度与振动模式间的相对距离有极强的依赖关系，当分子体系的尺度非常大的时候，一些简正振动模式通常会离域到分子上较大的空间，此时两个简正模式的耦合可以认为主要由靠得很近的两个局域模式的耦合所决定。这样，在实验上通过测量分子振动耦合所得到的振动夹角，应当会退化为相应两个局域模式的振动夹角，进而可通过上述方法转化为分子局部的空间夹角。利用这一点，我们可以将一些复杂的分子体系空间构型的求解逐步简化为各个局部构型的测量。这将会在将来的工作中进一步证明和讨论。

3.1.3 液态环境下MNA分子构型的确定

相比于XRD方法，多维振动光谱技术的一个重要优势是它的测量范围可以覆盖几乎所有的凝聚态体系，例如溶液状态下甚至于熔融状态下MNA分子的构型。图7(A)中列出了在四类不同的液态样品中，对应于不同二面角∠CC/NO与∠CC/NC下的Er(x,y)数值分布图。这四种样品分别为：(1)室温下MNA分子在CCl4中的0.01 mol·L－1稀溶液，此时MNA分子内的氢键作用要远强于溶质－溶剂间的相互作用；(2)在100°C熔融状态下的MNA分子，此时MNA分子内的氢键作用与相邻MNA分子间的氢键作用同时存在；(3)65°C下2 mol·L－1水-乙醇过饱和溶液，此时白色晶体开始结晶；(4)室温下在CCl4中的0.3 mol·L－1饱和溶液，此时黄色晶体开始结晶。结果表明，在这四种完全不同状态下的样品中，MNA分子最可能的空间构型基本相同，即以共平面构型为中心，(∠CC/NO,∠CC/NC)=(180°,0°)，有一定范围的空间分布，如图7(B)所示。分子动力学模拟也给出了非常类似的结果，如图7(C)所示，有多于一半的MNA分子构型与共平面构型所对应的两个二面角相差在30°以内。上述结果表明，即便是在即将析出晶体的过饱和溶液中，MNA分子的主要空间构型也与其在相应晶体中的完全不同。这个结论将有利于我们将来深入了解分子晶体结晶过程中的微观分子动力学行为。

图7 液态环境下MNA分子的空间构型64Fig.7 Molecular conformations of MNAin liquids64

最后我们需要注意，对于MNA分子，无论是在晶体样品中还是溶液样品中，我们都采用公式(1)来确定两个振动模式跃迁偶极矩的相对空间夹角。在这里有两点需要考虑：一方面，待测的MNA分子晶体是以粉末的形式存在。因此尽管在每个晶粒内部分子取向并不是随机的，但在整个激光探测的区域内，各个晶粒的取向是随机分布的，从而保持了公式(1)的有效性。而如果在探测区域内分子的取向不是随机分布，例如一块单晶样品，则需要根据晶体的空间取向详细计算出各向异性数值与振动跃迁偶极矩空间夹角的关系；另一方面，由于有分子转动或共振能量转移的存在会导致R(t)值随时间进行衰减，为了尽可能准确地获得跃迁偶极矩的空间夹角，时间值应尽量选择在接近时间零点的位置。例如，上述实验采用的探测时间为光激发后的0.2 ps。

3.2 应用实例

3.2.1 金属纳米粒子表面分子构型的解析

在过去几十年里，金属纳米粒子已经被人们广泛研究，并已应用到催化、生物学过程、纳米光电装置等等各个领域98－105。对吸附在金属纳米粒子表面分子的空间构型以及能量动力学的深入研究，将有助进一步推动它们在实际中的应用105－107。但在这类问题面前，一些传统的测量手段显示出了很多的局限性。为此，我们利用多维振动光谱技术测量了吸附在3.5 nm金粒子表面的4-羟基苯硫酚(p-HO-C6H4-SH)分子的空间构型，证明了此方法可以有效到应用到此类问题的解析之中68。如图8所示，4-羟基苯硫酚分子可以与金表面的原子形成相对较强的硫―金键，因此，对于这类系统的一些研究结论也可以直接应用到分子导线与电极间的接触体系之中108。

图8 吸附在3.5纳米金粒子表面的4-羟基苯硫酚分子构型示意图以及测量得到的多维振动光谱图68Fig.8 Molecular conformation and vibrational dynamics of 4-mercaptophenol on the 3.5 nm gold nanoparticle surface probed with multiple-mode multiple-dimensional infrared spectroscopy68

对于这样的一个分子体系，我们首先需要考虑的是，在金属纳米粒子的影响下如何计算分子的振动模式以及它们之间的夹角。根据文献109－111，3.5 nm的金粒子已经显示出明显的金属性质。此外有些证据表明，在一些干净的金属表面，电子会与吸附的分子有着极强的耦合，从而会导致玻恩-奥本海默近似(BOA)的破坏112－114。进而在金属导带内连续电子能级间的电子-空穴跃迁会与表面分子的核运动耦合在一起，使得分子的振动能量以一定的速度向金属发生转移。但是，如果假设这种非绝热电子-振动耦合作用与分子内的振动耦合相比很小的话，我们在计算中就可以忽略非绝热电子-振动耦合的影响，进而可以在计算中减少金属原子的个数以简化计算过程。为了证明这种假设的合理性，我们首先测量了3.5 nm金粒子表面的4-羟基苯硫酚分子各个振动模式第一激发态的寿命，包括有O―H键、C＝C键、C―H键，以及C―O键等等68。并将这些结果与在纯4-羟基苯硫酚分子晶体中，以及在CCl4溶液中所测量得到的结果进行对比。结果表明，除了C―O键拉伸振动的寿命略有缩短外(可能源于费米共振的影响)，其它各个振动激发态的弛豫时间在上述三种环境下基本保持不变，证明了因电子-振动耦合作用所导致的振动能量弛豫在这里可以忽略不计。这也与理论计算结果保持一致：由表面非绝热电子-振动耦合所导致的振动弛豫时间与上述测量到的振动态寿命相比要小于近两个数量级。因此，在接下来对分子振动模式的计算之中，我们可以直接采用玻恩-奥本海默近似，将金纳米粒子简化成三个金原子。我们开展了一系列的实验来考察玻恩-奥本海默近似在金属纳米颗粒表面的成立条件115。

接下来便是通过多维振动光谱技术测量大量的分子振动夹角并进一步转化为分子的空间构型。对于金纳米粒子表面的4-羟基苯硫酚分子，其构型主要由两个自由度决定：(1)羟基相对于苯环的转动；(2)苯环相对于硫-金键的转动。通过改变这两个自由转角，计算相应构型下分子振动模式之间的夹角，并与在实验中测得的16对振动夹角进行对比，便可以最终得到纳米金粒子表面的4-羟基苯硫酚分子的空间构型，如图9所示68。结果表明，羟基相对于苯环平面有50°－60°的转动，而苯环相对于硫-金键有约20°的转动。其中，羟基相对于苯环平面的偏离可以归结为几种表面几何约束作用相互竞争的结果，包括有π－π堆叠以及氢键疏水作用等。

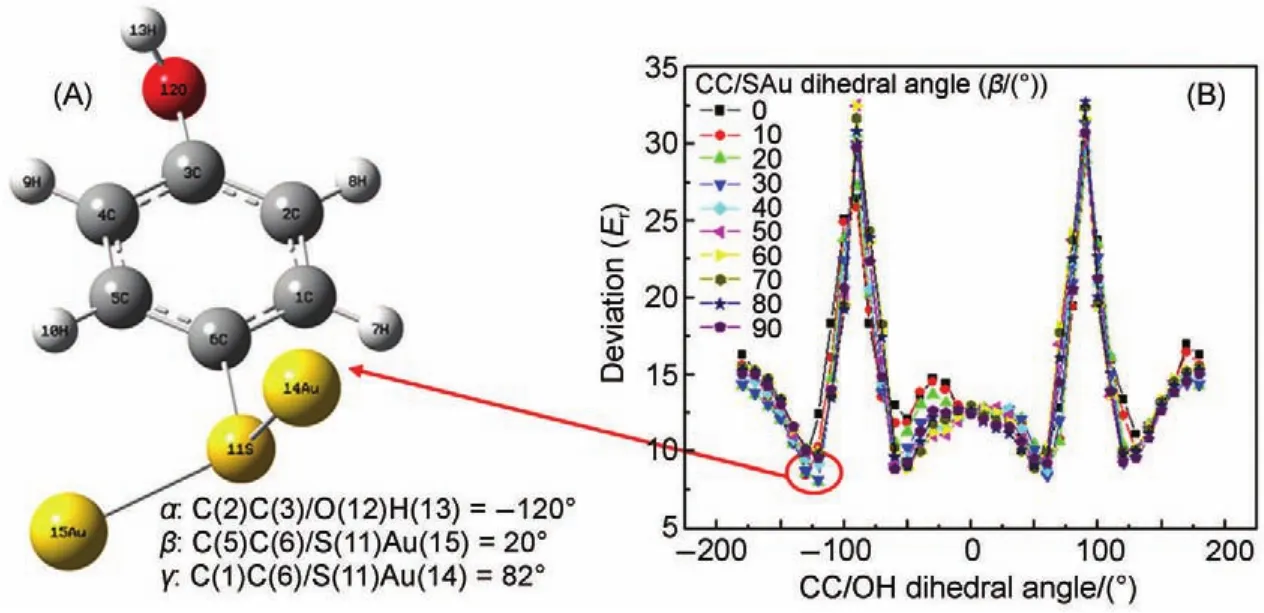
图9 3.5纳米金粒子表面的4-羟基苯硫酚分子空间构型的确定68Fig.9 Determining the molecular conformation of HOC6H4-S(Au)2on the surface of 3.5 nmAu nanoparticle68

3.2.2 氨基酸分子构型的测定

在很多生物学过程中，蛋白分子的构型变化起着至关重要的作用。例如一些催化反应，细胞信号传导，生物膜的融合等等81,82,116,117。这里，我们以L-半胱氨酸分子为例，证明如何通过多维振动光谱技术解析组成生物蛋白的基本单元——氨基酸分子的空间构型63。与前面两个体系相比，在氨基酸分子的构型解析过程中所面临的一个重要问题就是相对较多的自由度。对于L-半胱氨酸分子来说，如图10所示，它有四个主要的自由度。这样，如果按照之前的方法，将每个自由度对应的转角从0°扫描到360°，并以10°为间隔。最终将面临的是364=1679616种分子构型的计算，其工作量是十分惊人的，并且极其费时。因此需要考虑一些策略以及近似条件来减小构型空间的搜索范围。具体来说，基于所测量的大量振动模式之间的夹角对二面角β和γ依赖性很大，我们首先忽略另外两个自由度的影响，而只计算改变这两个二面角所导致的分子振动模式的变化，并与实验结果进行对比，便可以得到β与γ的大概角度。进一步地，再通过固定β的数值，搜索α和γ空间转角，利用同样的方法可以确定出α的数值。最后再利用S―H键所对应的振动模式与分子上其它振动模式间的夹角确定出二面角δ的数值，最终构造出L-半胱氨酸分子在晶体中两种不同的空间构型，如图10所示。这里需要注意的是，对于γ和δ转角的确定，需要涉及到氢原子的位置。但是由于氢原子本身较小的散射截面，使得XRD等散射的方法无法对其很好的确定。而利用多维振动光谱技术可以很好地解决这一问题，通过对这些转角的测量，将会对氨基酸或蛋白分子所形成氢键性质的研究提供非常重要的信息63。

3.2.3 分子间相对空间取向的测量

在前面几个实例中，通过测量分子内不同振动模式跃迁偶极矩间的相对夹角可以得知分子的三维空间构型信息。其中分子内的振动夹角通过式(1)来确定，或者也可以写成如下形式：

其中R(t)=(I‖－I⊥)/(I‖+2I⊥)是随时间变化的各向异性数值，而θ(t)的定义则为在t时候所探测的振动模式跃迁偶极矩与在零点时刻所激发的振动模式跃迁偶极矩的空间夹角。只有当时间t选取在零点附近时，例如0.2 ps，由上式所计算的角度θ(t)才真正表示分子内振动模式间的夹角。这里需要注意的是，分子间的振动模式耦合作用往往很小，可以忽略不计。但当时间较长的时候，有两个过程需要考虑，一是分子自身会随时间发生一定的转动，这一点在溶液中极为明显。由此，探测到的振动模式的空间取向也会随之改变。另一方面，分子的振动激发态往往都寿命较短，通常仅有几个皮秒。在此之后，振动能量会弛豫到分子内以及周围环境中较低的振动能级，最终转化为热量，扩散到周围的分子中。这种以热量形式存在的低频振动同样也会与分子内相对能量较高的振动能级发生耦合，进而改变后者的振动频率，在多维振动光谱中贡献信号118－120。但是由于热能的传递，此时所探测到的振动模式已经既包含有原激发分子内的振动，同时也含有邻近分子的振动，如图11所示。换言之，此时根据实验测量的R(t)所计算出的角度θ(t)将会获得邻近分子间相对空间取向的信息，具体做法可以参看相关工作62。

图10 利用多维振动光谱技术测量L-半胱氨酸晶体中的分子空间构型63Fig.10 Molecular conformations of crystalline l-cysteine determined with vibrational cross angle measurements63

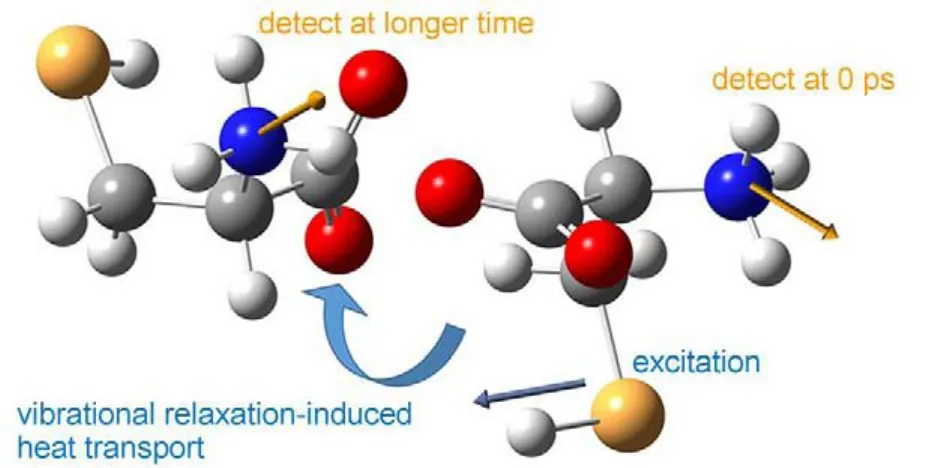
图11 利用热能传递过程测量分子间的相对空间取向Fig.11 Relative intermolecular orientation probed via molecular heat transport

一个完整的分子结构包括分子三维构象与化学键间的距离。上面介绍了确定构象的方法。下面将介绍我们为解析分子间短距离而发展的分子尺方法。

4 精度为埃的“分子尺”

分子之间在瞬时内的短程相互作用在很多化学反应和生物学过程中扮演着非常重要的角色，例如在水溶液中离子与离子间的相互作用，膜蛋白上的离子与蛋白相互作用，以及酶和底物的相互作用等。如果能够在超快的时间尺度上测量分子之间的距离，并达到极高的空间分辨精度，将会使我们更加深入地了解这些化学以及生物学过程。在过去的几十年里，人们已经利用荧光共振能量转移技术(FRET)来研究分子之间的距离与相互作用121,122，即基于荧光能量给体与受体间通过偶极-偶极相互作用并以非辐射方式转移电子态能量的过程，建立起能量转移的速率(或荧光的量子产率、荧光强度、荧光寿命等)与给-受体之间的距离关联。对于这种方法，一方面需要待测体系中有合适的荧光给体与荧光受体探针连接于待测分子上，这就限制了此方法的应用对象范围；另一方面，这些探针分子的尺寸通常有1－2 nm，甚至于更大。这样不仅会限制了待测对象的距离只能在更大的空间尺度，同时探针分子本身对待测分子间相互作用的影响也不容忽视。

究其原因，在FRET方法中，空间的测量是基于电子态的能量传递过程，而其测量精度也必然会受相对较大的电子能量传递载体的限制。但是，如果将测量对象转为振动能量的传递，上述遇到问题将都会避免。同FRET方法类似，分子内所包含的振动模式经光激发后，所获得的振动能量也同样将会传递给周围分子的振动模式，而振动能量的传递速率也同样与分子间的距离密切相关。如果我们能够在实验上测量分子间振动能量传递的速率，并在理论上推导出传能速率与分子间距的关系，将会得到分子之间的距离信息。但与FRET方法不同，一方面，几乎所有分子体系本身就包含有大量的振动模式。这样，无需额外的探针分子，就可以得到待测分子间的能量传递信息；另一方面，振动能量的载体甚至可以小至一个化学键，尺寸只有1－2 Å(1 Å=0.1 nm)，这样就可以允许我们测量极短的分子间距。这种基于振动能量传递过程测量分子间距的办法有望发展成为精度为埃的“分子尺”来研究各种凝聚态分子体系中的瞬态分子相互作用过程58－60,65。

4.1 振动能量转移速率的测量

根据振动能量传递过程中能量的给体与受体的振动能级差值，可以将传能过程简单地区分为两类：(1)共振能量转移，即给体与受体的振动能级相同；(2)非共振能量转移，即给体与受体的振动能级不同。对于这两种传能过程，在实验中有着各自的测量手段。这里，我们以对饱和(10 mol· L－1)硫氰酸钾(KSCN)水溶液中的振动能量转移过程的测量为例，分别介绍这两种测量方法。

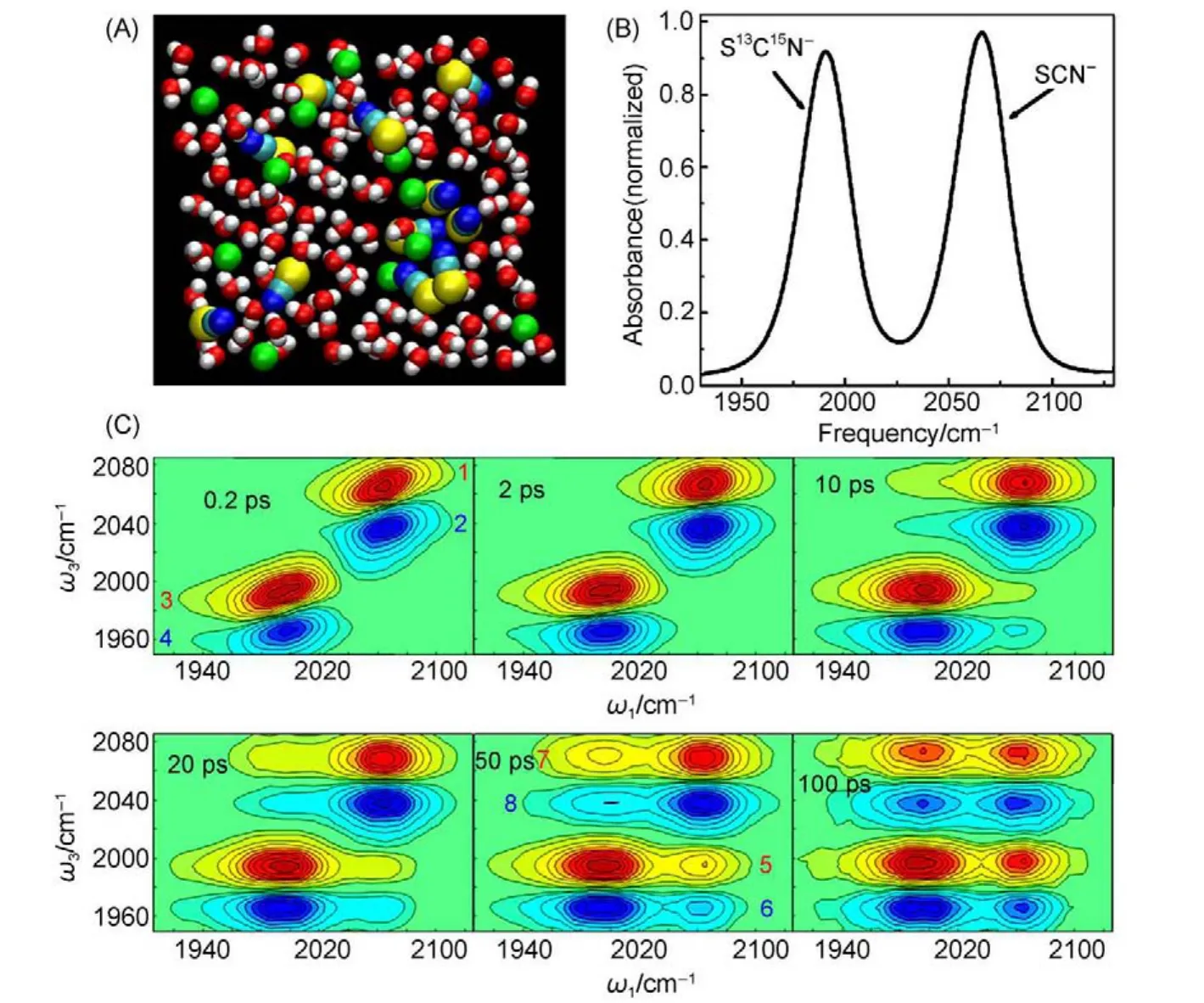
图12 超快非共振能量转移过程的观测72Fig.12 Observation of ultrafast nonresonant energy transfer72

4.1.1 非共振能量转移

分子或是离子之间的非共振能量转移过程可以利用超快多维振动光谱技术来直接观测70,72,123。图12(a)为分子动力学模拟计算得到的1.8 mol·L－1的KSCN水溶液微观结构示意图72。可以看出，由于SCN－

阴离子的浓度较高，部分离子倾向于聚集在一起形成团簇。这样，振动能量便可以在相邻的离子间进行交换。为了方便测量离子间的非共振能量转移过程，我们将其中一半的SCN－阴离子替换为含同位素标记的S13C15N－阴离子。同位素的作用可以将C≡N键振动的基态到第一激发态(0－1)的跃迁频率从2066 cm－1(SCN－)位移至1991 cm－1(S13C15N－

)，如图12(b)所示。通过超快多维振动光谱技术，我们可以直观测振动能量在这两种离子之间的交换过程。见图12(c)，在光激发后较短的时间(例如200 fs)，振动能量传递的过程还几乎没有发生。这时候在光谱中仅能看到两对对角峰1－4，其中峰1和峰2分别表示的是SCN－中C≡N键振动的0－1跃迁与1－2跃迁，而峰3和峰4分别表示的是S13C15N－中13C≡15N键振动的0－1跃迁与1－2跃迁。而随着光激发后时间的增加，振动能量将会开始在两种离子间进行交换。例如在50 ps的时候，我们可以看到非对角元上出现四个明显的信号峰5－8，便是来源于振动能量的转移。其中，峰5和峰6对应的激发频率为2066 cm－1(C≡N键振动的0－1跃迁)，而相应的探测频率为1991和1966 cm－1(13C≡15N键振动的0－1跃迁和1－2跃迁)，因此我们可以认定峰5和峰6来源于振动能量由SCN－离子向S13C15N－离子的转移。同样地，峰7和峰8来源于振动能量由S13C15N－离子向SCN－

离子的转移。在每一个固定的时刻，峰5和峰6的强度总是略大于峰7和峰8的强度。这可以利用细致平衡原理来解释，即能量从一个高能级传向低能级总是会快于从低能级向高能级的传递过程。这两个过程的速率之比是由波尔兹曼(Boltzmann)因子决定的：kDA/kAD=exp[(ωD－ωA)/RT]。其中，ωD－ωA表示能量传递的给体(D)与受体(A)的能级差值。

通过分析各个非对角峰的强度随时间的变化(见图13)，便可以得到振动能量在相邻两个不同的离子间传递的速率。为此我们需要构建一个动力学模型，以便定量化地分析实验数据中所包含的传能速率等物理量。具体分析如下：由于此时溶液是饱和的，按前面所述，很多离子将会不可避免地聚集在一起形成团簇。我们可以将水溶液中的硫氰酸根阴离子分为两类：一是处于团簇中的阴离子，振动能量可以彼此间高效地进行转移；另一类是其它被水分子分隔开的游离的阴离子，由于彼此间距离较远，能量转移几乎无法发生。这两类硫氰酸根阴离子的振动频率几乎相同，因此我们无法从光谱上进行区分。例如，在图12(C)中的对角峰1和2就同时包含有上述两类阴离子C≡N键振动的共同贡献。但是对非对角峰来说，由于反映的是离子间振动能量的传递，因此信号主要来源于处于团簇中的阴离子的贡献。基于对角峰与非对角峰信号来源的区别，我们便可以通过同时分析它们随时间变化的动力学过程从而得到振动能量在不同离子间交换的速率常数，并且还可以得到处于团簇中的与游离的阴离子数量的比值。上述物理图像可以用如下能量转移及位置交换动力学模型来表示61,72：

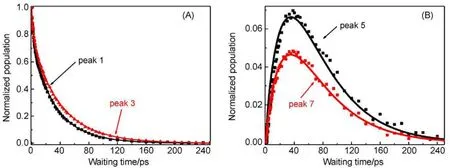
图13 在图12(C)中非对角峰的强度随时间的变化72Fig.13 Waiting time-dependent intensities of peaks 1,3,5,and 7 in Fig.12(C)72

4.1.2 共振能量转移

还以饱和KSCN水溶液为例，在形成的每一个离子团簇内，振动能量不但可以在不同的阴离子间(SCN－与S13C15N－)进行非共振转移，同时也会在同类的阴离子间(例如S13C15N－)共振传递。在实验部分中已经提及，共振能量转移速率可以通过测量分子振动态的各向异性弛豫来确定。为了将实验中所测得的各向异性弛豫速度与共振能量转移速度定量地关联起来，我们需要考虑两点：一是在这种体系中，各向异性弛豫的来源有两种，即共振能量的转移与分子自身的转动；另外，共振能量传递的给体将振动能量传递给受体后，同时也会接收其它受体的能量，其结果将会导致各向异性数值的恢复。考虑到以上两点，我们便可以构建适当的物理模型，并推导出如下关系式来定量分析离子间的共振能量转移过程66,72：

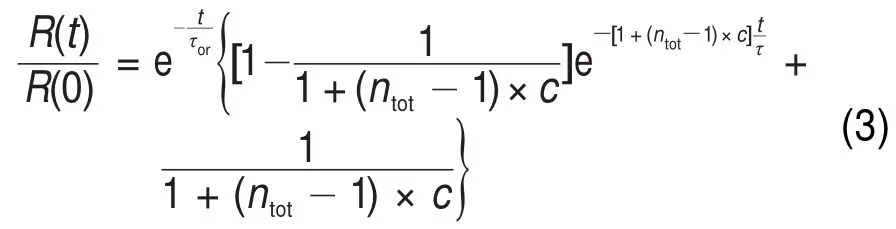
图14 在不同KS13C15N/KSCN摩尔比的10 mol·L－1硫氰酸钾水溶液中，S13C15N－离子上13C≡15N键振动信号的各向异性弛豫曲线72Fig.14 Anisotropy decay data(dots)of the13C≡15N stretch pump/probe signal of S13C15N－in 10 mol·L－1aqueous solutions with different KS13C15N/KSCN molar ratios72

我们不妨先把S13C15N－看作是振动激发态能量的载体，则τor代表在团簇中S13C15N－离子转动的时间常数；c表示S13C15N－离子在溶液中所有阴离子中(SCN－及S13C15N－)所占的浓度比值；n表示团簇

tot内每个能量传递单元中所包含阴离子的数目；τ表示振动能量从一个给体离子共振传递给另一个给体离子的时间常数。通过改变同位素标记阴离子的浓度c，我们便可以在实验上测到多条各向异性值R(t)/R(0)随时间衰减的曲线，如图14所示。可以看出，当KS13C15N的浓度较低时，不同的S13C15N－离子之间间隔较远，振动能量转移速度较慢，因此R(t)/R(0)随时间衰减也会相对较慢。而当KS13C15N的浓度较高时，例如在100:0溶液中，不同的S13C15N－离子之间将会靠得很近，振动能量转移速度很快，对应于R(t)/R(0)随时间的衰减明显加快。利用式(3)对所有曲线同时进行拟合，便可以得到三个未知变量的数值，即τor、ntot和τ。

其中，团簇中S13C15N－离子转动的时间常数τor可以由1%KS13C15N(1:99(摩尔比))所对应的各向异性弛豫曲线来直接获得。这是因为在此溶液中，S13C15N－离子所占的比例非常小，在每个离子团簇中，几乎最多只能存在一个。因此，每个S13C15N－离子几乎无法将能量共振传递给其它的S13C15N－离子。此时所测量得到的R(t)/R(0)值随时间的衰减将仅来源于S13C15N－离子自身的转动。这样，通过指数拟合，我们便可以直接得到离子转动的时间常数：τor=(10.0±1.0)ps。仅剩的两个未知变量将会很容易从对所有曲线进行的同时拟合中获得，并且我们由图14可以看出，公式(3)与实验结果拟合得非常好。最终结果表明，团簇内每个能量传递单元中所包含阴离子的数目为ntot=18± 3，以及振动能量从一个给体离子共振传递给另一个给体离子的时间常数为τ=(54±8)ps。因此，在纯KS13C15N溶液中，即KS13C15N:KSCN摩尔比为100:0时，一个阴离子向一个能量传递单元内所有其它阴离子的传能时间常数约为τ/ntot≈3 ps。而在KS13C15N:KSCN摩尔比为50:50的溶液中，由于共振传能受体的个数约减少了一半，因此相应的时间常数约为6 ps。这里需要强调的是，每个振动能量传递单元并不等同于每个离子团簇。通常一个较大的离子团簇中将会包含有多个能量传递单元，但在较稀的溶液中，由于每个离子团簇都非常地小，因此可以将它等同视为一个能量传递单元，上述结论将会在后面再次提及。

4.2 分子间距的确定

当在实验上确定出不同分子间或离子间的振动能量转移速率后，接下来要面对的一个重要问题就是如何将它与分子间的相对距离关联起来。这个问题的解答事实上将会涉及到一个非常基本的物理化学问题，即振动能量转移的微观机理是什么？在自然界中，几乎所有的化学反应以及生物学过程都伴随有振动能量的产生。振动能量从分子的一个能级转移到其它能级，或是从一个分子转移到另一个分子上，是凝聚态体系中一个最基本的分子现象70,123－129。对能量转移过程中分子机理的研究，无论是电子态的，还是振动态的，几十年间一直没有中断130－136，并始终存在着许多困惑与争议。大体上，分子间的能量转移过程可以分为两类。如果能量转移的给体和受体之间的耦合作用非常强(强度大于或等于去相干线宽60)，能量将会在分子间以相干(coherent)的形式进行传递60,137,138。而如果给-受体之间的耦合作用较弱(强度小于去相干线宽60)，能量将会以跳跃(hopping)的形式从一个分子传递到另外一个分子上60,137。在凝聚态体系中，对绝大多数的分子间振动能量传递过程而言，其中的给体和受体之间的耦合作用通常相对较弱，可以用能量跳跃模型来进行59,60。因此在本文中将只讨论后面这种情况的理论处理与实验验证。

4.2.1 共振及非共振传能机理

在凝聚态体系中，由于分子每时每刻都在不停的运动以及相互碰撞等，分子的振动频率将不是单一的数值，而是在能量空间有一定的分布。当能量传递的给体与受体的能量相同，即发生共振能量传递时，此传能过程将主要由退相位机理(dephasing mechanism)所决定59,60。其物理图像如下：由于能量传递的给体与受体所包含的振动态因偶极-偶极相互作用耦合在一起，从而形成一个相干的叠加态。如果没有任何外界干扰，激发态能量将会在给体的振动态与受体的振动态之间以相干的形式不断地相互交换。但在凝聚态体系中，由于分子热运动的存在，相互碰撞总是不可避免，而这种碰撞往往会瞬间改变分子的振动频率，从而会导致给体与受体这对分子间的相干性被破坏，对应于相干态的退相位过程。而退相位的结果就是，给体所携带的振动能量将有一定概率存在于受体的激发态上，并且不再回传，由此完成了一次能量传递过程32,33。考虑到退相位过程的发生在时间上将会有一定的概率分布，将所有这些退相位过程在时间上作个积分，便可以得到振动能量传递速率kDA的解析表达式59,60：

在式(4)中，ΔωDA=ωD－ωA表示能量传递的给体(D)与受体(A)的中心能级间隔，当间隔为零的时候，即表示共振能量传递过程；τ表示能量传递给-受体的相干退相位时间；VDA代表给-受体之间的耦合强度60，在以分子偶极－偶极相互作用为主的条件下，可以表示为122：

其中，n为折射系数；ε0是真空介电常数；μD和μA代表给-受体各自的振动跃迁偶极矩；rDA为给-受体分子之间的距离；κ是取向因子，既由给-受体间的相对取向决定，也与给-受体间相对转动速度的快慢有关59。以室温下水溶液中的离子为例，它们的转动速度往往都远快于两个离子间的振动能量传递速率。因此在计算耦合强度VDA时，κ值可以近似为在空间中所有可能相对取向的平均值60,72，即(2/3)1/2。最后，将公式(4)和公式(5)结合起来，我们便最终获得连接kDA与rDA的解析表达式。公式(4)的一个特例是著名的FRET传能公式60。

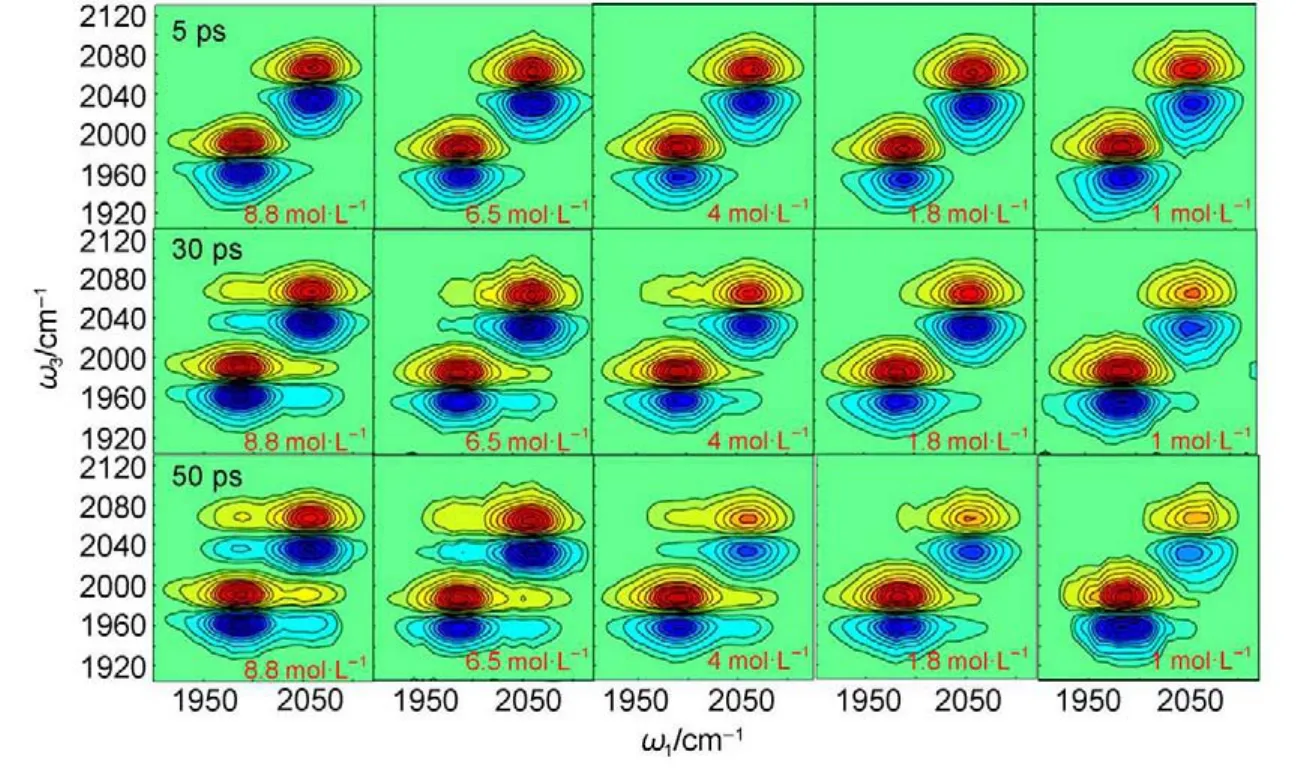
对于非共振能量传递过程而言，除了退相位过程，声子耦合作用也同样会在某些条件下起着非常重要的作用59,60,139－142。也就是说，在非共振能量转移过程中，有两种机制在同时起着作用：(1)在一个非共振能量传递系统里，由于振动能级的不断快速涨落，给体与受体的振动能量是有一定概率分布的，且总是有一定机率会达到重合。因此，尽管二者的能级中心位置不一样，但是振动能量总是可以通过给-受体间能量重合的那一部分分子由共振的方式传递过去。这种能量传递过程与前面所述的退相位过程是一样的，因此对应的传能速率可以用上述公式来确定；(2)同时，如果给-受体之间的能级间隔恰好与分子体系内的某一个声子的能量或几个声子能量的总和相等，振动能量在传递前后的能量差值便可以由声子的能量来进行补偿。即，如果给体的能级高于受体的能级，传能过程中将伴随有一个或多个声子的产生，其总能量恰好等于能级间隔ΔωDA。反过来，如果给体的能级低于受体的能级，传能过程中会伴随对一个或多个声子能量的吸收。这种非共振能量传递的形式便称为声子补偿机理。

在实际的凝聚态分子体系中，这两种传能机理往往会同时起着作用，振动能量将通过两个途径同时进行传递，其中传能速度相对较快的途径将起着主导作用。例如在KSCN晶体中，由于声子模式的大量存在，声子补偿机理将在能级间隔较大的非共振能量传递过程中起着非常重要的作用。而在KSCN的水溶液内，退相位机理则主导着非共振能量的传递过程58,60。我们最近的研究表明，在室温条件下的溶液中，若振动传能给-受体间的能级间隔远小于热能(ΔωDA

4.2.2 利用退相位模型确定分子间距

综上分析，对于在溶液中发生的大多数共振及非共振能量传递过程，以及在晶体中发生的能量间隔相对较小的非共振及共振能量传递过程都可以用退相位模型很好地进行描述。振动传能的速率常数则可以通过式(4)来表示，式中振动跃迁偶极矩以及折射率的数值很容易确定，但是还剩下两个未知参数，即退相位时间τ以及耦合强度VDA需要通过实验获得。在前面所述测量振动传能速率的方法中已经提及到，利用同位素标记的方法可以改变振动能级的位置，但同时保持其它所有的体系参数不变，这是因为同位素取代并不会改变体系的电子结构或是分子间的相互作用58,60,66。换言之，通过不同类型的同位素标记，我们可以改变式(4)中ΔωDA的数值，但同时保持其它参数不变。若将实验中测量得到的传能速率的数值与相应的ΔωDA值代入到方程中，我们便可以得到两组或两组以上的方程。由于未知变量仅有两个，因此便可以通过求解方程来确定退相位时间τ以及耦合强度VDA的数值。一旦VDA值确定，通过式(5)便可以最终得到分子之间的相对距离。

但是在有些分子体系中，同位素标记并不是能很容易实现。我们将会只能测量到一个固定能量间隔ΔωDA下的速率常数，得到一个含有两个未知量的方程。为了得到耦合强度VDA的数值，我们需要对退相位时间τ，或是退相位线宽τ－1做出个大概的估计。在方程(4)的推导过程中，我们已经证明给-受体间的相干退相位线宽一定不会大于单独的给体或受体自身的线宽之和τ－1 D+τ－1 A，其中τ－1 D和τ－1 A可以通过各自振动光谱的宽度来获得60。进一步说，如果给体与受体各自的退相位过程是彼此相关联的，则有τ－1<τ－1 D+τ－1 A。反之，如果二者并无关联，则有τ－1=τ－1 D+τ－1 A。在我们做过的所有关于硫氰酸盐水溶液中振动能量传递的实验中，结果都表明给体和受体的退相位过程是彼此相关的，由此导致相干退相位线宽τ－1约为给体或受体自身的线宽之和的50%－80%。这可能是因为在这些体系中，给体与受体之间的距离很近，通常仅有0.4 nm左右。因此其中任一个的退相位过程将会不可避免地对另外一个的退相位过程造成影响。仅有在给-受体之间的空间距离相对较远的时候，二者才不会相互关联，我们才可以得到τ－1=τ－1 D+τ－1A。值得注意的是，在此条件下，公式(4)则将会过渡到传统的Forster传能公式，即传能速率将由给体与受体的光谱重叠积分所决定60。综上所述，若待测分子间距较小，例如小于1 nm时，我们可以将τ－1 D+ τ－1 A值的50%作为退相位线宽τ－1的一个比较合理的初步估计。进而可以通过实验中所测量得到的振动传能速率估计出VDA以及分子之间的距离。

为了验证上述方法的可行性，我们利用此技术测量了KSCN晶体中相邻两个离子之间的距离，结果如图15所示59。通过共振能量转移的实验，可以得到在晶体中距离最近的两个离子之间能量共振传递的速率为kDA=27 ps。结合在非共振能量传递实验中所得到的结果，以及考虑到KSCN晶体的结构，可以得到式(4)和式(5)中所有的参数：ΔωDA=0，μD=μA=0.31 D，n=1.5，τ=0.66 ps，以及(<κ2>)1/2=0.378(考虑到晶体内离子的摆动过程)，从中便可以计算出晶体中相邻两个离子的C≡N键的距离为0.39 nm。而人们之前利用XRD的方法测量KSCN晶体的结果表明，这两个离子间的距离为0.4017 nm，与我们的测量结果非常接近。这一方面表明利用此方法计算分子间距的可行性与有效性，同时也表明利用分子间的振动能量传递过程测量分子间距，其精度甚至可以小于一个埃，远高于FRET等测量手段的空间分辨精度。

图15 利用共振能量传递测量KSCN晶体中的分子间距59Fig.15 Molecular distances in KSCN crystal determined with vibrational energy transfers59

4.2.3 应用实例——水溶液中离子间距的测定

在前面所介绍的对于饱和(10 mol·L－1)硫氰酸钾(KSCN/KS13C15N(1:1(摩尔比))水溶液的共振及非共振能量转移过程的测量之中，我们得到了共振转移速率为6 ps，以及非共振转移速率115 ps，分别对应于ΔωDA=0 cm－1以及ΔωDA=75 cm－1。根据公式(4)，可以得到给-受体之间的耦合强度VDA约为4.1 cm－1，以及相干退相位时间1/τ=15 cm－160。但是这里测量所得到的振动传能速率对应的是每个能量传递单元中一个给体阴离子向其它所有受体阴离子(约18/2=9个，见4.1.2节)传能速率的总和。因此VDA=4.1 cm－1代表的是给体阴离子与其它所有受体阴离子耦合强度的总和，而单个离子与单个离子间的耦合强度则为V1→1=VDA/91/2=1.4 cm－160,66。结合参数n=1.5，μD=μA=0.33 D以及<κ>=(2/3)1/2，我们便可以根据公式(5)得到在饱和硫氰酸钾水溶液内的每个离子团簇能量传递单元中，阴离子间的平均距离为rDA=0.51 nm60。这个数值明显大于KSCN晶体中相邻两个离子的间距(0.4017 nm)，这主要是因为0.51 nm仅是一个能量传递单元内一个阴离子与其它所有阴离子距离的平均值，在一个由18个阴离子组成的单元内，必然会有些阴离子相对距离较远。如果我们想要了解在这种水溶液里所形成的离子团簇中，相邻的两个阴离子到底可以挨得多近，则需要进一步测量较小的离子团簇中的振动能量传递过程。显然，这样的离子团簇将会存在于相对较稀的溶液中。当团簇内阴离子的个数不多于四个的时候，我们便可以近似认为此时所测量得到的阴离子平均间距约为相邻两个阴离子的距离。

图16 不同浓度的KSCN/KS13C15N(1:1(摩尔比))水溶液在三个不同时刻的多维振动光谱图72Fig.16 Multiple-dimensional vibrational spectra of KSCN/KS13C15N(1:1(molar ratio))aqueous solutions with different concentrations at three different waiting times72

表1 测量及计算得到的不同浓度下的KSCN水溶液中离子团簇的性质60,72Table 1 Experimental and MD simulation results of ion cluster properties in KSCN aqueous solutions at different concentrations60,72

图16所示为不同浓度的KSCN/KS13C15N(1:1)水溶液在三个不同时刻的多维振动光谱图72。可以看出，在同一个时刻，稀溶液所对应信号的非对角峰的强度总是相对较小，表明了其中的能量转移速率相对较慢。进一步对它们的共振能量传递信号以及非共振能量传递信号所作的定量分析表明，在越稀的溶液里所形成的离子团簇就越少，团簇的尺寸也越小。所有的结果列在表1中60,72。可以注意到，在1和1.8 mol·L－1的水溶液中，一个离子团簇内将仅包含有三到四个阴离子。因此在这些溶液中所测量得到的离子平均间距rDA可近似看作为一个离子团簇内相邻两个阴离子间的距离。根据表1中的结果，在这两种溶液中的离子间距分别为0.43和0.44 nm，比较接近于KSCN晶体中相邻两个离子的间距0.40 nm。对水溶液中离子团簇性质的进一步了解可以参考相关文献60,65－67,71,72。

5 结论与展望

综上所述，超快多维振动光谱技术，可以通过测量分子内各个振动模式跃迁偶极矩间的相对取向来获得分子体系的三维空间结构信息，以及通过振动能量转移过程测量分子之间的距离。飞秒量级的时间分辨本领，以及极其广泛的适用体系，使得此技术可有效地避免传统测量方法的一些不足，并有希望成为新一代解析分子体系三维空间构型的有力手段。但在此之前，仍然还有一些问题尚待解决。例如测量分子体系的三维空间构型时，目前所解析的大多是小的分子结构，如何将此方法扩展到生物大分子的测量将是在今后急需解决的一个问题。以解析蛋白分子的空间构型为例，一个可行的方法便是通过采用同位素标记，逐步测量蛋白分子的各个局部结构，最终构造出整个蛋白分子的空间构型。这种方案的可行性也已经得到一定的验证143。而在实际的科学问题中，我们往往仅需关注蛋白质的某些特定功能性基团的结构变化或某些基团间的相互作用，所以此方法在实际运用中还可以得到进一步的简化。由于分子的结构变化与很多生物现象以及化学反应息息相关，此技术将会在今后很多重要的科学问题中有着广泛的应用前景。

而对于利用振动能量转移过程测量分子之间距离的这种方法，在实际应用中也同样可能受到一定的制约。一方面，对于我们通常测量范围内的振动模式(频率大于800 cm－1)，其激发态在分子内的振动弛豫速度(约几个皮秒)往往都远快于分子间的振动能量转移过程(几十至几百个皮秒)。而且它们的跃迁偶极矩大小通常也远小于上述所测量C≡N键，从而使得分子间的振动能量转移信号通常会小到难于观测；另一方面，在利用各向异性信号的衰减过程测量共振能量转移速率时，往往会受到分子自身转动的影响。若分子转动的速率相当于甚至快于能量转移的速度时，将很难在信号中区分二者的贡献；此外，目前对于分子间振动能量转移机理的了解尚不够深入。尤其是在某些条件下，当非退相位机制起主要作用时，如何将实验测到的振动能量转移速率与分子之间的距离定量地连接起来，也将会是今后的一个研究重点。总之，相信随着激光技术以及探测技术的不断发展，人们将会探测到更普遍的振动能量转移过程。结合对振动能量转移机理的深入研究，将会使多维振动光谱技术应用到更多分子体系内分子间距的测量。

最后，如果把光频率推广到高达紫外可见近红外低达远红外太赫兹并结合显微技术，多维光谱技术将获得更加广泛的应用。不仅分子体系的结构与变迁，而且各种材料的微观性质及变化，如电声耦合144，二维材料层间电荷传递145，均有它的用武之地。

(1)Cahoon,J.F.;Sawyer,K.R.;Schlegel,J.P.;Harris,C.B. Science 2008,319,1820.doi:10.1126/science.1154041

(2)Kolano,C.;Helbing,J.;Kozinski,M.;Sander,W.;Hamm,P. Nature 2006,444,469.doi:10.1038/nature05352

(3)Bredenbeck,J.;Helbing,J.;Hamm,P.J.Am.Chem.Soc.2004, 126,990.doi:10.1021/ja0380190

(4)Hamm,P.;Lim,M.;Degrado,W.F.;Hochstrasser,R.M. J.Chem.Phys.2000,112,1907.doi:10.1063/1.480772

(5)Bredenbeck,J.;Ghosh,A.;Smits,M.;Bonn,M.J.Am.Chem. Soc.2008,130,2152.doi:10.1021/ja710099c5

(6)Asbury,J.B.;Steinel,T.;Stromberg,C.;Gaffney,K.J.;Piletic, I.R.;Goun,A.;Fayer,M.D.Phys.Rev.Lett.2003,91, 237402.doi:10.1103/PhysRevLett.91.2374026.

(7)Zheng,J.;Kwak,K.;Fayer,M.D.Acc.Chem.Res.2007,40, 75.doi:10.1021/ar068010d

(8)Shim,S.H.;Strasfeld,D.B.;Ling,Y.L.;Zanni,M.T.Proc. Natl.Acad.Sci.U.S.A.2007,104,14197.doi:10.1073/ pnas.0700804104

(9)Khalil,M.;Demirdoven,N.;Tokmakoff,A.J.Phys.Chem.A 2003,107,5258.doi:10.1021/jp0219247

(10)Asplund,M.C.;Zanni,M.T.;Hochstrasser,R.M.Proc.Natl. Acad.Sci.U.S.A.2000,97,8219.doi:10.1073/ pnas.140227997

(11)Tanimura,Y.;Mukamel,S.J.Chem.Phys.1993,99,9496. doi:10.1063/1.465484

(12)Mukamel,S.Principles of Nonlinear Optical Spectroscopy; Oxford University Press:New York,1995.

(13)Khalil,M.;Demirdoven,N.;Tokmakoff,A.Phys.Rev.Lett. 2003,90,047401(4).doi:10.1103/PhysRevLett.90.047401

(14)Golonzka,O.;Khalil,M.;Demirdoven,N.;Tokmakoff,A. Phys.Rev.Lett.2001,86,2154.doi:10.1103/ PhysRevLett.86.2154

(15)Rubtsov,I.V.;Kumar,K.;Hochstrasser,R.M.Chem.Phys. Lett.2005,402,439.doi:10.1016/j.cplett.2004.12.08315

(16)Zanni,M.T.;Gnanakaran,S.;Stenger,J.;Hochstrasser,R.M. J.Phys.Chem.B 2001,105,6520.doi:10.1021/jp0100093

(17)Cervetto,V.;Helbing,J.;Bredenbeck,J.;Hamm,P.J.Chem. Phys.2004,121,5935.doi:10.1063/1.1778163

(18)Sanda,F.;Mukamel,S.J.Chem.Phys.2006,125,014507. doi:10.1063/1.2205367

(19)Wang,J.P.;Chen,J.X.;Hochstrasser,R.M.J.Phys.Chem.B 2006,110,7545.doi:10.1021/jp057564f

(20)Maekawa,H.;Formaggio,F.;Toniolo,C.;Ge,N.H.J.Am. Chem.Soc.2008,130,6556.doi:10.1021/ja8007165

(21)Mukherjee,P.;Kass,I.;Arkin,I.;Zanni,M.T.Proc.Natl. Acad.Sci.U.S.A.2006,103,3528.doi:10.1073/ pnas.0508833103

(22)Maekawa,H.;Toniolo,C.;Moretto,A.;Broxterman,Q.B.; Ge,N.H.J.Phys.Chem.B 2006,110,5834.doi:10.1021/ jp057472q

(23)Baiz,C.R.;Nee,M.J.;McCanne,R.;Kubarych,K.J.Opt. Lett.2008,33,2533.doi:10.1364/OL.33.002533

(24)Zheng,J.;Kwac,K.;Xie,J.;Fayer,M.D.Science 2006,313, 1951.doi:10.1126/science.1132178

(25)Zheng,J.R.;Fayer,M.D.J.Am.Chem.Soc.2007,129,4328. doi:10.1021/ja067760f

(26)Zheng,J.;Kwak,K.;Asbury,J.B.;Chen,X.;Piletic,I.;Fayer, M.D.Science 2005,309,1338.doi:10.1126/science.1116213

(27)Zhao,W.;Wright,J.C.Phys.Rev.Lett.2000,84,1411. doi:10.1103/PhysRevLett.84.1411

(28)Wright,J.C.Int.Rev.Phys.Chem.2002,21,185.doi:10.1080/ 01442350210124506

(29)Pakoulev,A.V.;Rickard,M.A.;Meyer,K.A.;Kornau,K.; Mathew,N.A.;Thompson,D.E.;Wright,J.C.J.Phys.Chem. A 2006,110,3352.doi:10.1021/jp057339y

(30)Moilanen,D.E.;Wong,D.;Rosenfeld,D.E.;Fenn,E.E.; Fayer,M.D.Proc.Natl.Acad.Sci.U.S.A.2009,106,375. doi:10.1073/pnas.0811489106

(31)Asbury,J.B.;Steinel,T.;Stromberg,C.;Corcelli,S.A.; Lawrence,C.P.;Skinner,J.L.;Fayer,M.D.J.Phys.Chem.A 2004,108,1107.doi:10.1021/jp036266k

(32)Steinel,T.;Asbury,J.B.;Corcelli,S.A.;Lawrence,C.P.; Skinner,J.L.;Fayer,M.D.Chem.Phys.Lett.2004,386,295. doi:10.1016/j.cplett.2004.01.042

(33)Loparo,J.J.;Roberts,S.T.;Nicodemus,R.A.;Tokmakoff,A. Chem.Phys.2007,341,218.doi:10.1016/j. chemphys.2007.06.056

(34)Loparo,J.J.;Roberts,S.T.;Tokmakoff,A.J.Chem.Phys. 2006,125,194522.doi:10.1063/1.2382896

(35)Fecko,C.J.;Eaves,J.D.;Loparo,J.J.;Tokmakoff,A.; Geissler,P.L.Science 2003,301,1698.doi:10.1126/ science.1087251

(36)Cowan,M.L.;Bruner,B.D.;Huse,N.;Dwyer,J.R.;Chugh, B.;Nibbering,E.T.J.;Elsaesser,T.;Miller,R.J.D.Nature 2005,434,199.doi:10.1038/nature03383

(37)Cervetto,V.;Hamm,P.;Helbing,J.J.Phys.Chem.B 2008, 112,8398.doi:10.1021/jp801166q

(38)Kozinski,M.;Garrett-Roe,S.;Hamm,P.J.Phys.Chem.B 2008,112,7645.doi:10.1021/jp8005734

(39)Finkelstein,I.J.;Zheng,J.R.;Ishikawa,H.;Kim,S.;Kwak, K.;Fayer,M.D.Phys.Chem.Chem.Phys.2007,9,1533. doi:10.1039/B618158A

(40)Finkelstein,I.J.;Ishikawa,H.;Kim,S.;Massari,A.M.;Fayer, M.D.Proc.Natl.Acad.Sci.U.S.A.2007,104,2637. doi:10.1073/pnas.0610027104

(41)Treuffet,J.;Kubarych,K.J.;Lambry,J.C.;Pilet,E.;Masson, J.B.;Martin,J.L.;Vos,M.H.;Joffre,M.;Alexandrou,A. Proc.Natl.Acad.Sci.U.S.A.2007,104,15705.doi:10.1073/ pnas.0703279104

(42)Ishikawa,H.;Kwak,K.;Chung,J.K.;Kim,S.;Fayer,M.D. Proc.Natl.Acad.Sci.U.S.A.2008,105,8619.doi:10.1073/ pnas.0803764105

(43)Ganim,Z.;Chung,H.S.;Smith,A.W.;Deflores,L.P.;Jones, K.C.;Tokmakoff,A.Acc.Chem.Res.2008,41,432. doi:10.1021/ar700188n

(44)DeCamp,M.F.;DeFlores,L.;McCracken,J.M.;Tokmakoff, A.;Kwac,K.;Cho,M.J.Phys.Chem.B 2005,109,11016. doi:10.1021/jp050257p

(45)Fang,C.;Bauman,J.D.;Das,K.;Remorino,A.;Arnold,E.; Hochstrasser,R.M.Proc.Natl.Acad.Sci.U.S.A.2008,105, 1472.doi:10.1073/pnas.0709320104

(46)Mukherjee,P.;Kass,I.;Arkin,I.T.;Zanni,M.T.J.Phys. Chem.B 2006,110,24740.doi:10.1021/jp0640530

(47)Woutersen,S.;Mu,Y.;Stock,G.;Hamm,P.Chem.Phys.2001, 266,137.doi:10.1016/S0301-0104(01)00224-5

(48)Kim,Y.S.;Hochstrasser,R.M.Proc.Natl.Acad.Sci.U.S.A. 2005,102,11185.doi:10.1073/pnas.0504865102

(49)Zheng,J.;Kwak,K.;Chen,X.;Asbury,J.B.;Fayer,M.D. J.Am.Chem.Soc.2006,128,2977.doi:10.1021/ja0570584

(50)Zheng,J.;Fayer,M.D.J.Phys.Chem.B 2008,112,10221. doi:10.1021/jp804087v

(51)Khalil,M.;Demirdoven,N.;Tokmakoff,A.J.Chem.Phys. 2004,121,362.doi:10.1063/1.1756870

(52)Zheng,J.;Kwak,K.;Steinel,T.;Asbury,J.B.;Chen,X.;Xie, J.;Fayer,M.D.J.Chem.Phys.2005,123,164301. doi:10.1063/1.2071967

(53)Naraharisetty,S.R.G.;Kasyanenko,V.M.;Rubtsov,I.V. J.Chem.Phys.2008,128,104502.doi:10.1063/1.2842071

(54)Naraharisetty,S.R.G.;Kurochkin,D.V.;Rubtsov,I.V.Chem. Phys.Lett.2007,437,262.doi:10.1016/j.cplett.2007.02.020

(55)Nee,M.J.;Baiz,C.R.;Anna,J.M.;McCanne,R.;Kubarych, K.J.J.Chem.Phys.2008,129,084503.doi:10.1063/ 1.2969900

(56)Barbour,L.W.;Hegadorn,M.;Asbury,J.B.J.Am.Chem.Soc. 2007,129,15884.doi:10.1021/ja074657x

(57)Barbour,L.W.;Hegadorn,M.;Asbury,J.B.J.Phys.Chem.B 2006,110,24281.doi:10.1021/jp065639p

(58)Chen,H.;Zhang,Q.;Guo,X.;Wen,X.;Li,J.;Zhuang,W.; Zheng,J.J.Phys.Chem.A 2015,119,669.doi:10.1021/ jp511651t

(59)Chen,H.;Wen,X.;Li,J.;Zheng,J.J.Phys.Chem.A 2014, 118,2463.doi:10.1021/jp500586h

(60)Chen,H.;Wen,X.;Guo,X.Phys.Chem.Chem.Phys.2014, 16,13995.doi:10.1039/C4CP01300J

(61)Chen,H.;Bian,H.;Li,J.;Wen,X.;Zheng,J.Int.Rev.Phys. Chem.2012,31,469.doi:10.1080/0144235X.2012.733116

(62)Chen,H.;Bian,H.;Li,J.;Wen,X.;Zheng,J.J.Phys.Chem.A 2013,117,6052.doi:10.1021/jp312604v

(63)Chen,H.;Bian,H.;Li,J.;Guo,X.;Wen,X.;Zheng,J.J.Phys. Chem.B 2013,117,15614.doi:10.1021/jp406232k

(64)Chen,H.;Zhang,Y.;Li,J.;Liu,H.;Jiang,D.E.;Zheng,J. J.Phys.Chem.A 2013,117,8407.doi:10.1021/jp406304c

(65)Chen,H.;Bian,H.;Li,J.;Wen,X.;Zhang,Q.;Zhuang,W.; Zheng,J.J.Phys.Chem.B 2015,119,4333.doi:10.1021/ jp512320a

(66)Bian,H.;Chen,H.;Li,J.;Wen,X.;Zheng,J.J.Phys.Chem.A 2011,115,11657.doi:10.1021/jp206937u

(67)Bian,H.;Chen,H.;Zhang,Q.;Li,J.;Wen,X.;Zhuang,W.; Zheng,J.J.Phys.Chem.B 2013,117,7972.doi:10.1021/ jp4016646

(68)Bian,H.;Li,J.;Chen,H.;Yuan,K.;Wen,X.;Li,Y.;Sun,Z.; Zheng,J.J.Phys.Chem.C 2012,116,7913.doi:10.1021/ jp300970p

(69)Bian,H.;Li,J.;Wen,X.;Sun,Z.;Song,J.;Zhuang,W.;Zheng, J.J.Phys.Chem.A 2011,115,3357.doi:10.1021/jp200516p

(70)Bian,H.;Li,J.;Wen,X.;Zheng,J.R.J.Chem.Phys.2010, 132,184505.doi:10.1063/1.3429170

(71)Bian,H.;Li,J.;Zhang,Q.;Chen,H.;Zhuang,W.;Gao,Y.Q.; Zheng,J.J.Phys.Chem.B 2012,116,14426.doi:10.1021/ jp310153n

(72)Bian,H.;Wen,X.;Li,J.;Chen,H.;Han,S.;Sun,X.;Song,J.; Zhuang,W.;Zheng,J.Proc.Nat.Acad.Sci.U.S.A.2011,108, 4737.doi:10.1073/pnas.1019565108

(73)Li,J.;Bian,H.;Chen,H.;Wen,X.;Hoang,B.;Zheng,J. J.Phys.Chem.B 2012,117,4274.doi:10.1021/jp3053373

(74)Li,J.;Bian,H.;Wen,X.;Chen,H.;Yuan,K.;Zheng,J. J.Phys.Chem.B 2012,116,12284.doi:10.1021/jp306369w

(75)Shen,Y.;Wu,T.;Jiang,B.;Deng,G.;Li,J.;Chen,H.;Guo,X.; Ge,C.;Chen,Y.;Hong,J.J.Phys.Chem.B 2015,119,9893. doi:10.1021/acs.jpcb.5b04530

(76)Tian,P.;Keusters,D.;Suzaki,Y.;Warren,W.S.Science 2003, 300,1553.doi:10.1126/science.1083433

(77)DeFlores,L.P.;Ganim,Z.;Nicodemus,R.A.;Tokmakoff,A. J.Am.Chem.Soc.2009,131,3385.doi:10.1021/ja8094922

(78)Haleblian,J.;McCrone,W.J.Pharm.Sci.1969,58,911. doi:10.1002/jps.2600580802

(79)Haleblian,J.K.J.Pharm.Sci.1975,64,1269.doi:10.1002/ jps.2600640805

(80)Borka,L.;Haleblian,J.K.Acta Pharm.Jugosl.1990,40,71.

(81)Weissenhorn,W.;Dessen,A.;Calder,L.;Harrison,S.;Skehel, J.;Wiley,D.Mol.Membr.Biol 1999,16,3.doi:10.1080/ 096876899294706

(82)Gibbons,D.L.;Vaney,M.C.;Roussel,A.;Vigouroux,A.; Reilly,B.;Lepault,J.;Kielian,M.;Rey,F.A.Nature 2004, 427,320.doi:10.1038/nature02239

(83)Ernst,R.R.;Bodenhausen,G.;Wokaun,A.Nuclear Magnetic Resonance in One and Two Dimensions;Oxford University Press:Oxford,U.K.,1987.

(84)Bifulco,G.;Dambruoso,P.;Gomez-Paloma,L.;Riccio,R. Chem.Rev.2007,107,3744.doi:10.1021/cr030733c

(85)DeFlores,L.P.;Nicodemus,R.A.;Tokmakoff,A.Opt.Lett. 2007,32,2966.doi:10.1364/OL.32.002966

(86)Shim,S.H.;Strasfeld,D.B.;Zanni,M.T.Opt.Express.2006, 14,13120.doi:10.1364/OE.14.013120

(87)Shim,S.H.;Strasfeld,D.B.;Fulmer,E.C.;Zanni,M.T.Opt. Lett.2006,31,838.doi:10.1364/OL.31.000838

(88)Shim,S.H.;Zanni,M.T.Phys.Chem.Chem.Phys.2009,11, 748.doi:10.1039/B813817F

(89)Xiong,W.;Zanni,M.T.Opt.Lett.2008,33,1371. doi:10.1364/OL.33.001371

(90)Zheng,J.Ultrafast Chemical Exchange Spectroscopy;VDM Verlag:Saarbrücken,Germany,2008.

(91)Asbury,J.B.;Steinel,T.;Fayer,M.D.J.Lumin.2004,107, 271.doi:10.1016/j.jlumin.2003.12.035

(92)Calabrese,C.;Stingel,A.M.;Shen,L.;Petersen,P.B.Opt. Lett.2012,37,2265.doi:10.1364/OL.37.002265

(93)Petersen,P.B.;Tokmakoff,A.Opt.Lett.2010,35,1962. doi:10.1364/OL.35.001962

(94)Gattermann,L.Ber.Dtsch.Chem.Ges.1885,18,1482. doi:10.1002/cber.188501801319

(95)Moore,J.C.;Yeadon,A.;Palmer,R.A.J.Chem.Crystallogr. 1983,13,279.doi:10.1007/BF01158908

(96)Fayer,M.D.Ultrafast Infrared and Raman Spectroscopy; Marcel Dekker,Inc:New York,Basel,2001;Vol.26.

(97)Lakowicz,J.Principles of Fluorescence Spectroscopy,3rd ed.; Springer:New York,2006.

(98)Murray,C.B.;Kagan,C.R.;Bawendi,M.G.Annu.Rev. Mater.Sci.2000,30,545.doi:10.1146/annurev.matsci.30.1.545

(99)Penn,S.G.;He,L.;Natan,M.J.Curr.Opin.Chem.Biol.2003, 7,609.doi:10.1016/j.cbpa.2003.08.013

(100)Bell,A.T.Science 2003,299,1688.doi:10.1126/ science.1083671

(101)Park,S.J.;Taton,T.A.;Mirkin,C.A.Science 2002,295, 1503.doi:10.1126/science.1067003

(102)Sperling,R.A.;Rivera gil,P.;Zhang,F.;Zanella,M.;Parak, W.J.Chem.Soc.Rev.2008,37,1896.doi:10.1039/b712170a

(103)Ghosh,P.;Han,G.;De,M.;Kim,C.K.;Rotello,V.M.Adv. Drug Deliv.Rev.2008,60,1307.doi:10.1016/j. addr.2008.03.016

(104)Huang,X.H.;Jain,P.K.;El-Sayed,I.H.;El-Sayed,M.A. Nanomedicine 2007,2,681.doi:10.2217/17435889.2.5.681

(105)Maxwell,D.J.;Taylor,J.R.;Nie,S.M.J.Am.Chem.Soc. 2002,124,9606.doi:10.1021/ja025814p

(106)Shukla,N.;Bartel,M.A.;Gellman,A.J.J.Am.Chem.Soc. 2010,132,8575.doi:10.1021/ja908219h

(107)Pissuwan,D.;Valenzuela,S.M.;Cortie,M.B.Trends Biotechnol.2006,24,62.doi:10.1016/j.tibtech.2005.12.004

(108)Jin,Q.;Rodriguez,J.A.;Li,C.Z.;Darici,Y.;Tao,N.J.Surf. Sci.1999,425,101.doi:10.1016/s0039-6028(99)00195-8

(109)Daniel,M.C.;Astruc,D.Chem.Rev.2004,104,293. doi:10.1021/cr030698+

(110)Valden,M.;Lai,X.;Goodman,D.W.Science 1998,281,1647. doi:10.1126/science.281.5383.1647

(111)Paulus,P.M.;Goossens,A.;Thiel,R.C.;van der Kraan,A.M.;Schmid,G.;de Jongh,L.J.Phys.Rev.B 2001,64,205418. doi:10.1103/PhysRevB.64.205418

(112)Nahler,N.H.;White,J.D.;Larue,J.;Auerbach,D.J.;Wodtke, A.M.Science 2008,321,1191.doi:10.1126/science.1160040

(113)Wodtke,A.M.;Matsiev,D.;Auerbach,D.J.Prog.Surf.Sci. 2008,83,167.doi:10.1016/j.progsurf.2008.02.001

(114)Andersson,S.;Pendry,J.B.Phys.Rev.Lett.1979,43,363. doi:10.1103/PhysRevLett.43.363

(115)Li,J.;Qian,H.;Chen,H.;Zhao,Z.;Yuan,K.;Chen,G.; Miranda,A.;Guo,X.;Chen,Y.;Zheng,N.Nat.Commun. 2016,7,10749.doi:10.1038/ncomms10749

(116)Van Gunsteren,W.;Berendsen,H.J.Mol.Biol.1984,176,559. doi:10.1016/0022-2836(84)90177-3

(117)Skrynnikov,N.R.;Goto,N.K.;Yang,D.;Choy,W.Y.; Tolman,J.R.;Mueller,G.A.;Kay,L.E.J.Mol.Biol.2000, 295,1265.doi:10.1006/jmbi.1999.3430

(118)Kurochkin,D.V.;Naraharisetty,S.R.G.;Rubtsov,I.V.Proc. Natl.Acad.Sci.U.S.A.2007,104,14209.doi:10.1073/ pnas.0700560104

(119)Rubtsov,I.V.Acc.Chem.Res.2009,42,1385.doi:10.1021/ ar900008p

(120)Kasyanenko,V.M.;Tesar,S.L.;Rubtsov,G.I.;Burin,A.L.; Rubtsov,I.V.J.Phys.Chem.B 2011,115,11063.doi:10.1021/ jp2066315

(121)Förster,T.Ann.Phys.1948,437,55.doi:10.1002/ andp.19484370105

(122)Scholes,G.D.Annu.Rev.Phys.Chem.2003,54,57. doi:10.1146/annurev.physchem.54.011002.103746

(123)Bian,H.T.;Wen,X.W.;Li,J.B.;Zheng,J.R.J.Chem.Phys. 2010,133,034505.doi:03450510.1063/1.3458825

(124)Hong,X.Y.;Chen,S.;Dlott,D.D.J.Phys.Chem.1995,99, 9102.doi:10.1021/j100022a023

(125)Laubereau,A.;Kirschner,L.;Kaiser,W.Opt.Commun.1973, 9,182.

(126)Laubereau,A.;Kaiser,W.Rev.Mod.Phys.1978,50,607. doi:10.1103/RevModPhys.50.607

(127)Woutersen,S.;Bakker,H.J.Nature 1999,402,507. doi:10.1038/990058

(128)Gaffney,K.J.;Piletic,I.R.;Fayer,M.D.J.Chem.Phys.2003, 118,2270.doi:10.1063/1.1534580

(129)Seifert,G.;Zurl,R.;Patzlaff,T.;Graener,H.J.Chem.Phys. 2000,112,6349.doi:10.1063/1.481195

(130)Förster,T.Ann.Phys.Leipzig 1948,2,55.

(131)Petersen,K.A.;Fayer,M.D.J.Chem.Phys.1986,85,4702. doi:10.1063/1.451745

(132)Oxtoby,D.W.Adv.Chem.Phys.1981,47,487.

(133)Knox,R.S.;vanAmerongen,H.J.Phys.Chem.B 2002,106, 5289.doi:10.1021/jp013927+

(134)Skinner,J.Theor.Chem.Acc.2011,128,147.doi:10.1007/ s00214-010-0834-3

(135)Nitzan,A.;Mukamel,S.;Jortner,J.J.Chem.Phys.1975,63, 200.doi:

(136)Rackovsky,S.;Silbey,R.Mol.Phys.1973,25,61. doi:10.1063/1.431045

(137)Leegwater,J.A.J.Phys.Chem.1996,100,14403. doi:10.1021/jp961448i

(138)Fayer,M.D.Elements of Quantum Mechanics;Oxford University Press:New York,2001.

(139)Kenkre,V.M.;Tokmakoff,A.;Fayer,M.D.J.Chem.Phys. 1994,101,10618.doi:10.1063/1.467876

(140)Egorov,S.;Skinner,J.J.Chem.Phys.1995,103,1533. doi:10.1063/1.469775

(141)Holstein,T.;Lyo,S.;Orbach,R.Excitation Transfer in Disordered Systems.In Laser Spectroscopy of Solids;Springer: New York,1986;pp 39－82.

(142)Dlott,D.D.Chem.Phys.2001,266,149.doi:10.1016/S0301-0104(01)00225-7

(143)Remorino,A.;Korendovych,I.V.;Wu,Y.;DeGrado,W.F.; Hochstrasser,R.M.Science 2011,332,1206.doi:10.1126/ science.1202997

(144)Guo,X.;Chen,H.;Wen,X.;Zheng,J.J.Chem.Phys.2015, 142,212447.doi:10.1063/1.4921573

(145)Chen,H.;Wen,X.;Zhang,J.;Wu,T.;Gong,Y.;Zhang,X.; Yuan,J.;Yi,C.;Lou,J.;Ajayan,P.M.;Zhang,G.;Zhuang,W.; Zheng,J.Nat.Commun.2016,7,12512.doi:10.1038/ ncomms12512

Determining 3D Molecular Conformations with Ultrafast Multiple-Dimensional Vibrational Spectroscopy

CHEN Hai-Long2BIAN Hong-Tao3ZHENG Jun-Rong1,*
(1Beijing National Laboratory for Molecular Sciences,College of Chemistry and Molecular Engineering,Peking University, Beijing 100871,P.R.China;2Beijing National Laboratory for Condensed Matter Physics and CAS Key Laboratory of Soft Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,P.R.China;3School of Chemistry and Chemical Engineering,Shaanxi Normal University,Xi′an 710119,P.R.China)

In recent years,ultrafast multiple-dimensional vibrational spectroscopy has been widely applied to studies of molecular structures and ultrafast dynamics in various condensed phases,and is expected to become a new generation of routine analytical tool for determining microstructures and ultrafast behaviors in molecular systems.In this review,we introduce in detail a method of determining three-dimensional(3D) molecular conformations with ultrafast multiple-dimensional vibrational spectroscopy.The introduction of our research follows two directions:(1)obtaining relative spatial orientations of different groups in a molecular system and finally determining molecular conformations by measuring cross angles of vibrational transition dipole moments;and(2)exploring the nature of vibrational energy transfers and determining molecular distances with experimentally measured vibrational energy transfer rates.

Multiple-dimensional vibrational spectroscopy;Ultrafast spectroscopy;2D infrared spectroscopy;Molecular conformation;Vibrational energy transfer

O649

iew]

10.3866/PKU.WHXB201609192www.whxb.pku.edu.cn

Received:July 22,2016;Revised:September 16,2016;Published online:September 19,2016.

*Corresponding author.Email:junrong@pku.edu.cn;Tel:+86-10-62753815.

The project was supported by theAFOSR YIPAward,USA(FA9550-11-1-0070)and anAFOSR MURI grant,USA(FA9550-15-1-0022),the Welch

Foundation,USA(C-1752),NSF USA(CHE-1503865),ACS PRF,USA,Packard fellowship,USA,and Sloan fellowship,USA.

美国空军科学研究局青年学者奖(FA9550-11-1-0070),美国空军科学研究局多学科大学研究创新基金(FA9550-15-1-0022),美国韦尔奇基金(C-1752),美国国家科学基金(CHE-1503865),美国化学学会石油研究基金及美国帕卡德奖和美国斯隆奖资助