基于压缩感知的进动目标ISAR成像方法

刘记红， 徐少坤， 韩国强， 魏雁飞

(中国洛阳电子装备试验中心， 河南洛阳 471003)

0 引言

弹道目标识别是导弹攻防对抗胜负的关键环节。逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)成像能够反映目标的尺寸、结构、形状等特征[1]，在雷达目标识别领域发挥着极其重要的作用，已成为弹道目标识别的主要途径之一。对于弹道目标而言，除高速轨道运动外，通常还伴随有自旋、进动等复杂的运动形式，大大增加了ISAR成像的难度。进动是弹道中段弹头目标的重要物理特性之一，它使得目标姿态角呈现近似正弦规律的非均匀变化，目标上各散射点在距离上出现类似正弦曲线的距离走动，导致相应的ISAR成像问题较为复杂，常规成像算法难以获得高质量的ISAR图像[2]。

弹道目标成像问题是ISAR成像领域的研究热点，由于军事敏感性，国外相关的研究成果很少见诸报道，但可从零星的报道中获知某些导弹防御雷达具备了弹头ISAR成像能力。国内的研究起步较晚，直到近些年才有少量的文献出现。目前，用于进动目标的成像方法主要有基于时频变换的方法[3-5]、基于复数逆投影的方法[6]、基于宽带复数后向投影变换(Back Projection Transform, BPT)的方法[2]等。上述方法在一定条件下能够获得较好的成像结果，但对回波数据要求较高，成像性能敏感于目标的进动参数，而在实际应用过程中，获取的数据段或目标进动参数往往难以满足要求，如弹道目标的高速运动、反导系统雷达对多目标的跟踪需求、导弹突防中的电子干扰措施等因素都可能导致无法获得充足的观测数据，需要进一步研究利用有限脉冲回波数据进行弹道目标ISAR成像的方法。

近年来，压缩感知(Compressed Sensing, CS)理论在高分辨雷达成像领域受到了越来越多的关注[7-9]，其利用较少的测量数据即可重构出雷达目标图像的特性，为进一步完善传统雷达成像技术提供了契机，也为弹道中段进动目标成像提供了一种新思路。文献[10]将CS理论引入到目标微动特性分析中，获取了目标回波的微多普勒时频谱；文献[11]研究了CS理论在含旋转部件目标成像中的应用，获取该类目标主体部分的ISAR图像。本文针对弹道中段进动目标的ISAR成像问题，在分析旋转对称进动目标回波模型的基础上，充分利用雷达目标散射率分布的稀疏性先验信息和目标的进动信息，提出了基于CS的进动目标成像算法，在降低脉冲重复频率(Pulse Repetition Frequency, PRF)实际需求的同时，实现了进动目标的高分辨成像。

1 弹道中段进动目标回波模型

进动是一种自旋加锥旋的复合运动形式，弹道中段进动目标的运动模型如图1所示，其中3个坐标系的建立方式同文献[2]，O为目标质心，ωs,ωc分别为自旋和进动角频率，目标进动轴ON在YOZ平面内，俯仰角为βN。假设初始时刻目标自旋轴(z轴)也位于YOZ平面内，Z轴与z轴之间的夹角为θ，则目标的进动角为γ=π/2-θ-βN。

图1 雷达与空间进动目标几何关系示意图

弹道中段目标的形体结构比较简单，除少部分战术弹道导弹外，弹头及诱饵大都是旋转对称体。文献[2]的分析表明，对于旋转对称体目标而言，自旋不会带来散射场的变化，目标的三维姿态运动可以等效为在二维成像平面内的旋转，转动规律对应目标的姿态角变化规律。将目标在三维空间的旋转运动等效为在二维成像平面内目标对称轴绕点O的转动，则等效旋转角，即目标的姿态角为

α(t)=arc cos(cosγsinβN+sinγcosβNcosωct)

(1)

由于进动角较小，通常为5°～15°，对应α(t)的变化范围较小，可用直线方程近似，即

α(t)≈arc cos(sinβN+γcosβNcosωct)≈

(2)

式中，θc=π/2-βN为雷达观测目标的平均视线角，它随目标的轨道运动而变化，相对于微动带来的姿态变化，θc的变化比较缓慢。

当将目标的进动等效为二维平面内的转动时，目标的等效散射中心模型也可等效到二维平面内。设等效成像平面为Z′OY′，则在Z′OY′平面内以α(t)为规律转动的目标回波与进动状态下的旋转对称目标回波等效。假设雷达发射线性调频信号，目标共包含I个散射点，等效成像平面内目标上第i个散射点的坐标为(zi,yi)，散射强度为δi，则消除了平动影响的雷达目标回波可表示为

ΔRi(tm)=zicosα(tm)+yisinα(tm)

(4)

根据前述分析，目标的姿态角主要取决于其进动参数，目前关于进动参数的估计算法有很多[12]，若已经得到目标的平均视线角和进动参数，则可获得目标的姿态角变化规律，进而基于式(5)重构目标的二维图像。由式(2)可知，进动使得中段目标的成像面临如下问题： 1) 进动使得方位向的采样间隔呈类正弦规律变化，期间目标姿态角在两倍的进动角范围内非均匀变化，且不能用匀加速转动模型进行等效； 2) 与高速自旋目标不同，由于进动角一般较小，进动过程中目标的姿态角变化范围不大，基于窄带信息的自旋目标成像方法[13]不适用于进动目标。

2 基于压缩感知的进动目标成像

鉴于CS利用少量测量数据即可实现高分辨雷达成像的特点，这里将CS引入到旋转对称进动目标的ISAR成像中，其原理是基于目标回波信号的稀疏性，利用少量非相干测量通过非线性优化重构雷达目标图像。

2.1 回波模型的线性化表征

雷达回波的稀疏性表征和模型的线性化处理是CS成像的先决条件。将成像区间离散化为P×Q的二维网格，每个网格点代表可能存在散射点的位置坐标(zp,yq)，相应位置处的散射强度表示为δpq(p=0,1,…,P-1,q=0,1,…,Q-1)。离散间隔大小决定了重构图像的分辨率，当某一个网格交点的坐标(zp,yq)上存在等效散射中心时，此网格点上的散射强度δpq≠0；反之，δpq=0。由于目标所涵盖的仅是一部分网格交点，且目标仅包含有限个等效散射中心，PQ个网格交点中绝大多数位置上都不存在散射中心，因此目标散射率分布具有很强的稀疏性。

假设距离向的采样点数为N(N≤P)，对应的基频采样点为fn(n=0,1,…,N-1)，方位向用于成像的脉冲数为M(M≤Q)，则根据式(5)可构造进动目标的观测矩阵如下：

Φ=[Φ(0),Φ(1),…,Φ(M-1)]

(6)

设Y为测得的N×M维的回波数据矩阵，δ=[δpq]P×Q为目标的二维散射率分布矩阵，按列堆叠后的矢量化表示形式分别为y=vec(Y)和σ=vec(δ)，则式(5)可表示为如下矩阵形式：

y=Φσ

(7)

2.2 雷达图像形成

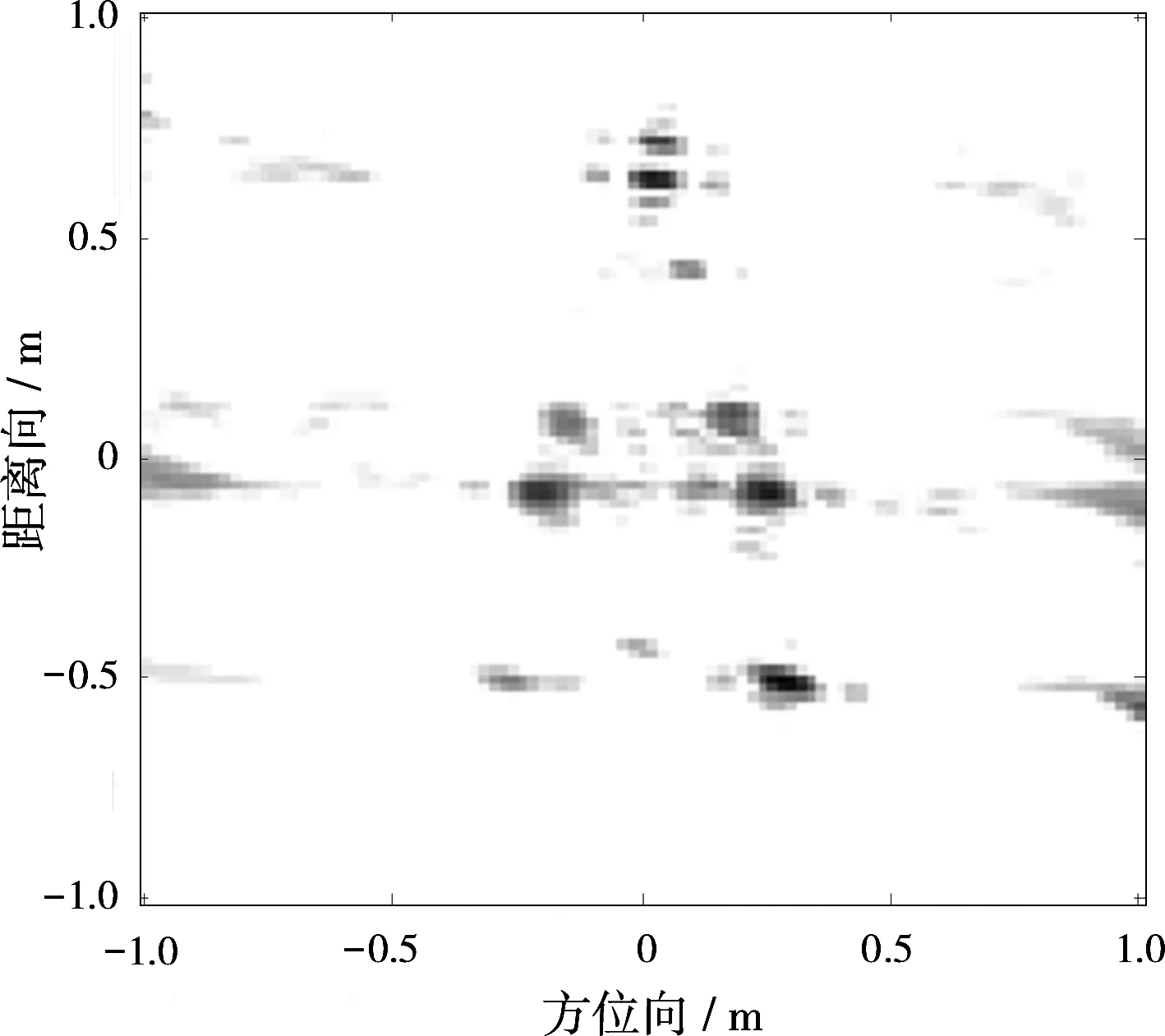
根据CS理论，当式(7)中的Φ满足一定条件[8]时，通过非线性优化即可重构σ，进而通过重排得到目标的二维图像。该方法的优势在于，能够克服方位向非均匀采样的影响，保证角度变化范围较小情况下的成像分辨率，且当PRF不满足Nyquist采样准则而使回波产生欠采样时依然有效。值得注意的是，此时测量矩阵Φ的维数较高(MN×PQ)，将在计算中占据大量的存储空间，而且大矩阵的乘法和求逆运算计算量较大，使得算法整体复杂度较高。事实上， CS重构过程中无需采用所有的回波数据，可对雷达回波进行降采样处理。假设距离向随机采样K点，方位向获得的脉冲回波数为L(K

上述方法通过CS算法实现了进动目标雷达图像的二维联合重构，所需的存储量和计算量较大。根据观测矩阵元素的构造过程可知，目标散射率在方位向和距离向的分布均与目标姿态角(慢时间)耦合在一起，无法得到观测模型的解耦形式，不能通过距离向和方位向分别重构的方式降低算法的复杂度。为进一步降低所提成像算法的存储需求，可利用每个测量频点的信息分别进行重构，然后对各个频点的重构结果进行相干叠加，进而通过重排得到目标的高分辨ISAR图像，这里称之为“分频处理方法”。

yn=Φnσ

(8)

通过CS算法求解式(8)可得到第n个测量频点处的重构结果，对各个频点数据执行相同的操作，然后叠加合成重构结果，即可得到清晰的目标ISAR图像。

3 算法性能分析

从理论上讲，所提基于CS的进动目标成像算法充分利用了雷达目标散射率分布的稀疏性先验信息和目标的进动信息，通过少量回波数据即可实现进动目标的高分辨成像，有效降低了进动目标成像所需的PRF，提高了数据利用率，付出的代价是重构过程复杂度的增加。从成像质量上来看，二维数据联合处理的重构模型与雷达观测模型较匹配，性能相对稳定，能获得较理想的成像结果；分频处理方法将各个频点测量数据分别处理，忽略了各频点回波数据间的耦合效应，在相同测量条件下图像质量将有所损失。

从资源需求和运算复杂度上看，以运算效率较高的SL0算法[14]为例，二维联合成像算法需要的总存储量为O(KLPQ)，每次迭代运行时间为O(KLPQ)，总的计算复杂度为O(JL0KLPQ)，其中J=O(1),L0=O(1)分别表示外层和内层循环次数；分频处理方法需要的存储量为O(LPQ)，每个频点每次迭代重构的时间复杂度为O(LPQ)，共计重复K次，故总的运行时间为O(JL0KLPQ)，与二维联合成像算法在一个量级上。可见，在同等测量条件下，二者的运算开销大致相同，但二维联合处理方式需要更多的存储空间。实际中，弹道中段进动目标的形体较小且结构简单，上述两种成像处理方法均是可行的。

4 仿真实验及分析

实验中利用仿真数据和暗室合成数据验证了所提成像算法的有效性，由于篇幅限制，这里仅给出暗室数据结果。暗室测量目标的外形尺寸如图2所示，测量扫频范围为8～12GHz，扫频间隔20MHz，目标姿态为俯仰角0°，方位角0°～90°变化(鼻翼方向为0°)，变化间隔为0.2°。选用8～12GHz频段和相应姿态下的测量数据合成进动目标的回波，从而验证所提CS成像算法的性能，CS方法重构过程中采用SL0算法。合成参数设置如下：目标起始姿态角为0°，进动周期为1s，雷达信号带宽B=4 GHz，测量频点数N=201，PRF为500 Hz，先后合成进动角为5°和10°时的目标回波，成像过程中采用一个进动周期内的回波数据。

图2 暗室测量目标外形尺寸图

图3给出了进动角为10°时合成进动目标回波的距离压缩结果和常规距离-多普勒(Range-Doppler, RD)算法成像结果。可见，进动目标的距离-慢时间域回波具有一定的周期性，合成数据反映了进动目标的姿态变化规律，常规的RD算法无法获得清晰的ISAR图像。

(b)RD成像结果图3 暗室合成进动目标距离-慢时间域回波及RD成像结果

为验证所提CS成像方法的有效性，并与现有的BPT方法进行比较，对目标进动角γ=5°，10°的情况，分别先后采用BPT方法、二维数据联合处理的CS方法和分频处理的CS方法进行成像，结果如图4、图5所示。其中，图示结果的动态范围取为30 dB，为便于存储和计算， CS方法重构过程中对回波数据进行了降采样，距离向随机采样31个频点，方位向进行19倍的均匀降采样，分频处理方式未对距离向进行降采样。

(a)γ=5°

(b)γ=10°图4基于BPT的进动目标成像结果

(a)二维联合处理(γ=5°)

(b)二维联合处理(γ=10°)

(c)分频处理(γ=5°)

(d)分频处理(γ=10°)图5基于CS的进动目标成像结果

从重构结果可以看出， BPT方法和CS方法均能够有效地对进动目标成像。相比之下，BPT方法的成像结果具有较高的旁瓣和较多的背景杂波，且对进动角大小较为敏感；CS方法特别是二维联合处理的成像结果清晰地反映了目标的散射点分布，具有较好的旁瓣抑制能力，成像性能受进动角大小的影响较小，且适用于获得数据十分有限的情况；分频处理的CS成像质量略低于二维联合处理方法，这是因为它割裂了各采样频点数据间的相关性，与理论分析一致。

为分析带宽对成像性能的影响，图6给出了合成回波数据带宽为2 GHz(9～11 GHz)、目标进动角为10°情况下的成像结果。可以看出， BPT方法的成像性能受带宽影响较大，这是由于它在重构过程中利用的是目标的一维距离像信息，受sinc函数主瓣宽度的影响，带宽越小影响越大。相比之下， CS方法利用的是目标的回波数据，尽管成像质量也随着带宽的降低有所下降，但仍较为准确清晰地反映了目标的二维散射率分布。

(a)BPT方法

(b)CS方法(二维联合处理)图6带宽2 GHz条件下的进动目标成像结果

此外，实验过程中发现，一味地增加CS重构所用的样本数并不一定能改善成像质量，相反可能导致成像结果的严重失真。分析原因可知，与高速自旋目标不同，由于进动角较小，进动目标的姿态角变化范围相对较小，当采样较密时，稀疏字典的原子间可能具有较高的相似性，使得重构性能对噪声非常敏感，只有在高信噪比下才能获得较好的重构结果；当采样较疏时，稀疏字典原子间的相似性较低，重构性能对噪声更为稳健。

5 结束语

以弹道中段弹头目标为代表的进动目标成像是ISAR成像研究的一个重要方面。本文在详细分析弹道中段进动目标电磁散射特性的基础上，研究了基于压缩感知的进动目标成像算法。首先提出了基于二维数据联合处理的CS成像方法，然后针对该方法重构过程中存在的存储空间需求较大的问题，提出了基于分频处理的进动目标成像方法，对两种算法的性能进行了分析比较，通过暗室合成数据验证了所提方法的有效性。与现有方法相比，所提方法不仅可以在少量数据条件下实现进动目标的高分辨成像，充分改善了成像质量，而且提高了对目标进动参数的稳定性。

[1]金胜,朱天林. ISAR高分辨率成像方法综述[J]. 雷达科学与技术, 2016, 14(3):251-260. JIN Sheng, ZHU Tianlin. A Review of High-Resolution Inverse Synthetic Aperture Radar Imaging Methods[J]. Radar Science and Technology, 2016, 14(3):251-260.(in Chinese)

[2]胡杰民. 复杂运动目标高分辨雷达成像技术研究[D]. 长沙：国防科学技术大学, 2011.

[3]DING Xiaofeng, FAN Meimei, WEI Xizhang, et al. Narrowband Imaging Method for Spatial Precession Cone-Shaped Targets[J]. Science China Technological Sciences, 2010, 53(4):942-949.

[4]WANG Tao, WANG Xuesong, CHANG Yuliang, et al. Estimation of Precession Parameters and Generation of ISAR Images of Ballistic Missile Targets[J]. IEEE Trans on Aerospace and Electronic Systems, 2010, 46(4):1983-1995.

[5]PAN Xiaoyi, WANG Wei, LIU Jin, et al. Modulation Effect and Inverse Synthetic Aperture Radar Imaging of Rotationally Symmetric Ballistic Targets with Precession[J]. IET Radar, Sonar & Navigation, 2013, 7(9):950-958.

[6]胡晓伟,童宁宁,王建业,等. 基于组网雷达的空间旋转对称进动目标三维重构[J]. 系统工程与电子技术, 2016, 38(10):2281-2286. HU Xiaowei, TONG Ningning, WANG Jianye, et al. Three-Dimensional Reconstruction for Spatial Precession Targets with Rotational Symmetry in Radar Networks[J]. Systems Engineering and Electronics, 2016, 38(10):2281-2286.(in Chinese)

[7]ZHANG Shunsheng, Zhang Wei, ZONG Zhulin, et al. High-Resolution Bistatic ISAR Imaging Based on Two-Dimensional Compressed Sensing[J]. IEEE Trans on Antennas and Propagation, 2015, 63(5):2098-2111.

[8]李少东,杨军,陈文峰,等. 基于压缩感知理论的雷达成像技术与应用研究进展[J]. 电子与信息学报, 2016, 38(2):495-508.

[9]SUN Chao, WANG Baoping, FANG Yang, et al. High-Resolution ISAR Imaging of Maneuvering Targets Based on Sparse Reconstruction[J]. Signal Processing, 2015, 108(1):535-548.

[10]叶淋美. 基于压缩感知的雷达信号处理应用研究[D]. 厦门：厦门大学, 2014.

[11]LIU Hongchao, JIU Bo, LIU Hongwei, et al. A Novel ISAR Imaging Algorithm for Micromotion Targets Based on Multiple Sparse Bayesian Learning[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10):1772-1776.

[12]洪灵,戴奉周,刘宏伟. 基于三维重构的空间目标进动参数估计方法[J]. 电波科学学报, 2015, 30(2):237-243.

[13]王保平,方阳,孙超,等. 压缩感知窄带自旋目标雷达成像[J]. 遥感学报, 2015, 19(2):254-262. WANG Baoping, FANG Yang, SUN Chao, et al. Narrowband Radar Imaging for Spinning Targets Based on Compressed Sensing[J]. Journal of Remote Sensing, 2015, 19(2):254-262.(in Chinese)

[14]MOHIMANI H, BABAIE-ZADEH M, JUTTEN C. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed0Norm[J]. IEEE Trans on Signal Processing, 2009, 57(1):289-301.