黄土高原盆地土壤有机质与影响因子的空间多尺度关系

朱洪芬,南 锋,徐占军,荆耀栋,段永红,毕如田

山西农业大学资源环境学院,太谷 030801

土壤有机质含量不仅是肥力的重要指标[1],也是全球碳循环中重要的源和汇[2- 3]。前人已对不同尺度下土壤有机质的空间变异性进行了大量研究,证明了在特定尺度下,土壤的异质性与外部环境因素共同影响有机质的空间分布[3- 5]。因此,建立土壤有机质与影响因子的准确关系成为间接理解有机质空间变异性的方法之一。然而,由于不同尺度下的土壤有机质含量与影响因子的空间关系具有较大差异性[5- 6],当某一因子在不同尺度同时影响土壤有机质空间分布时,可能造成该因子与土壤有机质的非线性关系。因此,应用传统统计方法建立土壤有机质预测模型时,模型的精确度与可靠性可能会受到较大影响。

当前,在环境因子与土壤属性的空间多尺度关系的研究中,多采用Pearson相关分析[7]、小波分析[8- 9]和多维分析[10]等方法。应用该类方法的前提是假设相关环境因子对土壤属性空间分布的影响为线性且平稳,但此类假设可能与土壤属性的实际空间分布不相符。多元经验模态分解(multivariate empirical mode decomposition, MEMD)由Huang等首次提出,是与小波分析相对应的另一种多尺度分析方法,可根据数据本身的尺度特征经验性的将空间数据分解在多个表征尺度上[11],避免了线性和平稳性的假设。尽管MEMD法具有明显优势,但尚未广泛应用于土壤属性尺度问题的相关研究中。

黄土高原由第四纪冰期厚层黄土堆积而成,是全球水土流失最严重的地区之一[12]。黄土高原盆地内多平原与丘陵,海拔高度相对较低,温湿环境适宜,有利于农业生产[13]。由于土地利用形式存在多样性及植被覆盖的斑块化与破碎化,造成了本区域内土壤有机质分布的无序性及影响因子对有机质作用的非线性[14]。因此,研究该区域土壤有机质与相关因子间的空间多尺度关系可为有机质管理提供理论依据。鉴于MEMD法可用于空间数据的非线性和非平稳的空间多尺度分析,因此本研究假设该方法也可用于土壤有机质与相关因子间的空间多尺度研究中。本文以山西省太原盆地为研究区域,分析盆地内不同部位土壤有机质的表征尺度,以及土壤有机质与影响因子的空间多尺度关系,并实现有机质含量在采样尺度上的预测。

1 研究材料与方法

1.1 研究区概况

太原盆地地处黄土高原中东部、山西省中部(36°55′—38°12′N,111°42′—113°02′E),属典型的黄土集中分布地带。盆地南北长约150 km,东西宽为12—60 km,区域包括汾河流域中游,总面积达6159 km2,人口数量占全省近1/3。该区气候属暖温带大陆性季风气候类型,年日照总时数为2360—2796 h,年平均降水量为420—457 mm,总降水量由南到北逐渐减少。境内平均海拔800—900 m,东、西、北三面环山,中部为冲积平原,年平均气温7.8—10.3℃。中部平原以冲洪积亚砂粘土质黄土为主,边山丘陵以风积厚层亚砂黄土为主。境内土壤类型主要有潮土、盐化潮土、石灰性褐土和褐土性土等四类,主要农作物为冬小麦和玉米,是山西省主要农业生产区。

1.2 样品的采集与处理

根据海拔与汾河流向,沿北东-南西方向将盆地划分为上、中、下三部位。结合野外调查和相关图件分析,避开大型建设用地后,在盆地不同位置设置3条采样带(带1海拔：742—894 m；带2海拔：723—807 m；带3海拔：707—1002 m),每条样带长约42 km,以330 m间隔设置采样点。若某一样点落于建设用地或道路等非耕地上,则在离该点最近的耕地上取样,并尽量使所有样点在一条直线上。采样带1、2和3分别包含121、128和134个样点,共计383个(图1)。

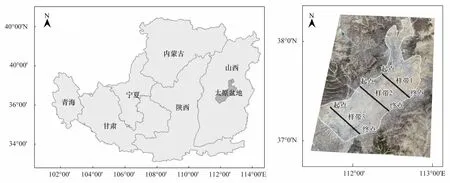
图1 研究区地理位置及采样点分布Fig.1 Geographical location of study area and sample points distribution

土样采于2016年3月22—31日。采样时,首先利用GPS查找样点位置,并采用“S”形布点法进行样品采集。使用螺旋取土钻钻取0—20 cm耕层土壤样品5个,混合后作为本采样点样品。样品混合均匀后经风干、磨碎、过2 mm孔筛后分为两份,分别用于土壤光谱和土壤有机质、质地测试。使用环刀(高5 cm,体积100 cm3)在“S”形样点中心处采集表层原状土样,烘干后(105℃,10 h)测定土壤容重。采用重铬酸钾-外加热法测定土壤有机质含量[15],采用沉降法测定土壤质地[16],采用地物光谱仪(美国ASD FieldSpec3)测定土壤光谱。其中,光谱范围为350—2500 nm,数据重采样间隔为1 nm[17]。

1.3 MEMD原理

MEMD是经验模态分解(empirical mode decomposition, EMD)的扩展,可直接将获取的数据应用于空间域,并根据空间数据特征,将其分解为多个空间序列。MEMD对数据的分解基于如下假设,即在给定的空间内,空间数据存在简单的不同频率相互叠加的震荡模式[11]。自然界中,事物整体变异性受多种过程影响,并在不同尺度以不同强度发生[18]。其中,同一尺度发生的过程可以分解为相同的本征模函数(Intrinsic Mode Function, IMF)。定义IMF需满足以下条件：1)可以是线性或非线性,该IMF在整个数据范围内,局部极值点和过零点的个数必须相等或最多相差一个。其中,局部极值点表示一个函数可以提取的最小值或最大值,过零点表示函数改变其符号的点。2)该数据的震荡对局部平均值对称,即在任一数据点处由局部极大值和极小值定义的平均包络值为0。上包络线和下包络线由通过分别样条插值全部局部最大值或最小值产生。根据该定义,IMF可通过“筛选(sifting)”过程分解任意函数后获取,IMF的方差贡献百分比(%)可通过下列公式计算：

(1)

单个IMF对整体方差的贡献率决定了每个IMF的相对重要性,因此,也可决定在不同尺度上发生过程的相对重要性[19],即方差分解法。通过计算每个IMF震荡的平均次数,可确定对应IMF的平均尺度。然而,由于土壤属性与环境因子之间存在非线性关系,使得局部范围内无法预测其周期或尺度。瞬时尺度可提供每个IMF所代表的尺度范围,并通过Hilbert变换得到的瞬时频率来获取。EMD可将空间数据分解为不同的表征尺度,而Hilbert谱分析可计算它们在每个尺度和位置的能量与频率,便于从不同尺度的数据中提取不同位置的频率。

应用MEMD时要求计算空间数据序列的局部平均值,而对于多个空间数据序列可能无法直接定义最大值和最小值。为解决该问题,Rehman和Mandic[20]建议,在N维空间内通过不同方向的投影创建多个N维包络,取其均值可作为局部平均值。

(1)产生一个合适的方向矢量X数据集；

(2)计算空间序列V(s)沿给定方向Xθk的投影pθk(s)；

(5)通过下式计算包络曲线的均值M(s)；

(2)

(6)利用D(s)=V(s)-M(s)提取D(s)。若D(s)满足终止迭代准则,则从步骤(1)开始重复以上步骤,并计算残差V(s)-D(s)。否则,从步骤(2)开始重复计算D(s)。残差变为单调函数且再无法提取IMF时,分解过程终止。该残差可表明原始数据的变化趋势。

1.4 数据预处理

去除土壤光谱数据中噪声影响较大的350—399和2451—2500 nm边缘波段,利用MATLAB将可见光-近红外波段(401—2450 nm)2050个土壤光谱数据进行主成分压缩,并将压缩后前两个主份(占整体方差的95%以上)选作综合影响因子。

将土壤有机质与地形因子(高程、坡度和地形湿度指数)、物理性状(容重、砂粒、壤粒和黏粒含量)、光谱主份数据等组成多元数据序列,利用MEMD法将各样带数据序列分解为不同IMF。根据MEMD算法,通过多元序列数据中的N个IMF共同震荡模式来识别每个“共同尺度”[20]。在不同的数据源中,MEMD将相似的尺度归为一组,代表相关发生过程的实际尺度。

计算各样带在采样尺度与单个IMF(表征尺度)和残差下的土壤有机质与地形因子、土壤物理性状、土壤光谱主份等因子的Pearson相关系数。采用逐步多元回归模型,利用地形、土壤物理性状和光谱主份等被分解的各IMF和残差,预测土壤有机质在对应尺度和残差处的含量值。最后,通过单个IMF和残差预测出的对应土壤有机质值,利用如下公式估测采样尺度上有机质含量：

(3)

采用由实测值和预测值计算出的决定系数(coefficient of determination,R2)、均方根误差(root mean squared error, RMSE)、标准化均方根误差(normalized root mean square error, NRMSE)和相对预测偏差(residual prediction deviation,RPD)评价土壤有机质预测精度,各参数计算公式如下：

(4)

(5)

(6)

(7)

2 结果与分析

2.1 采样尺度上土壤有机质与影响因子的关系

表1为利用Pearson′s相关分析法对土壤有机质与地形因子、土壤物理性状、光谱主份等影响因子的线性相关度进行分析的结果。在样带1上,有机质含量与高程、容重和光谱主份1显著相关；在样带2上,与高程、坡度、容重、砂粒、壤粒、黏粒和光谱主份1显著相关；在样带3上,与高程、容重、砂粒、壤粒和光谱主份1显著相关。在全部样带上,有机质与高程、容重、砂粒、壤粒和光谱主份1显著相关,表明在采样尺度上研究区内土壤有机质主要受这五个影响因子的作用,相关局部尺度的发生过程(如生物活动、耕作措施等)扰乱了其他影响因子对土壤有机质的作用,因此表现为无显著相关性。土壤有机质与物理性状的相关性顺序为样带2>样带3>样带1。样带2中,地形因子、容重、质地对土壤有机质含量的影响最强。这些结果表明,在采样尺度上,地形因子与土壤物理性状对盆地中部土壤有机质含量的影响最强。

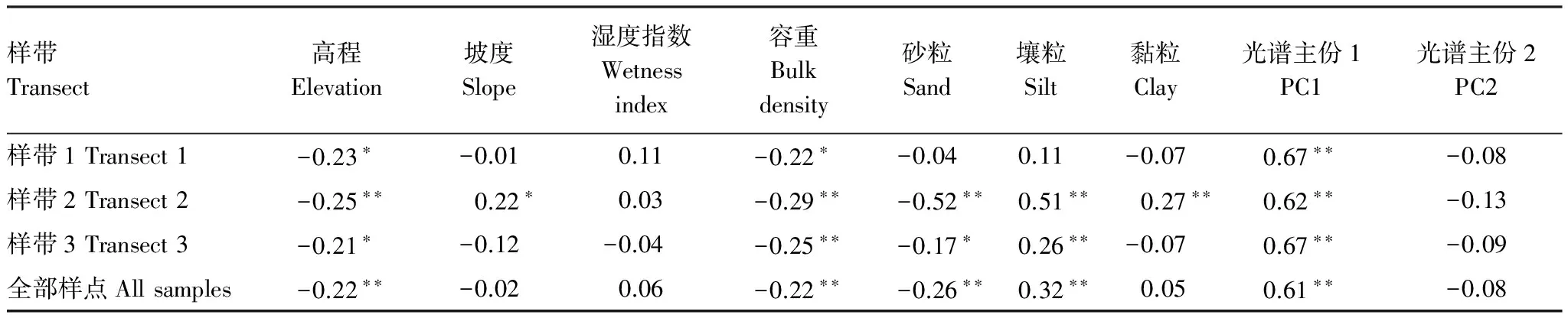
表1 采样尺度上土壤有机质与影响因子的相关系数

*显著性水平为P<0.05；**显著性水平为P<0.01

如表2所示,本研究采用逐步多元回归法构建了土壤有机质预测模型。各相关因子(样带1中为壤粒、光谱主份1和2,样带2中为坡度、容重、壤粒和光谱主份1,样带3中为高程、容重、砂粒、黏粒、光谱主份1和2)对样带1、2和3中土壤有机质含量的预测能力分别达到了52%、56%和54%。

2.2 土壤有机质与影响因子的空间多尺度关系

利用MEMD法将土壤有机质与影响因子的多元数据序列分解为不同的IMF。土壤有机质的IMF如图2所示。随着IMF增大,土壤有机质空间序列的震荡周期变长,表明土壤有机质的表征尺度随IMF变大而增加。同时,各样带在IMF1处的震荡幅度均较大,表明在该尺度处的空间变异性较大。土壤有机质的残差序列表明了原始数据的变换趋势,即样带1中土壤有机质的变化趋势比较明显,且与样带2一起呈逐渐减小的趋势,而样带3呈先稳定后增大的趋势。各样带上,土壤有机质与影响因子均具有相同的IMF个数与类似的震荡幅度。因此,本研究利用Hilbert变换识别各样带不同因子的IMF对应的空间尺度,并将所有因子的尺度取其均值,获取该样带上每个IMF的对应尺度(表3)。样带中各因子的IMF对应尺度的变异系数随IMF变大而增大,表明在小尺度处土壤有机质和影响因子具有相近的表征尺度。样带2和3中,1—4 IMF尺度较接近,即在< 5000 m尺度的发生过程约在表征尺度960、1500、2600和4400 m处；5—8 IMF尺度差异较大,即样带2发生过程的表征尺度约为8573、10901、11591和23659 m,而样带3约为6753、11806和12292 m。该结果表明,盆地中、下部在小尺度处的表征尺度较接近；随着尺度的变大,表征尺度的差异性增大。另外,盆地上部的表征尺度与盆地中部、下部的差异较大。

表2 基于影响因子的土壤有机质的逐步多元回归预测模型

Elevation：高程；Slope：坡度；TWI：地形湿度指数,topographic wetness index；BD：容重,bulk density；Sand：砂粒；Silt：壤粒；Clay：黏粒；PC1：光谱主份1；PC2：光谱主份2；括号中的数据表示标准偏回归系数

图2 三条样带中土壤有机质被分解的IMF和残差Fig.2 Separated IMFs and residues for SOM at the three transects

样带中有机质与影响因子的IMF方差百分比如表4所示。样带1中,土壤有机质方差百分比主要分布在IMF1和2处(18.62%和19.41%),表明盆地上部的土壤有机质变异性主要在1011和1725 m尺度处。样带2中,其方差百分比主要分布在IMF1和5处(30.61%和16.91%),表明盆地中部的土壤有机质变异性主要在982和8573 m尺度处。样带3中,其方差百分比主要分布在IMF1、5和6处(17.62%、12.53%和20.46%),表明该处土壤有机质变异性主要表现在960、6753和11806 m尺度处。总之,整个区域内尺度约1000 m均表现为土壤有机质的主要表征尺度。同时,盆地上部土壤有机质的主要表征尺度是小尺度,即< 2000 m；盆地中部的是小尺度和中尺度,即1000、8000 m；盆地下部的是小尺度、中尺度和大尺度,即1000、7000、12000 m。这些结果表明,该区域内垂直于汾河流向的土壤有机质主要表征尺度沿河流方向表现分散。

表3 三个样带中土壤有机质IMF的对应尺度/m

括号中的数据表示土壤有机质和影响因子IMF对应尺度的变异系数值(%)

表4 三条样带中土壤有机质的每个IMF和残差占原始数据方差的百分比

通过观察各影响因子的IMF方差百分比发现,高程除在第三条样带IMF6处值(21.07%)较大外,其余主要分布在残差部分(3条样带分别为75.93%、72.83%和70.04%),表明高程的主要表征尺度比该实验提取的尺度大。在样带1中,除高程外的其他影响因子的表征尺度主要在IMF1和2处,即小尺度1011和1725 m处。样带2中,坡度、砂粒和壤粒含量的表征尺度主要在IMF1和5处(尺度982 和8573 m),其余影响因子主要在IMF1和2处(尺度982 和1530 m)。样带3中,除坡度(IMF1、3和6处)、黏粒(IMF1和3处)、光谱主份1和2(IMF1、5和6处)外,其余影响因子主要在IMF1和2处(960和1504 m)。上述结果表明,除高程外相关因子的变异性主要发生在小尺度处。

与采样尺度上的相关性不同,土壤有机质与影响因子多尺度相关性见表5。除样带3中IMF2外,高程与土壤有机质的相关性主要表现在大尺度,即样带1为IMF5、6和残差；样带2为IMF6、7、8和残差；样带3为IMF6、7和残差。这些结果表明,盆地内高程对土壤有机质的影响主要表现在大尺度约10000、12000、23000 m处。坡度与有机质关系在样带1中较弱,主要表现在大尺度IMF6和残差处,在样带3中主要表现在IMF2、5、6、7和残差处；而与样带2中有机质关系最为显著,即除IMF1和3外,其余均显著相关。地形湿度指数与土壤有机质的空间多尺度关系表明,在盆地中部两者的关系最明显,主要表现在尺度982、2588、4487、8573、10901、11591 m处。盆地下部两者的关系较明显,这与采样尺度上两者的关系不一致。土壤容重与有机质的多尺度关系表明,在盆地上、中部小尺度约1000 和1500 m处,中、下部尺度约3000 m处,下部尺度约4500 和6700 m处,上部尺度约5400和9500 m处及在整个盆地内大尺度> 10000 m处,两者显著相关。土壤质地(包括砂粒、壤粒和黏粒)与有机质的多尺度关系表明,壤粒含量对土壤有机质的多尺度关系最显著,即除样带1中IMF4外,二者在所有表征尺度均显著相关。光谱主份与有机质的多尺度关系表明,在研究样带中的所有表征尺度上,光谱主份1均与有机质含量显著相关,而光谱主份2的相关性明显弱于光谱主份1。总之,相关因子对土壤有机质的影响随尺度增大而呈增大趋势。另外,对于残差部分,土壤有机质与影响因子的相关性均达到0.05的显著性水平,表明被选定的影响因子与土壤有机质存在一定关系。

表5 基于MEMD的不同IMF和残差的土壤有机质与影响因子的相关系数

*显著性水平为P<0.05；**显著性水平为P<0.01

2.3 基于与影响因子多尺度关系的土壤有机质预测

如表6所示,本研究采用逐步多元回归获取了每个IMF土壤有机质的预测模型。从中可以看出,除样带3中IMF2外,所有预测模型的可调整R2均在0.44—1.00之间变化,且随IMF增大而增大。可调整R2的变化趋势表明,尺度越大,对土壤有机质的预测精度越高,且模型中所选因子对有机质的影响更强烈。基于所有IMF和残差的有机质预测结果,本研究采用逐步多元回归法进行采样尺度上土壤有机质的预测,结果列于表7。结果表明：采样尺度上各样带中土壤有机质预测值和实测值的R2分别为0.90、0.86和0.91,显著高于采样尺度上直接利用逐步多元回归拟合的结果(0.52、0.56和0.54)。通过MEMD方法获取的RMSE和NRMSE显著低于直接逐步多元回归的预测结果,而RPD显著高于直接逐步多元回归的预测结果。基于上述评价参数的比较,可以得出采用MEMD对土壤有机质的预测精度高于基于原始数据的简单逐步多元回归预测的结论。

表6基于经验模态分解的每个IMF和残差的土壤有机质逐步多元回归预测模型和回归统计特征(F值和可调整R2)

Table6Predictiveequationsandregressionstatistics(F-value and adjustedR2)forSOMforeachIMFandresidueusingstepwisemultiplelinearregressionbasedonmultivariateempiricalmodedecomposition

样带TransectsIMF公式FunctionFR2样带1IMF10．03+21．31(0．43)Silt+3．77(0．68)PC1-4．94(0．12)PC242．00．52Transect1IMF20．01+1．06(0．17)TWI-12．01(0．19)BD-27．28(0．46)Sand-9．66(0．26)Clay+3．63(0．53)PC1-21．01(0．42)PC230．00．61IMF30．05+0．07(0．16)Elevation+0．26(0．13)Slope+1．15(0．24)TWI+9．74(0．44)BD+22．34(0．37)Silt-18．42(0．31)Clay+3．63(0．81)PC153．20．77IMF4-0．06+0．03(0．09)Elevation-0．34(0．17)Slope+4．96(0．07)Silt+0．69(0．90)PC1142．60．83IMF5-0．03+0．23(0．48)Elevation+1．46(0．70)Slope+1．55(0．27)TWI-7．08(0．48)BD+58．61(0．59)Silt+6．17(0．10)Clay+4．54(0．72)PC1-0．21(0．24)PC21808．60．99IMF60．01+0．46(0．98)Elevation+3．62(0．75)Slope+6．44(0．18)TWI-3．75(0．25)BD-157．71(2．27)Sand-204．82(1．49)Clay+7．41(1．38)PC1+7．49(0．07)PC261428．31．00残差-1007．72+11．61(2．02)Slope+138．15(1．38)BD+19．51(2．44)PC1+251．95(4．02)PC2394573．81．00样带2Transect2IMF10．07+0．49(0．14)Slope-1．41(0．27)TWI-10．56(0．26)BD+6．77(0．12)Silt+3．32(0．51)PC121．40．47IMF20．03-0．16(0．11)Elevation-1．03(0．41)Slope-7．91(0．20)BD-3．33(0．37)Sand-29．89(0．59)Clay+1．95(0．4)PC1+4．66(0．15)PC224．80．59IMF30．08-0．58(0．30)Elevation-1．12(0．29)TWI-5．67(0．13)BD-15．07(0．26)Clay+4．62(0．92)PC1-17．81(0．44)PC248．80．71IMF4-0．07+0．71(0．28)Slope+1．71(0．36)TWI-2．56(0．06)BD+1．42(0．16)Silt+4．30(0．79)PC1-13．93(0．34)PC2165．50．89IMF5-0．01-0．55(0．51)Elevation-0．52(0．18)Slope+2．67(0．33)TWI+30．02(0．72)Silt-28．44(0．51)PC2418．70．95IMF60．33(0．85)Elevation+0．57(0．52)Slope-2．42(1．22)TWI-37．26(0．68)BD+18．02(0．71)Clay+9．25(2．32)PC1-16．24(0．41)PC210392．01．00IMF70．16(0．30)Elevation-2．73(0．72)TWI-11．86(0．34)Sand-16．14(0．17)Silt+11．10(1．39)PC1-33．83(0．25)PC212571476．71．00IMF8-0．03(0．18)Elevation+1．50(0．10)TWI-46．05(1．10)BD+11．81(0．36)PC21525552．41．00残差-32．33+1．41(0．42)Slope+32．04(0．69)Clay+17．29(0．17)PC2816066．51．00样带3IMF1-0．06-23．23(0．43)Sand-19．10(0．27)Clay+3．81(0．61)PC1-11．97(0．27)PC225．40．44Transect3IMF2-0．52(0．16)TWI+13．43(0．27)Silt+3．26(0．50)PC1-14．41(0．31)PC219．50．38IMF30．01-0．11(0．27)Elevation+0．44(0．18)Slope+1．03(0．33)TWI-9．36(0．21)BD+11．81(0．28)Silt+2．54(0．50)PC1-6．04(0．18)PC217．20．49IMF40．20+2．98(0．66)TWI+12．61(0．26)BD+4．53(0．31)Silt-17．50(0．19)Clay+5．77(1．01)PC1216．30．89IMF50．05-0．16(0．45)Elevation+2．91(0．44)Slope+1．01(0．12)TWI-15．34(0．19)BD-8．10(0．07)Silt-47．86(0．35)Clay+2．52(0．53)PC1-32．90(0．64)PC2323．90．95IMF6-0．4-0．24(2．08)Elevation+6．90(1．14)Slope-13．72(1．36)TWI-18．46(0．08)BD-48．27(0．22)Silt+243．41(0．72)Clay2766．60．99IMF77．91E-5-0．03(0．15)Elevation-2．31(0．21)Slope-1．16(0．03)TWI-78．23(0．46)BD+3．64(0．49)PC1-16．36(0．23)PC21487634911．00残差117．97-0．73(0．26)Slope+46．93(0．84)Silt-43．50(1．72)PC214528671．00

Elevation：高程；Slope：坡度；TWI：地形湿度指数,topographic wetness index；BD：容重,bulk density；Sand：砂粒；Silt：壤粒；Clay：黏粒；PC1：光谱主份1；PC2：光谱主份2；括号中的数据表示标准偏回归系数

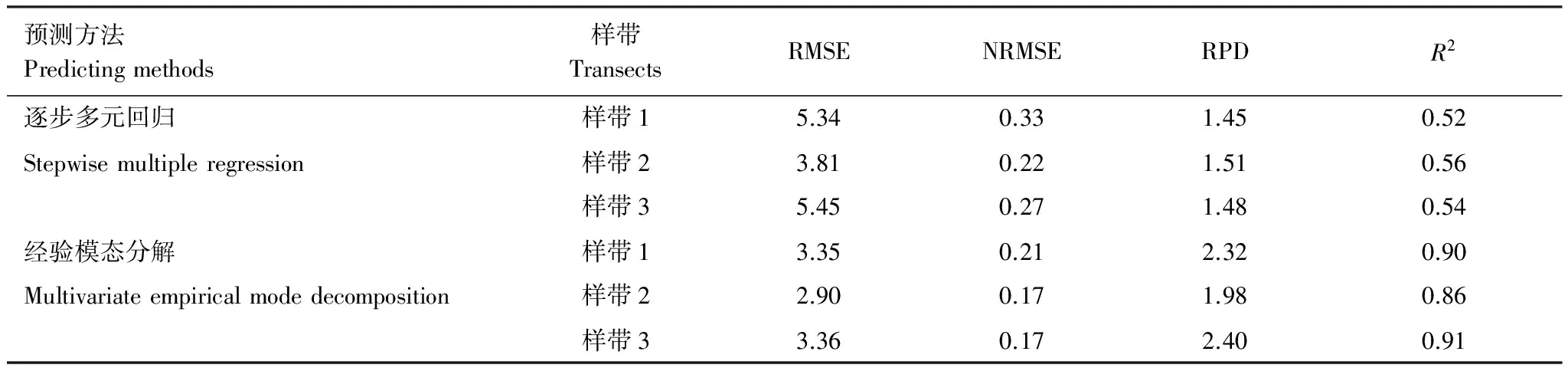
表7 评价土壤有机质预测精度的相关参数

RMSE：均方根误差,root mean squared error；NRMSE：标准化均方根误差,normalized root mean square error；RPD：相对预测偏差,residual prediction deviation

采样尺度上土壤有机质实际值与单个IMF或残差处预测值及变量预测有机质值的相关系数如图3所示。该相关系数的比较可反映每一IMF相对于采样尺度上有机质预测结果的重要性程度。结果表明,样带1中有机质预测的主要贡献者是IMF6；样带2中主要贡献者是IMF5；样带3中主要贡献者是IMF6。即盆地上部尺度12375 m处、中部尺度8573 m处和下部尺度11806 m处对采样尺度上有机质的预测起主要作用。另外,可能代表更大尺度的残差在样带1中的比重较大,其次是样带2,最后是样带3,表明被分解的IMF能够很好解释土壤有机质变异性的顺序为盆地的下部>中部>上部。

图3 采样尺度上土壤有机质实际值与单个IMF或残差处预测值及变量预测有机质值的相关系数Fig.3 Coefficient of determination between SOM at the measurement scale and predicted IMFs (residue) or total SOM predicted by each variable

土壤有机质的变异性主要是土壤本身异质性、地形、植被、人类活动等综合因素影响的结果。不同尺度的某一因子对有机质预测值与采样尺度上实测值的相关系数如图3所示。该结果可表示每一因子对采样尺度上土壤有机质预测的相对重要性。3条样带中光谱主份1(综合因子)是有机质预测中最重要的影响因子。此外,样带1中容重、样带2中砂粒和壤粒含量、样带3中地形湿度指数、坡度和容重对其有机质预测也起了重要作用。总之,地形因子、土壤容重和光谱主份对样带3中有机质的影响最为明显,土壤质地对样带2中有机质的影响最为明显,且影响顺序为中部>下部>上部,而样带1中土壤有机质受地形因子、土壤容重和质地的影响程度最弱。

与传统回归分析相比(表2),MEMD可捕捉到样带1中容重、样带2中砂粒及样带3中地形湿度指数和坡度对有机质的影响。同时,回归方程中标准回归系数也可表示这些影响因子在每一尺度上对有机质预测的相对重要性(表6)。在样带1中,光谱主份1对所有表征尺度上土壤有机质预测起显著影响。土壤质地在小尺度(≤3078 m)和大尺度(≥9535 m)处对有机质预测起显著影响。同时,地形因子对有机质预测的影响随尺度增大而增强,如坡度因子在IMF3、4、5和6处系数分为0.13、0.17、0.70和0.75。土壤容重对IMF2、3、5、6和残差处有机质预测都有显著影响。因此,容重对样带1采样尺度上有机质预测的贡献主要体现在这几个尺度上的综合作用。

在样带2中,由于IMF7和8中有机质预测值与采样尺度上实测值的相关系数不显著,故可忽略(图3)。从IMF1到6处,地形因子对有机质预测的影响逐渐增强。土壤容重和质地对不同尺度有机质预测的影响无明显规律。砂粒含量对采样尺度上有机质预测的影响主要体现在IMF2处。在样带3中,地形因子对有机质预测的影响随尺度的增大而增强,且在IMF6处达到最大值,然后随尺度增大而减小,且湿度指数对样带3中有机质预测的影响最为明显。土壤质地在其小尺度IMF1和大尺度IMF6处影响最强。容重在IMF3、4和7处对有机质预测有稳定影响,其余尺度不明显。综上,与传统回归分析相比,MEMD方法在某些表征尺度可捕捉到相关因子对有机质分布的影响,故其预测精度高于采用传统回归分析方法。

土壤有机质实测值和预测值的局部小波如图4所示。与MEMD相比,逐步多元回归预测误差在样带1中主要是在位置19.8—33.0 km处局部高估,造成尺度1—2和4 km处局部方差的增大；样带2中,主要是在位置19.8—33.0 km处局部低估,造成尺度4—8 km处局部方差的减小；样带3中,主要是在位置19.8—36.3 km处局部高估,造成8 km处局部方差的增大。

图4 土壤有机质实测值和逐步多元回归、MEMD法预测值的局部小波图Fig.4 Local wavelet spectrum of measured and predicted SOM by SMLR or MEMD

3 讨论

本研究采用MEMD法将太原盆地不同位置的土壤有机质空间序列分解为不同的表征尺度,发现主要表征尺度在1000 m处。因此,在利用栅格数据存储该盆地内土壤属性时,建议将表层土壤有机质最佳格网宽度设置为1000 m,以便捕捉到有机质较大的空间变异性。盆地上部残差的方差百分比较大(24.19%),可能是需设计更长的采样带才可利用MEMD识别的更大尺度。同时,盆地上部的表征尺度与中、下部差异较大,可能是由于盆地上部距太原和晋中市等大、中型城市较近,人为活动造成土地利用破碎。此外,有机质空间序列在垂直河流方向上的主要表征尺度沿汾河流域方向表现呈分散状态,表明沿河流方向的相关因子对有机质空间分布影响的主导性增强。

在采样尺度和空间多尺度关系上,盆地中部土壤有机质分布与地形因子、容重和土壤质地的相关性最强,这可能是由该区处于侵蚀平原(上部)与陷落盆地(下部)的交界处的特殊地质条件造成[23]。在采样尺度上,盆地中部有机质与光谱主份1的相关性最弱,可能是由于中部区域土壤有机质的变异性较小,导致有机质与土壤光谱之间的相关性减弱[17]。另外,有机质与某些因子在采样尺度不存在显著相关,但是二者的空间多尺度关系在某些表征尺度呈显著相关,表明土壤有机质与影响因子的空间多尺度关系能获取更多信息。同时,基于有机质与相关因子空间多尺度关系的有机质预测精度显著高于采样尺度上直接利用逐步多元回归分析的结果,进一步表明单一尺度(采样尺度)的简单分析难以揭示两者的复杂关系。

MEMD法适用于分析非线性、非平稳数据序列的空间多尺度关系[24]。由于该理论建立时间尚短,在土壤属性的空间多尺度研究中还未广泛应用。同时,MEMD法也存在一定缺陷。Hu和Si研究结果表明,每条样带的所有IMF和残差的方差百分比之和并不等于100%[25]。此外,与小波分析不同,MEMD法会针对不同采样带分解出不同的表征尺度,特定样带的研究结果不能推广。因此,MEMD法重在分析其发生过程,在结果验证方面存在缺陷。

4 结论

本文采用MEMD法分析了太原盆地土壤有机质与影响因子的空间多尺度关系,主要结论如下：

(1)盆地上部主要表征尺度为1011 和1725 m,中部为982 和8573 m,下部为960 、6753 和11806 m。整个盆地内,尺度约1000 m处是土壤有机质的主要表征尺度,且盆地内垂直河流方向的有机质序列主要表征尺度沿河流方向表现分散。

(2)土壤有机质与影响因子在采样尺度和MEMD空间多尺度的相关性顺序为：盆地中部>下部>上部。

(3)在3种景观样带上,光谱主份1与有机质的相关性均显著。其次,盆地上部的容重、中部的砂粒和下部的地形湿度指数对其影响较明显,而在采样尺度上盆地下部二者的关系并不显著。因此,单一尺度分析不能够全面揭示土壤有机质与相关因子在所有空间尺度上的复杂关系,而MEMD法对有机质的预测精度要显著高于直接利用逐步多元回归分析。

致谢：感谢郭颖、王鹏和徐振对样品采集和测试提供的帮助。

[1] Bauer A, Black A L. Quantification of the effect of soil organic matter content on soil productivity. Soil Science Society of America Journal, 1994, 58(1): 185- 193.

[2] Lal R. Soil carbon sequestration impacts on global climate change and food security. Science, 2004, 304(5677): 1623- 1627.

[3] Hu K L, Wang S Y, Li H, Huang F, Li B G. Spatial scaling effects on variability of soil organic matter and total nitrogen in suburban Beijing. Geoderma, 2014, 226- 227: 54- 63.

[4] Li D F, Gao G Y, Lü Y H, Fu B J. Multi-scale variability of soil carbon and nitrogen in the middle reaches of the Heihe River basin, northwestern China. Catena, 2016, 137: 328- 339.

[5] Zhou Y, Biswas A, Ma Z Q, Lu Y L, Chen Q X, Shi Z. Revealing the scale-specific controls of soil organic matter at large scale in Northeast and North China Plain. Geoderma, 2016, 271: 71- 79.

[6] Zhu H F, Bi R T, Duan Y H, Xu Z J. Scale-location specific relations between soil nutrients and topographic factors in the Fen River Basin, Chinese Loess Plateau. Frontiers of Earth Science, 2016: 1- 10, doi: 10.1007/s11707-016-0587-y.

[7] She D L, Shao M A, Hu W, Yu S E. Variability of soil water-physical properties in a small catchment of the Loess Plateau, China. African Journal of Agricultural Research, 2010, 5(22): 3041- 3049.

[8] Zhu H F, Hu W, Bi R T, Peak D, Si B C. Scale-and location-specific relationships between soil available micronutrients and environmental factors in the Fen River basin on the Chinese Loess Plateau. Catena, 2016, 147: 764- 772.

[9] Liu Q J, Shi Z H, Fang N F, Zhu H D, Ai L. Modeling the daily suspended sediment concentration in a hyperconcentrated river on the Loess Plateau, China, using the Wavelet-ANN approach. Geomorphology, 2013, 186: 181- 190.

[10] Wang D, Fu B J, Zhao W W, Hu H F, Wang Y F. Multifractal characteristics of soil particle size distribution under different land-use types on the Loess Plateau, China. Catena, 2008, 72(1): 29- 36.

[11] Huang N E, Shen Z, Long S R, Wu M C, Shih H H, Zheng Q A, Yen N C, Tung C C, Liu H H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903- 995.

[12] She D L, Shao M A, Timm L C, Reichardt K. Temporal changes of an alfalfa succession and related soil physical properties on the Loess Plateau, China. Pesquisa Agropecuária Brasileira, 2009, 44(2): 189- 196.

[13] 刘志鹏. 黄土高原地区土壤养分的空间分布及其影响因素[D]. 北京: 中国科学院研究生院, 2013.

[14] Hu W, Shao M A, Si B C. Seasonal changes in surface bulk density and saturated hydraulic conductivity of natural landscapes. European Journal of Soil Science, 2012, 63(6): 820- 830.

[15] 鲍士旦. 土壤农化分析(第三版). 北京: 中国农业出版社, 2013.

[16] 庞奖励, 黄春长, 贾耀峰. 不同方法测定黄土和古土壤样品粒度的比较. 陕西师范大学学报: 自然科学版, 2003, 31(4): 87- 92.

[17] 南锋, 朱洪芬, 毕如田. 黄土高原煤矿区复垦农田土壤有机质含量的高光谱预测. 中国农业科学, 2016, 49(11): 2126- 2135.

[18] Goovaerts P. Geostatistical tools for characterizing the spatial variability of microbiological and physico-chemical soil properties. Biology and Fertility of Soils, 1998, 27(4): 315- 334.

[19] Oladosu G. Identifying the oil price-macroeconomy relationship: An empirical mode decomposition analysis of US data. Energy Policy, 2009, 37(12): 5417- 5426.

[20] Rehman N, Mandic D P. Multivariate empirical mode decomposition. Proceedings of the Royal Society A, 2010, 466(2117): 1291- 1302.

[21] Ur Rehman N, Mandic D P. Filter bank property of multivariate empirical mode decomposition. IEEE Transactions on Signal Processing, 2011, 59(5): 2421- 2426.

[22] Zhao X M, Patel T H, Zuo M J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery. Mechanical Systems and Signal Processing, 2012, 27: 712- 728.

[23] 姜佳奇, 莫多闻, 吕建晴, 廖奕楠, 鲁鹏, 任小林. 山西太原盆地全新世地貌演化及其对古人类聚落分布的影响. 古地理学报, 2016, 18(5): 895- 904.

[24] She D L, Zheng J X, Shao M A, Timm L C, Xia Y Q. Multivariate empirical mode decomposition derived multi-scale spatial relationships between saturated hydraulic conductivity and basic soil properties. Clean-Soil, Air, Water, 2015, 43(6): 910- 918.

[25] Hu W, Si B C. Soil water prediction based on its scale-specific control using multivariate empirical mode decomposition. Geoderma, 2013, 193- 194: 180- 188.