单磨头打磨钢轨廓形的仿真分析

邱俊兴，许玉德，卢 野，沈坚锋，李凤煜

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.中铁二院工程集团有限责任公司，四川 成都 610031）

单磨头打磨钢轨廓形的仿真分析

邱俊兴1，许玉德1，卢 野2，沈坚锋1，李凤煜1

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.中铁二院工程集团有限责任公司，四川 成都 610031）

钢轨打磨是铁路线路重要的养护维修技术，唯有高精度的打磨才能最大限度的延长钢轨寿命，深入了解钢轨廓形打磨的规律对提高打磨精度有重要意义。以PGM-96C型打磨车为例，基于迹线法求解砂轮与钢轨接触位置，提出单磨头打磨量的计算方法，并通过现场试验进行验证，最后基于该计算方法对不同打磨角度下的单磨头打磨钢轨廓形进行仿真分析，结果表明，在17.6 kW的打磨功率下，砂轮摆角为0°时，钢轨打磨深度为0.08 mm，打磨宽度为12.17 mm，随着砂轮摆角增大，钢轨打磨深度增大，而打磨宽度减小，砂轮摆角增大到20°以上时，打磨深度维持在0.22 mm左右，打磨宽度维持在4.70 mm左右。

钢轨打磨；单磨头；仿真分析；打磨角度

钢轨打磨能够消除轨头的伤损和疲劳，延长钢轨使用寿命，已成为线路养护维修的一种重要手段[1－2]。随着打磨技术不断发展，打磨精度越来越受到关注，研究发现，钢轨打磨廓形的精细化控制对轮轨接触关系和钢轨寿命有着重要的影响，唯有精确的廓形打磨才能最大限度延长钢轨寿命[3]，而要实现高精度的打磨，必须深入了解钢轨廓形打磨的规律。在研究钢轨廓形打磨规律方面，日本学者岡田祐樹提出在同一打磨功率下，打磨面积是一定的，且打磨深度与打磨宽度呈负相关关系[4]；国内学者智少丹通过建立标准钢轨廓形的数学模型，提出钢轨打磨砂轮摆角越小，相同打磨面积下的打磨深度越小，但他只是简单的定性分析[5]。本文以PGM-96C型打磨车为例，对单磨头打磨的钢轨廓形进行仿真分析，将打磨砂轮与钢轨空间接触问题简化为直、曲线相交问题，基于迹线法求解打磨砂轮与钢轨的接触位置，求出打磨深度和打磨面积的关系，提出单磨头打磨量的计算方法，并通过现场试验进行验证，最后，基于岡田祐樹相同打磨功率下打磨面积相同的研究成果，定量分析当打磨功率一定时，不同打磨角度下打磨深度与打磨宽度的规律。

1 单磨头钢轨打磨量计算方法

1.1 砂轮与钢轨接触几何计算

在研究轮轨接触时广泛采用迹线法求解[6-8]，由于钢轨在纵向上可以看作是连续和对称的，本文对砂轮与钢轨接触几何计算的基本思路是将砂轮与钢轨的空间接触问题简化为横截面问题，横截面上砂轮为一条直线，钢轨廓形为一条曲线；因此可以将砂轮与钢轨的空间接触问题简化为直线与曲线的相交问题（如图1所示），再基于迹线法来求解。下面介绍具体的求解方法。

本次讨论的PGM-96C型打磨车，磨石直径254 mm，远大于钢轨横断面的宽度，在与钢轨接触前，砂轮会按照设定的打磨角度倾斜；因此，在横断面上，可以将砂轮看作一条角度确定的直线。设其打磨角度为α，则直线的斜率k=tan α。初始状态时，砂轮在钢轨上方，假设该直线在y轴的截距是h，则砂轮可以用式（1）的直线方程表示。

而钢轨由于在纵向是连续的，可以用横断面来表示，具体为式（2）所示的一个矩阵，由实测数据确定。

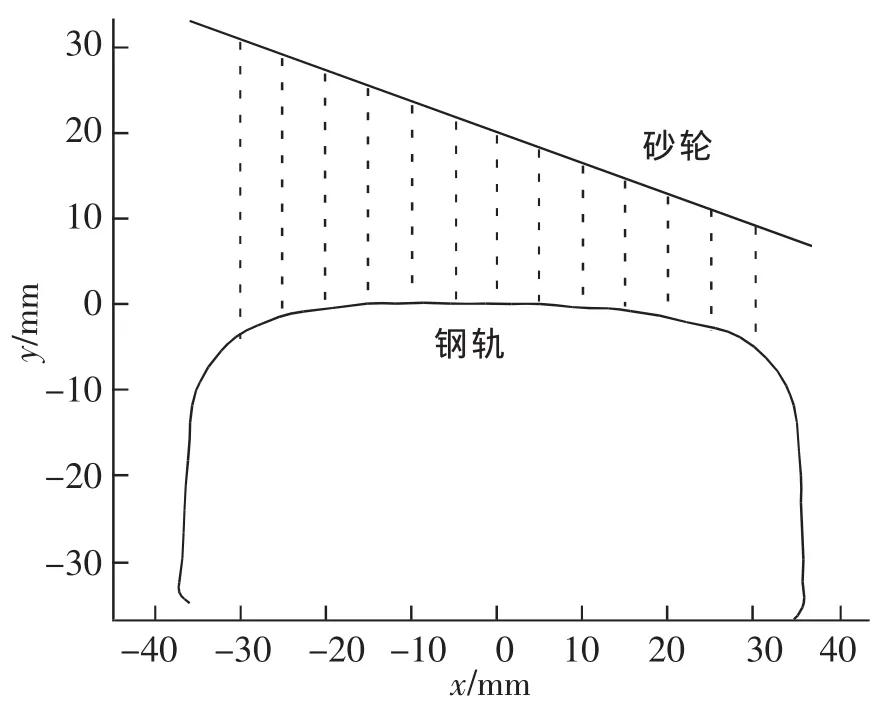
图1 砂轮与钢轨接触示意图Fig.1 Contact sketch of grinding wheel and rail

砂轮与钢轨接触时，意味着接触点处的垂向距离为0，而其它位置的垂向距离大于0。由于砂轮存在初始抬起量；因此接触点就是砂轮与钢轨垂向距离最小的点。所以，本文在x轴上搜索每个x下对应砂轮与钢轨的间隔距离。

首先，在R钢轨中找到x范围上的最小值xmin和最大值xmax，二者的定义如式（3）和式（4）所示：

之后，记循环标量为i，i从1开始，x（i）按照式（5）求取。

即以xmin开始，步长为0.01 mm，一直循环到xmax；并对每一个x值按照式（6）求得砂轮与钢轨间隔距离Δy。

当Δy取最小值时对应的x（i）即为接触点位置。

1.2 单磨头钢轨打磨量计算方法

砂轮打磨钢轨的具体流程可以分解为以下4步。

1）砂轮按照打磨角度布置好，与钢轨还没有接触。初始设定的h值较大，使得砂轮直线与钢轨横断面处于相离的状态。

2）电机将砂轮推向钢轨，砂轮与钢轨相接触。电机将砂轮推向钢轨的过程可以看作是砂轮直线平行着向钢轨靠近。用迹线法求解出砂轮与钢轨接触点位置后，接触点与砂轮初始位置的距离即是钢轨与砂轮间的最小垂向距离dmin，则与钢轨相切时，砂轮可以用式（7）所示的方程表示。

3）砂轮对钢轨进行打磨。砂轮对钢轨的打磨过程可以看作是砂轮直线从切点开始，沿着法线方向，向钢轨内侧切割。

4）砂轮打磨完成。打磨完成时，砂轮直线与钢轨横断面相交，与（2）状态时的直线平行，且间隔距离为打磨深度d打磨。此时，砂轮直线可以用式（8）所示的方程表示。

采用这种几何学等效处理方法所建立的打磨量计算模型，能通过几何学原理确定打磨深度与打磨面积之间的相互关系，利用数值方法完成求解。如图2所示，对于阴影部分的打磨面积，可以根据打磨完成后，砂轮直线与钢轨的两个交点jd1（x1，x1）和jd2（x2，x2）的坐标，再通过式（9）的积分来计算。

其中的y钢轨（x）可以用线性内插的方式求得。上述过程表明，给定了钢轨廓形和砂轮的打磨角度之后，仅需要确定一个变量——打磨深度d打磨，就能够模拟出打磨的效果，并求解砂轮与钢轨的切点坐标，交点坐标以及打磨面积等参数。

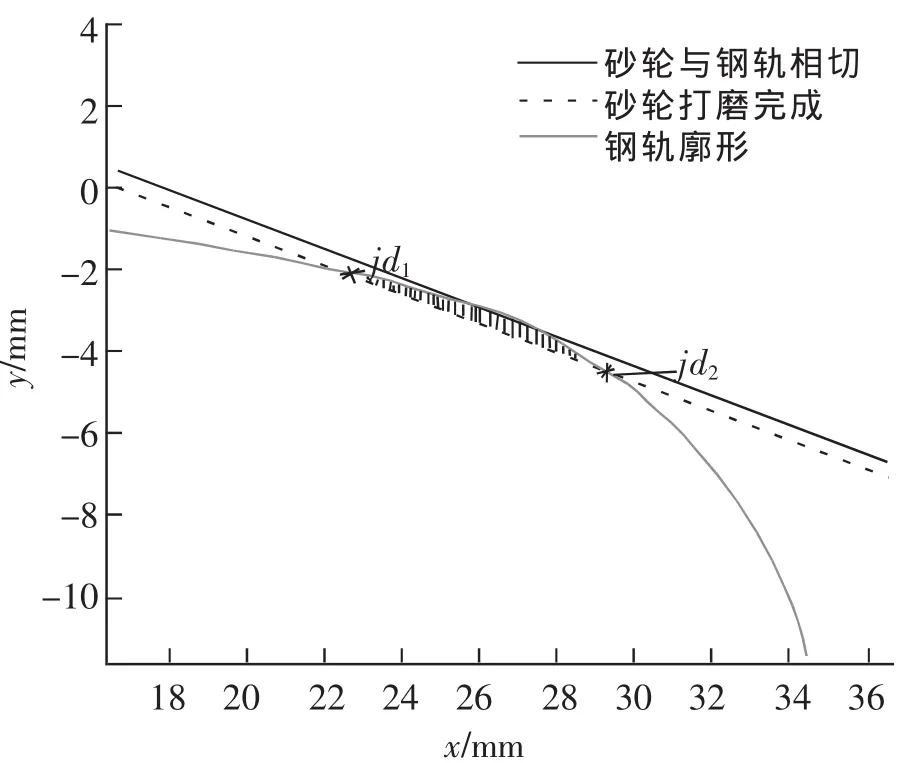
图2 打磨面积示意图Fig.2 Schematic diagram of grinding area

2 单磨头钢轨打磨量计算方法的验证

为了验证单磨头钢轨打磨量计算方法的有效性，课题组进行了现场试验。试验于2014年8月在沪昆线新桥站附近的一段直线轨道上进行，采用HTT公司的PGM-96C型96头钢轨打磨列车。试验段的左右轨分别设置了5个测点，通过MiniProf钢轨廓形检测仪采集打磨前后的钢轨廓形。

根据前期的资料调研已知，打磨角度、打磨功率和打磨速度是影响钢轨打磨量的3个主要因素。本次试验对变量进行了控制，设定打磨速度（10 km/h）和打磨功率（最大功率的80%）不变，仅研究单个砂轮条件下，打磨角度对打磨量的影响；因此，在试验时，首先控制打磨列车将所有砂轮收起，再按照表1所示的参数左右轨分别放下一个砂轮，对试验段钢轨进行打磨。

表1 现场试验打磨参数信息表Tab.1 Information table of grinding parameters in field test

对于检测到的数据，首先对齐打磨前后的钢轨廓形，钢轨廓形对齐之后可以得到实际的打磨量，打磨量分为正交坐标系下的打磨量和角度坐标系下的打磨量，二者的差别如图3所示。本次试验主要研究打磨角度对打磨量的影响；因此，选择角度坐标系下的打磨量作为分析指标，这样能更直观地反映各个角度对应的打磨深度大小。统计各个测点打磨深度超过0.05 mm的角度范围，打磨深度的最大值及其发生的位置，结果如表2和表3所示。

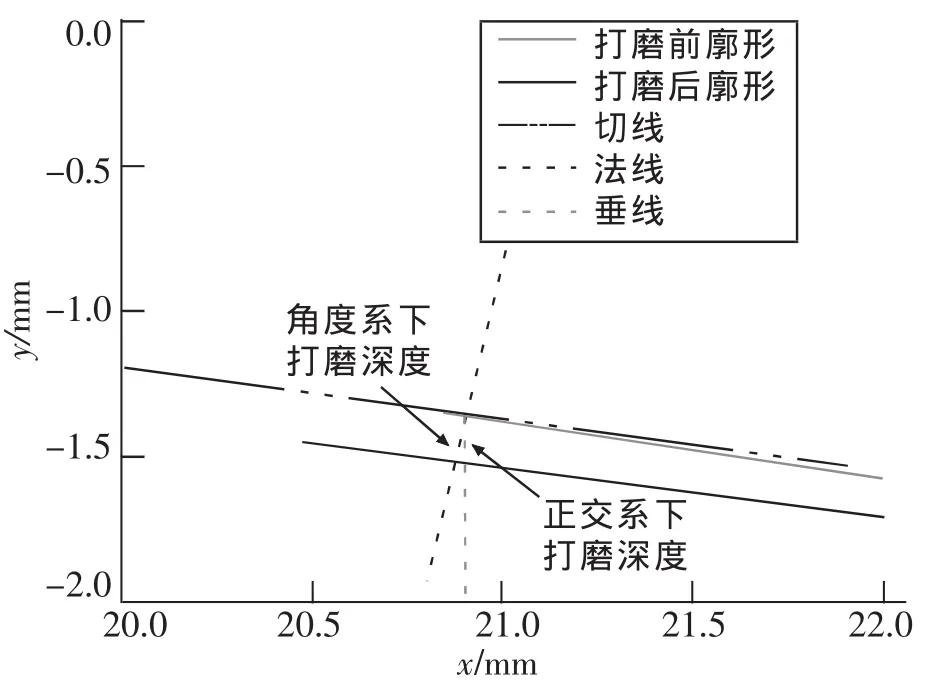
图3 不同坐标系下打磨量对比图Fig.3 Contrast of grinding quantity in different coordinate systems

结合试验所采用的打磨参数可以看出：砂轮打磨后，打磨深度的最大值基本在打磨角度位置，左轨的平均最大打磨深度为0.25 mm，右轨为0.21 mm。

为验证单磨头打磨量计算方法的正确性，将程序计算结果与实测结果进行对比，按照现场试验所采取的打磨参数，输入左轨的打磨角度为-60°，右轨为-53°，左轨的打磨深度为0.25 mm，右轨为0.21 mm。最后，将现场实测的10组打磨前钢轨廓形（左右轨各5组）输入程序，计算打磨量。部分测点程序计算与现场实测的打磨量曲线对比如图4，图5所示。

表2 左轨测点角度差异曲线特征统计表（打磨角度-60°）Tab.2 The characteristics of the rail profile in left rail(grinding angle was-60°)

表3 右轨测点角度差异曲线特征统计表（打磨角度-53°）Tab.3 The characteristics of the rail profile in right rail(grinding angle was-53°)

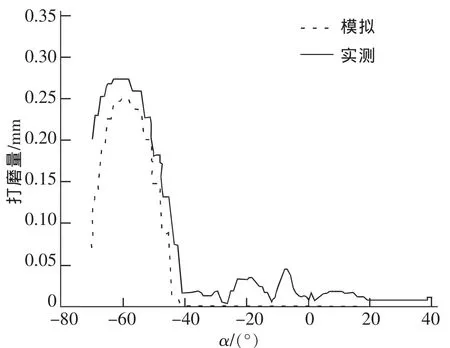
图4 左轨测点3模拟与实测角度打磨量曲线对比图Fig.4 Contrast figure of grinding quantity curve at Point 3

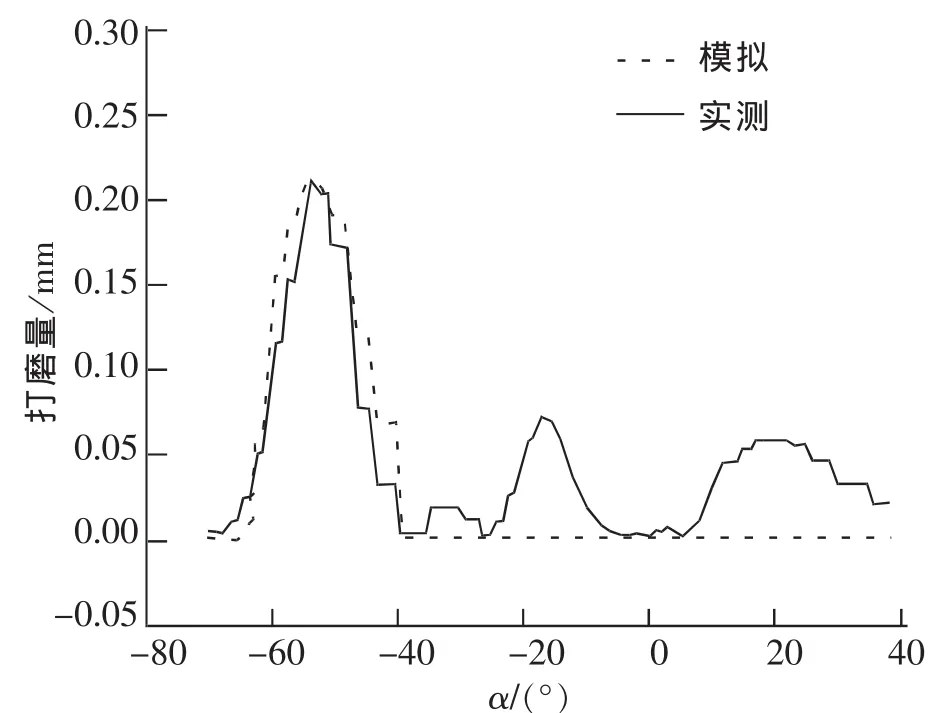
图5 右轨测点1模拟与实测角度打磨量曲线对比图Fig.5 Contrast figure of grinding quantity curve at Point 1

可以看出，程序计算的结果只在打磨角度附近有打磨量，而在其它位置打磨深度为0。而实测的打磨量曲线虽然在其它角度有打磨量，但数值很小，大多小于0.05 mm，可以看作是由检测仪器的误差造成的，程序计算和实测打磨量曲线具有较高的相似性，为分析钢轨打磨量曲线的计算结果与实测结果是否有相同的规律，对各个测点由程序计算的角度打磨量曲线进行深入分析，将程序计算的结果与实测数据进行对比，得到的结果如表4和表5所示。

表4 左轨角度打磨量曲线特征参数对比表Tab.4 Contrast of the characteristics of rail profile in left rail

表5 右轨角度打磨量曲线特征参数对比表Tab.5 Contrast of the characteristics of rail profile in right rail

可以看出，程序计算得到角度打磨量曲线平均的最大值与实测的相同，最大值发生位置也相近；除此之外，二者在打磨量大于0.05 mm的角度范围上较为接近，这说明程序计算和实测的角度打磨量曲线具有相似的规律。上述分析表明：本程序计算得到的单磨头打磨量基本可以与现场实测数据相吻合，说明本文提出的单磨头钢轨打磨量计算方法是可行的。

由于打磨面积就是打磨前后钢轨廓形之间的面积，可以通过积分的方法来求取。输入打磨参数，经程序处理，积分计算得到2次打磨的面积分别为0.693 mm2和0.641 mm2。

3 不同打磨角度下单磨头钢轨打磨廓形的仿真分析

现场试验总结出了打磨角度为-60°与-53°时的单磨头钢轨打磨量规律，并验证了单磨头钢轨打磨量计算方法的准确性，为分析不同打磨角度下的单磨头钢轨打磨量规律，现通过单磨头打磨量计算方法对不同打磨角度下的钢轨打磨廓形进行仿真分析。

根据岡田祐樹的现场总结，打磨面积由打磨功率确定。在这种情况下，当打磨功率一定时，打磨面积是固定，而打磨的角度决定了砂轮与钢轨的接触位置，通过打磨面积及砂轮与钢轨的接触位置可以反推出打磨深度，基本思路如图6所示。

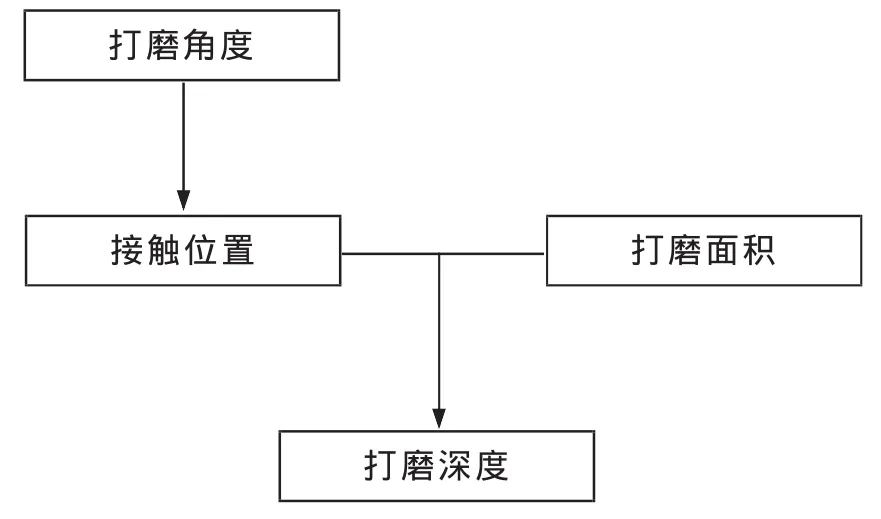
图6 打磨面积与接触位置反推打磨深度思路图Fig.6 Design of calculating grinding depth through grinding area and the contact position

现场试验的打磨功率为最大功率的80%（即17.6 kW），定义此时的打磨面积为基本打磨面积，记为S0。由现场试验结合程序计算的结果可知，打磨功率为最大功率的80%时，当打磨角度为-60°，打磨面积为0.693 mm2，当打磨角度为-53°，打磨面积为0.641 mm2，两值非常相近，与打磨功率决定打磨面积相符，取其平均值0.667 mm2作为基本打磨面积S0，要计算出某一打磨角度下的打磨深度，需综合考虑打磨面积与打磨位置，而打磨位置可通过迹线法根据打磨角度确定。

为计算出一定打磨角度下的打磨深度，引入打磨面积、接触位置反推打磨深度机制，通过循环计算某一打磨角度下一定范围内打磨深度对应的打磨面积，并与S0匹配得到其对应的打磨深度dα，完成打磨量的计算。首先，模型可以根据打磨角度和打磨前廓形，通过迹线法确定砂轮与钢轨的接触位置；之后，选择打磨面积作为计算指标，以打磨深度d为基本变量，在一定的范围内递增，并不断计算对应打磨面积的大小。记循环序号为j，则可以根据打磨深度d（j）求得砂轮打磨后与钢轨廓形的2个交点坐标jd1（x1，x1）和jd2（x2，x2），通过式（10）积分求得打磨面积。

最后，将每次模拟得到的Sj与基本打磨面积S0进行对比，当二者的差异最小时，即可匹配求得打磨角度为α时对应的打磨深度dα，其流程如图7所示。

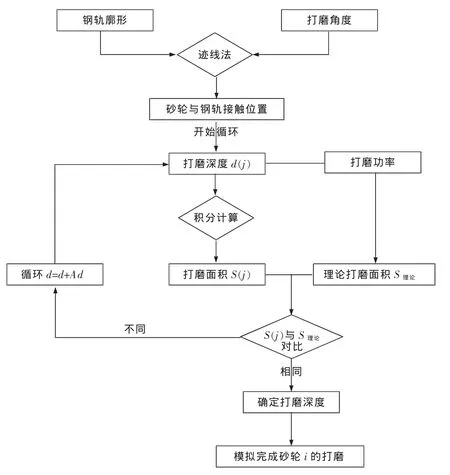
图7 打磨面积反推打磨深度流程图Fig.7 The flow chart of calculating grinding depth through grinding area

通过单磨头钢轨打磨量的计算程序，可以分析出不同打磨角度对应的打磨量规律。采用标准60轨廓形，针对目前常用的打磨角度范围-60°至30°，通过程序计算不同打磨角度下的打磨量，得到的砂轮与钢轨接触位置如图8所示，而打磨量规律如表6所示。

可以看出，随着打磨角度的增大，砂轮与钢轨的接触点以及打磨完成后砂轮与钢轨的交点坐标均逐渐由轨距角向非工作边移动，可见，打磨角度决定了砂轮与钢轨的接触点位置。相同打磨功率下，砂轮摆角越小，打磨深度越小，打磨宽度越大，即当砂轮与钢轨的接触点在轨顶时，打磨深度最小，打磨宽度最大，随着接触点向两侧移动，打磨深度逐渐增大，打磨宽度逐渐减小。

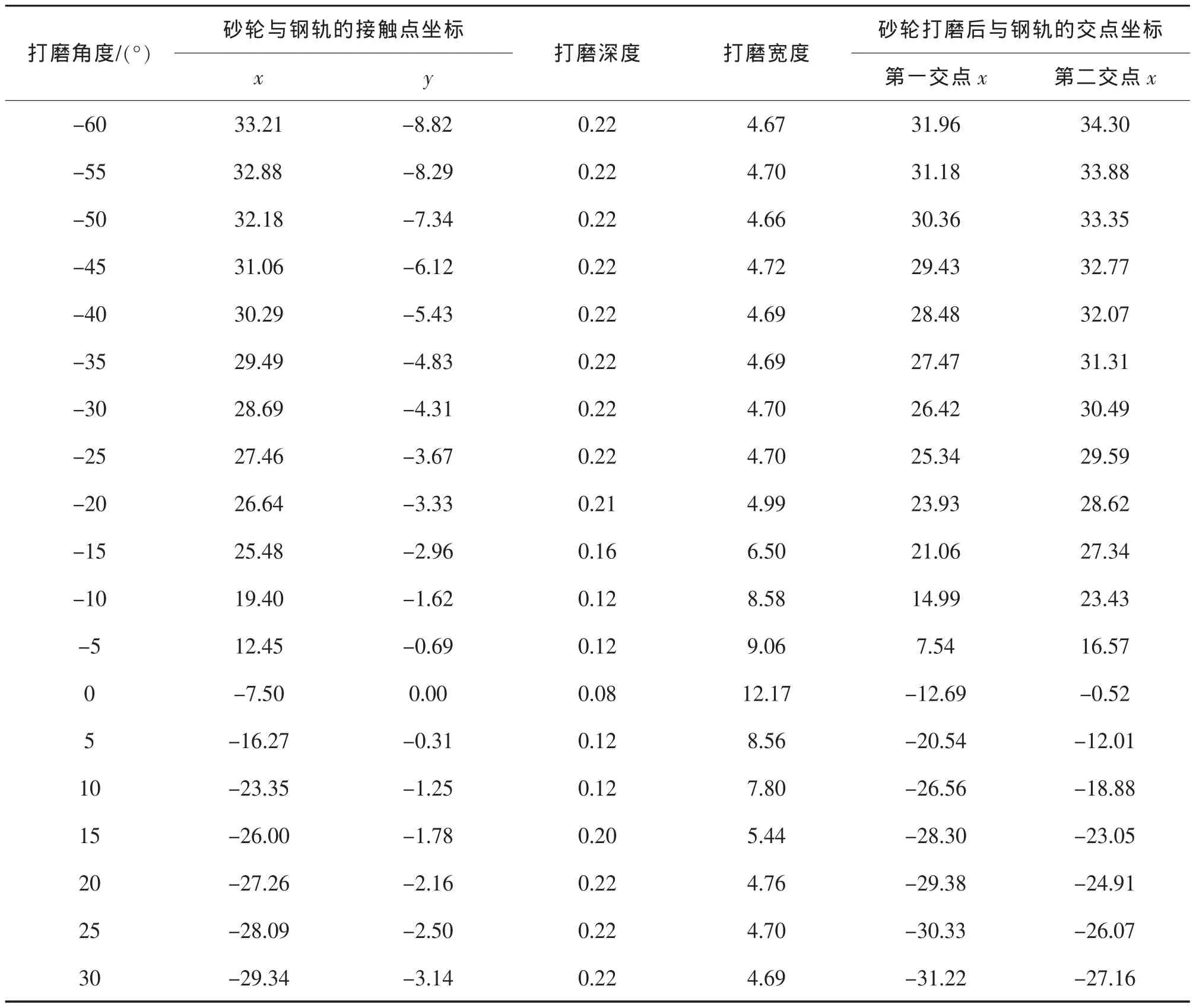
表6 单磨头不同角度打磨量规律统计表Tab.6 Information of rail profiles in different grinding angles mm

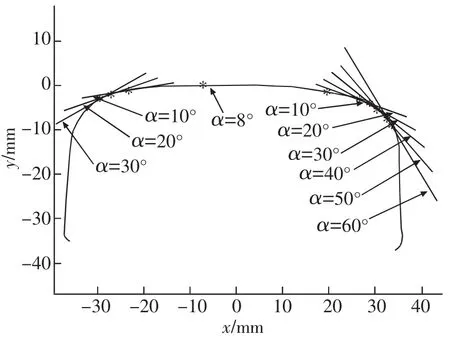
图8 不同角度砂轮与钢轨接触位置示意图Fig.8 Schematic diagram of the contact position between grinding wheel and rail in different angles

4 结论

提出单磨头打磨量的计算方法，并通过现场试验进行验证，通过该计算方法对不同打磨角度下单磨头打磨钢轨廓形进行仿真分析，得出的结论如下。

1）基于迹线法求解砂轮与钢轨的接触位置，通过打磨深度积分计算打磨面积，提出单磨头打磨量的计算方法，并通过现场试验进行验证，得到的结果与现场实测数据较为吻合，通过该计算方法进行的单磨头打磨钢轨廓形仿真分析，可以满足现场需求。

2）通过对PGM-96C型打磨车不同打磨角度下的单磨头打磨钢轨廓形的仿真分析发现，在17.6 kW的打磨功率下，砂轮摆角为0°时，钢轨打磨深度为0.08 mm，打磨宽度为12.17 mm，随着砂轮摆角增大，钢轨打磨深度增大，而打磨宽度减小，砂轮摆角增大到20°以上时，打磨深度维持在0.22 mm左右，打磨宽度维持在4.70 mm左右。

[1]金学松，杜星，郭俊，等.钢轨打磨技术研究进展[J].西南交通大学学报，2010，45(1)：1-11.

[2]李再帏，练松良，李秋玲，等.城市轨道交通轨道不平顺谱分析[J].华东交通大学学报，2011，28（5）：83-87.

[3]杜星，基于轮轨几何特征的钢轨打磨应用研究[D].成都：西南交通大学，2011.

[4]MAGEL EE，KALOUSEK J.The application of contact mechanics of rail profile design and rail grinding[J].Wear，2002，253（1/2）：308-316.

[5]罗文俊，雷晓燕，练松良.车辆-高架桥耦合系统竖向振动分析车辆轨道新模型[J].华东交通大学学报，2013，30（2）：1-8.

[6]岡田祐樹，武井昭洋.山阳新干线轨道削正作业的验证[C]//土木学会第60次学术研讨会，2005.

[7]智少丹，李建勇，蔡永林，等.基于标准廓形钢轨的打磨模式机理[J].中南大学学报：自然科学版，2015（6）：2027-2035.

[8]王璐颖.钢轨打磨车抗脱轨稳定性研究[D].成都：西南交通大学，2012.

[9]SATOH Y,IWAFUCHI K.Effect of rail grinding on rolling contact fatigue in railway rail used in conventional line in Japan[J]. Wear，2008，265（9/10）：1342-1348.

[10]GRASSIE SL.Rolling contact fatigue on the British railway system:treatment[J].Wear，2005，258（7/8）：1310-1318.

Simulation Analysis of the Rail Profile after Grinding by Single Grinding Wheel

Qiu Junxing1,Xu Yude1，Lu Ye2，Sheng Jianfeng1,Li Fengyu1
（1.Key Laboratory of Road and Traffic Engineering of the Ministry of Education,Tongji University,Shanghai 201804,China；2.China Railway Eryuan Engineering Group CO.,LTD.,Chengdu 610031,China）

Rail grinding is an important means for railway maintenance,and only grinding with high precision can further prolong the service life of rail.Hence,it is significant to research the rail profile after grinding for improving the grinding accuracy.This paper,taking the PGM-96C grinding car as an example,proposed a grind ing quantity calculation method of single grinding wheel,then verified the calculation method by field test,and finally made the simulation analysis of rail profiles in different grinding angles.Results show:when the grinding power is 17.6 kW and the angle of grinding wheel 0°,the grinding depth is 0.08 mm and the grinding width is 12.17 mm；with the increase of the angle,the grinding depth is also increasing,but the grinding width is decreasing;when the angle of grinding wheel is more than 20°,the grinding depth remains around 0.22 mm with the grinding width around 4.70 mm.

rail grinding;single grinding wheel;simulation analysis;grinding angle

U216

：A

1005-0523（2017）01-0099-08

（责任编辑 刘棉玲）

2016－09－16

国家自然科学基金项目（50908179）；上海市自然科学基金项目（11ZR1439200）

邱俊兴（1993—），男，硕士研究生，研究方向为铁道工程。

许玉德（1965—），男，教授，工学博士，博士生导师，主要研究方向为轨道管理，轨道养修技术。