公路隧道照明灯具利用系数研究

杨 超，程 翠

(华东交通大学机电与车辆工程学院, 江西 南昌 330013)

公路隧道照明灯具利用系数研究

杨 超，程 翠

(华东交通大学机电与车辆工程学院, 江西 南昌 330013)

灯具利用系数是隧道照明设计、参数优化中计算路面水平照度的一个重要参数，提高灯具利用系数有利于提高路面的平均照度。但目前使用该参数时，多数采用灯具利用系数曲线或设为定值，造成计算误差。为了得到能根据灯具配光数据和布灯参数变化的利用系数，建立了隧道照明灯具利用系数计算模型，并依据此模型，分析了利用系数与布灯高度、布灯横向偏移距离及布灯仰角的变化规律。仿真算例表明，所建利用系数模型正确，用于布灯参数优化时，比利用系数取定值时的结果更准确，照明系统也更节能。此模型适用于中央布灯、拱顶侧偏布灯、交错布灯和对称布灯形式灯具利用系数的计算。

隧道照明；利用系数；布灯参数

引言

灯具利用系数是指工作面或规定的参考平面上，直接或经相互反射接收的光通量与照明装置全部灯具发射的额定光通量总和之比，是灯具效率、灯具光强分布、空间几何特征和空间结构表面反射系数的函数，是照明设计的一个重要指标。《公路隧道照明设计细则》(JTG/J D70/2-01—2014)给出了采用灯具利用系数曲线图计算隧道路面平均水平照度的方法[1]，但计算精度不高；文献[1]没有给出灯具布灯参数发生变化时的计算方法。季佳俊[2]仿真研究了LED灯与高压钠灯不同布灯形式、不同高度、不同间距对灯具利用系数的影响规律；韩文元等[3]在固定灯具安装高度、横向安装距离和安装仰角的情况下，对20种不同的公路隧道照明灯具的利用系数进行了测试，得出了公路隧道照明灯具利用系数的取值范围。在隧道照明优化设计过程中，当灯具配光曲线、灯具布置参数发生变化时，文献[2-3]给出的方法均无法应用。为了简化计算，国内隧道照明设计和布灯参数优化研究中，通常直接根据灯具的利用系数曲线[4]或取灯具利用系数为某一固定值[5-7]进行计算，带来设计、计算上的误差。更多的隧道照明节能研究文献则避开灯具利用系数。

在隧道照明优化设计中，为了能够根据灯具配光曲线和布置参数实时调整灯具利用系数，本文将建立基于隧道照明灯具的配光数据和布灯参数的利用系数模型，研究其与灯具安装高度、横向安装距离、安装仰角的关系，并进行优化仿真验证。

1 单个灯具利用系数

计算隧道路面水平照度时，路面的有效光通量等于灯具利用系数η0与照明灯具发射的额定光通量之积。对于同一个系列的灯具，往往具有相同或相近形状的配光曲线。

1.1 隧道路面的有效光通量

当灯具的类型、安装高度、安装仰角、隧道路面宽度、隧道墙壁材料的反光系数[8-9]等发生变化时，路面的有效光通量也会发生变化。隧道照明灯多为方口灯，假设其投射到地面的照明区域亦为四边形(或近似四边形)。图1所示为隧道照明布灯的横截面示意图。图中，d为隧道路面的宽度(m)；d1为灯具中心到路面中心线的水平距离(偏移距离，m)；A表示灯具中心位置；AO为灯具垂线；AO1为灯具光轴线；ξ为灯具在Y方向的仰角(rad)；B和C分别为隧道侧壁与路面的交点位置；D和E分别为隧道侧壁上距离地面2 m高的位置；Y方向为隧道横向，Z方向为隧道高度方向。只考虑一次反射，则一个灯具在隧道路面产生的有效光通量Φe(lm)由灯具直接照射到路面的光通量Φd(lm)和经隧道墙壁反射的光通量Φf(lm)组成，即Φe=Φd+Φf。Φf包括隧道侧壁高度2 m以内光通量的反射量和2 m以外光通量的反射量。

图1 灯具照明布灯横截面示意图Fig.1 Cross-section diagram of tunnel luminaire distribution

图2为隧道布灯立体角计算图，其中，X方向为隧道纵向，θ为水平角(rad)，γ为垂直角(rad)。BC和DE分别为隧道侧壁与路面相交线，BCDE为灯具射出的光线在隧道路面上形成的照明区域；B′C′和D′E′分别为隧道侧壁2 m高处与灯具光线的相交线，B′、C′、D′、E′分别为灯具以发光角射出的光线与B′C′和D′E′的交点；γ1和γ3分别为灯具投射到BC和B′C′上的光线AF和AF′与光轴线AO1的夹角；γ2和γ4分别为灯具投射到DE和D′E′上的光线AG和AG′与光轴线AO1的夹角(图中未标出)；θ11和θ12分别为灯具仰角方向的光线投射到C、B点时在配光剖面C0/180(θ=0)两侧形成的水平角；θ21和θ22分别为灯具仰角反方向的光线投射到D、E点时在配光剖面C0/180(θ=π)两侧形成的水平角；θ31和θ32分别为灯具仰角方向的光线投射到C′、B′点时在配光剖面C0/180(θ=0)两侧形成的水平角；θ41和θ42分别为灯具仰角反方向的光线投射到D′、E′点时在配光剖面C0/180(θ=π)两侧形成的水平角。

图2 隧道布灯立体角计算图Fig.2 Solid angle calculaticn diagram of tunnel luminaire distribution

根据文献[10]，结合图1和图2，可得利用灯具配光曲线计算光通量的表达式。

1) 灯具产生的总光通量Φ(lm)为

2) 灯具照射到隧道侧壁上光通量Φ1(lm)为

3) 灯具照射到隧道2 m以上侧壁上的光通量Φ2(lm)为

式(1)～(3)中，Ic(γ,θ)为灯具在水平角为θ和垂直角为γ处的光强(cd)；γ1～γ4分别按式(4)～(7)计算；θ11～θ42分别按式(8)～(15)计算。

式中，h为灯具安装高度(m)；h′=h-2；K1=d/2+d1，K2=d/2-d1；α1、α2分别为灯具在X方向和-X方向的发光角度(rad)。

灯具直接照射到隧道路面的光通量为Φd=Φ-Φ1，灯具照射到隧道侧壁2m以内墙面的光通量为ΔΦ1=Φ1-Φ2。设隧道侧壁2m以内部分的墙壁反光系数为ρ1，2 m以外部分的墙壁反光系数为ρ2，则一个灯具在路面产生的有效光通量为

式(1)～(16)不适用于逆光照明的计算。

1.2 单个灯具利用系数

根据灯具利用系数的定义得

可以看出，灯具的利用系数与灯具的配光曲线、布灯参数有关，不宜设为固定值。

2 多个灯具的利用系数

假设多个灯具纵向安装间距、安装高度、横向偏移距离、安装仰角、灯具型号、功率均相同，在隧道某个区域内安装了N个灯具，区域两端的灯具光通量有一部分投射到区域之外；只考虑区域两端的灯具投射到区域之外的光通量损失，则有

对于中央布灯、拱顶侧偏布灯和交错布灯形式，k=1；对于两侧对称布灯形式，k=2。当研究区域为隧道中某两个纵向相邻的灯具之间的路面区域时，可取一个灯具的利用系数η0,1作为研究区域路面上的利用系数η0。

3 布灯参数对利用系数的影响

3.1 算例隧道

以江西九景高速公路雁列山隧道作为研究对象[11]，该隧道为双洞单向交通设计，由1号、2号两座隧道构成，全长3 352 m，其中1号隧道长1 533 m，2号隧道长1819 m，隧道路宽10.25 m，净高7.425 m，行车道宽8.5 m，设有人行检修道，设计交通量(1 200辆/h，设计车速80 km/h。以2号隧道为例，其隧道中间段长度约为1 383 m。参照文献[7]，隧道墙面2 m高范围内铺设反光系数为0.86的材料，即ρ1=0.86，其余部分为水泥混凝土面，反光系数为0.24～0.31[2]，本文取0.275，即ρ2=0.275。

3.2 灯具选择

采用雷士照明LED灯系列，灯具型号为NHLED101～NHLED103，α1=α2=π/3，发光效率为100 lm/W，配光曲线形状见文献[7]。

3.3 利用系数与布灯参数的关系

1) 中央布灯形式。根据文献[7]，取N=156，灯具安装高度h的变化范围为4.5 m～7 m。利用公式(18)可得照明系统的利用系数随高度h的变化情况如图3所示。可以看到，安装高度为4.5 m时，利用系数为0.942，随着灯具安装高度的增大，照明系统的利用系数减小，从提高灯具光通量利用系数的角度来看，灯具的安装不宜过高。图3中还给出了ρ1=0.782时照明系统的利用系数。当反光材料的反光系数从0.782提高到0.86时(提高幅度10%)，利用系数的提高幅度在0.745%～1.183%之间。可见，采用高反射率材料有助于提高隧道侧壁的亮度，但提高利用系数的效果不显著。

图3 中央布灯η0与h的关系Fig.3 Relationship between η0 and h of central luminaire distribution

2) 拱顶侧偏布灯形式。取N=156，灯具安装高度h的取值范围为4.5 m～6 m，灯具偏移隧道中心线的距离(侧偏距离)d1=0～2 m，灯具安装仰角0～30°。利用公式(18)可得利用系数随h、d1和ξ的变化情况。图4所示为灯具安装高度固定为6 m时，利用系数随d1和ξ的变化情况。从图4可以看到，安装高度固定时，不同的侧偏距离，对应最大利用系数的灯具安装仰角不同；d1=0时，对应最大利用系数的安装仰角也为0。

图4 h=6 m时η0随d1和ξ的变化情况Fig.4 Changing of η0 with d1 and ξ while h=6 m

图5所示为侧偏距离固定为1 m，安装高度取4.5 m～6 m时利用系数随灯具安装仰角的变化情况。可以看出，当灯具安装偏离路面中心线时，一定要有安装仰角，适宜的安装仰角可提高灯具利用系数。

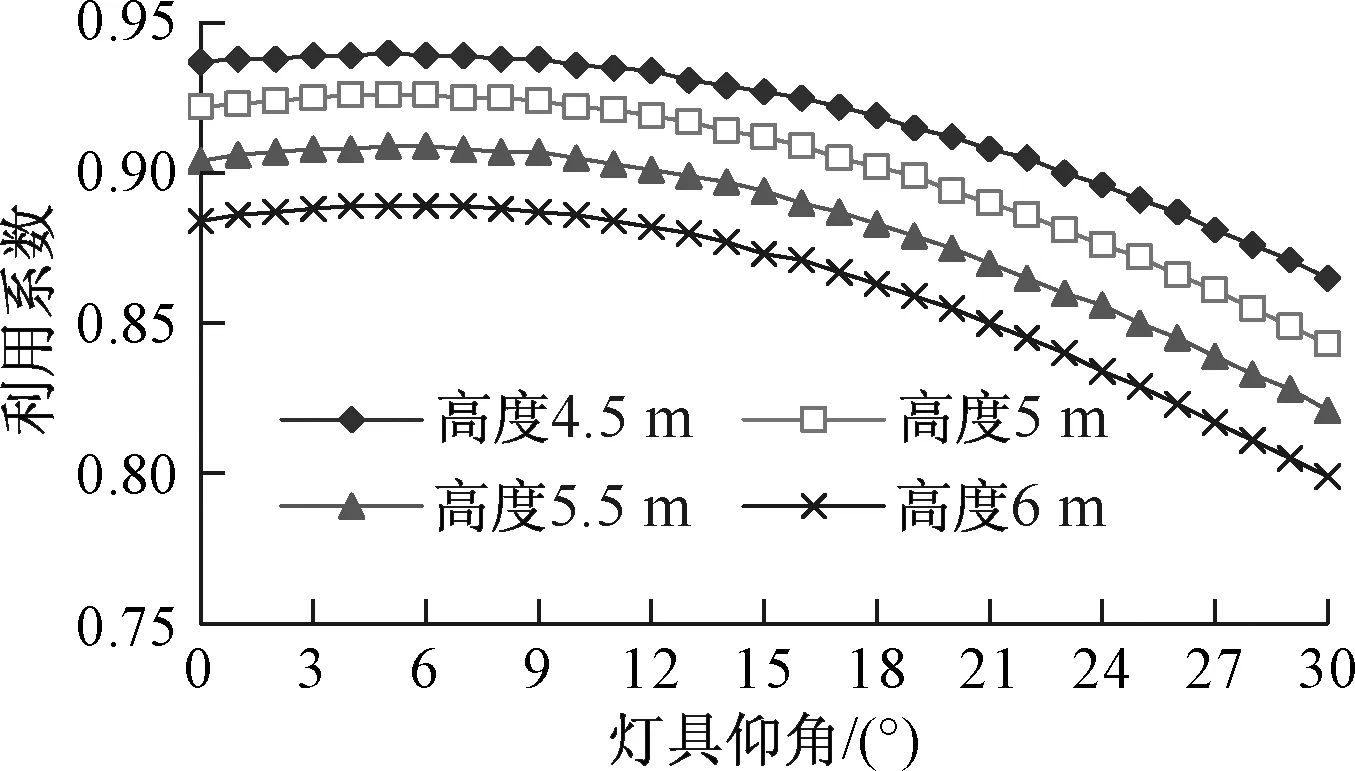
图5 d1=1 m时η0随h和ξ变化的情况Fig.5 Changing of η0 with h and ξ while d1=1 m

两侧交错布灯和两侧对称布灯形式，都可以根据侧偏布灯形式进行分析。不论何种布灯形式，只要布灯参数、灯具配光曲线以及隧道侧壁和路面反光系数发生变化，其利用系数都会变化。灯具利用系数对照明系统的能耗有影响，提高灯具利用系数可以提高照射到路面的光通量。但是，不能忽视提高灯具利用系数对其它参数的影响，例如，采用中央布灯方式，其它参数保持不变，降低灯具安装高度可以提高灯具利用系数，但路面最小照度和照度均匀度会降低，对隧道侧壁2 m高范围内的平均亮度也有影响。因此，在进行布灯参数优化时，需要根据隧道照明要求，确定最佳布灯参数和最佳利用系数。

3.4 布灯参数及利用系数优化算例

采用NHLED101～NHLED103雷士照明LED灯，以江西九景高速公路雁列山隧道作为研究对象。因最小照度区域通常位于隧道路面两边，以49.5lx≤最小照度≤50.5lx为优化条件，对行车安全不会造成影响；无光衰时参数优化结果、照明效果仿真结果及总功耗如表1所示。

表1 布灯参数及利用系数优化结果、照明效果及总功耗Table 1 Optimized parameters of luminaire distribution, utilization factor, lighting offects and total power consumption

从表1可以看出，即使采用的灯具相同，但布灯方式不同，利用系数η0也不是固定值，而是与布灯参数有关。从照明效果仿真值可以看到，都符合隧道交通照明要求，表明布灯参数优化结果和本文建立的利用系数模型是正确有效的。在文献[7]中，几种布灯方式下的最优布灯参数，均是取η0=0.85求得的。本文将布灯参数和利用系数一起优化，优化后的布灯参数与文献[7]不同；相比文献[7]，本文优化后的照明系统更节能，总功耗更小，中央布灯、拱顶侧偏布灯、对称布灯和交错布灯，分别节能7.74%、10.26%、10.63%和0.69%。

不同的照明灯具，其配光曲线可能不同，当照明灯具或布灯方式变化时，其最优布灯参数和利用系数也会变化，所以，需要进行较精确的优化计算时，利用系数不宜设为定值。

4 结束语

本文根据隧道照明的灯具配光曲线、布灯参数及隧道横截面结构尺寸，建立了隧道照明单灯利用系数和照明系统利用系数计算模型，解决了现行隧道照明设计、优化过程中采用灯具利用系数曲线或将利用系数曲线设定为定值造成计算误差的问题。利用所建灯具利用系数模型，分析了利用系数与布灯高度、布灯横向偏移距离及布灯仰角的变化情况，分析了利用系数最大的灯具仰角与布灯横向偏移距离及布灯高度的变化情况，即最大利用系数对应的灯具仰角随布灯横向偏移距离的增大而增大，随布灯高度的增大而增大。在进行照明系统较精确的优化设计时，应根据灯具配光曲线优化布灯参数和确定利用系数，不宜将利用系数设为定值。

[1] 公路隧道照明设计细则: JTG/J D70/2-01—2014[S]. 北京:人民交通出版社, 2014.

[2] 季佳俊. 三车道大断面公路隧道照明节能参数优化研究[D].重庆: 重庆交通大学, 2012.

[3] 韩文元,殷杰,杨勇，等.公路隧道照明灯具有效能效指标分析[J].公路交通科技, 2015, 32(11): 94-99.

[4] 涂钢.公路隧道照明优化设计方法及软件开发[D].西安:长安大学，2015.

[5] YANG Chao, HUANG ChuanMao, FAN ShiJuan. Study on Energy Saving of Symmetrical Luminaire Distribution Style of Highway Tunnel Lighting[C]//The 2015 International Conference on Mechanics, Building Material and Civil Engineering (MBMCE 2015). Guilin, 2015.

[6] FAN Shijuan, YANG Chao.Parameters Optimization and Energy-saving of Highway Tunnel Stagger Luminaire Distribution Lighting with LED[C]//International Conference on Civil, Transportation and Environment (ICCTE 2016). Guangzhou, 2016.

[7] 黄传茂. 高速公路隧道照明系统布灯参数优化研究[D].南昌：华东交通大学，2016.

[8] 杨韬,陈仲林.隧道照明反射增量系数研究[J].灯与照明, 2009, 33(2):6-14.

[9] 潘国兵,梁波,皮宇航,等.隧道侧壁内装材料的照明节能[J].公路交通科技, 2012, 29(9):103-109.

[10] 张九红,庄金迅.配光曲线在照明计算中的应用[J].沈阳建筑大学学报(自然科学版), 2007, 23(6): 941-944.

[11] 何凌坚,李世京.九景公路雁列山隧道复合式衬砌防排水的设计与施工[J].探矿工程, 1999, 6: 39-41.

Study of Utilization Factor of Highway Tunnel Luminaire

YANG Chao, CHENG Cui

(SchoolofMechatronics&VehicleEngineering,EastChinaJiaotongUniversity,Nanchang330013,China)

Utilization factor (UF) of luminaire is an important parameter in calculating horizontal illuminance of tunnel road surface in the process of tunnel lighting design or parameters optimization of tunnel lighting, increase of UF is conducive to the average illuminance of road surface. However, UF was usually set as a fixed value or get from UF curve of luminaire, which caused calculation errors. An UF model of tunnel lighting luminaire was made to get the real UF in accordance with light distribution data of adopted luminaire and luminaire installation parameters. Based on the model, the relationships between UF and luminaire installation height, crosswise offset distance and elevation angle were analyzed. A simulation example showed that the UF model is correct, when the UF model is applied to optimization of luminaire installation parameters, more accurate optimized parameters and more energy-saving lighting system can be gotten than that of UF set as a fixed value. The UF model is suitable for calculation of UFs of central luminaire distribution, offset-of-vault luminaire distribution, stagger luminaire distribution and symmetric luminaire distribution.

tunnel lighting; utilization factor; luminaire installation parameters

国家自然科学基金项目资助(项目编号：61463015)

TM923

A

10.3969/j.issn.1004-440X.2017.01.017