婴儿潮对住房价格的影响——从人口结构变动的角度出发

王璞

（香港科技大学数学系，香港999077）

婴儿潮对住房价格的影响
——从人口结构变动的角度出发

王璞

（香港科技大学数学系，香港999077）

“婴儿潮”带来的人口结构的变动对住房价格的影响不仅体现在特定年龄段居民绝对数量的变化，也体现在其相对数量的变化。这些因素与该地区的住房总需求息息相关，最终对住房价格产生影响。在实证分析中，使用总人口和老年人口抚养比例两个指标，并预期前者对住房价格有积极影响而后者则相反进行实证分析，带有时间虚拟变量的随机效应模型的回归结果表明：在美国，人口结构结构变量都对住房价格有着显著的影响，并且符合预期。但在中国，老年人口抚养比对住房价格影响为正，且在统计上不显著。

婴儿潮；人口结构；老年人口抚养比；住房价格；代际交叠模型；随机效应模型

一、引言

与相邻时间段相比，在某一特定时段内出生的人口数量较大，即人口自然生长率较高，这样的现象被称为“婴儿潮”。中美两国自20世纪50年代以来都出现过人口数量增长的现象（见图1，图2）。人口数量及结构变化所产生的经济影响不仅在那一特定时间段内，更存在于之后的数十年。当婴儿潮一代逐渐步入工作年龄，整个社会的工作人口增加，带来了“人口红利”。毋庸置疑，这为经济的迅速发展提供不断扩大的劳动市场和消费市场。但是，当这一代人渐渐老去，在缺乏大量青年人口移民的情况下，随之而来的极可能是加速的人口老龄化。这又会对一个社会的经济产生怎样的影响呢？

如果将目光仅仅聚焦于住房市场，婴儿潮引发的数十年的人口结构变动是否对住房价格产生了影响？本文利用美国和中国的地区面板数据，通过理论模型的推导和实证模型的回归分析方法对此问题做出肯定的回答。更进一步，当知晓这一影响的存在，是否可以对一地区的住房价格做出符合其过去发展经历和经济学逻辑的未来趋势的判断呢？本文将在最后根据全文的分析和预测的人口结构发展方向对此得出定性的结论。

在实证分析中需要注意的一点是，中国1998年才开始住房市场化改革，2000年之后其住房市场才渐渐完善。［1］在这段时间内，住房市场化之前积压的一代人与80十年代的婴儿潮一代的住房需求共同爆发出来。因此本文的实证分析加入美国地区面板数据，借此得出更加一般化的结论。

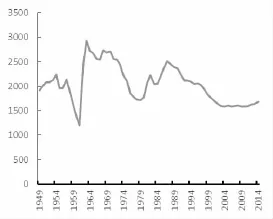
图1 中国历年出生人口（万人）

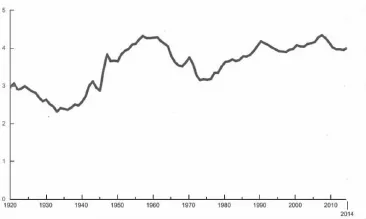
图2 美国历年出生人口（百万人）

Mankiw＆amp;Weil（以下简称MW）最先通过“婴儿潮”来考察人口结构的变动对住房市场的影响。他们预测随着美国二战后婴儿潮一代（出生于1946年～1964年间）的年龄增长，到90年代美国的住房需求会增长缓慢，而住房价格则在接下来的二十年下降47％。［2］但是，仍有不少学者从实证和理论的角度对MW的研究成果提出质疑。例如，Hamilton尝试用租金取代了M-W模型中的住房价格，重新回归后发现租金与住房需求呈反向关系，而美国的实际资产价格与租金变动率成反向关系。［3］Green和Hendershott利用美国1980年数据分析年龄结构、教育程度和收入水平对住房需求的影响，发现在控制其他变量不变之后，住房需求随着年龄的增加变得平稳甚至轻微的上升。［4］

有不少中国学者借鉴国外的研究成果，从研究影响中国城市住房需求的人口结构因素出发，展开了对中国住房市场的研究。陈斌开等最先做出了这方面的基础研究。他们利用中国人口普查数据和M-W模型推断出中国的个人住房需求与年龄的关系曲线，指出了个人的住房需求从20岁开始迅速上升，到50岁后开始逐步下降。这表明新生儿主要影响到20年后的住房市场。最后，他预测人口老龄化将导致住房需求的增长率在2012年后大幅下降，住房价格将因此面临下行压力。［5］然而，陈彦斌等对此结论做出了反驳。充分考虑城镇化、家庭规模小型化和人口老龄化（人口年龄结构变化）三个因素的动态影响之后，他们用家庭数量和年龄构成的变化来估算的住房需求变化的数据表明：人口老龄化对城市住房需求的负面冲击在2045年以前可能不会显现出来。［6］

得益于国外的研究经验，中国的学者们在短时间内获得了颇为丰富的研究成果。这样的进步使得学者们在分析中国住房价格不断上升的现状时不再局限于以前的角度，从而更有利于认识这一现象产生的本质原因。

二、理论模型

（一）Takats模型

Takats根据生命周期理论，构建了一个简单的代际交叠模型来考察人口结构对住房价格的影响。［7］本文将先简单介绍该模型，并在下一节分析这一模型对实证研究的启示，并在第三小节基于Takats模型，结合供给市场的实际情况，扩展该模型。

1.模型假设

首先，假定代表性行为人只生活两期：青年时期和老年时期。青年行为人工作并获得外生的工作收入，同时，他们还需要进行储蓄以供老年时期的消费。进一步，我们假定储蓄通过在住房市场买卖房屋来完成。代表性行为人符合理性人假设，目标为最大化两期消费效用。他们的效用函数（U）为：

这里，cY为青年时期的消费，c0为老年时期的消费，β为贴现因子。

接下来引入住房市场。假设可供行为人交易的住房资产是可分，在时期t价格为Pt，总量为K且不变。因为行为人都是同质的，并且均衡状态下住房的累积产出等于累积消费。所以在均衡时，青年人的个人储蓄等于住房资产总价值（PtK）除以当时的青年人口总数（ntY）。因此，在t时期行为人的约束条件为：

然后在t+1期，老年行为人以Pt+1价格卖掉自己的房屋，并以此消费：

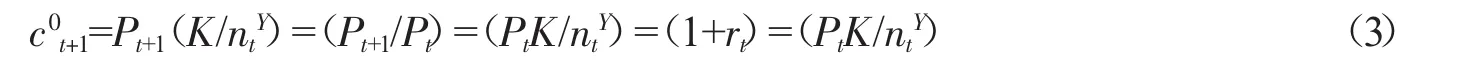
（3）式表明行为人老年时期的消费取决于初始的储蓄（PtK/ntY）和储蓄的收益率（1+rt）。

在对模型进行均衡分析前，需要定义两个概念。首先，定义人口结构变动指标（dt）为：

其次，定义外生的经济增长率为：

2.均衡分析

这一模型的均衡结果是显而易见的。首先，根据代表性行为人的效用函数和预算约束条件可以得出行为人青年时期的最优消费为：

至此，根据（2）式可以得到t期个人储蓄-住房投资的均衡方程：

由t+1期和t期的储蓄-住房投资均衡方程相除可以得到住房价格的演变路径：

（8）式表明：如果青年人口更富有或者更多，那么住房价格将会上涨。因为这种情况中，下一代会产生更多的住房需求。当然这样的结论与住房供给保持不变的假设有很大的关系。

（二）模型含义

总而言之，经济增长和人口结构因素驱动着住房价格。这一模型能够用来指导实证研究时解释变量的选择。虽然它用到了很多简化问题的假设，例如，住房供给保持不变，又或者老年户主卖掉自己的房屋来进行消费等。在实际情况中，这些情况可能更加复杂和丰富。但是，正是这样简化的思考方式，能够在选择实证模型变量时提供关键的指引。

（8）式的真实经济增长率（1+g）可以用真实人均GDP（简记为：perGDP）增长率来表示。这也表明：当居民越富有时，他们越愿意购买新的住房。

（8）式的人口结构变动指标（1+d）可以通过总人口（简记为：TPOP）增长率和老年人口抚养比（简记为：OLDDEP）的导数来表示。老年人口抚养比，即老年人口（65岁以上）对工作人口（20岁到64岁）的比值，可以看作该模型中青年人口（nt）对老年人口（nt-1）的比值。所以，能得出下式：

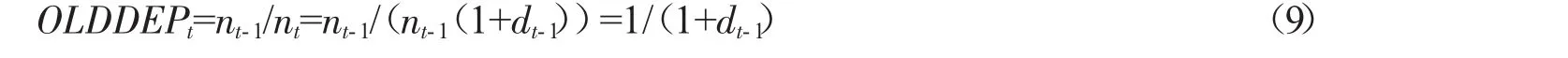
这两个人口结构指标（TPOP、OLDDEP）对实证分析都有不可忽视的作用。一方面，TPOP衡量了人口规模的大小；另一方面，OLPPEP显示了人口年龄结构的影响。通过实际数据可以发现两者的相关性并不大（相关系数接近于0）。因为现实中不仅存在推动它们相反变化的因素，也有推动它们朝着相同方向发展的因素。例如，考虑人口预期寿命的延长。在此前提下，纵然生育率保持不变导致每代新增人口数量相同，人均寿命的增加既会导致总人口规模的增加，也会推动人口老龄化的进程。［7］根据Takats模型，不难发现两个指标对住房价格的走势有相反的影响：更大的人口规模会推动住房价格，而更高的老年人口抚养比则会对住房价格形成下行压力。因此，只考虑其中一个指标会忽略人口结构变化的一方面影响。

总之，本文用perGDP来衡量经济发展对住房价格的影响，用总人口和老年人口抚养比来衡量人口结构变动对住房价格的影响。并且基于此模型，可以预期GDPPC和TPOP变量的系数为正，而OLDDEP变量的系数为负。

（三）扩展模型

本文在扩展模型提出以下假设：

假设1：新增住房量由政府控制，且政府符合理性人的假设。

假设2：对于行为人，新增住房和原有住房为同质产品。

根据假设1，政府的目标函数为：

其中，t1，t2分别为新增住房和原有住房销售额的固定税率，K˙t为t期新增住房供给，Kt为t期的住房存量。

住房需求函数为线性形式，即：

为简化分析，这里假设了住房存量的折旧为0。

由以上两式，可以得出政府税收最大化时的新增住房供给为：

这意味着，个人的最优储蓄不一定等于住房投资。本文假设存在一个银行系统，每期会提供储蓄与住房投资差额的贷款或存款服务，记为lt。则（7）改写为：

当个人的最优储蓄小于住房投资时，行为人会从银行借入资金购买住房，老年时期再归还本息；当最优储蓄大于住房投资时，行为人可以将这部分多余的资金存入银行，到老年时可以收回本息。

由上式t+1期和t期可以得到住房价格的演变路径为：

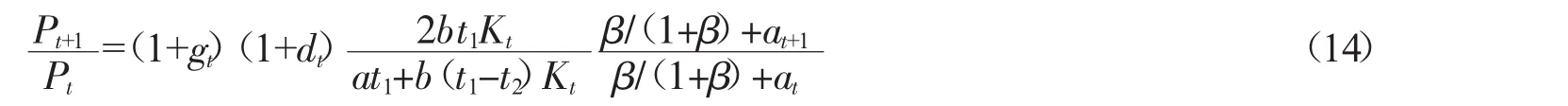
其中，at=lt/ytY，表示t期个人贷款或储蓄占个人收入的比例。

与Takats模型的结论一致，加入政府完全垄断供给市场的假设后，经济因素和人口因素对住房价格仍起着重要作用。［7］同时，住房存量、购房税率以及购房贷款比例都对住房价格有一定的影响。通过比较静态分析，在其他条件不变的情况下，本期住房存量越高，本期购房贷款比例越小，下一期购房贷款比例越大，则下一期住房价格相对于本期住房价格增长的越高。

三、实证模型和数据

（一）实证模型

住房是一个人一生中至关重要的消费品，而且一般情况下他或她会在年轻时买房而后终生消费，即一次购买终生消费。因此，从个体角度分析，消费者是否有购房需求与其年龄有很大关系，而站在整个社会的角度，相应年龄段的绝对人口和相对人口数量都对总的购房需求产生显著影响。这些分析可以看作Takats模型的直观解释。本文以Takats模型推导出的实证模型来进行回归分析：

这里Pit代表地区i在t时期的真实住房价格，perGDP为真实人均GDP，OLDDEP是定义的老年人口抚养比。最后，TPOP表示总人口。ε为随机误差项。［7］

（二）数据

在回归分析以及稳健性检验中，本文使用了中国和美国的地区面板数据。表1列出了所需数据及其来源。

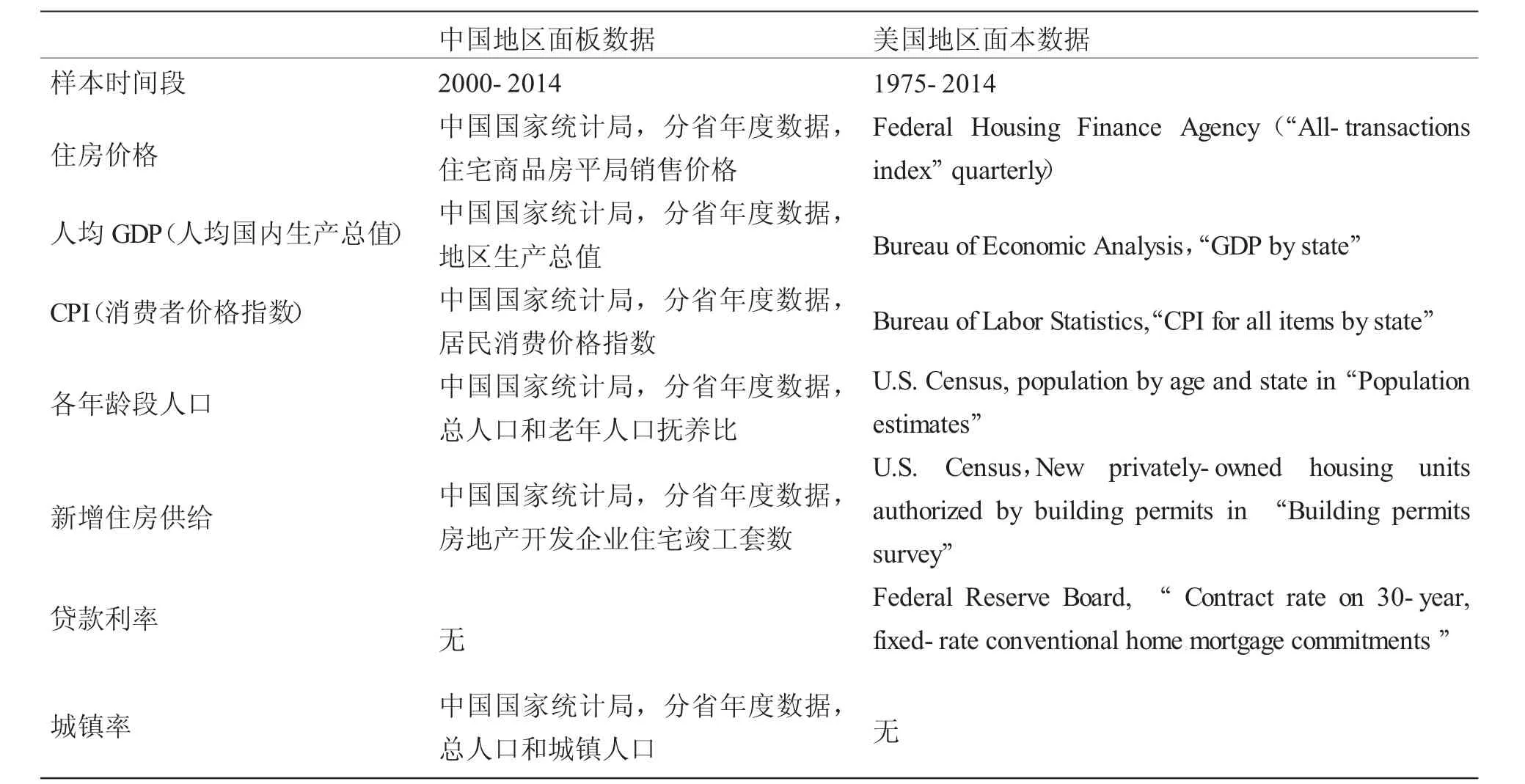
表1 所用数据的来源

（三）人口结构变动

图3和4分别展示中国、美国的老年人口抚养比及其增长率。与美国相比，目前中国的老年人口抚养比更低，但是增速正在加快。这意味着中国老龄化水平还有一定的上升空间。

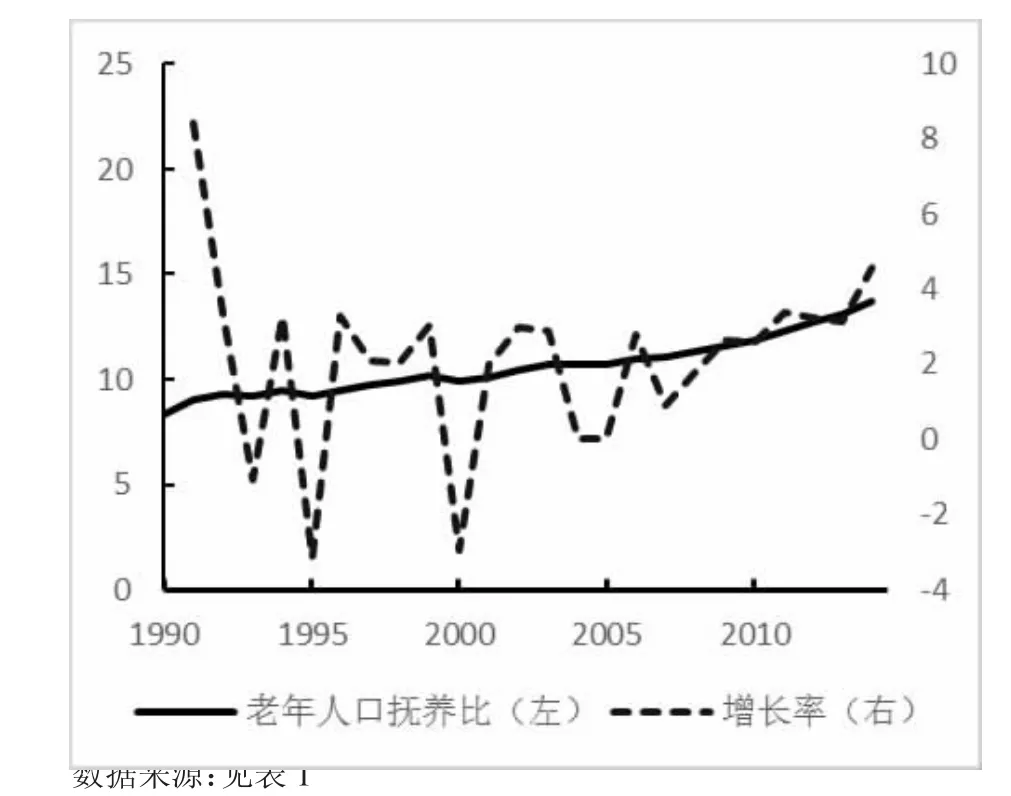
图3 中国老年人口抚养比及其增长率（％）

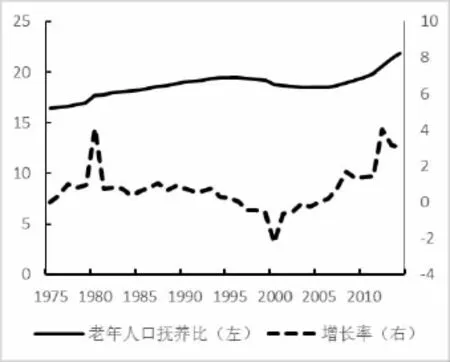
图4 美国老年人口抚养比及其增长率（％）

根据M-W模型估计，中国居民在20岁之后住房需求快速上升，30岁时达到20平方米/人的水平。［5］这也与大部分人在此年龄段开始购买住房的社会现象一致。为了更加清楚地看出适龄购房人群总量的变化，并结合实际社会生活情况，本文重点观察30～44岁年龄段人口数量。图5、6展示了两国30岁到44岁年龄段人口绝对数量的发展路径和预测。两国存在一个明显的区别是，中国该年龄段人口在2010年～2015年达到顶峰后不断下滑，在中度预测情况下，到2100年将回到20世纪50年代的水平。而美国该年龄段人口自20世纪90年代达到新的高度后一致保持平稳。产生这种差别的原因在于，在中国，该年龄段人口总数在“婴儿潮”之后随着人口出生数量降低而逐渐回落，而美国由于存在着大量的青年移民，可以保持着该年龄段人口的相对稳定。

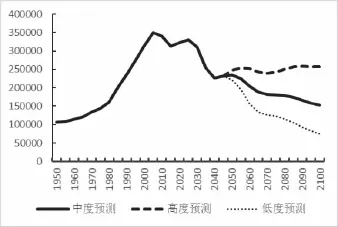
图5 中国30～44年龄段人口（千人）

图6 美国30～44年龄段人口（千人）

四、实证结果

（一）单位根检验

本文使用三种方法检验面板数据的稳定性：（1）Levin，Lin和Chu（简记LLC）所提出的检验方法。［8］（2）Harris和Tzavalis（简记HT）提出的检验方法。［9］并且这两种方法都假设面板单位存在共同单位根（common unit root）。但是，区别之处在于前者是基于n/t→0的检验，后者是基于T固定而n→∞的检验。（3）Im，Pesaran和Shin（简记IPS）提出的面板单位根检验假设面板数据中有n个相互独立的个体，即存在个别单位根（individual unit root test）。［10］

对于一个面板序列yit，假设其一阶AR过程由下式给出：

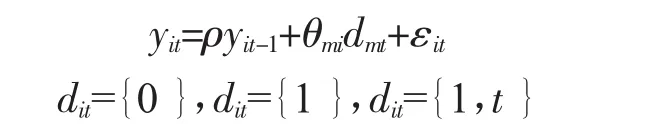
当i=1，2，…，N，t=1，2，…，T，m=1，2，3。当dit=1时，θmidmt表示个体固定效应，当dit={1，} t时，θmidmt表示个体固定效应和线性时间趋势。为了检验ρi=1，我们进行如下回归：

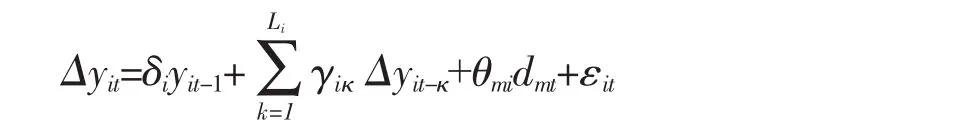
因为LLC检验和HT检验都假设存在共同单位根，因此它们的原假设和备择假设为：

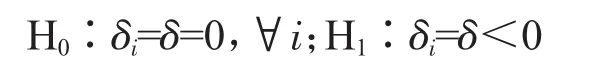
这里，δi=ρi-1。

而IPS检验假设地区之间存在着不同的单位根，因而其原假设和备择假设为：

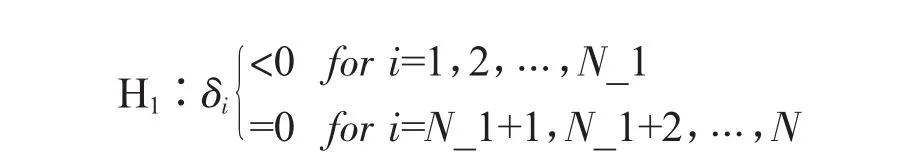
运用以上阐述的检验方法对真实住房价格，真实人均GDP，总人口，老年人口抚养比等变量的自然对数面板序列进行检验。结果如表2所示，对于全部变量，当取一阶差分形式时，都可以拒绝原假设，认为该时间序列平稳。

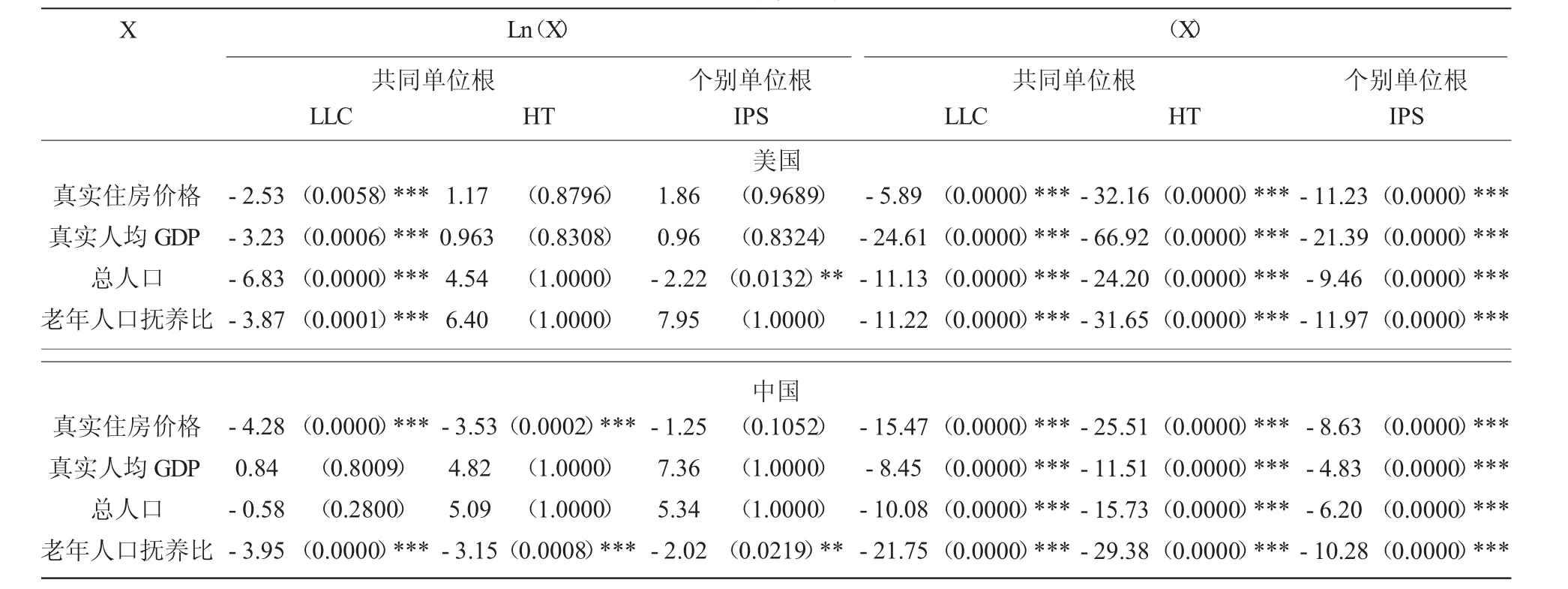
表2 单位根检验

（二）回归结果

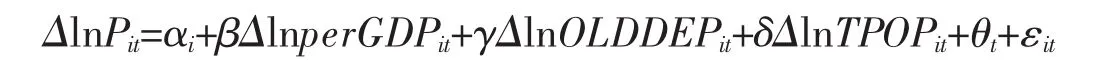
我们选择（15）的随机效应模型作为的基准模型（简称BM），即以下式进行回归分析：该式不同于（15）式的地方在于：①αi表示个体随机效应，②θt为时间固定效应，衡量了未被观察的全局共同因素，例如2008年美国次贷危机等。

回归结果展示在表3（时间虚拟变量的回归系数见附录1和附录2）。

首先分析美国地区面板数据的回归结果。三个解释变量都在1％的水平上显著，其系数的符号与前文理论模型的预期一致：人均GDP和总人口的系数为正，而老年人口抚养比的影响为负。这些系数的大小也有研究意义。它们可以被解释为弹性，因为本文采取了解释变量的一阶差分log形式。单独来看，当其他条件不变，住房价格相对于总人口的弹性接近于单位弹性，这意味着1％的总人口增长会带来大致1％的住房价格上涨；相反地，老年人口抚养比每增长1％，住房价格大致会下降4/5％。

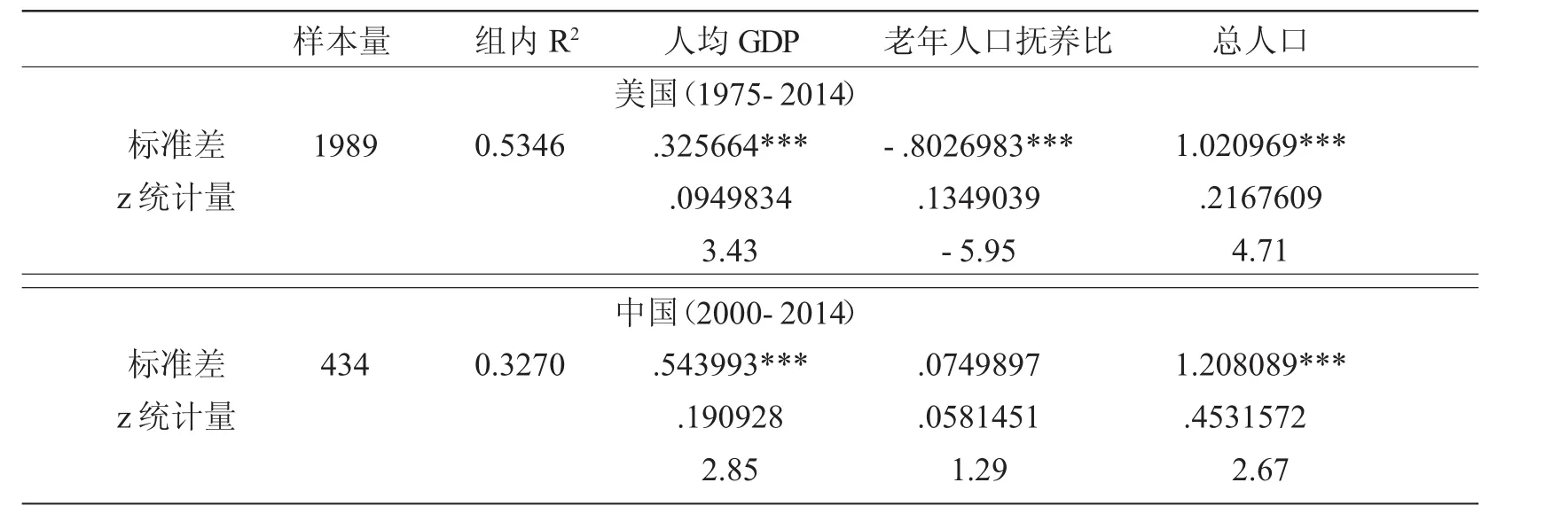
表3 带时间虚拟变量的基准模型的回归结果

相比美国，中国存在着更复杂的情况。首先，中国的人均GDP和总人口的影响都在1％的水平上统计显著，但是都比美国的该类系数高0.2。这表明，中国的住房价格对居民的收入和人口总数的弹性更大。其次，中国的老年人口抚养比的系数在统计上并不显著，并且在符号为正，这与预期的老年人口对房价的消极影响不一致。

对于这一现象，本文认为有如下解释：

（1）样本选择偏差。由于中国的商品住宅市场在1998年中国政府住宅分配市场化改革后才逐渐发展，目前可获得的中国省级住房价格数据只能追溯到2000年。在这一阶段，中国的人口老龄化问题已经开始显现，并且逐步严重，这与住房价格持续上升一直保持着一致。仅2000～2014这段时间的数据可能无法有效地衡量老年人口对住房价格的影响。

（2）模型设定偏差。Takats模型的隐含假设基于完全市场化的发达国家。［7］但是在中国，安居房制度和严格的户籍管理制度，甚至快速城镇化等因素都会导致由其得来的实证模型存在设定偏差。然而，在稳健性检验部分，本文加入城镇化率、新增住房等控制变量后，发现老年人口抚养比的系数仍为正。而安居房等制度是否对老年人口的购房意愿产生影响需要相关方面的深入分析，这超出了本文的研究范畴，在此不做论述。

（3）中国的特殊社会观念和现状。由于中国独特的家庭观念，中国的老年人“实际上”有很强的购房意愿，从而对住房价格有促进作用。徐建炜在进行OECD国家和中国的老年人口抚养比对房价影响时也有同样的发现。他指出，这一差异可能源于中国的市场化体制转型以及阶段性的人口政策有密切关系。［11］因为现在的老年人大多成长于计划经济时代，年轻时无须考虑货币购买住房，产生了大量的额外储蓄；中国自20世纪80年代以来的计划生育政策，造成了中国独特的“421”家庭结构，增强了上一代人对年轻人的“利他心理”。当住房商品化改革后，两代人的积蓄同时释放于住房市场，老年人有着强烈的动机帮助下一代购买住房。

同时，徐建炜也指出，当代老年人的来自转型之前的储蓄将在2015年左右释放完毕，其后将很难继续推高房价。随着老龄化的继续发展，老年人口抚养比的上升将逐渐对住房价格产生消极影响。［11］

（三）稳健性检验

回归结果在多种情况下都是稳健的（具体结果见表4）。首先，该结果对模型设定的改变是稳健的。当去掉基准模型的部分甚至全部人口结构指标后，在上节回归结果中显著的系数仍然显著，且符号相同（M1、M2和M3）。其次，本文的结果对模型的形式也是稳健的。M4为不带虚拟时间变量的随机效应模型，M5为固定效应模型，M6为带虚拟时间变量的固定效应模型。

表4 稳健性检验

（续上表）

再者，本文将新的变量加入基准模型中。对于美国，我们加入利率和新增住房供给，对于中国，我们加入城镇率和新增住房供给（回归结果见M7、M8和M9）。本文发现，对美国地区面板数据的回归中，利率的系数为负，这与理论的预期一致。中国数据的城镇化率的系数为正，这也符合经济学逻辑。但是对于新增住房供给，两国数据所得出的系数符号并不相同。中国的该系数为负，虽然绝对值很小但是统计上显著，这表明住房供给的增加会给住房价格带来下行压力。另一方面，美国的住房供给的系数为正且显著不等于零。这意味着在美国，存在由于住房价格的上升将导致住房供给增加的情况。

同时，基准模型的结果对不同的样本时间段的选择也是稳健的。以美国为例，我们将整个样本时期分为两段：1975年～1990年和1990年～2014年。通过各段的回归结果可以发现，与前一段的变量系数估计值相比，后一段的人均GDP和总人口两个变量的系数估计值相差不大。但是，其老年人口抚养比的系数估计值（-0.63）的绝对值明显小于前者（-1.08）。在1990年前，美国二战后婴儿潮一代步入成年，进入了住房市场，住房市场需求大增，此时的住房价格对老年人口的比例更加敏感。1990年之后，美国70年代生育低潮的一代进了住房市场，住房需求逐渐下降，因此，住房价格对老年人口的比例也缺乏弹性。

最后，本文将滞后一期的人均GDP变量加入基准模型中，用来消除潜在的内生性问题（M10）。结果同样表明基准模型的估计结果是稳健的。

五、结论

本文所分析的人口结构因素的波动很大程度上来源于一个现象——婴儿潮。在其初期，大量人口的出生，伴随着这一代人的成年，其所在的年龄段内人口绝对数量增加。同时，他们年轻时整个社会的老年人口抚养比不会大幅度上升。然而，随着婴儿潮一代渐渐老去，取而代之的是逐步的人口老龄化。

对于这一波动对住房市场的影响，本文研究发现：基于生命周期理论的代际交叠模型表明住房价格确实被人口结构因素影响，既包括总人口规模扩大的积极影响，也有人口老龄化带来的消极影响。本文也通过实证检验确认了这一影响的存在。但是，不同于美国，中国的老年人口似乎在过去十年里对本国的住房价格有着促进作用。这一特殊性极可能源于尚未成熟的住房市场。正如邹瑾提到，长期来看，中国的老年人的住房需求逐步得到满足，住房改革后两代人的积蓄同时发力于住房市场的特殊情况在未来将不会再现。［12］因而，本文认为在未来数十年，老年人口对中国的住房价格将不再具有推动作用。

综合以上分析，以及联合国对中国未来数十年的人口预测，本文认为在2030年之后，作为支撑中国近十年住房市场繁荣发展的动力之一，人口结构因素的影响将极有可能发生逆转。即使老年人口因为中国的特殊社会观念而带来的积极影响抵消了老年人口住房需求下降带来的消极影响，真正的购房适龄年龄段人口总量的明显下滑决定了人口因素不能再支撑住房价格的上涨。尽管这一反转不太可能直接导致住房市场崩溃，但是，其可能带来的住房市场的萎靡值得户主、房地产开发商以及政府的关注。

本文存在以下两方面的不足：一方面，理论模型的假设简单且外生变量过多，解释范围因此下降。采用代表性行为人生活三期的假设，即少年期、青年期、老年期，更能刻画真正的现实经济运行状况，并且可以据此考察少年人口抚养比是否对住房价格产生影响。同时，行为人在青年时买房作为储蓄手段并在老年时将房子卖出以消费的假设也过于简化，现实生活中的居民的行为肯定更加复杂。另一方面，实证分析中住房价格的数据的选取也存在问题。为了研究方便，本文均采用了新建住宅的价格作为该地区的房价代表，未能考虑二手房市场以及自建房屋的情况。而这些因素可能会对结果产生一定的影响。同时，Takats模型中的经济活动人口可能与现实生活中的总人口和老年人口抚养比例不存在稳定的关系。考虑到少年人口（20岁以前）以及一定的失业率，这些因素都会导致用总人口和老年人口抚养比来估计回归模型有一定的偏差。

［1］杨华磊,温兴春,何凌云.中国婴儿潮下的城镇住房需求［J］.中国经济问题,2015（2）:49-60.

［2］MANKIW N Gregory,David N.Weil.Baby Boom,Baby Bust and the Housing Markets［J］.Regional Science and Urban Economics,1989,19（2）:235-258.

［3］HAMILTON B W.The Baby-boom,the Baby Bust,and the Housing Market:a Second Look［J］.Regional Science and Urban Economics,1991（21）:547-552.

［4］GREEN,HENDERSHOTT.Age,Housing Demand and Real House Prices［J］.Regional Science and Urban Economics,1996（26）:465-480.

［5］陈斌开,徐帆,谭力.人口结构转变与中国住房需求:1999～2025——基于人口普查数据的微观实证研究［J］.金融研究, 2012（1）:129-140.

［6］陈彦斌,陈小亮.人口老龄化对中国城镇住房需求的影响［J］.经济理论与经济管理,2013（5）:45-58.

［7］TAKATSElod.Agingand House Prices［J］.Journal ofHousingEconomics,2012（21）:131-141.

［8］LEVINCF,CHUCS.Unit Root Tests in Panel Data:Asymptotic and Finite-sample Properties［J］.Journal ofEconometrics,2002（108）:1-24.

［9］HARRIS R D,TZAVALIS E.Inference for Unit Roots in Dynamic Panels Where the Time Dimension is Fixed［J］.Journal of Econometrics,1999（91）:201-226.

［10］IMKS,PESARAN MH,SHIN Y.Testing for Unit Roots in Heterogeneous Panels［J］.Journal of Econometrics,2003（115）: 53-74.

［11］徐建炜,徐奇渊,何帆.房价上涨背后的人口结构因素——国际经验与中国证据［J］.世界经济,2012（1）:24-42.

［12］邹瑾,于焘华,王大波.人口老龄化与房价的区域差异研究——基于面板协整模型实证研究［J］.金融研究,2015（11）: 64-79.

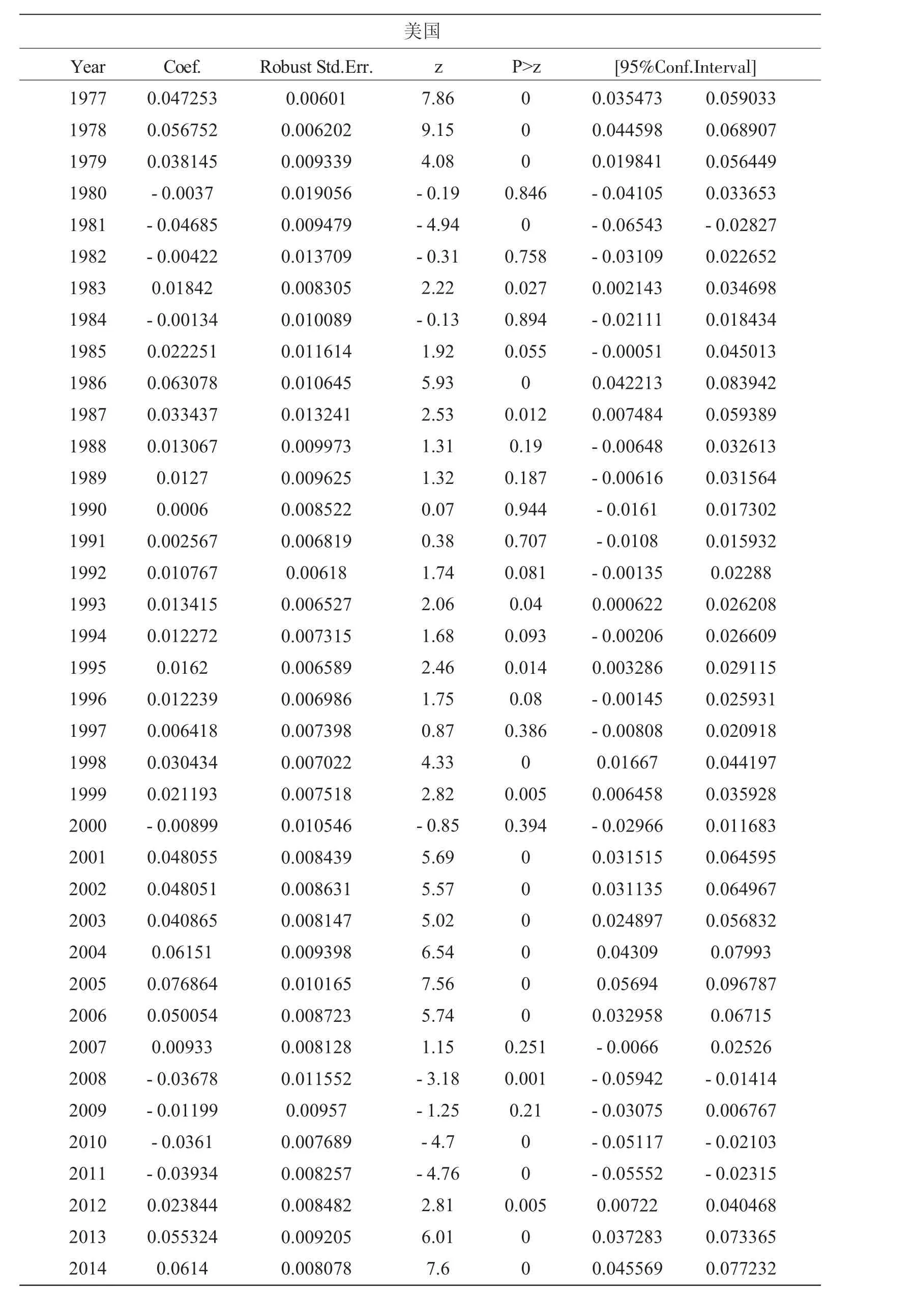
附录1基准模型回归的时间虚拟变量系数的估计结果（美国）

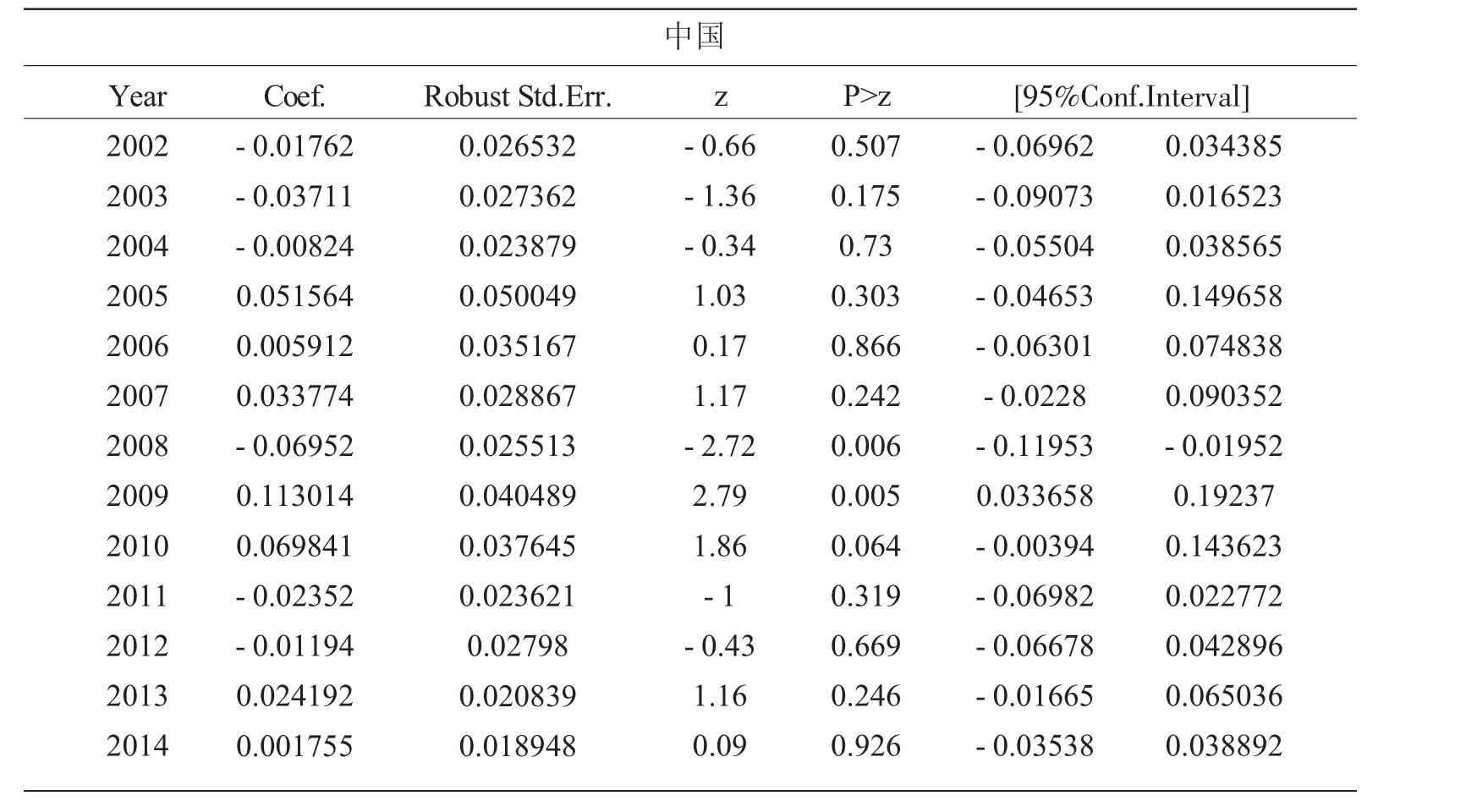
附录2基准模型回归的时间虚拟变量系数的估计结果（中国）

（责任编辑：张惠fszhang99@163.com）

The Effect of Baby Boom on House Price: Insight into the Demographic Changes

WANGPu

（Department ofMathematics,HongKongUniversityofScience and Technology,Hongkong999077,China）

This paper has studied the influence of Baby Boom on house price,which is captured by the effects of the demographic changes.The baby boom generation into its house-buying years would lead to the increase in housing demand,which is expected to a higher house price.Not only theoretically but also empirically this paper shows the impact of demographic changes started form baby boom in house market.A small overlapping generation model set up with lifecycle implies that demography,as well as economic factors,is a house price driver.In the empirical model using a regional panel data in USA and China,the demographic factors are represented by the total population（TPOP）and the old dependency ratio（OLDDEP）,which are expected to have positive and negative influence in house price separately.The regression results show that,in USA,real estate prices in a region are inversely correlated with OLDDEP,and positive correlated with TPOP.In China, however,the old people have a positive impact probably due to her special national conditions or too short sample period（2000-2014）.But,as many other Chinese scholars have mentioned,the impact of OLDDEP would turn round with the development of house market gradually.The robustness of the regression results also is checked in this paper.

baby boom;demographic factor;old dependency ratio;house price;random effect model

F293.35

A

1008-018X（2017）01-0076-12

2016-12-12

王璞（1993-），男，山西运城人，香港科技大学数学系2016级硕士研究生。