基于云电送粤的小扰动稳定性研究
2017-03-08钏助仁
钏助仁
摘 要:采用多机电力系统的特征值分析方法,应用电力系统计算分析综合程序对云电送粤交直流混联输电的小干扰稳定进行了分析研究,给出了电网弱阻尼的振荡模式,并为下一步整定电力系统稳定器参数提出指导性建议。
关键词:小扰动稳定 电力系统稳定器(PSS) 振荡模式
1.引言
在电力系统中,发电机并联运行时,在扰动下会发生发电机转子间的相对摇摆,同时在缺乏阻尼时引起振荡持续,称电力系统低频振荡。此时输电线路上的功率也随之发生相应的振荡,频率很低(一般为0.2~2.5Hz)。低频振荡常出现在重负荷、长距离的输电线路上,云南的电网在建设过程中曾经发生过局部区域的低频振荡,不过随着网架结构的增强,一些振荡问题已经逐步消除。但由于快速、高增益倍数励磁系统的广泛应用,它对电力系统的负阻尼效应使电网的低频振荡又显露出来。本文对云电送粤系统下的小干扰动态特性进行了研究,并对系统的运行给出了建议。
2.理论基础
电力系统在运行中总是不能避免小干扰,所以,对电力系统的小干扰进行稳定性分析,就能判断电力系统在给定的运行方式下能否稳定,是电力系统分析中最基本和最重要的任务之一。可借助李雅普诺夫的线性化方法对电力系统小干扰进行稳定性分析。此方法主要针对系统的线性化状态空间方程式的特征根和特征向量来分析,将系统动态行为的非线性微分方程在运行点附近线性化,计算线性化系统状态矩阵的特征值、左右特征向量以及阻尼比、机电回路相关比的灵敏度等,从而分析判断系统在小干扰下的行为特征、参与因子和特征值对应的参数。
按上述方法系统的动态特性一般由一组非线性微分方程组与一组非线性代数方程组来描述: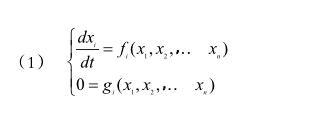
各变量可表示为其初始值与微增量之和(在平衡点 附近线性化):

状态方程表述的线性系统的小干扰稳定性由状态矩阵的所有特征值来决定。引入Lyapooov的第一稳定性定理,可知:如(6)式的所有特征根都有负实部,则原系统的平衡状态是渐近稳定的;如(6)式的特征根至少有一个具有正实部,则原系统的平衡状态是不稳定的;如(6)式的特征根有实部为零的情况(称临界情况),则原非线性系统(1)的稳定性不能从线性化方程(6)来判断,此时須考虑原方程展开式中二次或更高次项的影响。对实际运行的系统来说,分析临界下的情况没有什么意义,可把它看作小干扰稳定的极限情况。所以,分析系统在某运行点的小干扰稳定性问题,可归结为来求解状态矩阵A的所有特征值的问题。因此,电力系统小干扰稳定性分析的一般过程可归结为:先形成状态矩阵A,再根据它的特征值的性质来判断系统是否稳定。本文主要关注电力系统的机电振荡模态。
3.研究方法
针对电力系统小干扰稳定性问题的研究,可采用时域分析法或频域分析法。
频域分析法主要是指特征值分析法(经典控制理论中的稳定判据及D域法等方法,在复杂多机系统中应用存在困难)。一个多机电力系统可以用方程式:

从以上分析可看出,用频域分析法来研究电力系统小干扰的稳定性,其最大的优势是可以纵览全局。在研究计算结果时,可得到一个N机电力系统所有机电振荡模式的阻尼特性信息(主要看是否存在负阻尼、零阻尼或弱阻尼振荡模式),同时还能知道这些模式的振荡频率、衰减系数和阻尼比。如再进一步采用特征向量分析、参与矩阵分析或特征根灵敏度分析来进行研究,还可得出产生负阻尼的原因和地点。
频域法的主要缺点是,它采用了线性化的电力系统数学模型,不能很好地考虑各种非线性因素。
另外时域分析法用来分析电力系统小干扰的稳定性,其主要优点是结果清晰、明了、直观,同时还可考虑更多的机组,且所有机组可用更高阶数的方程来描述,这样可得到更加准确的模型,同时还可以更加详细地考虑负荷的动特性与静特性,从而使研究结果更接近实际。

4.云电送粤系统的小干扰稳定性计算分析
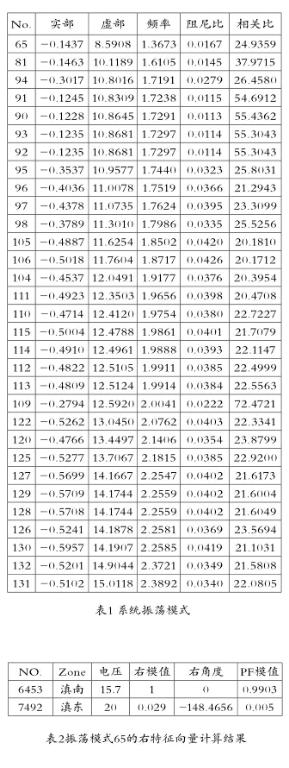
云电送粤输电系统中,以楚雄换流站的HVDC控制系统中,整流侧采用定电流控制方式,逆变侧采用定电压控制方式,当调节增益为K=0.01,时,系统振荡模式如表1所示。
从表1可以看出:振荡模式82、99和100是负阻尼,根据前文划分要求属于极弱阻尼范围。对0~4%弱阻尼范围对振荡模式进行分析: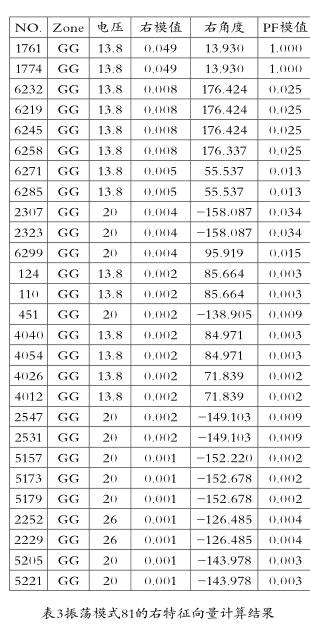
从表2的参与因子上看,模式65仅有滇南的0.9903和滇东的0.0050。其中滇南机组的右模值较大,而滇东机组的右模值较小,反映了振荡模式65是滇南机组比滇东机组的振荡强,两者的相位相差-148.4656°,表明滇南机组相对于滇东机组振荡。振荡模式65右特征向量模态图如图1所示:
从表3的参与因子上看,模式81都在地区GG内,其中以1761和1774的参与因子最大,并且有特征值模也是最大,表明这是区域内的振荡。这两组与2307、2323、2547、2531、5157、5173、5179的相位相差加大,接近180°,表明1761和1774相对于其他机组振荡。而除了1761和1774这两组以外,的机组相位相位相差不大,它们基本上是同步协调。振荡模式81右特征向量模态图如图2所示:

从表4的参与因子上看,模式91都在地区GG内,属于同一母线内的不同机组,参与因子都为1,相位相反,是厂内的两机组的相互振荡,并且模都为1,是两机组的强相互振荡。振荡模式91右特征向量模态图如图3所示:
从表5的参与因子上看,模式109都在地区GX内,参与因子与模排在第1~6位的是323、313、315、317、319、321机群,与排在第7~10位的相位相反,两者相差180°左右,属于单机群对区域内的其他机群的相互振荡。从母线名來看,同一母线名下的基本上是同步协调的,由于特征值的模整体来看都不大,振荡比较弱。振荡模式109右特征向量模态图如图4所示:
5.结论
因云南电网网架结构比较牢固,经以上计算可得出,区域电网之间没有弱阻尼的低频振荡。只有在电网内部有极个别的机组之间才有弱阻尼的低频振荡。同时根据以上表1至表5提供的振荡模式与对应机组的特征向量,对参与因子参数比较大的特征向量所对应的机组有针对性地整定它的发电机组电力系统稳定器的参数,就可以有效的抑制系统低频振荡的产生。
参考文献:
[1]谷寒雨.大型电力系统小信号稳定特征值分析方法研究[D].上海:上海交通大学,1999.
[2]Kundur P.Power System Stability and Control[M].New York: McGraw-Hill,1994.
[3]励刚,苏寅生,陈陈.面向对象的多谱变换隐式重启动Arnoldi算法[J].电力系统自动化.2001,25(4):24-27.
[4]谷寒雨,陈陈.一种新的大型电力系统低频机电模式计算方法[J].中国电机工程学报.2000,20(9):50-54.
[5]励刚.小干扰稳定性分析及面向对象软件包的开发研究[D].上海:上海交通大学,2000.
[6]刘晓鹏,吕世荣,郭强等.多重Caylay变换用于电力系统小干扰稳定性的部分特征值分析[J].电力系统及其自动化学报,1998,10(6):1-7.
