有痕设计 无痕育人
2017-03-07孙琪斌
【编者按】2016年11月,江苏省第28届“教海探航”征文颁奖仪式暨全国名师课堂教学观摩研讨活动在江苏省南通市通州区举行。此次活动中,省内外多位名师的展示课和讲座受到与会教师的好评。为进一步发挥名师的引领作用,我们约请了本次活动中授课教师撰写了相关文章,在“特别策划”栏目中分四期连载刊发,本期呈现的是数学学科的内容。
【摘 要】数学学科育人的核心价值主要体现于数学的理性精神以及蕴含其中的数学思想方法。从某种意义上说,数学学科育人的过程镶嵌于“发现问题、提出问题、分析问题、解决问题”的过程之中。对学生而言,在学习数学时养成的基于理性思考、严谨求证的问题解决习惯将会让他们受益终生。本文主要以运用圆的基本性质探究画垂线的新方法为例,介绍了开展数学学科育人的部分做法。
【关键词】圆的基本性质;数学问题解决;数学学科育人
【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009(2017)11-0025-04
【作者简介】孙琪斌,上海市嘉定区教研室(上海嘉定,201808)教研员,高级教师,山东省特级教师,上海市特级教师。
“问题是数学的心脏”[1],也是数学学科育人的基本载体。基于这样的思考,我们认为:(1)数学学科育人必须立足数学教材、立足数学问题、立足数学课堂、立足典型课例、立足对话交流;(2)数学学科育人的核心价值主要体现于数学的理性精神、数学的思想方法以及从数学的角度解决问题的思维方式;(3)数学学科育人的过程镶嵌于“发现问题、提出问题、分析问题、解决问题”的过程之中。
下面以运用圆的基本性质探究“经过一点画已知直线的垂线”的方法为例,谈谈我们在开展数学学科育人方面的部分思考。
一、归纳提炼,提高抽象能力
本节课我们探讨的是利用圆的性质“经过一点画已知直线的垂线”。因此,首先要解决的就是对“圆的性质”的知识的回顾。在课前的学情调研中,我们发现学生能够比较容易地说出平行线的性质、全等三角形的性质、平行四边形的性质、相似三角形的性质;也能够轻松地说出垂径定理等教学内容,但是当我们问到“圆有哪些性质?”的时候,许多学生都是一脸茫然。为此,我们设计了一个课堂活动:用一句话归纳概述圆的性质。先由学生自主思考,然后小组合作向全班展示。
教师在学生活动的基础上做出分析和归纳。1872年,德国数学家克莱因(Klein)在“爱尔兰根计划书”中提出:每一种几何学都联系一种变换群,每种几何学所研究的内容就是在这些变换群下的不变性质。从这个意义上说,圆的有关性质,其实就是关于圆的对称性的性质。事实上,垂径定理刻画的是圆的轴对称性;同圆或等圆中的四组量(两条弧、两个圆心角、两条弦、两条弦的弦心距)之间的关系,所刻画的是圆的旋转不变性。由此,我们可以将圆的基本性质抽象、提炼为一句话:圆的基本性质,就是与圆的轴对称、旋转对称(含中心对称)有关的性质。具体内容如图1所示。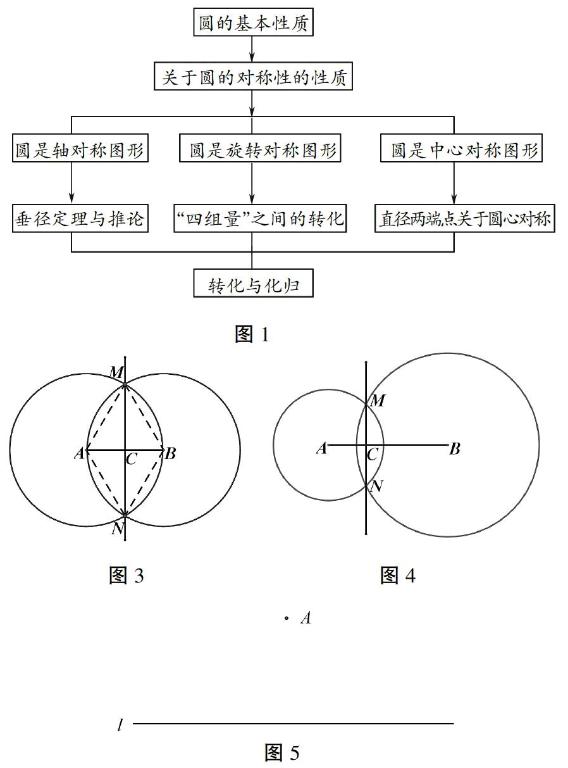
(设计说明:从回顾整理圆的有关性质,到用一句话、一张图进行归纳概述,数学的抽象已经蕴含其中。事实上,抽象概括能力、逻辑推理能力、基于数据的分析挖掘的实证能力,在人的一生的各个发展阶段,都发挥着重要的作用。本课,我们结合圆的基本性质的梳理回顾、提炼归纳,旨在运用数学抽象的基本思想历练学生的抽象概括以及交流表达能力。)
二、发现探究,提高解决问题的能力
1.温故知新,在回顾线段垂直平分线的画法的过程中发现问题、提出问题。
教师可以提出如下问题串:
(1)学了圆的这些性质,有用吗?(调研过程中,我们发现学生普遍认为学习圆的这些性质没有用。)
(2)如图2,还记得画线段AB的垂直平分线的方法吗?(尺规作图)
在画图过程中有这么一句话:“分别以点A、B为圆心,大于AB长为半径画弧”,其中的半径为什么要“大于AB”?你能运用圆的有关知识解释这个现象吗?你能说出作图方法背后的原理吗?(操作几何画板,呈现两圆相交、外切、相离的情景)
(3)在画线段AB的垂直平分线的过程中,我们以点A、点B为圆心,以大于AB长为半径画弧。假如我们以线段AB的长为半径画圆(如图3),会出现什么图形呢?你可以运用圆的有关性质解释作图方法背后的原理吗?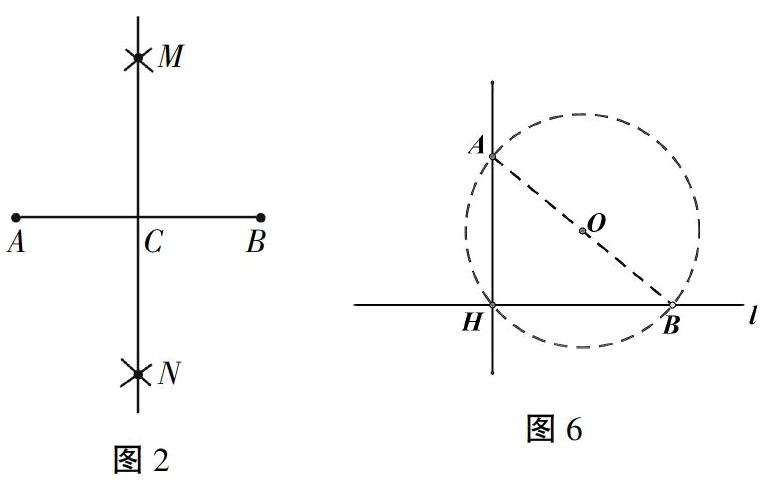
(4)在画线段AB的垂直平分线时,我们以点A、点B为圆心画弧所使用的半径是相等的。如果使用的半径不相等,那么直线MN与AB之间又有怎样的关系呢?(如图4)你能证明你发现的结论吗?
(5)如图5,已知直线l与直线l外的一点A,依据圆的基本性质,过点A作直线l的垂线,你们还可以设计出新的画图方法吗?(以小组为单位设计)
(设计说明:在上述问题串中,问题(5)才是我们最终想要探讨的问题,但前面的问题就像是一个个台阶,帮助学生从熟悉的旧知识中发现问题,并指向用圆的性质来做出解釋。这种温故而知新的设计极大地调动了学生的积极性。)
2.且学且用,运用圆的性质探究画垂线的新方法。
结合上面的问题(5)开展教学活动,学生以小组为单位进行展示汇报。具体方法如下。
方法1:如图6,在直线l上任取一点B,连接AB。以AB为直径作☉O,交直线l于点H。则直线AH即为所求。(依据:直径所对的圆周角是直角。)
方法2:如图7,①在直线上任取一点B,以点B为圆心,BA为半径画☉B,交直线于点C;②以点C为圆心,CA为半径画☉C,将☉B与☉C的另外一个交点记为D,则直线AD即为所求。(依据:平分弧的直径垂直平分弦。)
方法3:如图8,在直线l上任取两点B、C(B、C两点不重合),以点A为圆心,以AB半径画圆交直线l于点D;以点A为圆心,以AC半径画圆交直线l于点E。AE、AC分别交以AB半径的圆A于F、G,连接EF、CG,EF与CG相交于点P,直线AP即为所求。(依据:可证点A、P均在线段EC的垂直平分线上。)
方法4:如图9,任取一点B,使点B与点A位于直线l的两侧,以A为圆心、AB为半径画圆,交直线l于点C、D;作圆心角∠CAD的平分线AE,则直线AE即为所求。(依据:可证△ACH≌△ADH。)
方法5:如图10,以点A为圆心画圆,☉A与直线交于点C、D,取CD的中点E(本质是作线段CD的垂直平分线),则直线AE即为所求。[依据:平分弦(不是直径)的直径垂直于这条弦,且平分这条弦所对的弧。]
南通市通州区育才中学九年级七班的学生先后发现了上面的几种方法。除了教材中的画法外,在笔者多次的教学中,还有其他班的学生发现了如下画法。
方法6:如图11,在直线l上任取一点B,以B为圆心,BA为半径画圆B,交直线l与C、D,利用直径所对的圆周角是直角,易得∠CAD=90°;以A为顶点,以AD为一边作∠DAE=∠DCA,交线段CD于H,则直线AE即为所求。
方法7:2013年11月,在杭州市建兰中学的课堂上,九年级学生何佳祺在下课前给出的画法见图12。(其中,借助了几何画板的直观演示与师生互动,该课教学视频已经被浙江出版联合集团、浙江电子音像出版社出版。)
取异于点A的点B,以AB为直径作圆c1,交直线l于点D,AB与l的交点记为E。以A为圆心,DB为半径作圆c2,交射线AD于点F。以A为圆心,DE为半径作圆c3。以F为圆心,EB为半径作圆c4,圆c4交圆c3于点G,则直线AG即为所求。
三、在有痕设计中无痕育人
2016年11月,在南通市通州区育才中学九年级七班上课时的教学小结环节,我再次带着学生回到教学目标,回到圆的基本性质,再次询问学生:同学们再来想一想,学习圆的这些性质,有用吗?
许多学生不约而同地回答:有用。
事实上,学生走上社会之后将会遇到许许多多的问题。这些在学校学习数学时养成的基于理性思考、严谨求证的问题解决习惯将会伴随他们一生。本节课,我们并没有带领学生做大量的习题,而是引导学生回顾圆的基本性质,回顾熟悉的基本作图(基本作图的背后都用到了圆的性质),在回顾线段垂直平分线、角平分线的画图过程中发现问题、提出问题、分析问题、解决问题。在解决问题的过程中,学生身处其中所经历的困惑、领悟,则是数学学科育人的关键。
当学生带着激动的心情汇报展示其刚刚发现的研究成果时,当他们在教师以及学习同伴的眼里看到自己的成就时,那么对数学的兴趣将在顷刻之间油然而生。喜欢数学课、爱做数学题、对数学感兴趣、在应用数学的过程中理解数学、享受数学。我们的数学教学若能够如此,那么学科育人已在其中。
关于数学学科育人,需要注意两个问题:其一,学科育人不能形式化,贴标签式的学科育人,效果甚微;其二,学科育人不能泛化,不能一提到学科育人,就是教学设计的每个细节,课堂上的分分秒秒都是学科育人。数学学科育人,最关键的就是育人无痕,润物无声。
我们来做一个选择题,以判断自己是否已经具备了无痕育人的潜质:阅读下面的三个语句,并从中选择一个语句用在教案上。
(A)语句1;(B)语句2;(C)语句3;(D)玩文字游戏,没有多少意思。
语句1:梳理圆的有关性质,在温故知新的过程中渗透问题意识;在用一句话、一张图概述圆的有关性质的过程中,渗透数学抽象;在经过一点画已知直线的垂线的过程中渗透转化与化归等思想方法。
语句2:梳理圆的有关性质,在温故知新的过程中体会问题解决;在用一句话、一张图概述圆的有关性质的过程中,体会数学抽象;在经过一点画已知直线的垂线的过程中体会转化与化归等思想方法。
语句3:从发现问题、提出问题、分析问题、解决问题的视角梳理圆的有关性质,温故知新;运用数学抽象的思想方法尝试使用一句话、一张图概述圆的有关性质。运用转化与化归的思想方法研究过一点画已知直线的垂线的方法。
假如您选择了A或D,那么对于您而言,离数学学科的无痕育人可能还有距离。
为什么这样说呢?我们且从其中的行为动词“渗透”谈起。《现代汉语词典》中对“渗透”一词的解释是:比喻一种事物或势力逐渐进入到其他方面(多用于抽象事物)。但是,数学思想方法是数学本身固有的,而且是数学课程的核心。对于数学学科本身固有的思想方法,我们还需要“渗透”吗?数学思想方法已经如同血液浸润于数学的任何地方。事实上,描述数学思想方法的行为动词有很多,如“体会”“感受”“领悟”“经历”“体验”等等。
若仅仅只是使用类似“渗透”这个行为动词表述与数学思想方法相关的目标,问题也不是很大,但是当我们习惯于运用“贴标签”的方式进行数学思想方法教学,习惯于开展“口号式”的数学学科育人,那么真正的问题就出现了。
其实,我们期望的选项是C。为什么这样说呢?当数学思想方法真正融入数学教师的灵魂深处的时候,当数学思想方法能够自然而然地呈現于数学教师的言谈举止之中的时候,当我们能够自觉、主动地从数学抽象的视角设计“用一句话、一张图概述圆的有关性质”教学活动的时候,当我们自觉运用转化与化归的思想方法将经过一点画已知直线的垂线与画线段的垂直平分线以及画角的平分线等内容联系在一起的时候,当我们能够主动运用发现问题、提出问题、分析问题、解决问题的理念设计“圆的复习”教学活动的时候,我们的数学教学可能就走进了知行合一的境界,我们的学科育人可能就走进了无痕育人、润物无声的境界。有些数学教师之所以喜欢在教学小结的时候,用“贴标签”的方式告诉学生“这节课我们还使用了类比的思想方法”,主要还是因为其潜意识内的数学思想方法游离于数学教学内容之外的缘故。
读到这里,有些教师也许会说,无痕育人,真的无痕吗?我们在备课时所设计的教学活动,如本课從画线段的垂直平分线引出经过一点画已知直线的垂线的活动,这属于有痕设计还是无痕设计呢?学生又怎么可能想到从画线段的垂直平分线的过程中发现问题、提出问题呢?
我认为,开展数学学科育人,我们的教学设计的确是有痕的;我们选择资源、使用资源的角度与方法,也是有痕的;我们在课堂上进行的教学活动也是有痕的;但是我们期望的教学效果是无痕的。我们期望的境界是学生在经历用一句话、一张图概述圆的有关性质的教学活动的过程中,数学的抽象可以浸润到他们的灵魂深处;我们期望能够引导学生在参与“分别以点A、B为圆心,大于AB长为半径画弧”的数学活动的过程中,能够从两圆相交、外切、相离等位置关系的角度体会“大于AB”这个规定的道理。我们期望能够借助从画线段垂直平分线的过程中两次画弧所使用的半径相同的问题引出“假如两次画弧所使用的半径不相等呢?所画出的直线还是线段的垂直平分线吗?”等问题,自然而然地引导学生经历发现问题、提出问题、分析问题、解决问题的过程。当他们走入社会后,在生活中、在学术上遇到了问题,我们期望,我们这些数学课堂上的数学问题解决的经历,以及内化于心的数学问题解决意识,能够帮助他们解决生活上的问题、学术上的问题。
有痕设计、无痕育人,我们所期待的数学学科育人,大致如此。
注:本节课的原始素材(利用圆的性质画已知直线的垂线的问题)最初由安徽省马鞍山市成功学校数学组的高道才、范宏业老师提供(2013.09)。本节课先后在杭州市建兰中学(2013.11)、上海市民办华二初级中学(2013.12)、南通市通州育才中学(2016.11)、北京市第十八中学(2016.12)等学校与九年级的学生进行过交流。对于上述学校的师生,一并致谢。
【参考文献】
[1]HALMOS P. R.,弥静.数学的心脏[J].数学通报,1982(02).
[2]教育部.义务教育数学课程标准(2011年版).[M].北京:北京师范大学出版社,2012.
[3]米山国藏.数学的精神、思想和方法[M].毛正中,吴素华,译.成都:四川教育出版社,1986.
[4]怀特海.教育的目的[M].徐汝舟,译.北京:生活·读书·新知三联书店,2002.
