基于ARMAGARCH模型的资金流预测方法

周海峰

摘要摘要：金融服务机构的资金流动具有非线性、周期特性和不稳定性等特点，对资金流的准确预测有助于提高资金利用率和抵御金融风险的能力。通过分析资金流的特点，使用差分方法将资金流转化成增益序列，在增益序列上构建ARMAGARCH模型进行分析，并设计了一种确定模型参数的方法。结果显示，与简单ARMAGARCH模型、GMAR模型和GMSARIMA模型相比，该方法具有最小平均绝对误差（MAE）和平均绝对百分比误差（MAPE），同时精确预测的点数也最多，因此能够较好地对资金流入流出情况进行预测。

关键词关键词：资金流预测；ARMAGARCH；GMAR；GMSARIMA

DOIDOI：10.11907/rjdk.161744

中图分类号：TP319文献标识码：A文章编号文章编号：16727800（2017）001010404

引言

随着互联网金融的发展，采用精确的方法对银行等金融服务企业的日常资金流动情况进行预测，有利于管控风险，提高企业经营利润。对于如蚂蚁金服、P2P金融等金融融资平台，如何既保证资金流动性风险最小，又满足日常业务运转成为亟待解决的问题，精准地预测资金的流入流出变得尤为重要。

由于资金流量大，具有宏观效应，因而可对其建立时间序列模型进行分析。目前流行的时间序列模型有自回归（AR）模型、自回归移动平均（ARMA）模型、差分自回归移动平均（ARIMA）模型、ARIMA季节性（SARIMA）模型等。如齐立新等[1]利用AR模型对海洋环境噪声信号的时间序列进行仿真分析，取得了较高的预测精度；谭巧巧等[2]利用AR模型对WSN中的流量进行预测，从而减少了数据传输次数，并降低了能量消耗；王志坚等[3]对我国社会消费品零售总额年度数据进行ARMA建模，并用该模型预测未来三年社会消费品零售总额，发现预测值与实际值相对误差很小，模型拟合效果良好；许凤华等[4]利用ARMA模型对小麦价格指数进行预测，预测精度较好；崔振辉等[5]利用ARIMA模型对店里的视频业务流量进行分析和预测，提高了流量预测拟合精度；陈夫凯等[6]利用ARIMA对我国城镇化水平的短期数据进行预测，取得了较好的预测效果；Kumar S V等[7]使用ARIMA季节性模型对短期交通流进行预测，数据经过平滑处理后，使用ACF和PACF选择出合适的ARIMA季节性模型，并进行预测分析，通过平均绝对误差百分比（MAPE）对结果进行评判；Valipour M[8]使用ARIMA季节性模型和ARIMA模型对美国径流进行长期预测，结果发现ARIMA季节性模型有更好的预测精度。

但是这些预测模型的预测精度还有待提高，提高预测精度的一种常用方法是与灰度（GM）模型进行混合预测，常见模型有GMAR模型和GMARIMA模型（或ARIMA-GM模型）。如王翠翠等[9]利用GM（1，1）-AR模型和AR模型对地耕层土壤水分进行预测，预测平均相对误差为3.18%和7.3%；高宁等[10]建立GMAR模型预测高层建筑物沉降变形，分别对趋势项和随机项进行预测，取得了较好的预测结果；李程等[11]提出基于ARIMA-GM的组合预测模型，并对民航货邮周转量进行了较准确的短期预测，结果显示组合模型能提高预测精度；罗洪奔[12]提出了一种基于灰色-ARIMA的金融时间序列智能混合预测模型，首先建立金融时间序列灰色预测模型，用ARIMA的残差预测结果对灰色预测模型进行补偿，该模型较单纯的灰色预测算法和神经网络算法有更高的准确率。

由于广义自回归条件异方差模型（GARCH）在处理数据异变性方面具有很大优势，因而在混合预测模型中也常被采用。其中比较经典的模型有ARMAGARCH模型，其分别对均值和方差建模，适用于估计或预测金融时间序列数据的波动性和相关性。如陈彦辉[13]运用ARMAGARCH模型对恒指的隐含波动率指数进行预测，结果显示ARMAGARCH模型比ARMA模型更适合对恒指隐含波动率进行建模；李晶等[14]考虑到干散货运价指数的日收益率服从ARCH过程，建立了ARIMA-GARCH模型对BDI进行波动性研究，结果表明，该模型能很好地反应干货价格指数波动规律及敏感性；闫冬[15]建立ARMAGARCH预测模型，以2007年10月08日～2011年11月4日997个上证指数收盘价格为样本，对综合预测模型进行估计，并用随后五天的上证指数收盘价对综合预测模型进行检验，检验结果表明模型有效地刻画了上证指数的短期变化；王洪瑞等[16]在ARMA模型基础上，建立了GARCH模型对残差的方差进行了修正，最后以宜昌水文站1949～2001年日径流数据为例进行应用验证。

考虑到资金流具有不稳定的特性，本文通过差分处理首先将资金流转换成增益序列，然后利用ARMAGARCH模型对增益序列进行建模，并在蚂蚁金服提供的用户交易数据上进行资金流预测，通過“资金流入流出预测”大赛在线评测系统进行评测。通过与简单ARMAGARCH、GMAR模型和GMSARIMA模型进行对比，结果显示，本文建立模型的平均绝对误差（MAE）和平均绝对百分比误差（MAPE）均为最小，且误差小于10%的精确预测点数也最多，仅部分点的预测精度稍差，总体结果良好。

1数据来源与预处理

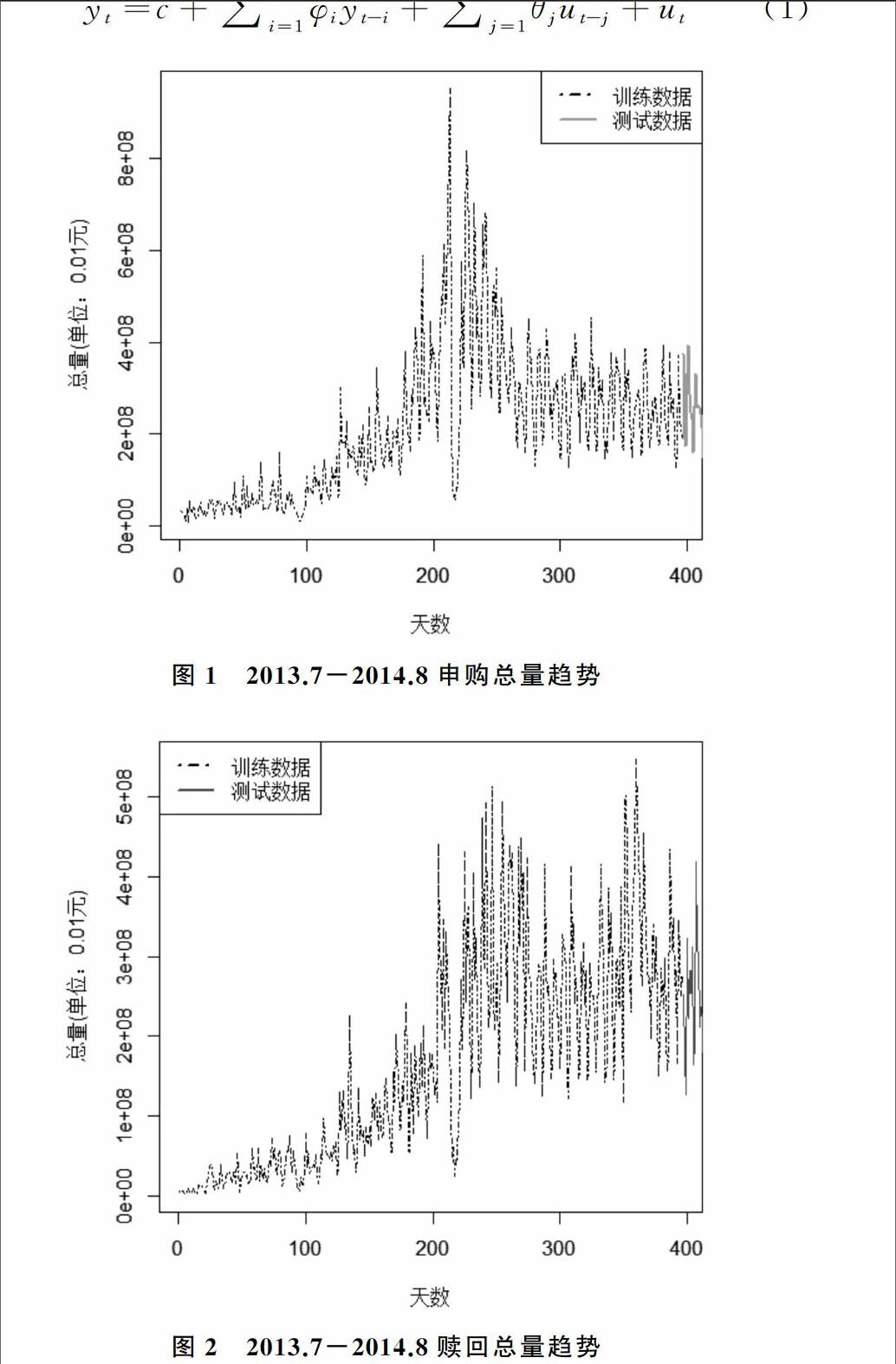
本文数据来源于蚂蚁金服提供的“资金流输入输出预测”大赛数据，该数据为3万用户在2013年7月1日～2014年8月31日期间每天的投资记录。数据主要字段包括用户id、日期、今日总申购量、今日总赎回量等。对货币基金而言，资金流入意味着申购行为，资金流出为赎回行为。将资金输入曲线称为申购曲线，资金流出曲线称为赎回曲线。2013年7月1日～2014年8月31日共427天，接着按天进行分组，计算每天的申购总量和赎回总量。选择2013年7月1日～2014年7月31日期间共396天的数据为训练集，2014年8月共31天的数据为测试集，使用ARMAGARCH模型进行预测，并与SARIMA模型、AR模型、GMAR模型以及GMSARIMA模型进行对比分析。申购总量和赎回总量曲线如图1所示。

图1中，申购总量先快速增长，接着又逐渐下降，最后波动趋于稳定，申购总量最大值为952 479 658，最小值为8 962 232。图2中，赎回总量刚开始也同样快速增长，但其随后就处于趋势不稳定的波动中，赎回总量最大值为547 295 931，最小值为1 616 635。

2本文方法

通过分析资金流的特点，首先通过差分方法将资金流转换成增益序列，然后结合ARMA模型和GARCH模型，构建了ARMAGARCH模型，对增益序列进行建模。

ARMA模型又称为自回归移动平滑模型，由自回归模型（简称AR模型）与滑动平均模型（简称MA模型）为基础“混合”构成。ARMA（p，q）模型中包含了p自回归项和q移动平均项，ARMA（p，q）模型可以表示为：yt=c+∑pi=1φiyt-i+∑qj=1θjut-j+ut（1）图12013.7-2014.8申购总量趋势图22013.7-2014.8赎回总量趋势GARCH模型称为广义ARCH模型，是ARCH模型的拓展，是由Bollerslev发展而来。GARCH模型是一个专门针对金融数据量体订做的回归模型，除了和普通回归模型的相同之处外，GARCH对误差的方差进行了进一步建模，特别适用于波动性的分析和预测。GARCH模型的一般表达式含有r个ARCH项和s个GARCH项：rt=c1+∑pi=1irt-i+ut（2）

δ2t=α0+∑ri=1αiμ2t-i+∑sj=1βjδ2t-j（3）其中δ2t为条件方差，μt为独立分布的随机变量 ，式（2）称为条件均值方程，由ARMA（p，q）模型表示；式（3）称为条件方差方程，说明时间序列条件方差的變化特征。

ARMAGARCH 模型是分别对均值和方差建模，即均值满足ARMA过程，残差满足GARCH过程的一个随机过程，其方程如下：yt=c+∑pi=1φiyt-i+∑qj=1θjut-j+ut（4）

δ2t=α0+∑ri=1αiu2t-i+∑sj=1βjδ2t-j（5）其中，δ2t是条件方差，ut=δtεt，且φi，θj，α0，αi，βj（ i=1，…，p；j=1，…，q）为待估参数。式（4）称为条件均值方程，由ARMA（p，q）模型表示。式（5）称为条件方差方程，由GARCH（r，s）模型表示。

GARCH模型中误差分布一般有3种假设：①正态分布；②t分布；③GED分布。有学者建立ARMAGARCH模型对2004年9月30日～2011年9月30日期间的上证指数收盘价进行拟合和预测，使用正态分布、t分布和GED分布进行对比，实验显示，t分布的ARMAGARCH模型最优[17]。因此，在本文中采用t分布作为误差分布。

3实验过程及结果分析

3.1模型参数选择

通过对数据的分析选择合适的ARMA（p，q）-GARCH（r，s）模型参数，主要分为3步：

（1）通过差分计算申购和赎回曲线的增益序列，并对样本的增益序列进行基本统计分析。

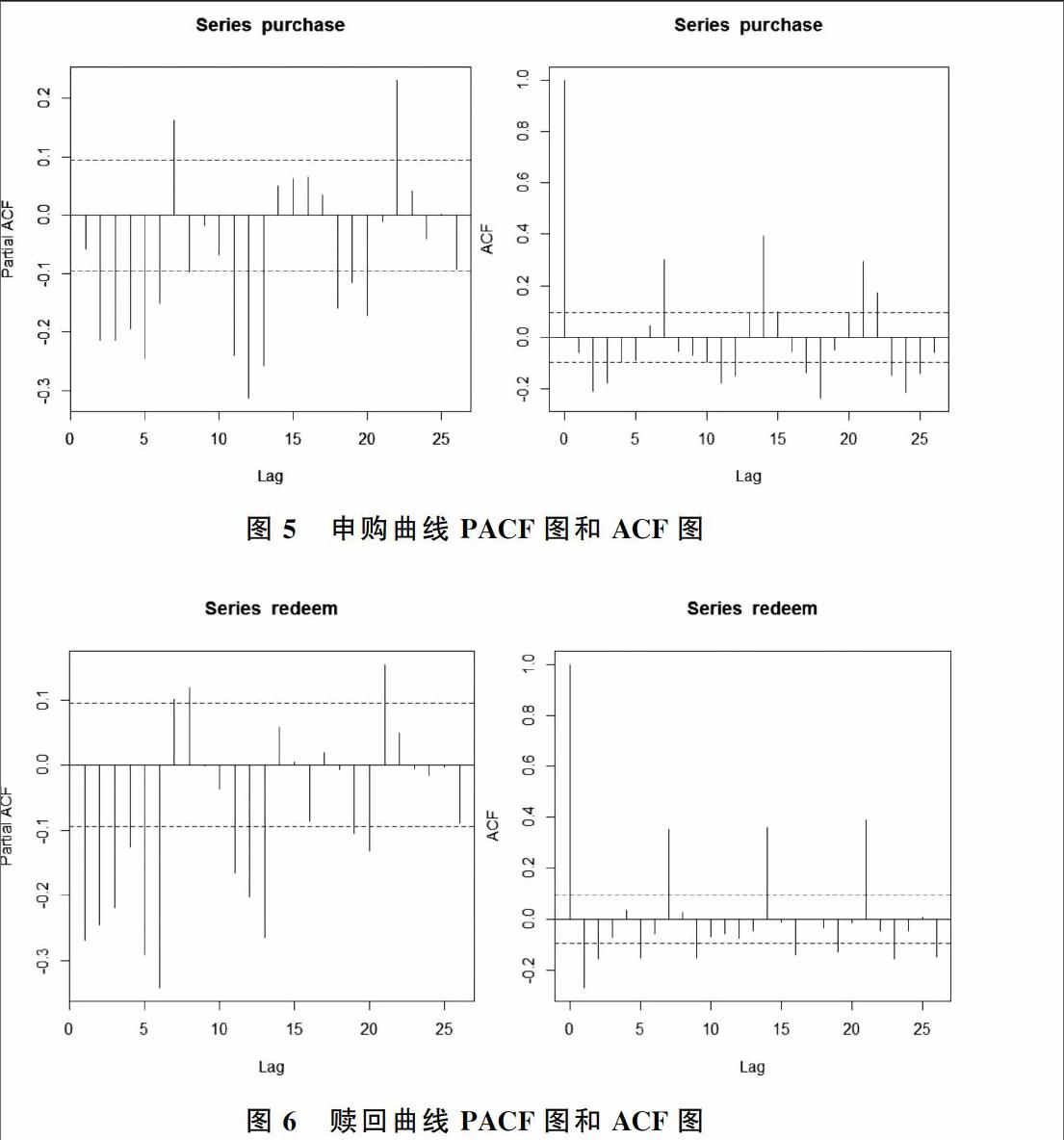
8赎回增益曲线（2） 检测申购曲线和赎回曲线增益序列的相关性。通过分析增益序列相应的偏自相关函数（PACF）图和自相关函数（ACF）图，发现PACF图和ACF图都是拖尾的，因此设定为ARMA过程。接着，根据PACF和ACF的显著性，确定ARMA（p，q）模型中p和q的阶数，如图5、图6所示。

同理，在赎回曲线的ARMA（p，q）模型中，p根据图6左图中的PACF图选为8，q根据右图中的ACF图选为2，即构建了ARMA（8，2）模型。

（3）选择条件方差方程。GARCH（1，1）模型要求的参数较少，适用于估计或预测金融时间序列数据的波动性和相关性。苏岩等[18]曾利用ARMA模型、GARCH（1，1）模型、EGARCH模型等检验人民币/日元汇率波动，结果显示GARCH（1，1）拟合效果最好，且预测效果与实际情况一致。本文选择GARCH（1，1）作为ARMAGARCH模型的条件方差方程，误差分布选用t分布。

根据以上数据分析结果，最终得到两个模型：ARMA（7，5）-GARCH（1，1）申购预测模型和ARMA（8，2）-GARCH（1，1）赎回预测模型，下面将使用这两个模型进行预测。

3.2预测及结果分析

使用以上得到的ARMA（7，5）-GARCH（1，1）预测模型和ARMA（8，2）-GARCH（1，1）预测模型分别对2014年8月的申购和赎回数据进行预测，并与简单ARMAGARCH、GM

本文方法和简单ARMAGARCH模型对波动性小的点预测效果好，而对第9、17、23、24天等波动性较大的点预测效果差；GMSARIMA模型对波动性较大的点预测效果好，由于受波动点的影响，对点的预测精度不高；GMAR模型对点的预测精度差，整体预测趋势与曲线相似。由图8可知，各个模型的预测效果明显较差。

下面通过平均绝对误差MAE和平均绝对百分比误差MAPE对各种模型的预测情况进行对比。考虑金融行业数据分析的特点，引入误差小于10%的点数作为标价指标，进一步对以上结果进行对比分析。

MAE和MAPE计算公式如下：MAE=1n∑ni=1fi-yi=1n∑ni=1ci（6）

MAPE=1n∑ni=1fi-yiyi×100=1n∑ni=1ciyi×100（7）其中，fi为预测值，yi为真实值，ci=fi-yi为绝对误差。

4结语

本文根据资金流特点，通过差分处理将资金流转换成增益序列，然后引入ARMAGARCH模型对其进行分析。在对资金流时间序列申购和赎回数据进行预测时，发现对增益序列构建的ARMAGARCH模型较简单，ARMAGARCH模型误差更小且精度更高，同时较GMAR模型和GMSARIMA模型有更小的预测误差和更高的预测精度，其平均绝对误差MAE和平均绝对百分比误差MAPE都是最小的，且预测误差小于10%的准确点数也是最多的。然而，实验中发现本文方法对一些变化频率较大序列段的分析效果不佳，导致最终误差较大。对部分点的预测误差较大等原因，后续将进一步研究改进。

参考文献：

[1]齐立新，贾云龙，唐海川.基于AR模型的海洋环境噪声仿真预测研究[J].海洋技术学报，2010（2）：6062.

[2]谭巧巧，杨吉云.改进的自回归AR（p）预测模型在WSN中的应用[J].计算机工程与应用，2015（12）：8387.

[3]王志坚，王斌会.基于ARMA模型的社会消费品零售总额预测[J].统计与决策，2014（11）：7779.

[4]许凤华，魏媛.ARMA模型在小麦价格指数预测中的应用[J].统计与决策，2015（8）：8284.